復雜電網自組織臨界態辨識物理指標研究

劉文穎 但揚清 朱艷偉 梁 才 蔡萬通 王維洲 鄭 偉

（1.華北電力大學電氣與電子工程學院 北京 102206 2.國網浙江省電力公司寧波供電公司 寧波 315010 3.國網甘肅省電力公司電力科學研究院 蘭州 730050）

1 引言

近年來對連鎖故障的歷史數據研究[1-3]表明，連鎖故障的發生服從冪律或冪律尾分布，而非指數分布，此時系統發生大負荷損失故障的概率是不可忽略的。也即表明電網是一復雜系統，其連鎖故障的發生表現出復雜系統特性——自組織臨界特性。為了避免歷史數據的局限性，研究人員設計出了基于直流潮流、考慮隱性故障和基于交流潮流等連鎖故障模型[4-9]，為進一步研究電網自組織臨界特性的影響因素和行為特征提供了有效途徑。從傳統角度出發，線路潮流的平均負載率是影響電力網絡連鎖故障傳播和是否進入自組織臨界態的重要因素之一。但在系統平均負載率低時，不能排除系統進入自組織臨界態的可能性。文獻[10]對我國華北電網2005 年夏大方式下的運行數據進行了分析，發現該電網在平均負載率僅為0.278 時便進入了自組織臨界態。因而僅根據平均負載率的大小來判斷電網是否進入自組織臨界態是欠妥的。文獻[11]提出電網結構的不均衡性導致了電網自組織臨界特性的出現，在相同的負荷水平和線路潮流分布情況下，電網結構越不均勻，系統越容易趨向自組織臨界態。文獻[12]研究了潮流的不均衡性對電網連鎖故障和自組織臨界特性的影響，認為潮流的不均衡性導致了電網自組織臨界態的出現。文獻[13]研究了負載率分布對電網連鎖故障和自組織臨界特性的影響，實際上潮流熵就是負載率分布的一種體現，其分析結論與文獻[12]結論是一致。潮流分布的不均衡性存在以下兩種情況:由于部分線路負載率偏低而致的潮流不均衡性和由于部分線路負載率偏高而致的潮流不均衡性，顯然后者是系統是否進入自組織臨界態的決定性因素。而潮流熵概念對上述兩種潮流不均衡性不能加以很好的區分。基于此，本文提出以加權潮流熵來刻畫潮流分布的不均衡性，該物理指標配以網絡拓撲熵能夠更加全面地表征電網自組織臨界特性。

2 復雜電網自組織臨界特性物理指標的提出

2.1 復雜電網的自組織臨界特性

電網連鎖故障引發的大停電事故是系統處于自組織臨界狀態時，在微小的擾動下觸發連鎖反應并導致災變的過程現象[2]。電網由安全穩定運行狀態趨向自組織臨界態的演化過程是在電網負荷不斷增長和網絡不斷改善兩種相反的作用力相互作用下完成的[14,15]。

網絡結構在電網規劃和電網改造期內，具有穩定不變性。隨著社會經濟的發展，負荷會不斷增長。致使部分關鍵輸電斷面上的線路出現負載率飆升，而與發電機相連的線路負載率基本保持不變，潮流分布趨向不均衡。此時發生連鎖故障的風險顯著增加。新一輪電網規劃或電網改造完成后，網絡結構依據負荷和電源分布進一步合理化布局，電網的負荷壓力得到一定程度的緩解。如高一級電壓等級電網的建設，伴隨著少量低電壓等級線路的退出運行，使得網絡結構的度分布趨向均勻化；同時高一電壓等級的輸電能力較原電壓等級有顯著提升，相關線路負載率會大幅下降，潮流分布亦趨向均衡化，此時電網安全性能較高。

然而，由于實際電網規劃與改造進度難以實時跟蹤負荷的增長，使得實際電力系統在負荷日益增長和電網日益加強兩種方向相反的作用力下，自然地朝著臨界態演化。電力系統一旦進入自組織臨界態后，系統將會變得異常脆弱，易發生規模大小不一的連鎖反應故障。這種特性在數學上表征為負荷損失量累積分布滿足冪律關系:

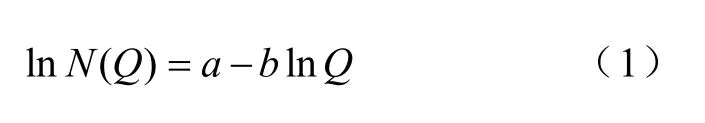
式中，a、b為常數。在雙對數坐標系下，負荷損失量與大于該負荷損失量對應的事故發生概率曲線在尾部近似為一條直線。圖1 給出了美國大停電損失的負荷和發生概率的冪律關系[4]，這種關系被認為是電網自組織臨界特性的數學表征。

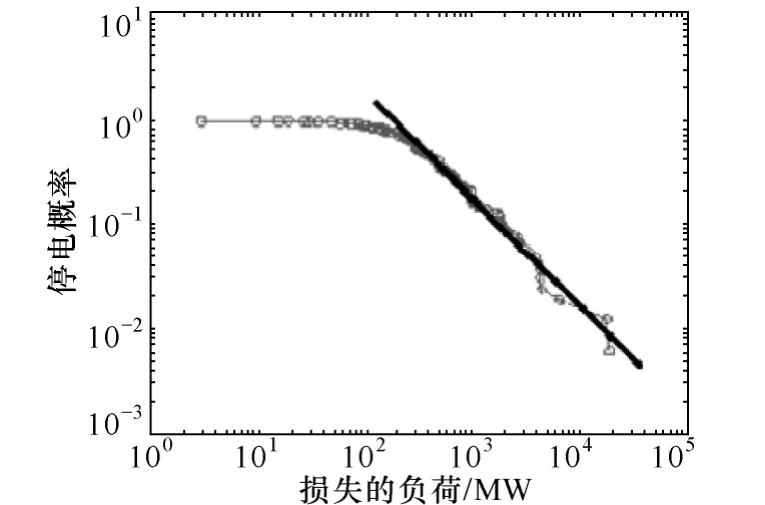
圖1 大停電損失的負荷與停電概率的冪律關系Fig.1 Power law relation between lost load and probability of blackout

因而在研究電網的自組織臨界特性時，負荷增長和網絡改善因素至關重要。

2.2 復雜電網自組織臨界態辨識物理指標

復雜電網處于自組織臨界態時，在物理行為上表征為網絡拓撲結構和潮流的高度不均衡性，可以采用網絡拓撲熵和加權潮流熵來刻畫。

2.2.1 網絡拓撲熵

網絡拓撲熵是網絡的一種無序的度量，表征了網絡中節點的重要度分布[16]。

設一網絡有n個節點，其中節點i的度為ki，定義該節點重要度Ii為

它滿足條件

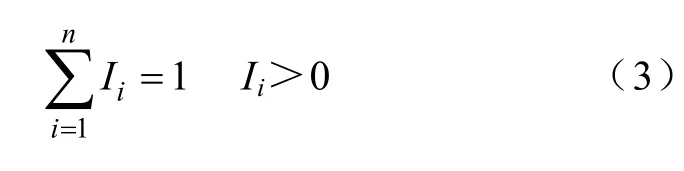
根據香農（C.E.Shannon）定理對熵的定義，給出網絡拓撲熵[11]HN

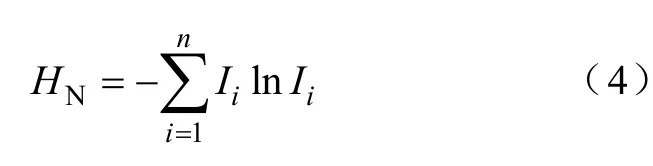
求取最大網絡拓撲熵[17]即為，在式（3）約束條件下，求取式（4）的極值問題。應用拉格朗日乘數法容易求得極大值點:

即Ii=1/n時，網絡拓撲熵取得最大值HNmax=lnn，此時網絡節點邊連接完全均勻。

相反的情況是當網絡中所有節點都與某一個中樞節點相連時，網絡最不均勻，網絡拓撲熵最小。

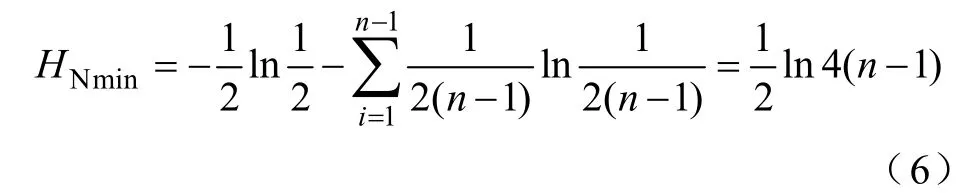
2.2.2 加權潮流熵

潮流熵刻畫的是負載率在各個負載率區間(ku,(k+1)u)（k=0,1,2,···）上的分布情況，而潮流分布的不均衡性存在由部分線路負載率偏低而致和由部分線路負載率偏高而致的兩種情況。顯而易見，存在部分線路負載率偏高的潮流分布不均衡性是電網自組織臨界特性的決定性因素，而由于部分負載率偏低所致的潮流分布不均衡性誘發連鎖故障的概率則會低得多。因而以區間平均負載率作為權值的加權潮流熵概念來刻畫潮流的不均衡性更加合理。

設線路i的最大傳輸容量為，系統運行時線路i實際潮流為，則線路i的負載率為

式中，Nl為線路數。

給定常數序列U=[0,u,2u,…,ku，(k+1)u,…,nu],nu=100%，對于過載線路負載率不再細分，均置于(nu,(n+1)u)區間。用lk表示負載率μi∈（ku，(k+1)u］(k=0,1,2,n) 的線路條數，則線路負載率處于(ku,(k+1)u) 區間的概率p(k)為

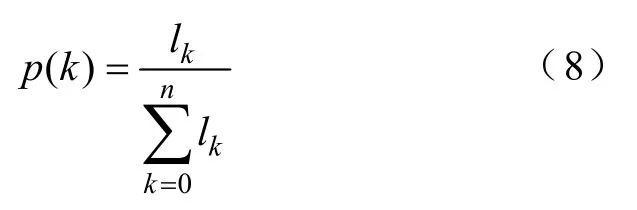
由熵定義與式（8）得電力網絡潮流熵HP為

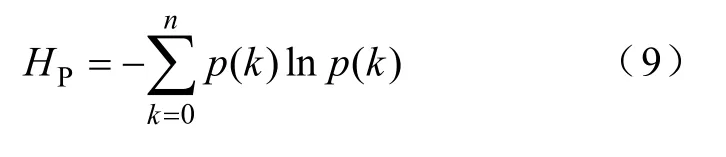
在式（9）潮流熵[18]定義的基礎上，以處于(ku,(k+1)u) 區間內所有線路負載率的平均值作為該區間熵值的權值，定義加權潮流熵HPw為

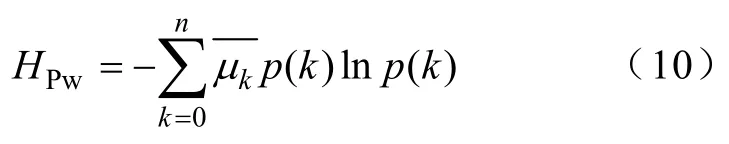
若(ku,(k+1)u]區間內有m條線路，則

設某區域電網在安全穩定運行狀態（正常狀態）和高危運行狀態下的潮流分布見表1，線路總條數為100 條，負載率等分為n=20個區間，u=5%。

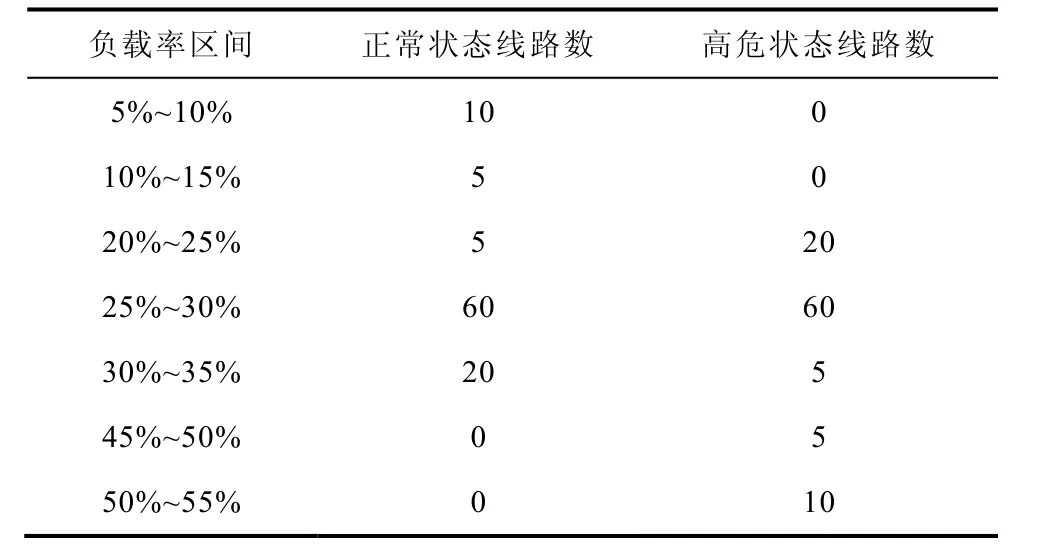
表1 兩種狀態下的潮流分布Tab.1 Power flow distribution of two states

分別按照式（9）和式（10）計算兩種狀態下的潮流分布指標見表2。

表2 兩種狀態下的潮流分布指標對照表Tab.2 Power flow distribution indicators of two states

由表2 可知，兩種狀態下的平均負載率和潮流熵均相同，即認為潮流的不均衡度相同，具有相同的自組織臨界特性。然而實際上，由表1 可知，正常狀態的潮流不均衡性是由于部分線路負載率處于5%～10%和10%～15%兩個低負載率區間而導致的；高危狀態的潮流不均衡性是由于部分線路負載率處于45%～50%和50%～55%兩個高負載率區間而導致的。顯然高危狀態比正常狀態發生連鎖故障的風險大。換句話說，平均負載率和潮流熵概念無法對正常狀態和高危狀態兩種完全不同的狀態進行區分；而在高危狀態下的加權潮流熵大于正常狀態的加權潮流熵表征了高危狀態比正常狀態下發生連鎖故障的風險大這一特征。

3 電網自組織臨界態辨識物理指標仿真分析

研究表明，電力系統連鎖故障的主要原因是有功潮流的大規模轉移及支路過載效應[19,20]。因而本文采用文獻[9]建立的OPA 模型快速動態過程作為連鎖故障的仿真模型。以甘肅電網2008 年冬大、2010 年冬大和2012 年冬大三個運行方式典型運行數據進行仿真計算，分析網絡拓撲熵和加權潮流熵對電網自組織臨界特性的影響，驗證電網處于自組織臨界態時，在物理上表征為低網絡拓撲熵和高加權潮流熵這一特性。

甘肅電網 2008 年冬大典型運行方式下，以330kV 電網為主網架，750kV 線路僅有蘭（甘蘭州東）-平（甘平涼）-乾（陜乾縣）雙回投入運行，相對比較單薄，如圖2 所示。

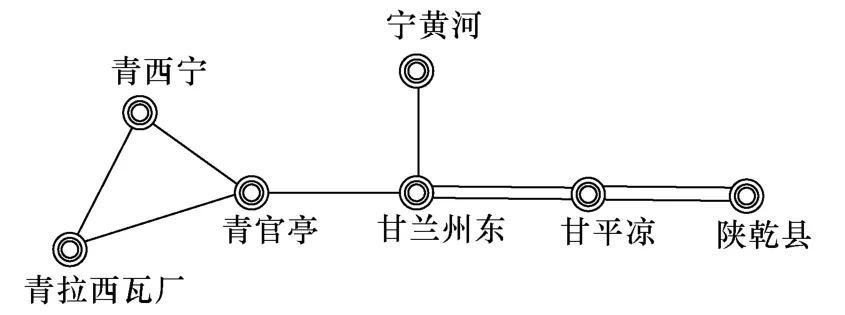
圖2 2008 年甘肅750kV 網架Fig.2 Gansu 750kV grid structure in 2008

2010 年冬大典型運行方式下甘肅電網 750kV線路已初步形成如圖3 所示的網絡，電網得到了一定加強。

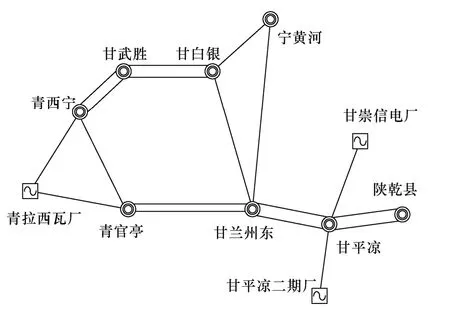
圖3 2010 年甘肅750kV 網架Fig.3 Gansu 750kV grid structure in 2010

2012 年冬大方式下，750kV 網絡得到進一步完善，特別是750kV 雙回線武勝（甘武勝）=河西（干河西）=酒泉（甘酒泉）=敦煌（甘敦煌）=哈密的投運，打通了河西風電富裕電量外送通道，使得河西電網網絡結構趨于合理化。外送通道如圖4 所示。即從主網架看，08 年冬大、10 年冬大、12 年冬大三個典型運行方式下的網絡結構得到了不斷加強。

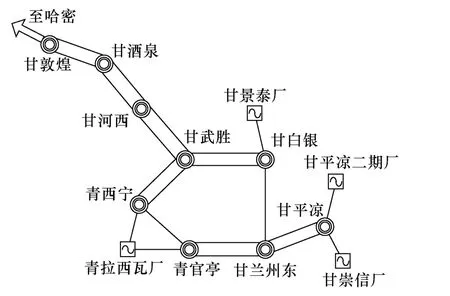
圖4 2012 年甘肅750kV 網架Fig.4 Gansu 750kV grid structure in 2012

3.1 在加權潮流熵不變的情況下，網絡拓撲熵對自組織臨界態的影響

假設負荷水平不變，維持在2012 年冬大負荷方式下。將2012 年冬大負荷分別與2008 年和2010年冬大典型運行方式網架整合，形成兩個新的運行方式，以仿真甘肅電網自組織臨界特性隨網絡結構變化的演化過程。

通過調整開機方式，將潮流調至合理范圍，同時確保三個運行方式下的加權潮流熵一致。通過式（4）計算，得到該三種方式下的網絡拓撲熵見表3。表3 中運行方式命名方法采用網絡結構加負荷名方式，如08Net-08Load 表示該運行方式為08 年冬大典型運行方式，08Net-10Load 表示該方式是將10年冬大典型運行方式的負荷與08 年冬大典型運行方式網架整合后的運行方式。

表3 三種運行方式下的網絡拓撲熵加權潮流熵Tab.3 Network topology entropy and weighted power flow entropy of three operation modes

從表3 中可以看出，08 年冬大、10 年冬大、12年冬大三個典型運行方式下，隨著網絡結構的加強，其網絡拓撲熵逐步遞增。

對該三個典型方式分別進行200 次連鎖故障仿真，每次隨機選取1 條線路斷開，得到連鎖故障發生頻次和負荷損失情況見表4。

表4 三種運行方式下連鎖故障發生頻次和總負荷損失量Tab.4 Cascading failure frequency and total load loss of three operation modes

由表4 可知，隨著網絡結構的加強，連鎖故障發生頻次和總負荷損失量均明顯下降。圖5 給出了負荷損失量的累積分布特征，橫坐標表示負荷損失量（表征連鎖故障的規模），縱坐標表示大于某一負荷損失量的連鎖故障發生的概率，橫、縱坐標均為對數坐標。

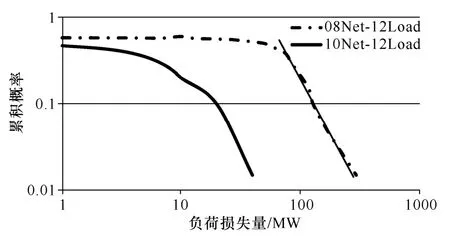
圖5 不同網絡結構下負荷損失量的分布特性Fig.5 Distribution of load loss with variant structures

如圖5 所示，在2012 年冬大典型方式（HN=5.556）下，沒有任何規模的負荷損失事故發生，說明此時電網遠離自組織臨界態，電網處于安全穩定運行狀態。而將2012 年負荷量整合至2008 年和2010 年網架之上后，則均有負荷損失事故發生。2010 年網架（HN=5.402）下，發生大停電事故的風險較小，僅存在局部脆弱地區可能會發生小規模負荷損失事故，此時電網正朝著自組織臨界態演化。2008 年網架（HN=5.162）下發生大規模停電事故的概率則明顯高于2010 年網架方式，負荷損失量的累積概率分布呈現出明顯的冪律尾特征，可以認為此時電網處于自組織臨界態。此時任一微小的干擾均有可能導致大規模的連鎖反應，出現大停電事故。

因而，在加權潮流熵不變的情況下，隨著網絡拓撲熵的減小，電網發生大負荷損失事故的風險明顯上升，朝著自組織臨界態方向演化。

3.2 在網絡結構熵不變的情況下，加權潮流熵對自組織臨界態的影響

現假設甘肅電網網絡結構維持在2008 水平年，負荷和省際斷面交換功率從2008 年至2012 年逐步演變，以改變加權潮流熵，仿真電力系統的自組織臨界特性演化過程。

按照負荷比例將2010 年和2012 年冬大方式下的負荷量整合至2008 年冬大方式網絡結構之上，調整開機方式，將潮流調至合理范圍。計算這三種典型運行方式下的加權潮流熵見表5。

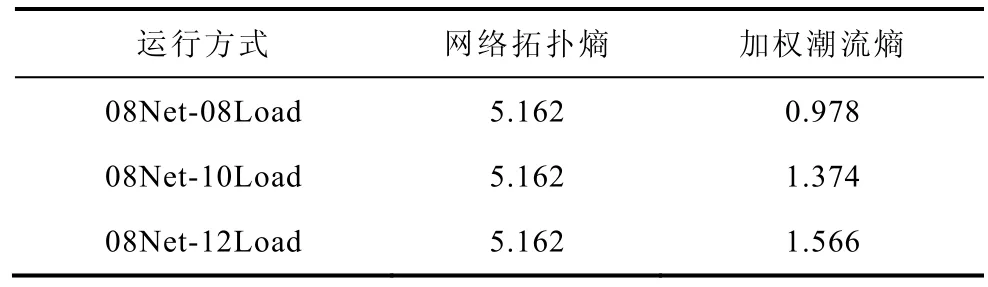
表5 三種運行方式下的網絡拓撲熵和加權潮流熵Tab.5 Network topology entropy and weighted power flow entropy of three operation modes

對該三個典型方式分別進行200 次連鎖故障仿真，每次隨機選取1 條線路斷開，得到連鎖故障發生頻次和負荷損失情況見表6。

從表5 和圖6 中可以看出，隨著負荷的增長，加權潮流熵增大，連鎖故障發生頻次與總負荷損失量均大幅增大。圖6 給出了負荷損失量的累積分布特性。

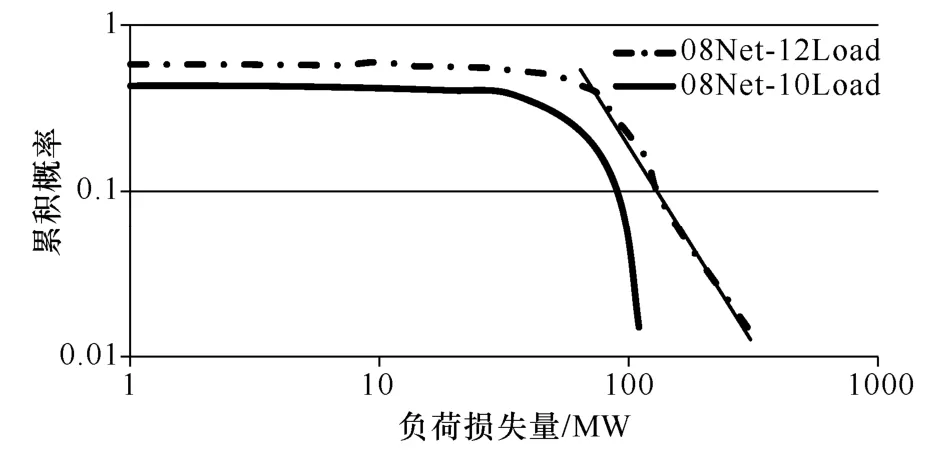
圖6 不同負荷水平下負荷損失量的分布特性Fig.6 Distribution of load loss with variant loads

如圖6 所示，在2008 年冬大典型方式（HPw=0.978）下，沒有任何規模的停電事故發生，說明此時電網遠離自組織臨界態，電網能夠安全穩定的運行。2010 年負荷整合至2008 年網架（HPw=1.374）之上后，出現一些小負荷損失事故，發生大負荷損失事故的概率則很小，此時電網向自組織臨界態方向演化。而 2012 年負荷整合至 2008 年網架上（HPw=1.566）之后，負荷損失量的累積概率分布特性呈現出明顯的冪律尾特性，發生大停電的連鎖故障風險迅速上升。可以認為此時系統已進入自組織臨界態，任一微小的擾動均有可能導致大規模的停電事故發生。

因而，在網絡結構不變的情況下，隨著加權潮流熵的增加，電網發生連鎖故障的風險上升，電網朝著自組織臨界態演化。

3.3 潮流熵與加權潮流熵

表7 列出了同一網絡結構下的三個典型運行方式的潮流熵和加權潮流熵對照表。

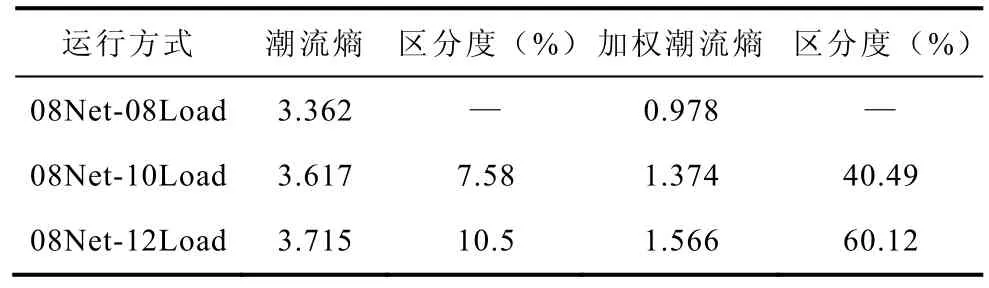
表7 潮流熵與加權潮流熵對比Tab.7 Comparison between weighted power flow entropy and power flow entropy

表7 中的區分度是以08Net-08Load 安全穩定運行狀態為基礎，其他方式下（加權）潮流熵對其指標差值的百分數，以衡量系統離開安全穩定運行狀態的距離。將2010 年和2012 年冬大負荷整合至2008 年的網架上，致使系統負載率普遍有所上升。特別是關鍵輸電通道和斷面上負載率居高，致使潮流分布愈加不均勻，已遠離安全穩定運行狀態。然而，由表7 可知，從潮流熵的角度看，08Net-10Load和08Net-12Load 對08Net-08Load 的區分度均很小，無法很好地表征08Net-10Load 和08Net-12Load 兩種方式下的由于部分線路負載率偏高而致的潮流不均衡性。而從加權潮流熵的角度看，08Net-10Load 和08Net-12Load 對08Net-08Load 的區分度超過40%，顯著地表征了08Net-10Load 和08Net-12Load 兩種方式下的由于部分線路負載率偏高而致的潮流不均衡性和該狀態已遠離安全穩定運行狀態這一信息。

4 結論

網絡結構和潮流分布的高度不均衡性是電網是否進入自組織臨界態的決定性因素。網絡結構的不均衡性一般采用網絡拓撲熵來刻畫。對于潮流的不均衡性問題，本文針對潮流熵概念無法區分由于部分線路負載率偏低而致的不均衡性和由于部分線路負載率偏高而致的不均衡性兩種不同狀態的問題，提出采用加權潮流熵概念刻畫潮流的不均衡性。通過對實際電網的實例仿真得到以下結論:

（1）在加權潮流熵不變的情況下，隨著網絡拓撲熵的減小，電網發生連鎖故障的風險上升，電網朝著自組織臨界態方向演化。

（2）在網絡拓撲熵不變的情況下，隨著加權潮流熵的增加，電網發生連鎖故障的風險上升，電網朝著自組織臨界態方向演化。

（3）與潮流熵相比，加權潮流熵能夠很好地區分出由于部分線路負載率偏低而致和由于部分線路負載率偏高而致的兩種潮流分布不均衡性。

因此，網絡拓撲熵和加權潮流熵可作為電網自組織臨界態辨識的兩個關鍵指標。根據網絡拓撲熵和加權潮流熵等物理指標進行電網自組織臨界態的辨識具有重要的現實意義。如何利用這兩個指標進行復雜電網自組織臨界態的辨識和評估有待下一步進行深入研究。

[1]Carreras B A,Newman D E,Dobson I,et al.Evidence forself-organized criticality in electric power system blackouts[C].Hawaii International Conference on System Sciences,Hawaii,2001:705-709.

[2]曹一家,江全元,丁理杰.電力系統大停電的自組織臨界現象[J].電網技術,2005,29(15):1-5.Cao Yijia,Jiang Quanyuan,Ding Lijie.Self-organized criticality phenomenon for power system blackouts[J].Power System Technology,2005,29(15):1-5.

[3]于群,郭劍波.中國電網停電事故統計與自組織臨界特性特征[J].電力系統自動化,2006,30(2):16-21.Yu Qun,Guo Jianbo.Statistics and self-organized criticality characters of blackouts in China electric power systems[J].Automation of Electric Power Systems,2006,30(2):16-21.

[4]Dobson I,Carreras B A,Lynch V E,et al.An initial model for complex dynamics in electric power system blackouts[C].Proceedings of the 34th Hawaii International Conference on System Sciences,Maui,Hawaii,2001,2:710-718.

[5]鄭陽,劉文穎,溫志偉,等.基于小世界網絡的電網連鎖故障實時搜索系統[J].電網技術,2010,34(7):58-63.Zheng Yang,Liu Wenying,Wen Zhiwei,et al.A real-time searching system for cascading failures of power grids based on small-world network[J].Power System Technology,2010,34(7):58-63.

[6]王英英,羅毅,涂光瑜,等.電力系統連鎖故障的關聯模型[J].電工技術學報,2012,27(2):204-209.Wang Yingying,Luo Yi,Tu Guangyu.Correlation model of cascading failures in power system[J].Transaction of China Eletrotechnical Society,2012,27(2):204-209.

[7]易俊,周孝信.考慮系統頻率特性以及保護隱藏故障的電網連鎖故障模型[J].電力系統自動化,2006,30(14):1-5.Yi Jun,Zhou Xiaoxin.A cascading failure model of power system considering frequency response characteristics and hidden failures[J].Automation of Electric Power Systems,2006,30(14):1-5.

[8]曹一家,丁理杰,等,考慮網絡演化的直流潮流停電模型與自組織臨界特性分析[J].電力系統自動化,2009,33(5):1-6.Cao Yijia,Ding Lijie,et al.Analysis on cascading failure and self-organized criticality in evolving power grids[J].Automation of Electric Power Systems,2009,33(5):1-6.

[9]梅生偉,何飛,張雪敏,等.一種改進的OPA 模型及大停電風險評估[J].電力系統自動化,2008,32(13):1-5.Mei Shengwei,He Fei,Zhang Xuemin,et al.An improved OPA model and the evaluation of blackout risk[J].Automation of Electric Power Systems,2008,32(13):1-5.

[10]周孝信,肖逾男.用連鎖故障搜索算法判別系統的自組織臨界狀態[J].中國電機工程學報,2007,27(25):1-5.Zhou Xiaoxin,Xiao Yunan.Determining the selforganized criticality state of power systems by the cascading failures searching method[J].Proceedings of the CSEE,2007,27(25):1-5.

[11]梁才,劉文穎,溫志偉,等.電網組織結構對其自組織臨界特性的影響[J].電力系統保護與控制,2010,38(20):6-11.Liang Cai,Liu Wenying,Wen Zhiwei,et al.The influences of power grid structure on self-organized criticality[J].Power System Protection and Control,2010,38(20):6-11.

[12]曹一家,王光增,曹麗華,等,基于潮流熵的復雜電網自組織臨界態判斷模型[J].電力系統自動化,2011,35(7):1-6.Cao Yijia,Wang Guangzeng,Cao Lihua,et al.An identification model for self-organized criticality of power grids based power flow entropy[J].Automation of Electric Power Systems,2011,35(7):1-6.

[13]于群,曹娜,郭劍波.負載率對電力系統自組織臨界狀態的影響分析[J].電力系統自動化,2012,36(1):24-27,37.Yu Qun,Cao Na,Guo Jianbo.Analysis on influence of load rate on power system self-orgnized criticality[J].Automation of Electric Power Systems,2012,36(1):24-27,37.

[14]陳曉剛,孫可,曹一家.基于復雜網絡理論的大電網結構脆弱性分析[J].電工技術學報,2007,22(10):138-144.Chen Xiaogang,Sun Ke,Cao Yijia.Structural vulnerability analysis of large power grid based on complex network theory[J].Transaction of China Eletrotechnical Society,2007,22(10):138-144.

[15]曹一家,陳彥如,曹麗華,等.復雜系統理論在電力系統中的應用研究展望[J].中國電機工程學報,2012,32(19):1-9.Cao Yijia,Chen Yanru,Cao Lihua,et al.Prospects of studies on application of complex system theory in power systems[J].Proceedings of the CSEE,2012,32(19):1-9.

[16]Wang J W,Rong L L.Cascade-based attack vulnerability on the US power grid[J].Safety Science,2009,47(10):l332-l336.

[17]楊建民,張寧.復雜網絡演化的自組織現象[J].上海理工大學學報,2005,27(5):413-416.Yang Jianmin,Zhang Ning.Self-organization phenomena of complex network evolution[J].Journal of University of Shanghai for Science and Technology,2005,27(5):413-416.

[18]Bao Z J,Cao Y J,Wang G Z,et a1.Analysis of cascading failure in electric grid based on power flow entropy[J].Physics Letters A,2009,373(34):3032-3040.

[19]曹一家,張宇棟,林輝,等.基于同配性的電力系統自組織臨界性識別[J].電力系統自動化設備,2013,33(7):6-11,18.Cao Yijia,Zhang Yudong,Lin Hui,et al.Power system self-organized criticality recognition based on assortativity[J].Electric Power Automation Equipment,2013,33(7):6-11,18.

[20]李蓉蓉,張曄,江全元.復雜電力系統連鎖故障的風險評估[J].電網技術,2006,30(10):18-23.Li Rongrong,Zhang Ye,Jiang Quanyuan.Risk assessment for cascading failures of complex power system[J].Power System Technology,2006,30(10):18-23.