三相四橋臂PWM 整流器的研究

韋 徵 陳 新 陳 杰 李臣松 龔春英

（南京航空航天大學自動化學院 南京 210016）

1 引言

三相電壓型PWM 整流器廣泛應用在人們的生產生活中，改善整流器的性能，減小輸入電流諧波含量，提高系統的功率因數具有重要意義。在3P3W（three-phase three-wire）系統中，傳統的大功率整流器多用三相三橋臂電壓型PWM 整流器拓撲，其拓撲結構簡潔，能實現功率的雙向流動，對它經過電壓電流雙閉環控制可實現三相輸入的高功率因數校正[1-8]。

除了3P3W 系統之外，很多應用場合出于防雷、絕緣、中線電流補償等考慮，需要采用 3P4W（three-phase four-wire）的連接方式。如并聯有源電力濾波器、動態電壓恢復器、不間斷電源等[9]。目前常見的3P4W 系統拓撲分為三橋臂-分裂電容拓撲以及四橋臂-全橋拓撲，其主電路分別如圖1a和圖1b 所示。在三橋臂-分裂電容拓撲中，中間直流電容中點O 與三相Y 形聯結的輸入電源的中點N相連，該電路拓撲的優點為開關數量少，電流控制相對簡單。同時由于分裂電容的存在，在控制中需要考慮分裂電容均壓問題，增加電容均壓環節，故在一定程度上又增加了控制的復雜性。相比3P3W系統，三橋臂-分裂電容拓撲輸入橋臂電壓只能在兩個電平（-Udc/2,Udc/2）間跳變，諧波抑制的效果低于3P3W 系統，從而輸入電流波形的畸變度也較高[10]。

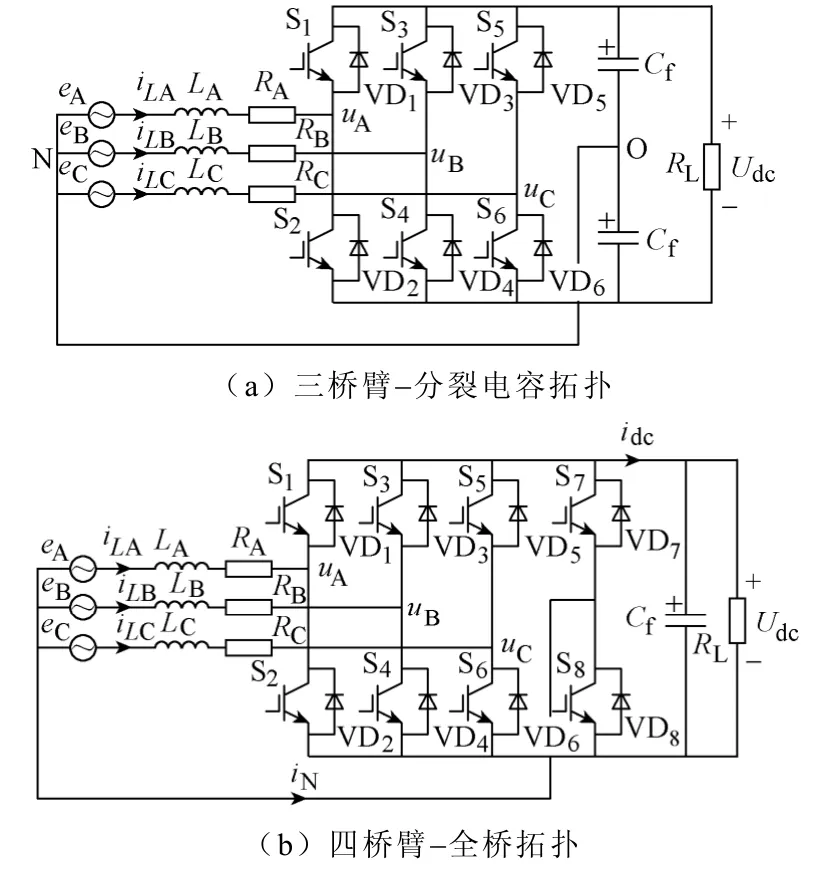
圖1 3P4W 系統拓撲Fig.1 Circuit diagram of 3P4W system

對于四橋臂-全橋拓撲，由于增加了一個橋臂，對于電路結構而言，增加了其復雜性，但是在控制上，橋臂的增加使得對電路的控制更為靈活。特別是當三相輸入電源不平衡時，3P3W 系統由于自身電路拓撲結構無法給輸入不平衡電流提供零序電流通路，為了抑制輸入電流的畸變度和保證系統功率因數通常需要增加額外控制策略以滿足整流器性能要求[11-13]。因此，選擇合適的控制方法，可以使四橋臂-全橋拓撲形式的整流器（下文以三相四橋臂整流器進行表述）獲得相對于三相三橋臂系統以及三橋臂-分裂電容系統更加優異的性能。

本文通過開關平均周期法建立了三相四橋臂整流電路的開關平均數學模型，指出三相四橋臂整流器可以分解成三個解耦的單相整流電路。分析了三相四橋臂整流器使用常規的SPWM 控制策略所存在的不足，并針對該拓撲結構研究了采用3 次諧波注入法的SAPWM 控制策略。仿真和實驗表明，采用本文提出的控制策略下的三相四橋臂整流器具有優良的工作性能，特別是在三相輸入電源不平衡條件下，三相四橋臂整流器的優越性得到進一步體現。

2 三相四橋臂整流器系統建模

圖1b 所示為三相四橋臂整流器電路拓撲。其中eA、eB、eC為三相輸入電源，iLA、iLB、iLC為三相輸入電流，R為回路電阻，L為三相輸入濾波電感，Cf為直流側濾波電容，Udc為輸出直流電壓，RL為輸出負載電阻。

三相四橋臂整流器有八個開關器件，用sA、sB、sC、sN表示每個橋臂的開關函數。當橋臂上管開通，下管關斷時，定義此時橋臂的開關方式為si=1（i=A、B、C、N）；當橋臂下管開通；上管關斷時，定義此時橋臂的開關方式為si=0。按照這種定義，三相四橋臂整流器共有16 種開關模式，對應各開關模式時的橋臂電壓與輸出直流電壓，輸入電感電流與輸出電流的關系見表1。其中M0和M15為零開關模式，M1～M14為非零開關模式。

表1 三相四橋臂整流器開關模式Tab.1 Operation mode of three-phase four-leg rectifier

令sAN=sA-sN，sBN=sB-sN，sCN=sC-sN，則橋臂輸出電壓與直流側輸出電壓間的關系為

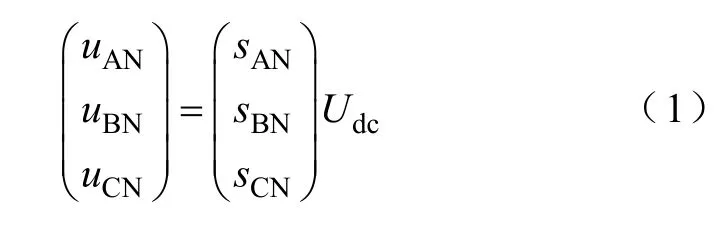
三相四橋臂整流器的狀態方程為

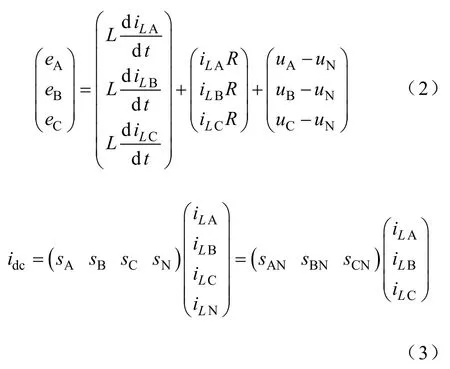
合并式（2）、式（3），整理后得

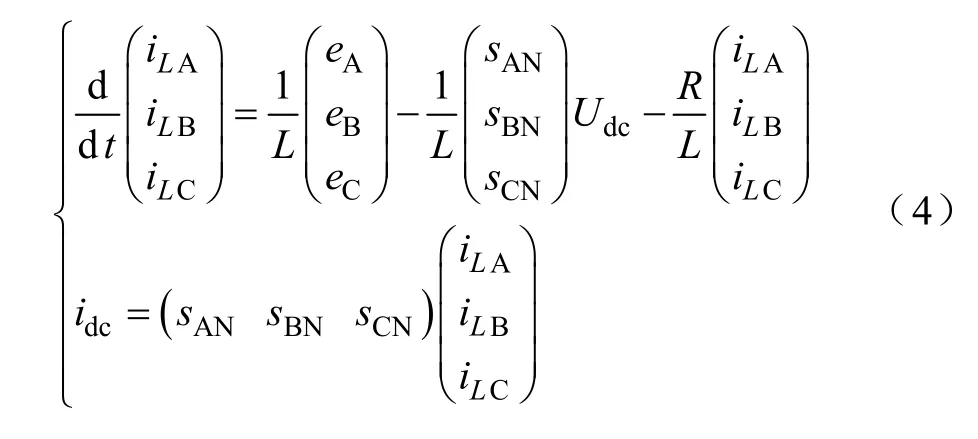
定義矢量

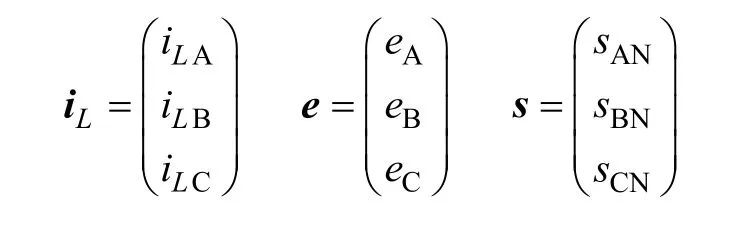
由開關周期平均法可得到

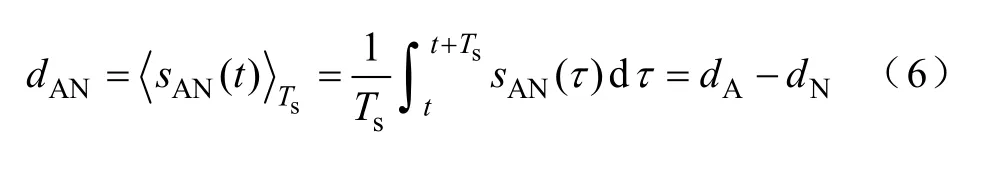
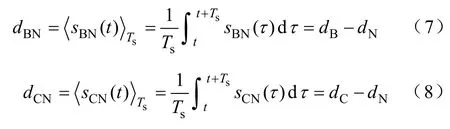
其中，di為第i個橋臂的占空比平均變量

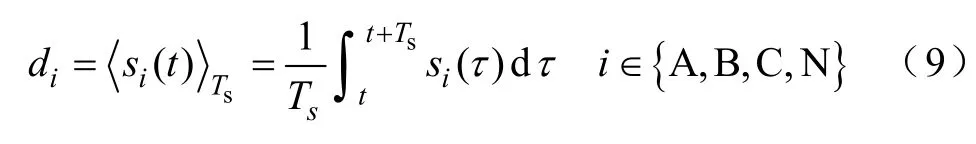
因為電感電流矢量iL為狀態變量，是關于時間的連續函數，且在一個開關周期內變化很小，故

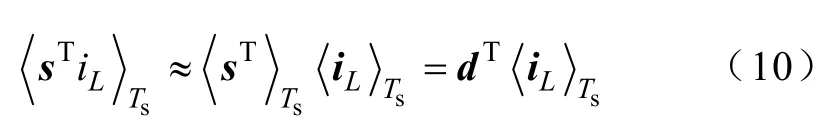
從而綜合式（5）～式（10），可以得到三相四橋臂整流器的開關周期平均模型

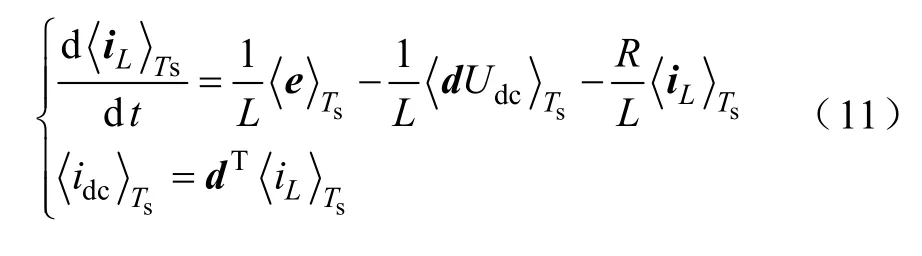
由式（11）可以得到三相四橋臂整流器的開關周期平均模型等效電路圖，如圖2 所示。

由此可以看出，相比較作為強耦合系統的三相三橋臂整流器，三相四橋臂整流器的每一相都是獨立的，相互之間不存在耦合關系，可以把三相四橋臂整流器分解成三個獨立的單向全橋整流器。特別是當三相輸入電源不平衡時，三相四橋臂整流器各相并不相互影響，采用傳統的電壓電流雙閉環控制策略時，每相輸入電感電流可以獨立跟蹤各相輸入電壓，從而在理論上表明，三相四橋臂整流器可以獲得較高的功率因數且輸入電流畸變度低。

3 三相四橋臂整流器控制策略

3.1 三相四橋臂整流器SPWM 控制策略

根據圖1b 所示的三相四橋臂整流器電路拓撲，設高頻三角載波的頻率為fs，幅值為1，整流器各橋臂上下管為互補導通，調制信號與高頻載波信號交截所得的脈沖控制下管，其反相控制上管。設四個橋臂調制信號分別為Ma、Mb、Mc、Mn。

假設三相輸入電壓源為標準正弦波

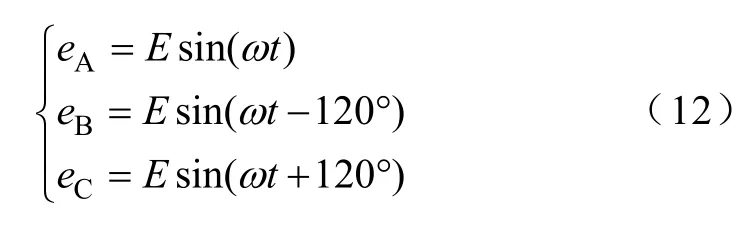
式中，E為輸入電源電壓的峰值；ω為輸入基波角頻率。

當采用SPWM 調制時，令各橋臂調制信號分別為

式中，m為調制比。

忽略開關死區及開關管管壓降等影響，各橋臂中點與輸出電容中點O 之間電壓的低頻分量uA(ωt)、uB(ωt)、uC(ωt)為

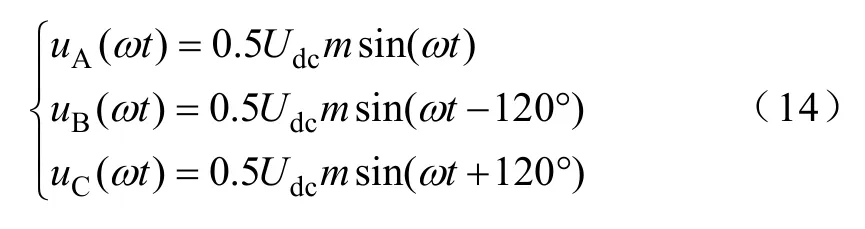
由于濾波電感L很小，除基波外電感電流iLA、iLB、iLC低頻分量很少，且高頻分量幅值也很小，故忽略輸入濾波電感上諧波壓降及線路壓降影響，從而有

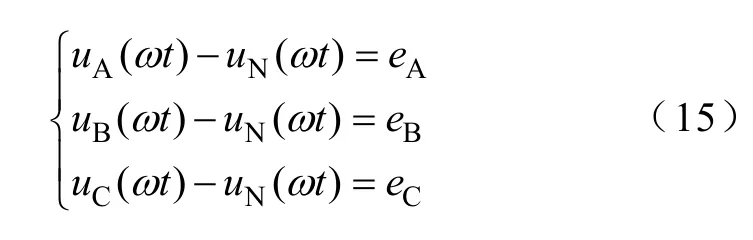
綜合式（14）和式（15）可得，直流側輸出電壓是由整流器前三個橋臂中點電壓uA、uB、uC決定。同時在三相四橋臂整流器中，由于第四橋臂的存在，使得iLA+iLB+iLC≠ 0，故uA、uB、uC又是由第四橋臂中點電壓uN與三相輸入電源電壓共同得出，其中uN是由第四橋臂的調制信號Mn決定，與其余各橋臂的調制信號Ma、Mb、Mc無關。

當三相四橋臂整流器前三個橋臂采用 SPWM控制策略，第四橋臂采用固定占空比控制時，由式（15）可得

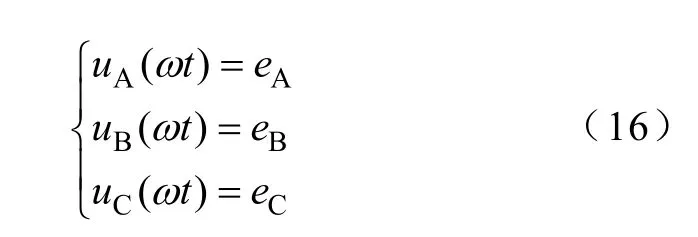
綜合式（12）、式（14）和式（16）可得

式（17）表明，三相四橋臂整流器采用SPWM控制策略時，其直流側輸出電壓需大于交流側輸入電源電壓峰值的2 倍。輸出電壓的提高進一步要求整流器的開關器件具有更高的耐壓等級，同時也延長了變換器功率管開關的導通時間，增加了變換器的導通損耗。

3.2 三相四橋臂整流器SAPWM 控制策略

由上述分析可知，為了降低整流器輸出電壓，必須改變整流器前三個橋臂的調制信號，使得各橋臂中點電壓降低，式（15）表明通過改變第四橋臂的調制信號可以實現這一目標。因此，本文提出采用SAPWM 控制策略實現對三相四橋臂整流器的控制。

3.2.1 SAPWM 調制波的傅里葉分析

圖3 所示的SAPWM 前半個周期的波形，其表達式可寫成

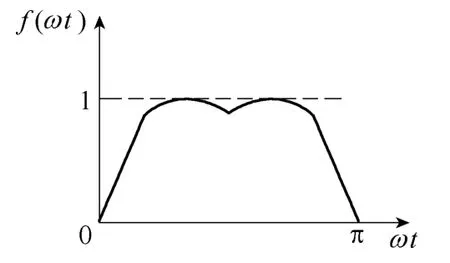
圖3 SAPWM 調制波形Fig.3 Modulation waveform of SAPWM

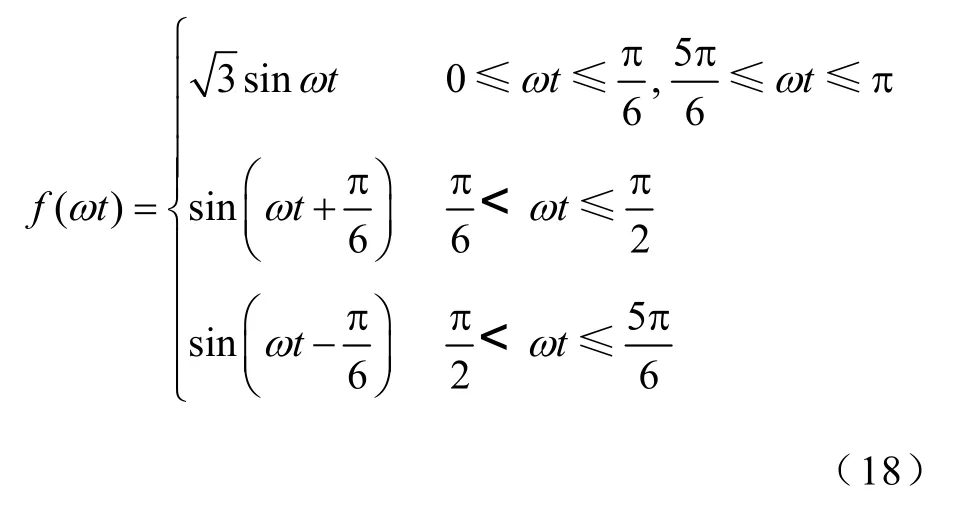
式（18）為定義在[0,π]上的函數，對它進行奇延拓可展開為正弦級數。故奇延拓后的函數傅里葉級數為[14]

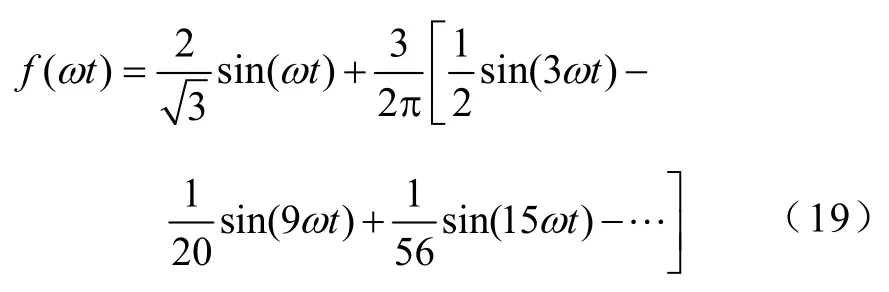
3.2.2 三相四橋臂整流器SAPWM 控制策略

對于三相四橋臂整流器采用SAPWM 控制策略框圖如圖4 所示。

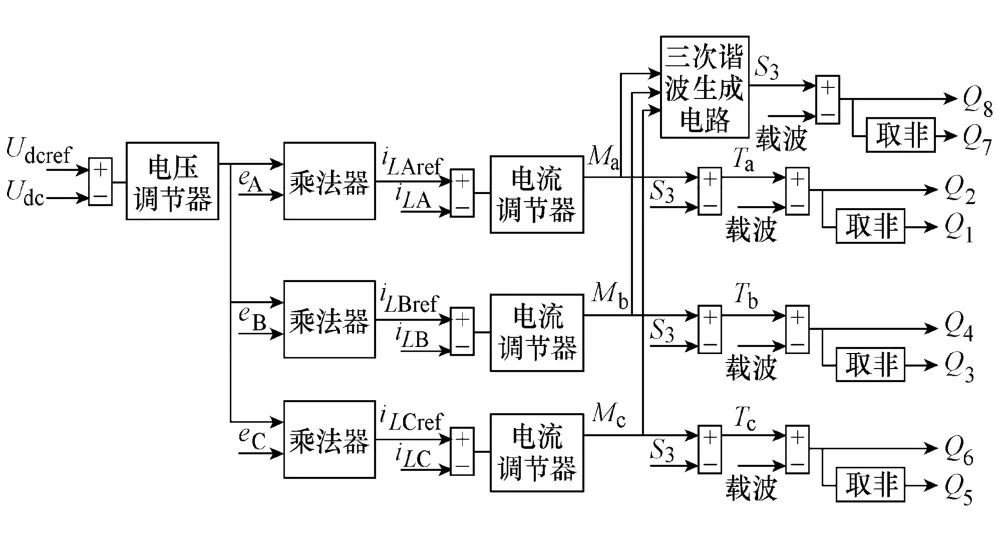
圖4 三相四橋臂整流器SAPWM 控制框圖Fig.4 SAPWM control block of three-phase four-leg rectifier

采用SAPWM 控制策略的三相四橋臂PWM 整流器采用電壓電流雙環控制，外環電壓環跟蹤直流輸出電壓基準，電壓環調節器輸出信號作為內環電流環電流給定的幅值基準，采樣輸入電源電壓作為電流給定的相位基準，二者通過乘法器最終獲得內環電流的給定信號。內環反饋整流器三相輸入濾波電感電流，使其跟蹤電流給定，將電流環輸出的正弦調制信號Ma、Mb、Mc經過3 次諧波生成電路構造成3 次諧波函數S3，并將其注入電流環輸出的正弦調制信號最終生成SAPWM 調制波Ta、Tb、Tc。將SAPWM 調制波Ta、Tb、Tc與載波交截所得的脈沖控制整流器前三個橋臂的下管，其反相信號控制相應的上管。第四橋臂直接由3 次諧波函數S3作為其調制信號。

SAPWM 控制策略下的各個橋臂的調制信號分別為

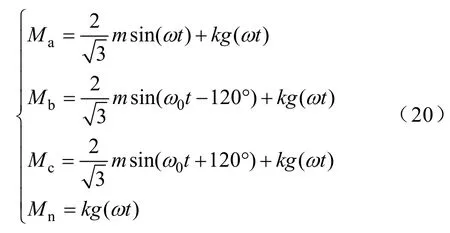
式中，k為3 次諧波注入系數，一般取0.15≤k≤0.2，g(ωt)為3 的奇數倍次諧波。

當采用SAPWM 控制策略時，整流器前三個橋臂與第四橋臂間電壓為

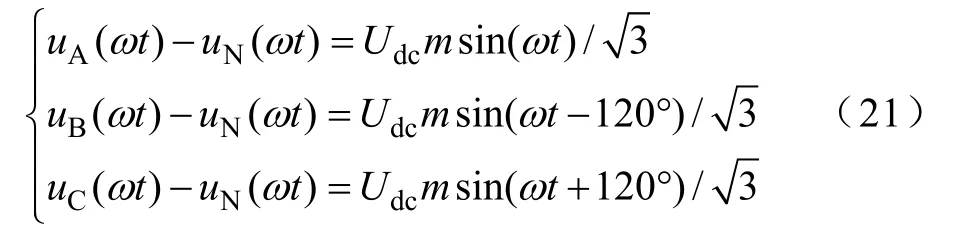
綜合式（12）與式（21）可得

式（22）表明采用SAPWM 控制策略時，三相四橋臂整流器直流側輸出電壓只需要大于輸入交流電源電壓峰值的倍，從而表明降低了直流側輸出電壓，提高了直流電壓利用率。

4 仿真及實驗驗證

為了驗證上述理論分析的正確性，在實驗室制作了一臺輸出功率為5kW 的三相四橋臂整流器原理樣機。其中輸入側三相交流電源電壓為 15V/400Hz，輸入濾波電感為240μH，輸出濾波電容為940μF，輸出直流電壓300V，開關頻率為25kHz。

圖5 為注入3 次諧波后的SAPWM 調制波仿真波形，其中圖5a 為電流環輸出的三相正弦調制信號及經過3 次諧波生成電路后生成的3 次諧波，圖5b為注入3 次諧波后的一相SAPWM 調制信號及載波。

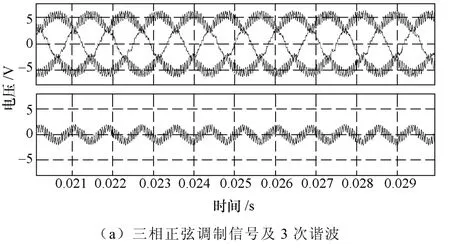
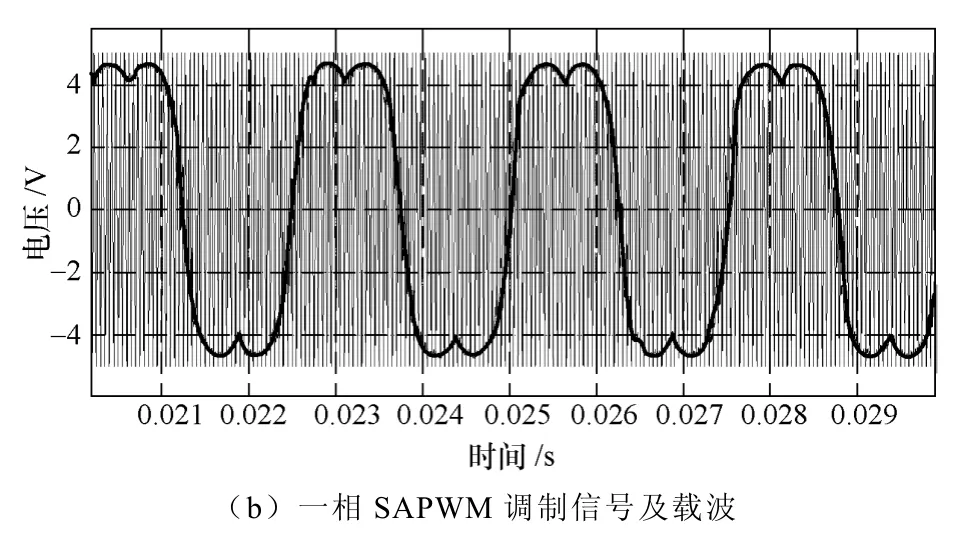
圖5 3 次諧波生成及SAPWM 調制仿真波形Fig.5 Simulation waveforms of three order harmonic and SAPWM modulation

4.1 三相電源輸入平衡時的實驗驗證

圖6 為輸入三相電源平衡時，三相四橋臂整流器工作時的主要電量穩態波形，其中圖6a 中分別是輸入三相電源平衡時A 相輸入電壓與A、B、C 三相輸入電流波形；圖6b 為三相輸入電流前10 次諧波頻譜；圖6c 為A、B 相橋臂電壓及輸出直流電壓波形。波形顯示三相四橋臂整流器橋臂間電壓在三個電平（-Udc，0，Udc）間跳變，相比較三橋臂-分裂電容整流拓撲對諧波具有較好抑制效果。表2 給出了相應的實測數據。波形及實測數據表明，輸入電流低次諧波含量較低，三相輸入電流THD＜4%，系統功率因數達到0.999，且輸出電壓很好的穩定在300V。

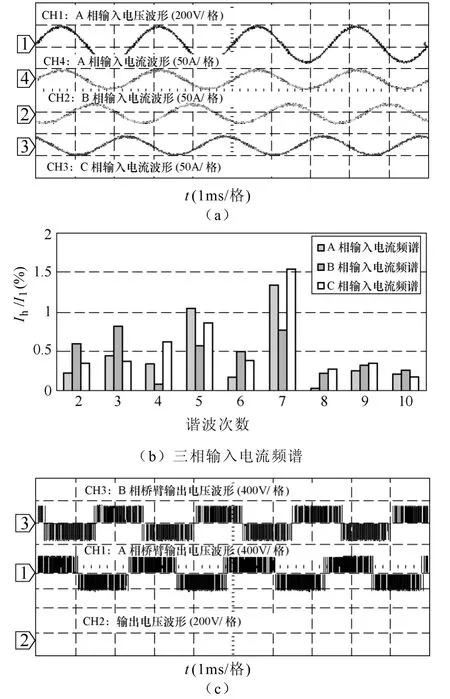
圖6 三相輸入平衡時，主要電量實驗波形Fig.6 The experiment waveforms with three-phase input balance

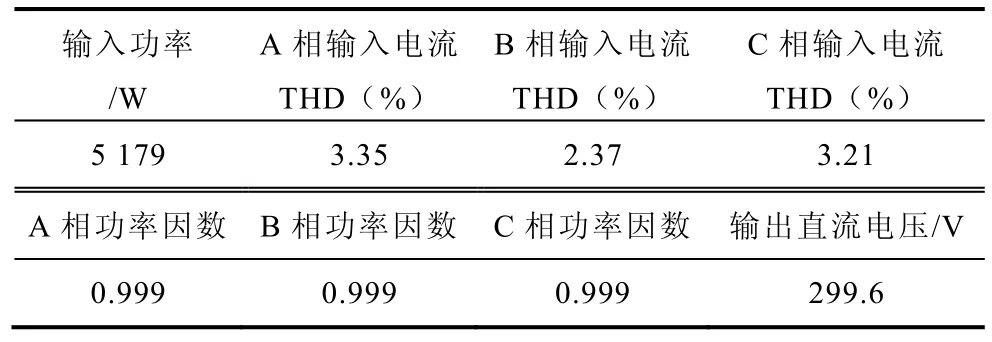
表2 三相輸入平衡時，部分電量實測數據Tab.2 Part of measured data with three-phase input balance

4.2 三相電源輸入不平衡時的實驗驗證

圖7 為三相四橋臂整流器在輸入三相電源幅值不平衡時的主要電量穩態波形，其中輸入電源電壓幅值分別為125V/105V/105V。圖7a 中分別為C 相輸入電壓、A、C 相及中線輸入電流波形；圖7b 為三相輸入電流前10 次諧波頻譜。表3 給出了相應的實測數據。波形及實測數據顯示在當前輸入電源不平衡度為 12.43%時，輸入電流低次諧波含量低且THD 小，系統功率因數高，直流輸出電壓穩定在300V 左右。

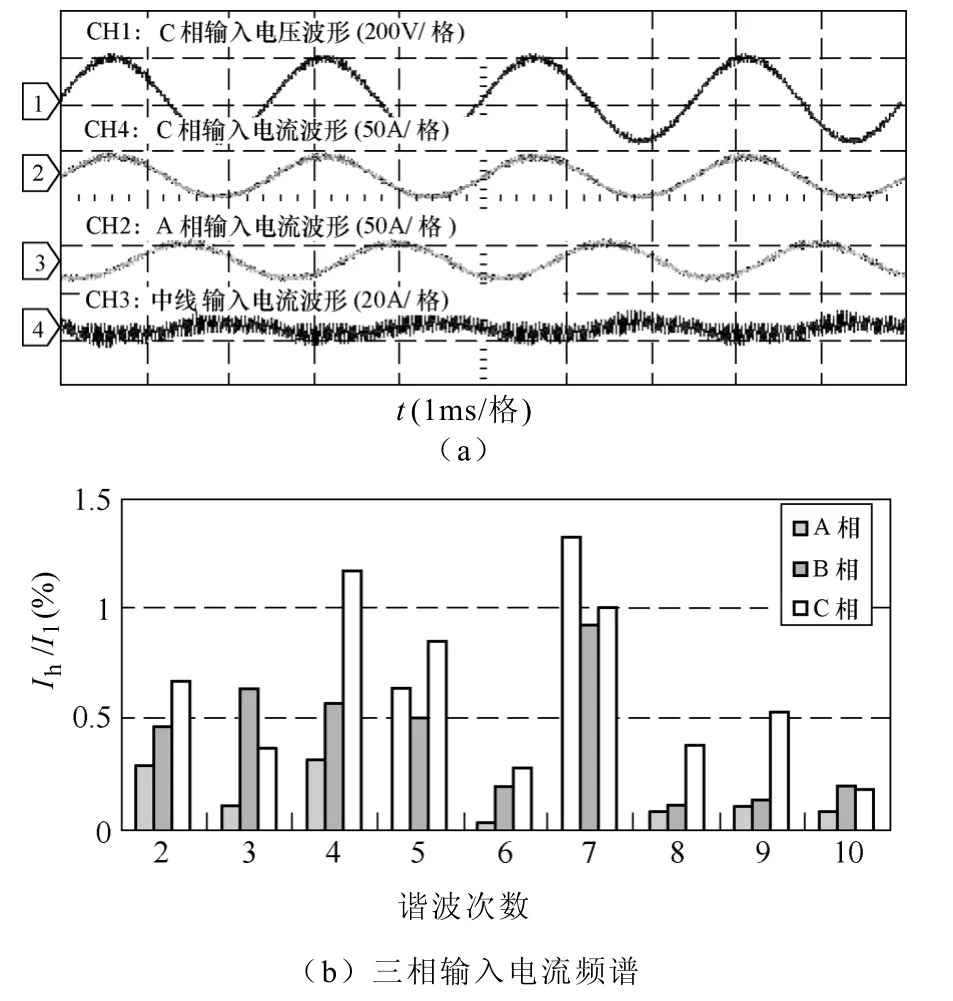
圖7 輸入電壓幅值不對稱下的實驗波形Fig.7 The experiment waveforms with three-phase input amplitude unbalance

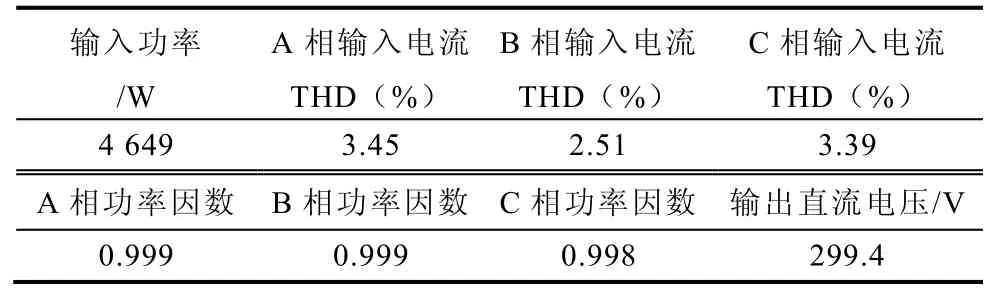
表3 三相輸入幅值不平衡時，部分電量實測數據Tab.3 Part of measured data with three-phase input amplitude unbalance

圖8 為三相四橋臂整流器在輸入三相電源相位不平衡時的主要電量穩態波形，其中輸入電源電壓相位分別為0o、116o、244o。圖中分別為C 相輸入電壓、A、C 相及中線輸入電流波形。表4 給出了相應的實測數據。波形及實測數據顯示在當前輸入電源相位不平衡條件下，輸入電流低次諧波含量低且THD 小，系統功率因數高，直流輸出電壓穩定在300V 左右。

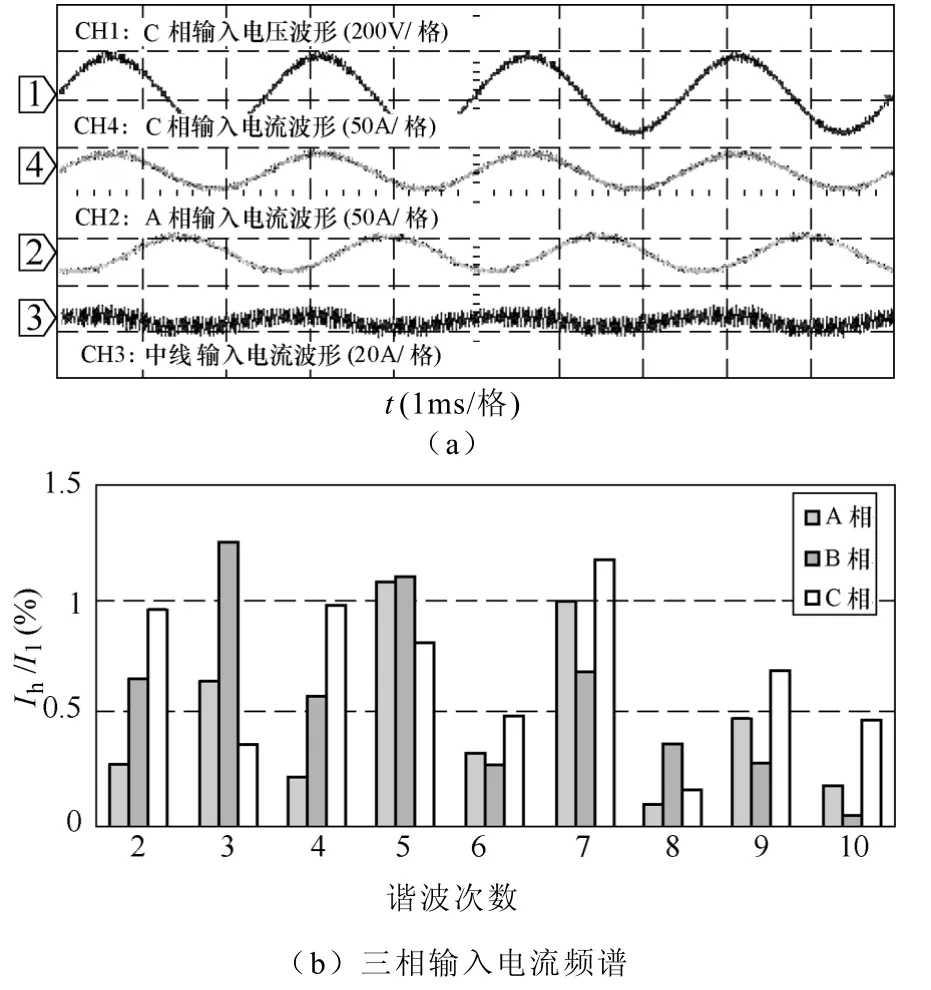
圖8 輸入電壓相位不對稱下實驗波形Fig.8 The experiment waveforms with three-phase input phase unbalance

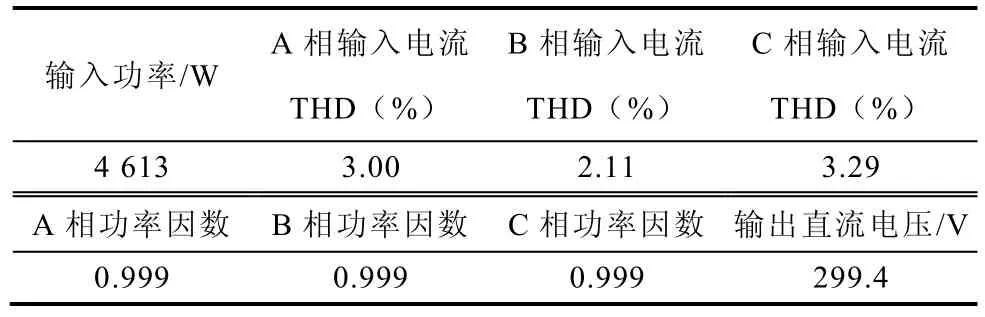
表4 三相輸入相位不平衡時，部分電量實測數據Tab.4 Part of measured data with three-phase input phase unbalance

圖9 為三相四橋臂整流器在輸入三相電源一相短路時的主要電量穩態波形，圖中分別為C 相輸入電壓、A、B 相輸入電流、直流輸出波形。表5 給出了相應的實測數據。波形及實測數據顯示在輸入三相電源一相短路時的極端工作條件下，正常輸入兩相依然保持很高的功率因數且輸入電流THD 小，直流輸出電壓穩定在300V 左右。

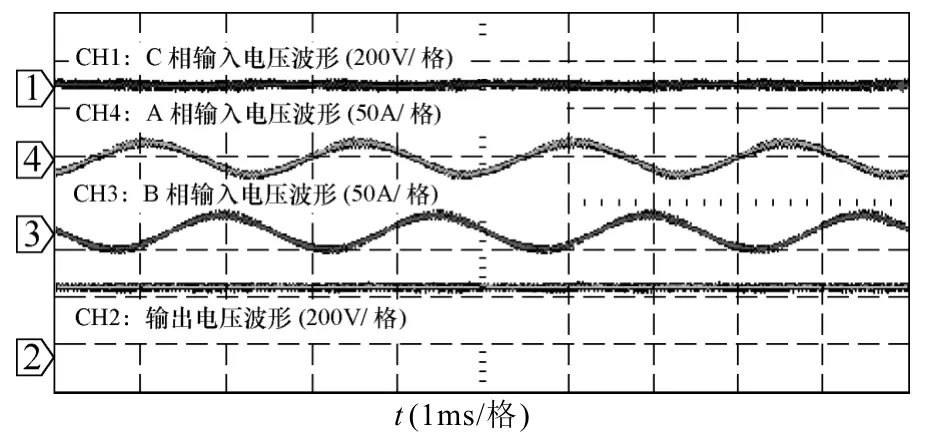
圖9 一相輸入短路時，主要電量實驗波形Fig.9 The experiment waveforms with one phase input short circuit

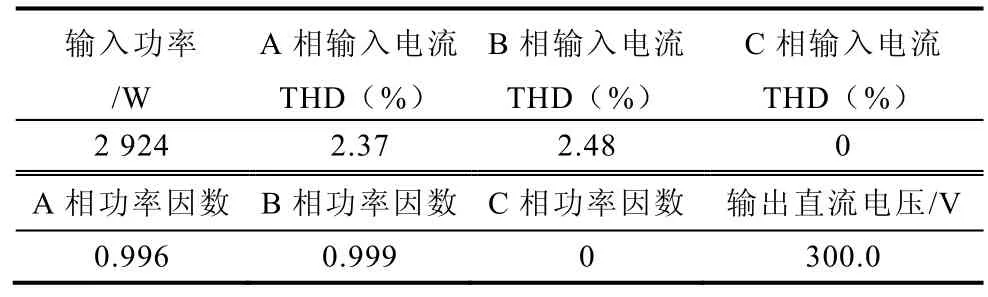
表5 一相輸入短路時，部分電量實測數據Tab.5 Part of measured data with one phase input short circuit

輸入三相電源不平衡下的實驗表明，三相四橋臂整流器在輸入三相電源不平衡甚至在一相輸入短路的工況下，依然能保證很高的系統功率因數且輸入電流THD 小。相比較傳統的三相三橋臂整流器在輸入三相電源不平衡情況下其交流側出現的較大比例的3、5、…等奇次非特征諧波電流分量[15]，三相四橋臂整流器輸入電流低次諧波含量較低，其性能優勢更為明顯。

5 結論

通過開關平均周期法對三相四橋臂整流器建立了開關平均模型，指出三相四橋臂整流器可以分解成三個相互解耦的單相整流電路，從而表明相對于三相三橋臂整流器在輸入電源不平衡工況下具有更好的工作性能。

分析了三相四橋臂整流器在SPWM 控制策略下的不足，研究了系統SAPWM 控制策略及其實現方法。基于SAPWM 控制的三相四橋臂整流器降低了直流輸出電壓，提高了直流母線電壓利用率，進而有助于降低元器件耐電壓等級。仿真與實驗結果表明理論分析的正確性。

[1]方宇,裘迅,邢巖,等.基于預測電流控制的三相高功率因數PWM 整流器研究[J].中國電機工程學報,2006,26(20):69-73.Fang Yu,Qiu Xun,Xing Yan,et al.Research on three-phase high power factor correction based on predictive digital current controller[J].Proceedings of the CSEE,2006,26(20):69-73.

[2]方宇,裘迅,邢巖,等.三相高功率因數電壓型PWM 整流器建模和仿真[J].電工技術學報,2006,21(10):44-49.Fang Yu,Qiu Xun,Xing Yan,et al.Modeling and simulation of three phase high power factor PWM rectifier[J].Transactions of China Electrontechnical Society,2006,21(10):44-49.

[3]Luigi Malesani,Paolo Tomasin,Vanni Toigo.Space vector control and current harmonics in quasiresonant soft-switching PWM conversion[J].IEEE Transactions on Industry Applications,1996,32(2):269-277.

[4]Mobin S,Hiraki E,Takano H,et al.Simulation method for DSP-controlled active PFC high-frequency power converters[J].IEEE Electric Power Applications,2000,147(3):159-166.

[5]Noguchi T,Tomiki H,Kondo S.Direct power control of PWM converter without power-source voltage sensor[J].IEEE Transactions on Industry Applications,1998,34(3):473-479.

[6]張穎超,趙爭鳴,袁立強,等.三電平PWM 整流器直接功率控制[J].電工技術學報,2008,23(5):62-68.Zhang Yingchao,Zhao Zhengming,Yuan Liqiang,et al.Direct power control for three-level PWM rectifier[J].Transactions of China Electrotechnical Society,2008,23(5):62-68.

[7]Malinowski M,Kazmierkowski M P,Blaabjerg F,et al.Virtual-flux-based direct power control of threephase PWM rectifiers[J].IEEE Transactions on Industry Applications,2001,37(4):1019-1027.

[8]楊德剛,劉潤生,趙良炳.三相高功率因數整流器的電流控制[J].電工技術學報,2000,15(2):83-87.Yang Degang,Liu Runsheng,Zhao Liangbing.Current controller design of a three-phase highpower-factor rectifier[J].Transactions of China Electrotechnical Society,2000,15(2):83-87.

[9]陳瑤,金新民,童亦斌.三相四線系統中三相電壓型PWM 整流器控制策略[J].電工技術學報,2007,22(7):64-69.Chen Yao,Jin Yu,Xinmin,Tong Yibin.Control strategy of three-phase voltage source PWM rectifier in three-phase four-wires systems[J].Transactions of China Electrotechnical Society,2007,22(7):64-69.

[10]陳瑤,金新民,童亦斌.三相四線系統中SPWM 與SVPWM 的歸一化研究[J].電工技術學報,2007,22(12):123-129.Chen Yao,Jin Yu,Xinmin,Tong Yibin.Study of the unification of SPWM and SVPWM in three-phase four-wires systems[J].Transactions of China Electrotechnical Society,2007,22(12):123-129.

[11]Rioual P,Pouliquen H,Louis J.Regulation of a PWM rectifier in the unbalanced network state using a generalized model[J].IEEE Transactions on Power Electronics,1996,11(5):495-502.

[12]Hong-seok Song,Kwanghee Nam.Dual current control scheme for pwm converter under unbalanced input voltage conditions[J].IEEE Transactions on Industry Applications,1999,46(5):953-959.

[13]Stankovic A V,Lipo T A.A novel control method for input output harmonic elimination of the PWM boost type rectifier under unbalanced operating conditions[J].IEEE Transactions on Power Electronics,2001,16(5):603-611.

[14]陳國呈.新型電力電子變換技術[M].北京:中國電力出版社,2004.

[15]Lusi Moran,Phoivos D Ziogas,Geza Joes.Design aspects of synchronous PWM rectifier-inverter systems under unbalanced input voltage condition[J].IEEE Transactions on Industry Applications,1992,28(6):1286-1294.