雙三相感應電動機矢量控制調速系統建模與仿真

張 岳，沈建新

(浙江大學，杭州 310027)

0 引 言

近年來，隨著電力電子技術的發展，多相電機驅動系統相比普通三相系統顯示出了不少特有的優勢，因而越來越廣泛地被應用于需要高功率、高可靠運行的場合，如新能源汽車牽引、船舶推進等［1－3］。其中，作為一種常見的多相電機系統，雙三相感應電動機具有兩套對稱的、空間位置互差30°電角度、中心點相互獨立的三相星形連接定子繞組［4－5］，制造成本較低。研究表明這種雙三相感應電動機不僅能夠有效消除轉矩脈動中的六次分量，同時也能夠通過減少轉子電流諧波分量來降低轉子損耗［6］。雙三相感應電動機系統還能夠減少直流母線電流的諧波含量，提高整個系統的穩定性［7］。

針對雙三相感應電動機調速系統的研究，目前的文獻大多從產生多電平的角度介紹了雙三相感應電動機驅動技術［8－9］;或者將電機模型在靜止坐標系下進行變換，從而對雙三相感應電動機進行控制［10－12］。上述方法雖然能夠較好地控制雙三相感應電動機的運行性能，但是存在計算模型及相應的控制策略復雜的問題。基于此，本文首先建立雙三相感應電動機在靜止坐標系下的模型;在此基礎上針對該電機的繞組特點，推導了在同步旋轉的正交坐標系下的數學模型，在這個旋轉坐標系下雙三相電機繞組能夠實現高性能的解耦控制;研究雙三相感應電動機轉子磁場定向的矢量控制方法，并建立矢量調速系統的仿真模型。仿真結果表明，本文介紹的雙三相感應電動機矢量控制系統具有優良的動態運行性能。

1 雙三相感應電動機數學模型

1.1 原坐標系模型

(1)磁鏈模型

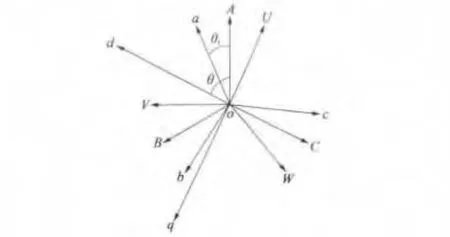
圖1 雙三相感應電動機定、轉子繞組軸線矢量圖

雙三相感應電動機定、轉子繞組軸線矢量關系如圖1所示。其中定子繞組分別標記為A－B－C及U－V－W;轉子繞組經歸算后的等效繞組為a－b－c。則電機定子、轉子間的自感和互感具有如下關系。

定子自感:

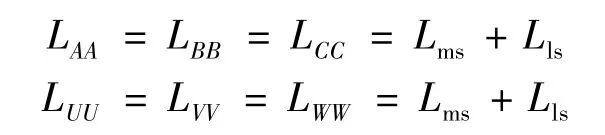
轉子自感:

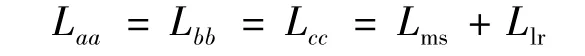
式中:Lms為勵磁電感;Lls、Llr分別為定轉子繞組漏感。定子繞組間電感(忽略定子繞組間互漏感):

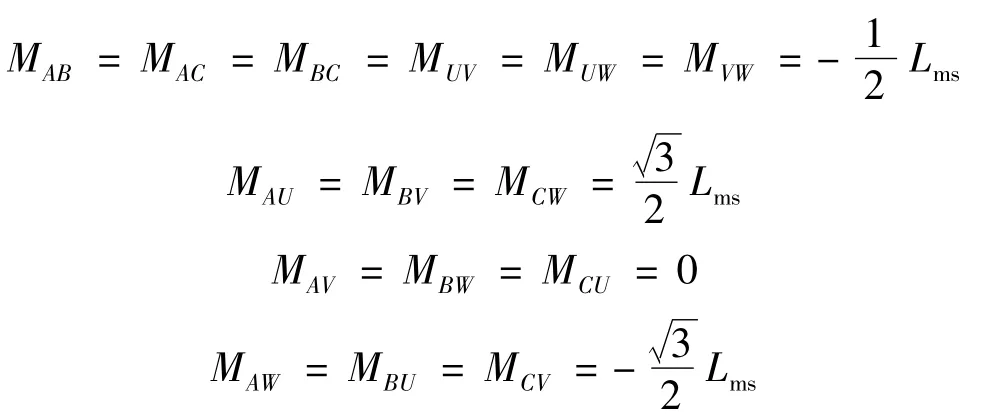
定、轉子間互感:

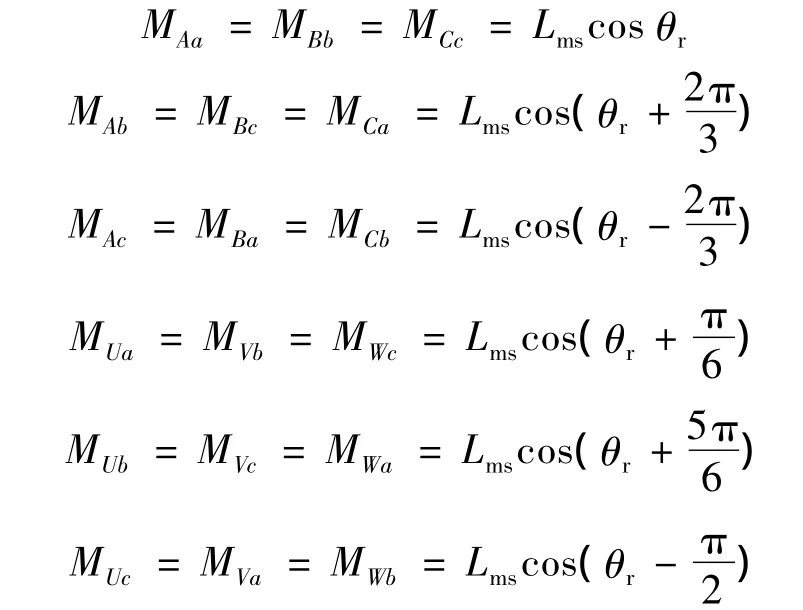
式中:θr為轉子位置空間角度，即轉子a相繞組與定子A相繞組軸線間的夾角;iA和iU分別為定子繞組A相與U相電流;ia為歸算到定子邊的轉子a相電流，其余以此類推。由此可得電機磁鏈方程:

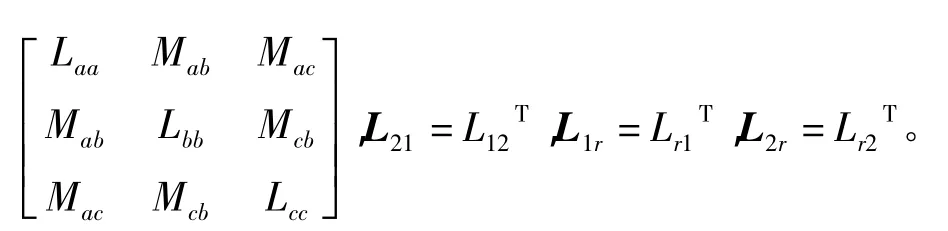
(2)電壓方程

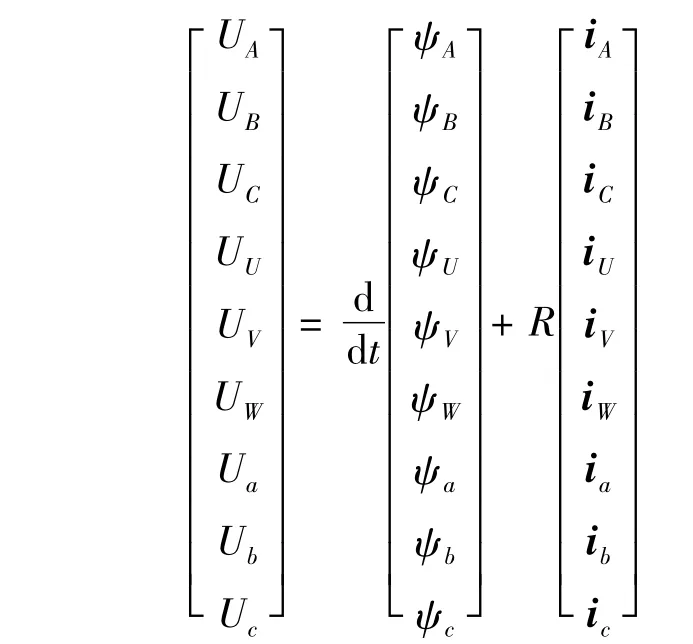
雙三相感應電動機的電磁轉矩為Te，由機電能量轉換的原理，電機的電磁轉矩等于機械角位移變化時磁共能的變化率，因此雙三相感應電動機電磁轉矩Te的表達式經整理后:

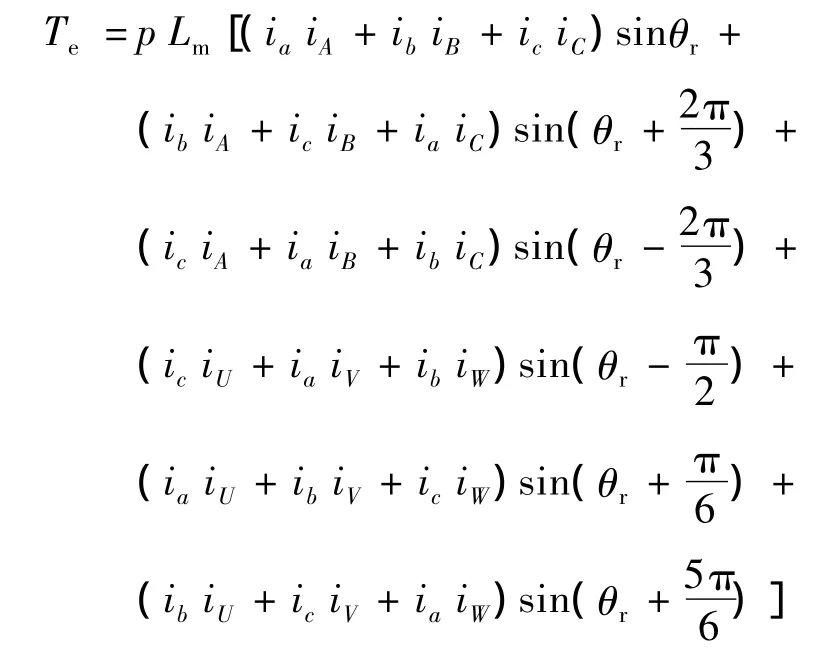
式中:p為電機極對數。

運動方程:

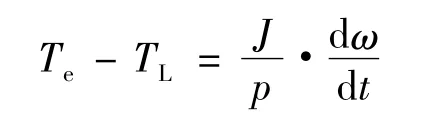
式中:TL為電機的負載與阻尼轉矩之和;J為電機轉動慣量;Ω為電機的機械轉速。

式中:從以上推導的電機模型可以看到，雙三相感應電動機是一種非線性、強耦合的系統。從電壓方程、磁鏈方程中看到，不僅存在定子、轉子之間的耦合，還存在定子繞組間的交叉耦合;轉矩方程中包含狀態變量之間的乘積項。這些系統復雜性與高度耦合性都給電機控制帶來很大困難。

1.2 雙三相感應電動機雙dq坐標系下的模型

為了解決雙三相電機的耦合問題，文獻［10－12］通過一個坐標變換矩陣，將電機分解到三個二維的子坐標系統。考慮到雙三相感應電動機的繞組是由兩套相互獨立的三相繞組構成的特點，可以采用三個三維的坐標變換矩陣，將兩套定子繞組和一套轉子繞組分別以不同的坐標變換矩陣變換到同一套以同步速旋轉的d，q坐標系上，或者說變換后的第一套定子繞組的d軸、第二套定子繞組的d1軸與轉子繞組的dr軸是重合的，都位于同步速旋轉的d，q坐標系的d軸上，一起以同步速旋轉。

在這里假設電機的繞組是對稱并且正弦分布的，同時忽略電機互感中的漏感及鐵心損耗。電機兩套定子繞組的坐標變換矩陣分別如下:

將靜止的A，B，C繞組變換到同步速ω旋轉的d，q坐標系的變換矩陣:

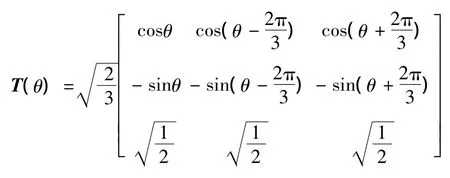
將靜止的U，V，W繞組變換到同步速ω旋轉的d，q坐標系變換矩陣:

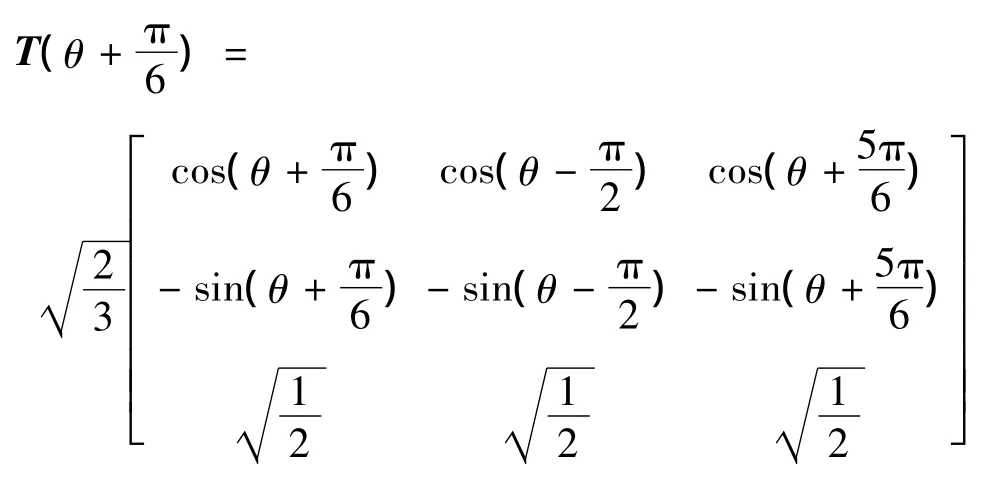
根據上述坐標變換矩陣，將電機的定、轉子矩陣變換到同步速旋轉坐標系的d，q軸上。那么經過變換后，電機的磁鏈方程、電壓方程、轉矩方程分別如下所示。

磁鏈方程:

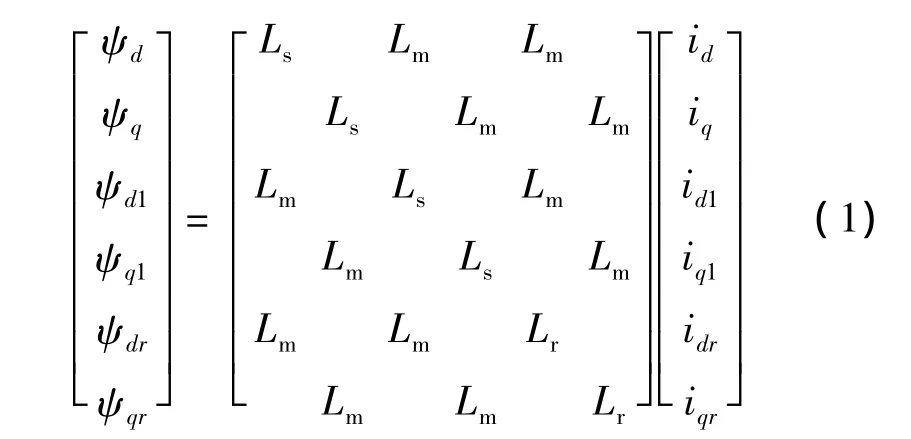
電壓方程:

任意速旋轉坐標系Ω下的雙三相感應電動機電壓模型如下:

轉矩方程:

只有旋轉電勢和相應電流的乘積等于與電磁轉矩對應的電磁功率，因此經坐標變換推導后，雙三相感應電動機的電磁轉矩方程:

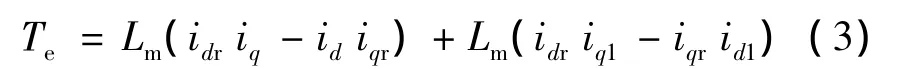
從式(1)～式(3)可以看到，這種將雙三相電機繞組分解到旋轉的d，q坐標系上的方法，使得雙三相感應電動機電壓和磁鏈方程中的各個量成為與電機轉子位置無關的常數。同時，電機電磁轉矩成為了與正交坐標系下解耦的定子、轉子繞組電流相關的變量，從而實現了雙三相電機的解耦，同時大大簡化了電機模型，為實現雙三相感應電動機的矢量控制打下了良好基礎。

2 雙三相感應電動機磁鏈觀測模型

根據上節介紹的雙三相感應電動機在d，q坐標系下的數學模型，同時考慮到轉子采用鼠籠轉子的形式，那么udr=uqr=0;同時，以轉子磁場矢量的方向作為 d軸，就可以得到:Ψdr=Ψr，Ψqr=0，由此電機轉子磁鏈方程和電壓方程:

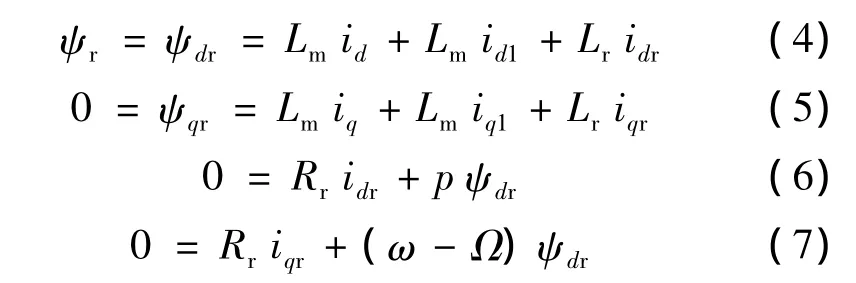
將式(6)帶入式(4)可以得到雙三相感應電動機的轉子磁鏈:

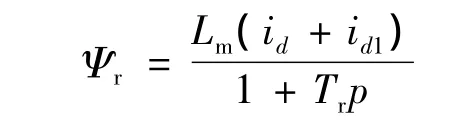
式中:Tr為轉子電氣時間常數，其定義:

同時本文定義勵磁電流:

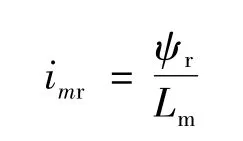
由式(7)與式(5)經整理后可以得到:

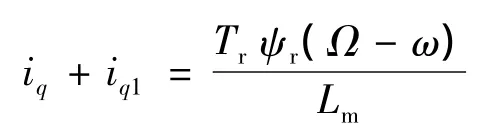
因此雙三相感應電動機的轉差ωf可以表示:

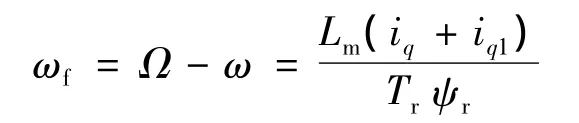
則轉子磁鏈的相位:

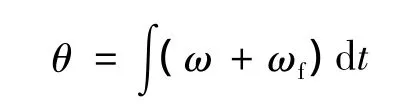
3 雙三相感應電動機矢量控制系統仿真

根據上面介紹的雙三相感應電動機模型及轉子磁鏈觀測的基本方法，針對一臺3.6 kW的雙三相感應電動機，如表1所示，設計了按轉子磁場定向的矢量控制調速系統，控制系統框圖如圖2所示，其中磁鏈按照磁鏈的標么值給定。當電機運行在高速區時，可以通過減小磁鏈給定值的方法達到弱磁調速的目的;轉矩給定值指電機負載轉矩。

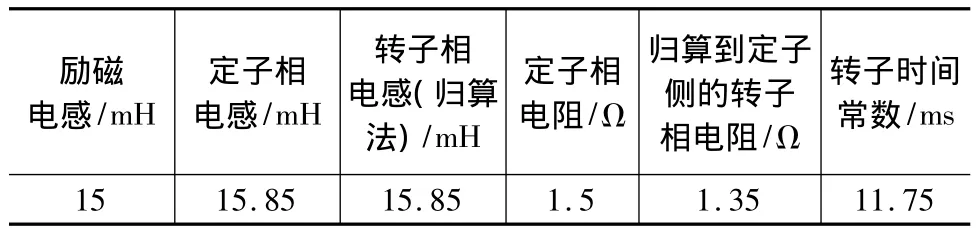
表1 雙三相感應電動機參數

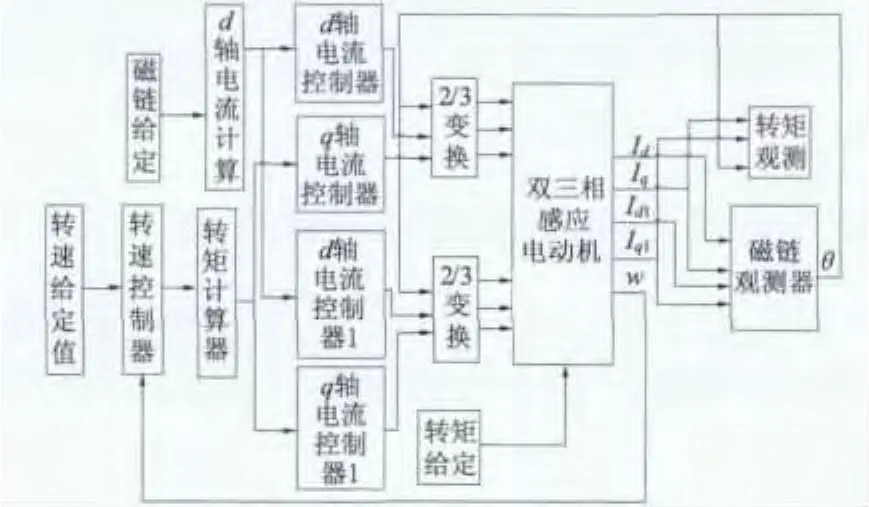
圖2 雙三相感應電動機調速系統

控制系統采用轉速、電流雙閉環控制技術，該控制系統的原理如下:首先，電機的給定轉速與實際轉速反饋值經過轉速控制器的PI調節得到轉矩給定值，并輸入到轉矩計算器模塊得到q軸電流給定值;磁鏈給定值經過d軸電流計算模塊得到的結果分別輸入d軸電流控制器和d軸電流控制器1。d軸電流計算模塊與轉矩計算器模塊均是按照本文介紹的雙三相感應電動機在旋轉dq軸模型下的數學模型確立的。磁鏈觀測器模塊則是根據電機轉子磁鏈觀測模型，計算得到了相應時刻轉子磁鏈的空間位置。以上所得的各個電流給定值經過電流控制器模塊計算可以得到各自的電壓給定值，經過Park變換和Clarke變換(3/2變換)得到了在靜止坐標系下電機各相的供電電壓。在本文的仿真過程中，電機機械轉速給定值為60 rad/s，仿真時間為1.2 s。首先，電機空載起動，在0.4 s時刻負載轉矩達到60 N·m;在電機起動后0.8 s時刻電機的負載轉矩下降到30 N·m。

在圖2的控制方式下，雙三相感應電動機的轉速、轉矩隨時間變化的曲線如圖3和圖4所示;轉子磁鏈標么值隨時間變化軌跡及轉子磁鏈圓軌跡分別如圖5和圖6所示。

圖3 起動和負載突變時的轉速變化

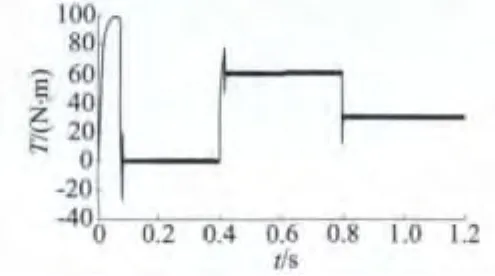
圖4 起動和負載突變時的轉矩變化

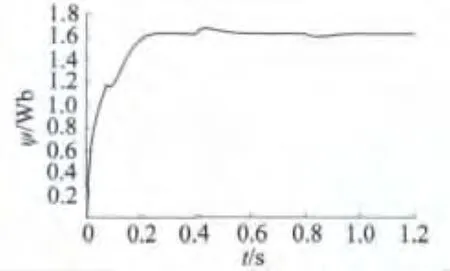
圖5 轉子磁鏈標么值－時間變化曲線

圖6 轉子磁鏈圓軌跡

通過以上仿真結果可以看到，電機空載起動，其轉速響應在這個過程中超調很小，如圖3所示，經過約90 ms的時間，電機轉速響應到達了轉速給定值60 rad/s;在電機起動0.4 s后，電機負載轉矩突增，轉矩響應經調整能夠迅速達到負載轉矩60 N·m;0.8 s時電機的負載轉矩下降到30 N·m，轉矩響應也能夠快速跟蹤負載轉矩的變化達到新的穩定值。同時，在以上負載轉矩切換的過程中，電機的轉速響應能夠一直穩定在60 rad/s的給定值。圖3的轉速波形及圖4的轉矩曲線表明，電機的轉速脈動和轉矩脈動都比較小，整個調速系統具有較好的動態和靜態性能。

4 結 語

根據雙三相感應電動機在靜止坐標系下的數學模型，通過恰當的坐標變換，將雙三相感應電動機的兩套定子繞組和轉子繞組變換到以同步速旋轉的坐標系上;然后以電機轉子磁場矢量的方向作為d軸，能夠使原靜止坐標系下耦合的雙三相感應電動機的數學模型在該旋轉坐標系上達到解耦的目的;根據上述電機模型，設計了雙三相感應電動機矢量控制系統，其仿真結果表明，該調速系統具有良好的動態和穩態性能，適用于對雙三相感應電動機的控制。

［1］LEVI E.Multiphase electric machines for variable speed applications［J］.IEEE Transactions on Industrial Electronics，2008，55(5):1893－1909.

［2］PARSA L.On advantages of multi－ Phase machines［J］.Industrial Electronics Society，2005，13(2):1574 －1579.

［3］劉東，黃進，楊家強.多相感應電機轉子磁場定向矢量控制策略［J］.浙江大學學報(工學版)，2012，46(8):1498 －1505.

［4］許實章.交流電機的繞組理論［M］.北京:機械工業出版社，1985.

［5］ALFREDO R M，THOMAS A L.Dual stator winding induction machine drive［J］.IEEE Transactions on Industrial Applications，2000，36(5):1369 －1379.

［6］NELSON R H，KRAUSE P C.Induction machine analysis for arbitrary displacement between multiple winding sets［J］.IEEE Transactions on Power Apparatus and Systems，1974，93(3):841 －848.

［7］BOJOI R，TENCONI A，PROFUMO F.Complete analysis and comparative study of digital modulation techniques for dual three－ phase AC motor drives［J］.Power Electronics Specialists Conference，2002，2:851 －857.

［8］GIERSE G，SCHUERMANN W.Microprocessor control for two magnetically coupled three － phase PWM inverters［J］.IEEE Transactions on Power Electronics，1986(3):141 －147.

［9］HADIOUCHE D，BAGHLI L.Space － vector PWM techniques for dual three － phase AC machine:analysis，performance evaluation，and DSP implementation［J］.IEEE Transactions on Power Electronics，2006，42(4):1112 －1122.

［10］ZAIMEDDINE R，UNDELAND T.Direct torque control scheme for Dual Three Phase induction motor［C］//Power Electronics Conference(IPEC)，Sapporo，2010，21 －24:3007 －3014.

［11］LI Shan，XIAO Huihui.Research of SVPWM control technique of double three － phase induction motor［C］//Electrical Machines and System 2005(ICEMS 2005)，2005:109 －114.

［12］BOJOI R，LAZZARI M.Digital field oriented control for dual three phase induction motor drives［J］.IEEE Transactions on Industrial Electronics，2003，39(3):752－760.