基于遺傳算法的靜電微電機優(yōu)化設計

宮香山，劉曉偉，何廣平

(1.北京郵電大學，北京 102613;2.中國航天空氣動力技術研究院，北京 100074;3.北方工業(yè)大學，北京 100144)

0 引 言

靜電微電機是一類具有廣泛應用前景的重要MEMS 器件，可用于靜電微陀螺［1］、微操作器［2］、微創(chuàng)醫(yī)療器械［3］，以及燃料分配、藥物精確投放和微流體驅(qū)動應用中的微泵［4］。可變電容式靜電微電機是最早提出的一類靜電微電機［5］，它利用電機定子和轉(zhuǎn)子之間的電容變化來獲得輸出力矩。這種微電機的缺點是靜電力很微小，動態(tài)性能十分有限，所以近年來，針對它的優(yōu)化設計得到了部分學者的關注［6－7］。

本文針對頂面驅(qū)動可變電容式靜電微電機，提出了一種優(yōu)化設計方法。這種方法也可用于其他類型的凸極式靜電微電機的優(yōu)化設計。該方法不僅考慮了電機控制方法的優(yōu)化，還結(jié)合了數(shù)值積分方法和遺傳算法對電機的結(jié)構(gòu)參數(shù)進行了優(yōu)化。試驗表明，這種優(yōu)化設計方法提高了電機的輸出力矩，同時大幅減小了輸出力矩的波動。

1 頂面驅(qū)動靜電微電機的數(shù)學模型

設頂面驅(qū)動可變電容靜電微電機的定子和轉(zhuǎn)子都是均布的凸極結(jié)構(gòu)，如圖1所示，且電機有np個定子電極，nr個轉(zhuǎn)子凸極。

圖1 頂面驅(qū)動靜電微電機的結(jié)構(gòu)原理圖

定子電極內(nèi)緣和外緣半徑分別為R1和R2，電極所占角度為φ1，電極間隔角度為φ2。

轉(zhuǎn)子凸極內(nèi)緣和外緣半徑分別為r1和r2，轉(zhuǎn)子凸極所占的角度為α1，轉(zhuǎn)子凸極間的夾角為α2。

基于以上設計，該電機定子相鄰兩電極之間的相位差:

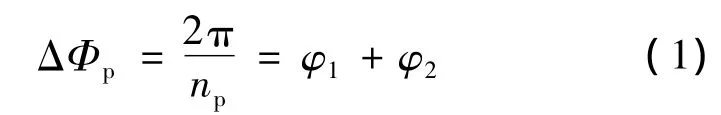
電機轉(zhuǎn)子相鄰兩凸極之間的相位差:

設定子電極的內(nèi)徑不小于轉(zhuǎn)子凸極的內(nèi)徑，即R1≥r1，且定子電極的外徑與轉(zhuǎn)子凸極外徑相等，即r2=R2。則轉(zhuǎn)子和定子之間的電容可表示:

式中:εr為相對介電常數(shù);ε0為真空絕對介電常數(shù)，ε0=8.85×10－12F/m;d 為電機轉(zhuǎn)子與定子之間的軸向距離;θ為轉(zhuǎn)子轉(zhuǎn)動的角度;A(θ)為轉(zhuǎn)子凸極與定

子電極之間的重疊面積。采用極坐標表示方法，A(θ)可表示:式中:α表示轉(zhuǎn)子上任意一點在固聯(lián)于轉(zhuǎn)子上的極坐標系中的相對角坐標;θ則為轉(zhuǎn)子轉(zhuǎn)動角度在慣性坐標系中的表示，因此α+θ表示轉(zhuǎn)子上任意一點在慣性極坐標系中的角坐標。若定義:

則式(4)中的函數(shù)f(α+θ)和g(α)可表示:

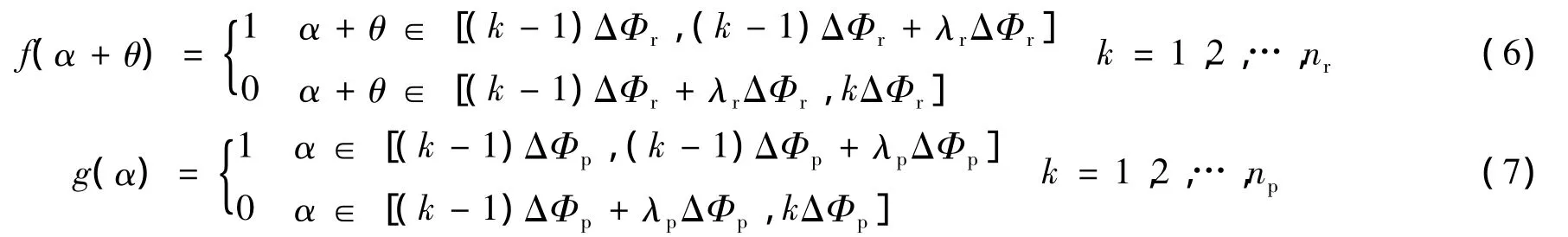
顯然，式(6)和式(7)分別表示轉(zhuǎn)子凸極和定子電極沿圓周方向是否存在，當存在于對應區(qū)間上時f(α+θ)和g(α)為1，對應區(qū)間上不存在轉(zhuǎn)子凸極或定子電極時則為0。而式(8)表示對應定子電極是否施加了非零電壓。當施加了非零電壓時(用ΔΦp(k)表示)，β(α)為1，否則(用Δ(k)表示)，β(α)為零。考慮電機定子電極和轉(zhuǎn)子凸極分布的均勻性，式(4)還可進一步表示:

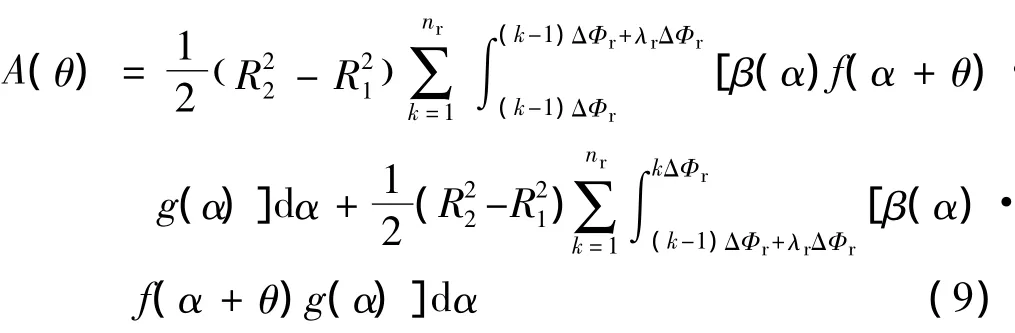
靜電微電機中存儲的電能可表示:

式中:V為通電定子電極上施加的非零電壓。利用式(3)和式(10)以及虛功原理，靜電電機轉(zhuǎn)子的輸出力矩可表示:

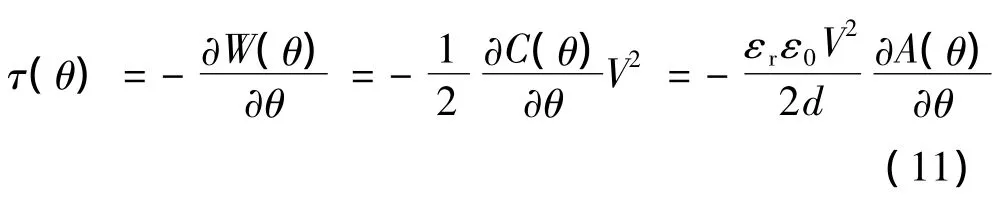
對于頂面驅(qū)動靜電微電機，由于電機定子和轉(zhuǎn)子形成的平板電容只隨兩極板間重疊面積A(θ)變化，而A(θ)只是轉(zhuǎn)子位置θ的函數(shù)，因此式(11)可表示為常微分形式:

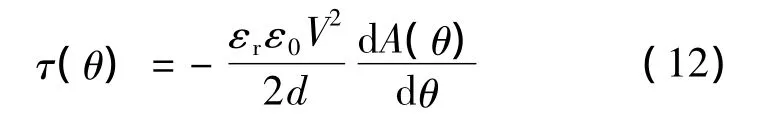
2 頂面驅(qū)動靜電微電機的驅(qū)動方式

當電機采用對稱單極控制方式時(這種控制方式的示意圖如圖2所示)，對于8/6可變電容靜電微電機，采用表1所示的電機參數(shù)［8］。

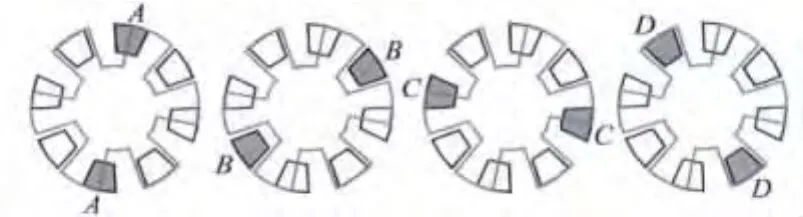
圖2 對稱單極控制方式

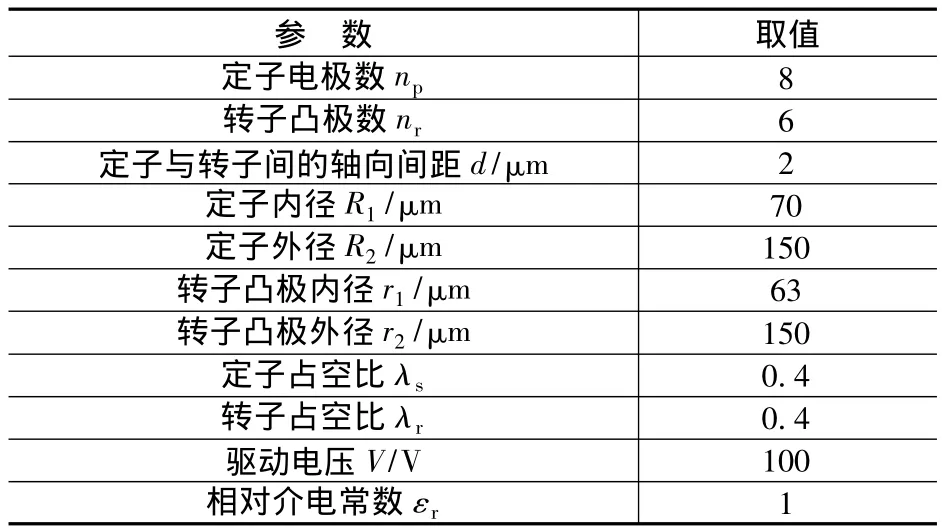
表1 頂面驅(qū)動8/6可變電容式靜電微電機的物理參數(shù)

當不同電極組分別通電時，轉(zhuǎn)子在轉(zhuǎn)動一個凸極位置過程中，轉(zhuǎn)子的輸出力矩與轉(zhuǎn)子位置的對應關系如圖3所示。通過適當切換通電電極組，可得如圖4所示的單向輸出扭矩，其平均輸出力矩為3.5679×10－10N·m。

圖3 對稱單極控制方式下的電機輸出力矩

圖4 對稱單極控制方式下的電機單向最大輸出力矩

為了增大電機的輸出力矩，本文采用對稱相鄰雙電極并聯(lián)控制方式(如圖5所示)，即在任意時刻只有兩對相鄰的定子電極通電，轉(zhuǎn)子上可獲得的輸出扭矩如圖6所示。在轉(zhuǎn)子轉(zhuǎn)動過程中，通過切換通電定子電極，且每次只切換第一組電極，則可獲得如圖7所示的單向最大輸出扭矩。在這種控制方式下，輸出扭矩的均值為4.5274×10－10N·m，比單極驅(qū)動下的平均力矩增大26.89%，但電機輸出扭矩的波動較大，這將使電機的負載能力下降。

圖5 對稱相鄰雙極控制方式

圖6 對稱相鄰雙極控制方式下的電機輸出力矩

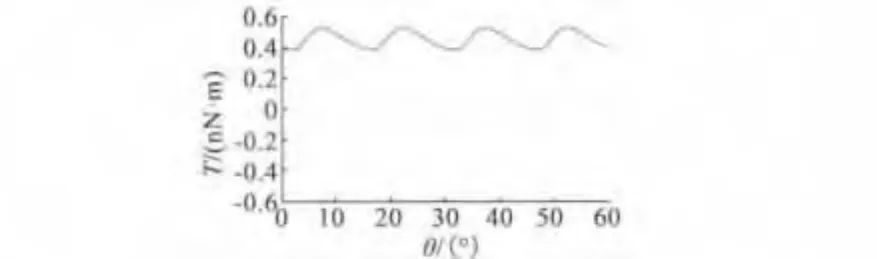
圖7 對稱相鄰雙極控制方式下的電機最大輸出力矩

3 電機結(jié)構(gòu)參數(shù)的優(yōu)化設計

這里考慮采用優(yōu)化設計方法改善電機性能，選擇優(yōu)化設計變量:

式中:λs和λr分別為定子電極、轉(zhuǎn)子凸極的占空比。電機的輸出力矩均值可表示:

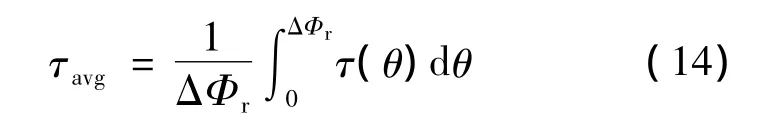
輸出力矩的波動系數(shù)表示:

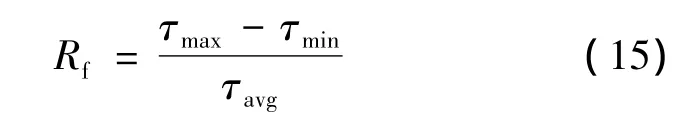
在優(yōu)化電機的結(jié)構(gòu)參數(shù)中，定義三種優(yōu)化指標，分別:

式中:z1用于優(yōu)化電機輸出力矩;z2用于優(yōu)化輸出力矩波動。式(18)中，λ為加權(quán)系數(shù)，可以調(diào)整z1和z2的數(shù)值為同一量級。基于式(16)～式(18)，可建立優(yōu)化問題的數(shù)學模型:

針對這種相鄰雙極并聯(lián)驅(qū)動控制方式，并基于表1中給出的電機基本參數(shù)，采用指標(18)并求解式(19)的優(yōu)化問題，對靜電電機的輸出平均力矩和力矩波動系數(shù)同時進行優(yōu)化。

由于在第1節(jié)給出的可變電容靜電微電機的數(shù)學模型不能獲得解析表達式，解析求解式(12)表示的電機輸出力矩很難實現(xiàn)，相應地，采用基于梯度或靈敏度分析的優(yōu)化方法難以實現(xiàn);這里采用遺傳優(yōu)化算法［9］。這種優(yōu)化方法對優(yōu)化問題的數(shù)學模型沒有特殊要求，它采用交叉、復制、變異三種簡單計算方法，能實現(xiàn)復雜空間中優(yōu)化問題的求解，并能獲得全局近似最優(yōu)解。由于采用了數(shù)值積分方法計算式(9)給出的電容極板重疊面積，并采用有限差分方法計算式(11)表示的電機輸出力矩，即使采用遺傳算法這種比較耗時的優(yōu)化方法，求解優(yōu)化問題(19)時也有較快的速度。

4 實驗結(jié)果

采用遺傳算法，對設計參數(shù)進行優(yōu)化后，電機定子電極和轉(zhuǎn)子凸極的占空比取值變?yōu)?λs，λr)=(0.348，0.501)，對應的輸出力矩如圖8所示。

圖8 相鄰雙極并聯(lián)控制方式下，8/6電機結(jié)構(gòu)參數(shù)優(yōu)化后的輸出力矩曲線

優(yōu)化前后電機輸出力矩如圖9所示:優(yōu)化后電機輸出力矩均值變?yōu)?.0821×10－10N·m，比優(yōu)化前減小9.84%，但是輸出力矩的波動系數(shù)從33.04%降為9.41%。

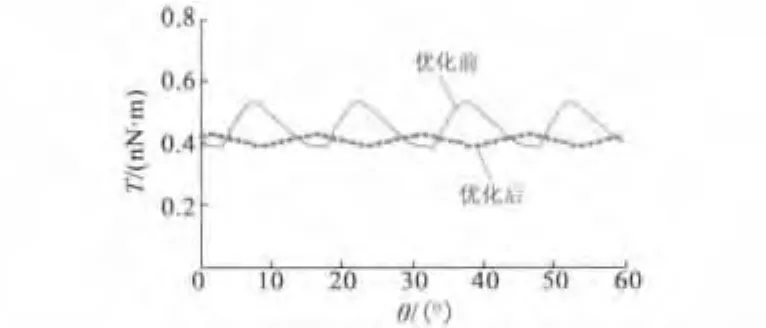
圖9 優(yōu)化前后8/6電機最大輸出力矩的比較

5 結(jié) 語

本文針對頂面驅(qū)動可變電容靜電微電機進行了優(yōu)化設計，建立了其一般解析物理描述模型。以8/6靜電微電機為例，進行了控制方式的優(yōu)化，并采用數(shù)值積分方法和遺傳優(yōu)化算法相結(jié)合的算法對電機進行了結(jié)構(gòu)參數(shù)優(yōu)化，不但使電機的輸出力矩明顯增大，而且有效降低了它的波動，從而改善了電機的性能。這種優(yōu)化設計方法，能快速進行頂面驅(qū)動可變電容靜電微電機的優(yōu)化設計，也更適合在MEMCAD等計算機輔助優(yōu)化設計軟件中應用。

［1］BACHMANN D，HIEROLD C.Determination of the pull－ off forces and pull－off dynamics of an electrostatically actuated silicon disk［J］.IEEE Journal of Microelectromechanical Systems，2008，17(3):643 －652.

［2］JUDY J W.Microelectromechanical systems(MEMS):fabrication，design and applications［J］.Smart Materials and Structures，2001，10(6):1115－1134.

［3］REBELLO K J.Applications of MEMS in Surgery［J］.Proceeding of the IEEE，2004，92(1):43 －55.

［4］LASER D J，SATIGO J G.A review of micropump［J］.Journal of Micromech.Microeng.，2004，14(6):35 －64.

［5］MEHREGANY M，TAI Y C.Surface micromachined mechanisms and micromotors［J］.Journal of Micromechanics and Microengineering，1991，1:73 －85.

［6］KETABI A，NAVARDI M J.Optimization of variable － capacitance micromotor using genetic algorithm［J］.Journal of Microelectromechanical Systems，2011，20(2):497 －504.

［7］BEHJAT V，VAHEDI A.Study the influence of geometric parameters on the torque of electrostatic micromotors［J］.Electrical Engineering，2006，89(1):61 －65.

［8］劉曉偉，何廣平.可變電容靜電型超微電機的優(yōu)化設計［J］.微特電機，2012，40(12):48 －52.

［9］QUAGLIARELLA D，PERIAUX P，POLONI C，et al.Genetic algorithms and evolution strategy in engineering and computer science［M］.New York:John Wiley＆ Sons，1998.