一種新的區域圖像插值算法*

余俊榮， 何彥行， 潘 豐

(江南大學 輕工過程先進控制教育部重點實驗室，江蘇 無錫 214122)

0 引 言

傳統的圖像插值算法有最臨近插值法、雙線性插值法和三次卷積插值法3種，但這3種算法分別存在灰度不連續、輪廓模糊、計算量大等問題。為了提高插值后的圖像質量或降低運算時間，國內外學者提出了很多改進的插值方法，主要概括為以下4類：1)基于低分辨圖像邊緣的插值算法[1～3]：其原理是首先檢測低分辨率圖像的邊緣，然后根據檢測的邊緣將像素分類處理，對于平坦區域的像素采用傳統方法插值，對于邊緣區域的像素，設計特殊插值方法。這類算法雖然提高了圖像的邊緣清晰度，但存在邊緣偏離的現象，放大倍數越大，偏離越嚴重；2) 基于高分辨圖像邊緣的插值算法[4～6]：此類算法首先采用傳統方法插值低分辨率圖像，然后檢測高分辨率圖像的邊緣，最后對邊緣和附近像素進行特殊處理，以去除模糊，增強圖像的邊緣。該算法可提高傳統方法的邊緣對比度，得到較好的主觀視覺效果，但由于對圖像進行了濾波處理，會導致圖像客觀質量有一定下降；3)基于邊緣保持的自適應插值算法[7～9]：這類算法能有效地去除圖像的鋸齒效果，但對小面積重復區域處理不足；4)基于區域的插值算法：插值原理是首先將原始低分辨率圖像依據不同方法劃分成不同區域，然后將插值點映射到低分辨率圖像，判斷其所屬區域，最后根據插值點的鄰域像素設計不同的插值公式，計算插值點的值。此類算法無論從主觀上還是客觀上，圖像質量均較好，但文獻[10]由于引入了圖像分割的方法，算法復雜度加大。

針對已有算法的一些不足，以第四類算法為指導，本文提出了一種新的區域方法用于插值算法中。該算法主要思路為先將待插值圖像等分成M×N個方格，分別計算方格4個端點的灰度均方差σ，并將σ與閾值T作比較從而判定方格屬于平坦區域還是紋理復雜區域；然后對紋理屬性相同的相鄰方格進行融合，進而完成整體的區域劃分；最后，根據待插值的點在源圖像中所屬的區域對應地選擇最佳插值算法。

1 圖像插值區域的劃分

1.1 區域概念提出的緣由

傳統的插值算法是對整幅圖像的像素均進行同樣的插值計算，沒有考慮圖像的局部特性，而圖像一般都有相對平坦區域和紋理細節豐富的區域。在平坦區域圖像灰度值變化很小，這時采用復雜的插值算法與簡單的插值算法相比，插值效果相當，但運算量增加很大；在紋理細節豐富的區域采用復雜的插值算法，則可以得到更高質量的插值效果。因而，在圖像的平坦區域采用運算量小的插值算法，在紋理細節復雜的區域采用三次卷積插值，就可以在保持插值后圖像質量的同時，減小計算量，降低運算時間[10]。以上便是插值區域這一概念提出的由來。

1.2 新的區域劃分方法

本文在綜合考慮了相關區域劃分方法存在的一些問題后，提出了一種具有廣泛適用性的新的區域劃分方法。

下面對一幅待插值圖像如何進行區域劃分作具體說明：

1)首先以它4個端點中的其中1個端點作為X—Y坐標系的原點，然后在X和Y方向上將圖像分別進行M和N個等分，如此便得到M×N個方格。

2)很容易得到方格4個端點坐標處對應的灰度值f11,f12,f21,f22及其均值E，計算這4個灰度值的均方差σ，即

σ=

(1)

均方差σ反映了一個方格其4個端點灰度值的離散程度，很明顯，σ數值越小，4個端點之間的灰度值跳變就越小，也就表明其灰度紋理相對越平坦。

3)將σ與設定的閾值T作定量比較，如果σ小于T，則將整個方格歸為紋理平坦區域(下文均用A表示)；否則，歸為紋理復雜區域(下文均用B表示)，圖1為初步劃分好的區域示意圖。

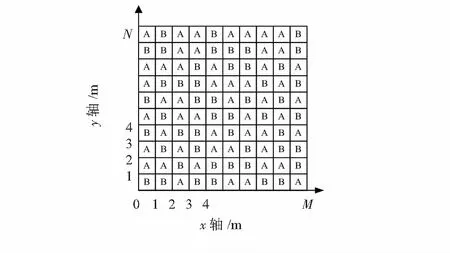
圖1 初步區域劃分示意圖

4)經步驟(3)劃分后的圖像，如果存在圖1所示的AA(或BB)相鄰，則將該區域融合，形成新的區域A(或B)，如此作進一步的區域劃分，如圖2所示。

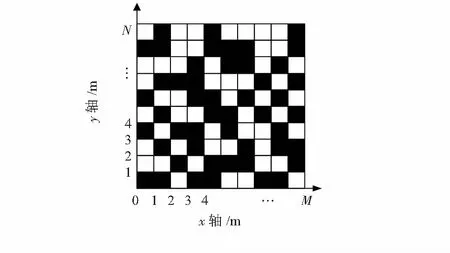
圖2 區域劃分最終效果圖

為了使示意圖像效果對比更明顯，這里把屬于區域A的用白色填充，屬于區域B的則用黑色填充。

完成上述步驟后，對待插值圖像的區域劃分便實現了。

1.3 關鍵參數的確定

本文劃分方法中有2組關鍵參數選取尤為重要：

1)M,N的選取：很顯然M,N的值越大，圖像劃分越細，但同時無可避免地也帶來了更大的計算量。那么如何選取M，N的值呢？一幅圖像是由很多像素組成的，比如：已知一幅圖像的分辨率為640像素×480像素，可以得出：這幅圖像水平方向有640個像素，垂直方向有480個像素，整幅圖像含有640像素×480像素。基于該理論知識，在設計方格大小時，便可以根據實際需要自行設定一個方格水平和垂直方向含有的像素個數，從而得到M，N的值，即

(2)

其中，Lf,Df分別為圖像分辨率的水平像素和垂直像素，α為像素的個數，其數值可以自行定義。至此，M，N的取值并沒有真正解決，對α取多少合適，業內在初評估一個檢測項目能否達到檢測精度要求時，通常會采用10像素偏差法來進行評估，即綜合考慮硬件誤差、軟件工具誤差和人為誤差后，如果系統偏差10個像素或以上時，系統還能達到所需要的檢測精度，該檢測系統是穩定可行的。舉例說明：已知一個檢測系統，視野范圍為64 mm×48 mm，檢測精度要求達到0.4 mm/pixel，如果采用200萬像素(分辨率為1 600像素×1 200像素)的工業相機能否達到檢測要求？答案是可行的，已知分辨率和視野范圍，那么可以很容易得到該檢測系統的像素精度P=64 mm/1 600 pixel=0.04 mm/像素(寬邊求取結果一樣)。

顯然，該檢測系統即使偏差10個像素，其檢測精度仍能達到0.4 mm/pixel。從上述舉例可以看出：一旦一個檢測系統確定以后，其獲取的圖像在后期處理時即使有10像素的偏差，也是允許的。基于該準則，本文圖像作區域劃分時，α的值均取10。

事實上，對圖像區域進行劃分時，α值的大小不會破壞圖像已有的像素精度，本文之所以這樣做，只是提供了一種確定M，N值大小的方法，使其在一定程度上更具規范性，并盡量降低后期處理時可能帶來的誤差。在實際應用中可以根據需要進行一個大小的調整，但α值顯然不易過大，否則，會導致步驟(3)中劃分的區域沒有更多的區分度。

2)閾值T的選取：在圖像分割中，也會經常涉及閾值的問題，但其最佳閾值通常都能通過分割算法自行算出，如迭代法和Ostu算法[11]。本文出于計算運行量的考慮，對區域劃分時沒有引入圖像分割的算法，但同時也帶來了一個問題，就是對步驟(3)中的閾值T如何選取。本文從公式(1)著手，對其作簡化處理如下

t=(f11-E)2+(f12-E)2+(f21-E)2+(f22-E)2.

(3)

定義方格4個端點兩兩之間的灰度差為Δf，那么,可以得到如下關系式

(4)

將

(5)

代入式(3)，并結合式(4)，整理得

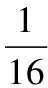
(Δf2+Δf4-Δf6)2+(Δf3+Δf5+Δf6)2].

(6)

由式(4)可以推出

(7)

代入式(6)，得到一個只關于Δf1,Δf2,Δf3的方程，化簡整理后即為

(8)

對式(8)作進一步處理，可以得到式(9)

t=

(9)

再結合式(7)，有

(10)

一個區域如果紋理相對平坦，其4個端點兩兩之間的灰度差Δf應該滿足如下關系式

-p≤Δfi≤p,i∈[1,2,…,6].

(11)

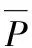
(12)

根據式(11)，結合式(12)，可以由式(10)推導得到t的如下關系式

(13)

結合式(1)，從而得到T的定量公式

(14)

顯然n越大，閾值越小，對區域的劃分越細，但為了兼顧算法的運算量，建議n取20較為合適，本文對圖像進行處理時均采用n=20。

1.4 區域條件下的插值算法

完成區域劃分后，就可以進入圖像插值的階段。由于本文采用方格對區域進行劃分，所獲得區域分屬也只是相對而言。因此，如果待插值的點屬于區域A，為了保證圖像擁有足夠的插值精度，那么選用精度高的雙線性插值算法而不采用精度較差的最鄰近插值算法；如果待插值的點屬于區域B或在AB區域的交界線上，那么選用最高精度的三次卷積插值算法。本文完整的算法流程圖如圖3。

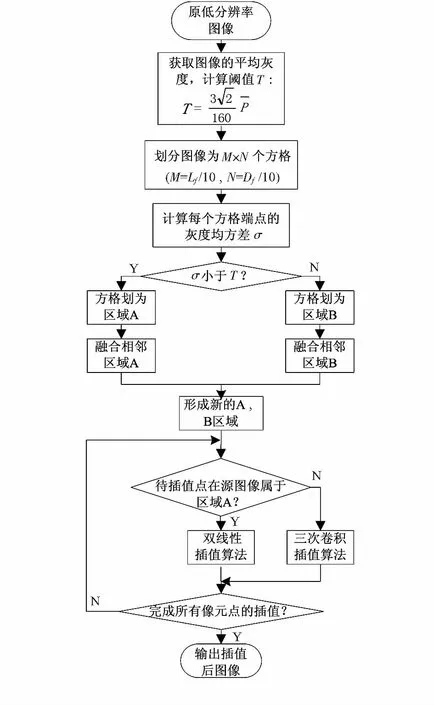
圖3 算法流程圖

2 仿真結果與分析

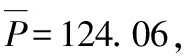
圖4 Lena仿真結果

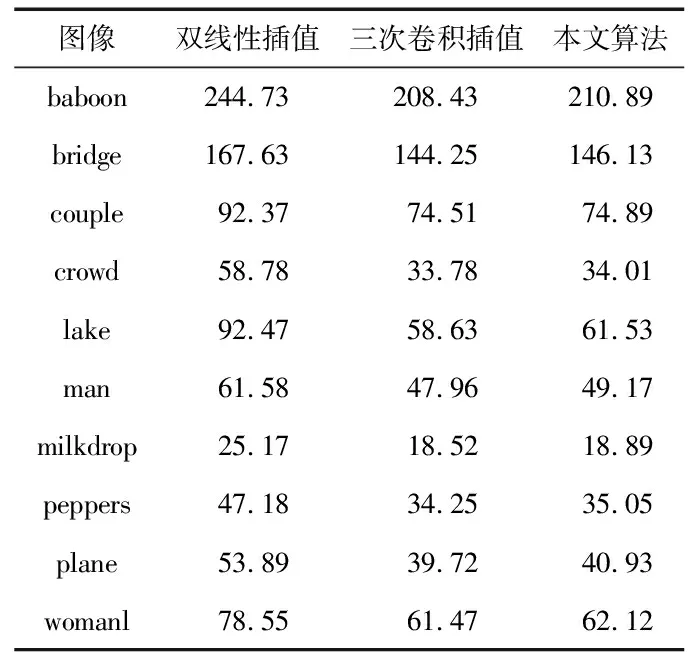
表1 不同算法的均方誤差

從表1中可以得出:本文算法插值后獲得的圖像質量，與三次卷積插值非常接近。算法運算時間方面，由于雙線性插值和三次卷積插值均是對整幅圖像進行插值，因此，運算時間與圖像內容無關，均在200，380 ms左右，而本文的運算時間如表2所示。

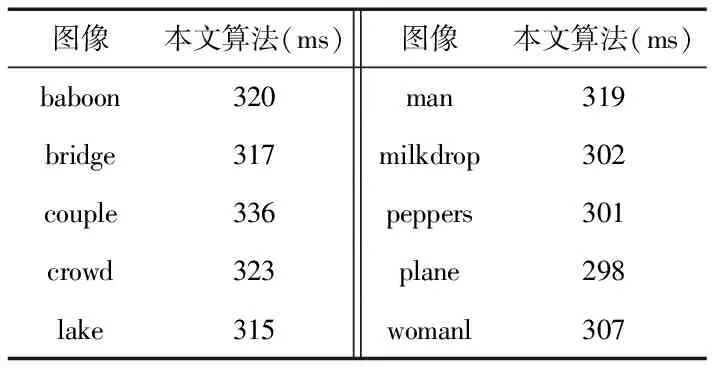
表2 算法運算時間

從表2中可以算出:本文算法的平均用時為314 ms，與三次卷積插值相比運算時間降低了17.4 %。

3 結束語

本文提出了一種新的區域劃分插值算法，在保持圖像質量的同時，一定程度上降低算法運算時間。另外，本文閾值T可以根據不同的圖像進行自動調整，具有普遍適用性。仿真實驗結果表明:本文算法具有較高的插值精度，圖像質量逼近三次卷積插值算法，而運行時間降低了約17.4 %。

參考文獻:

[1] 張 雄,畢篤彥,楊寶強.一種保持圖像邊緣的插值方法[J].空軍工程大學學報,2007,8(3):78-80.

[2] Li X,Orchard T.New edge-directed interpolation[J].IEEE Trans on Image Processing,2001,10(10):1521-1527.

[3] 劉政林，肖建平，鄒雪城，等.基于邊緣的實時圖像縮放算法研究[J].中國圖像圖形學報,2008,13(2)：225-229.

[4] 黨向盈,吳錫生,趙 勇.基于邊緣最大梯度的多方向優化插值算法[J].計算機應用研究,2007,24(9):317-320.

[5] Wang Q,Ward R,Zou J C.Contrast enhancement for enlarged images based on edge sharpening[C]∥Proceeding of IEEE International Conference on Image Processing,Genova: IEEE,2005:762-765.

[6] 高 嵐,方康玲,付 旭,等.一種邊緣保護的灰度圖像插值算法[J].武漢科技大學學報,2004,27(2):188-190.

[7] Mishiba K，Suzuki T,Ikehara M.Edge-adaptive image interpolation using constrained least squares[C]∥Proc of the 17th IEEE International Conference on Image Processing,2010:2837-2840.

[8] Caseiola G，Montefuseo L B,Morigi S.Edge driven image interpolation using adaptive anisotropic radial basis functions[J].Journal of Mathematical Imaging and Vision,2010,36(2):125-139.

[9] Ratner V,Zeevi Y Y.Denoising-enhaneing images on elastic[J].IEEE Trans on Image Processing,2011,20(8):2099-2109.

[10] 符 祥,郭寶龍.區域指導的自適應圖像插值算法[J].光電子·激光,2008,19(2):233-236.

[11] 肖 剛,應曉芳,高 飛,等.基于鄰域灰度差值的二維Otsu分割方法研究[J].計算機應用研究,2009,26(4):1544-1548.

[12] 陳 超.Matlab應用案例精講[M].北京:電子工業出版社,2011.