基于RSSI距離修正的WSNs定位算法*
王佩琦, 李艷萍, 陳相南, 李 婧
(太原理工大學 信息工程學院,山西 太原 030024)
0 引 言
隨著物聯網技術的快速發展,無線傳感器網絡(wireless sensor networks,WSNs)技術得到了廣泛的應用[1~3]。在WSNs中,節點位置信息的確定是WSNs技術的重要環節,節點定位算法的設計已成為目前WSNs的研究熱點。
現有的定位方法從定位手段上分為基于測距(range-based)和無需測距[4](range-free)兩大類。基于測距的方法需要節點有測距功能,利用節點間的實際距離或角度信息,使用三邊定位、三角定位或極大似然估計等定位算法計算節點位置。常用的測距技術有超聲波、紅外線、GPS和接收信號強度指示(received signal strength indicator,RSSI)等。其中,RSSI測距技術根據對接收信號強度的判斷,計算出收發節點間的距離,由于對硬件要求較少,所以,它成為無線定位技術的首選[5]。文獻[6,7]提出了采用修正RSSI權系數的方法優化定位算法。
三邊定位技術[8,9]由于算法簡單,大量應用于無線定位系統中,其基本原理是由未知節點測得與周圍3個坐標已知的錨節點的距離,分別作為3個錨圓的半徑,在理想情況下,3個圓交于一點,通過幾何計算可以得到未知節點坐標。但在實際應用中,由于存在噪聲干擾,致使3個圓不能相交于一點,導致定位精度下降甚至定位失敗。文獻[10]通過分析錨節點之間的通信約束和幾何關系,提出一種錨圓交點的加權質心定位算法,減小定位誤差。
本文提出了RSSI距離補償機制算法,在錨圓不相交的情況下能夠準確進行節點定位,提高在噪聲環境中的定位性能。
1 RSSI測距模型
無線信號傳播模型主要有自由空間傳播模型、雙徑地面反射模型和Shadowing模型等,目前普遍采用的是Sha-dowing模型,該模型為[11]
(1)
其中,RSSId為接收到的信號強度;d為收發端的實際距離;d0為參考距離;RSSId0是距離為d0時的信號強度;n為信道衰減指數,由傳輸環境決定;Xσ是方差為σ、均值為0的高斯隨機變量。在實際的測量中,不考慮Xσ,采用以下的模型
RSSI=-(10nlgd+A),
(2)
式中A為距發射節點1 m 處的接收信號強度,dBm。
2 RSSI距離修正算法
2.1 算法原理
在圖1中,3個錨節點A1,A2,A3是未知節點附近RSSI值最強的3個點,具有最大的參考價值,但是它們的圓不相交,現將RSSI值最強的錨節點A1稱為靶節點,RSSI距離修正的原理是:將圓A2,A3的半徑分別增加一定距離,使三個圓兩兩相交,形成一個重疊區域,如圖1陰影部分所示。再通過加權質心算法求得未知節點坐標。增加后的半徑r2和r3由式(3)求得
(3)
其中,r1為靶節點的半徑;d1,2為A1,A2間的距離;d1,3為A1,A3間的距離。
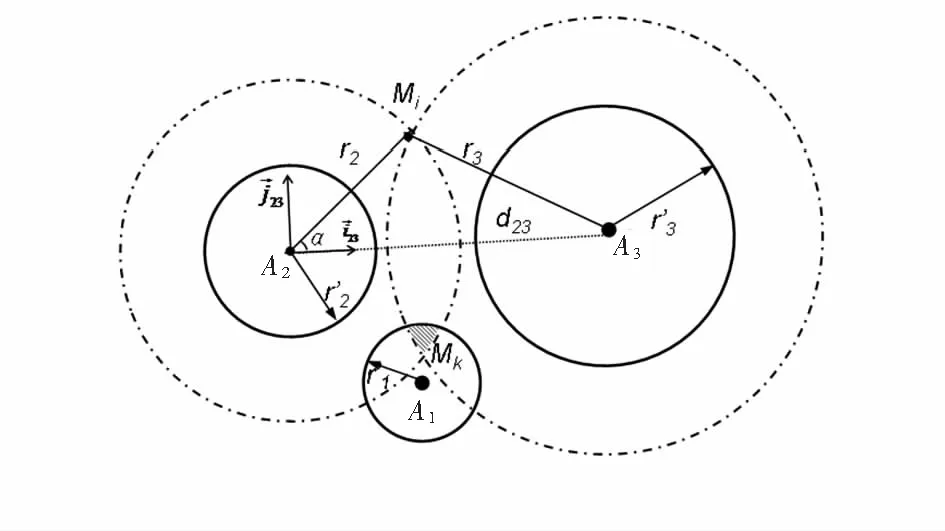
圖1 算法原理圖
兩圓交點Mi,Mk坐標,可以通過兩錨節點A2,A3間的距離d2,3和兩錨節點的坐標(x2,y2)(x3,y3)計算得出,具體方法如下:
首先求得A2,A3之間的距離d2,3為
(4)
線段A2A3與線段A2Mi的夾角α為
(5)
(6)

(7)
最后,求Mi,Mk坐標為
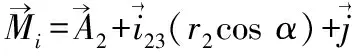

(8)
2.2 定位過程
現在對采用RSSI距離修正定位的整個過程進行分析:
1)首先,未知節點向周圍發送定位請求,錨節點收到定位請求信息后,向未知節點發送含有自己坐標和RSSI值等信息的回傳數據包;然后,未知節點根據收到的回傳信息計算與各錨節點的距離r1,r2,r3,…;
2)用冒泡排序法將錨節點與未知節點的距離進行排序,使r1 3)判斷A1,A2是否相交,如果不相交,則根據式(3)算出修正量來擴大A2的半徑,使兩圓交于點M1,M2; 4)如果M1,M2有一點超出了實際定位區域的范圍,則舍去該點,另一點設為p1,并將標志位Flag置0;如果兩點都在范圍內,則暫時將M1,M2中點設為p1,標志位Flag置1; 5)判斷A1,A3是否相交,如果不相交,則擴大A3的半徑,與A1相交于M3,M4兩點,并將其中靠近p1的點設為p2; 7)當標志位Flag為1時,將M1,M2中靠近p2的點重新設為p1。 此時未知節點的位置就在p1,p2,p3構成的區域內,如圖2陰影部分所示。根據p1,p2,p3三個點的坐標(xp1,yp1),(xp2,yp2),(xp3,yp3)通過加權質心算法[12]可求得未知節點的坐標 (9) 其中,權值為:w1=1/d1,w2=1/d2,w3=1/d3。 圖2 錨圓相交區域 為了得到RSSI和距離的關系,在6 m×10 m的教室進行了2個節點的通信實驗,節點采用基于Zig Bee的CC2530模塊,一個用來接收信號,一個用來發送信號,節點高度定為1.5 m,節點發射功率為1 mW。每一個測量點距發射點的距離在0.1~5 m內變化,每次增加0.1 m,記錄200個收到的數據包,RSSI距離關系如圖3所示,通過對數據擬合得到RSSI距離關系 RSSI=-18lgd-34. (10) 圖3 RSSI與距離的關系 實驗在教室進行,采用12個錨節點和1個未知節點以及1個網關節點,未知節點將定位信息傳給網關節點。 圖4 現場實驗布局 錨節點間相隔3 m呈網格狀分布,如圖4所示。未知節點依次經過10個指定位置時,記錄25次定位點的坐標,然后計算定位誤差,定義定位誤差為 (11) 其中,(x,y)為計算得到的未知節點的位置,(xe,ye)為其真實位置。誤差的最大值、最小值以及平均值如表1所示。 表1 實驗結果 從表1的數據可以得出平均誤差為0.62 m,并且離錨節點近的位置誤差較小,表明RSSI距離修正算法在定位時,RSSI值大的錨節點對定位的影響較大。 為了分析在錨節點隨機分布的情況下算法的性能,采用Matlab進行仿真實驗,將20個錨節點和6個未知節點隨機分布在6 m×10 m的區域內,分布情況如圖5所示。仿真使用2種定位算法,另一種是極大似然法,并對定位誤差進行分析比較,分析結果如圖6所示。仿真結果表明:RSSI距離修正算法的定位誤差小于極大似然算法,定位精度更加精確。 圖5 節點分布情況 圖6 仿真結果 本文提出一種RSSI距離修正算法,通過調整錨節點的定位圓半徑,再結合加權質心法,彌補了錨圓不能相交時對未知節點定位造成的誤差。現場實驗和仿真分析表明:RSSI距離修正算法在節點指定分布和隨機分布的情況下都表現出較高的定位的精度,較好的定位性能,可以很好地應用于室內定位等領域。 參考文獻: [1] 孫利民,李建中,陳 渝,等.無線傳感器網絡[M].北京:清華大學出版社,2005. [2] Lazarescu M T.Design of a WSNs platform for long-term environmental monitoring for IoT applications[J].IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2013,3(1):45-54. [3] Blumrosen G,Hod B,Anker T,et al.Enhanced calibration technique for RSSI-based ranging in body area networks[J].Ad Hoc Networks,2013,11(1):555-569. [4] 丁恩杰,喬 欣,常 飛,等.基于RSSI的WSNs加權質心定位算法的改進[J].傳感器與微系統,2013,32(7):53-56. [5] 譚 志,張 卉.無線傳感器網絡RSSI定位算法的研究與改進[J].北京郵電大學學報,2013,36(3):88-91. [6] 趙 昭,陳小惠.無線傳感器網絡中基于RSSI的改進定位算法[J].傳感技術學報,2009,22(3):391-394. [7] 張治斌,徐小玲,閻連龍.基于Zig Bee井下無線傳感器網絡的定位方法[J].煤炭學報,2009,34(1):125-128. [8] Han Guangjie,Choi D,Lim W.Reference node placement and selection algorithm based on trilateration for indoor sensor network-s[J].Wireless Communications and Mobile Computing,2009,9(8):1017-1027. [9] Yang Zheng,Liu Yunhao.Quality of trilateration:Confidence-based iterative localization[J].IEEE Transactions on Parallel and Distributed Systems,2010,21(5):631-640. [10] 李 娟,王 珂,李 莉,等.基于錨圓交點加權質心的無線傳感器網絡定位算法[J].吉林大學學報:工學版,2009,39(6):1649-1653. [11] 朱明輝,張會清.基于 RSSI 的室內測距模型的研究[J].傳感器與微系統,2010,29(8):19-22. [12] 張嬋愛,馬艷艷,白鳳娥,等.基于RSSI的加權質心定位算法的實現[J].太原理工大學學報,2009,40(2):146-147.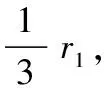
3 實驗與結果分析
3.1 建立測距模型
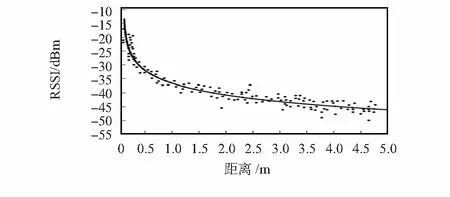
3.2 現場試驗
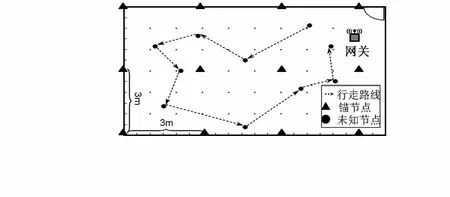
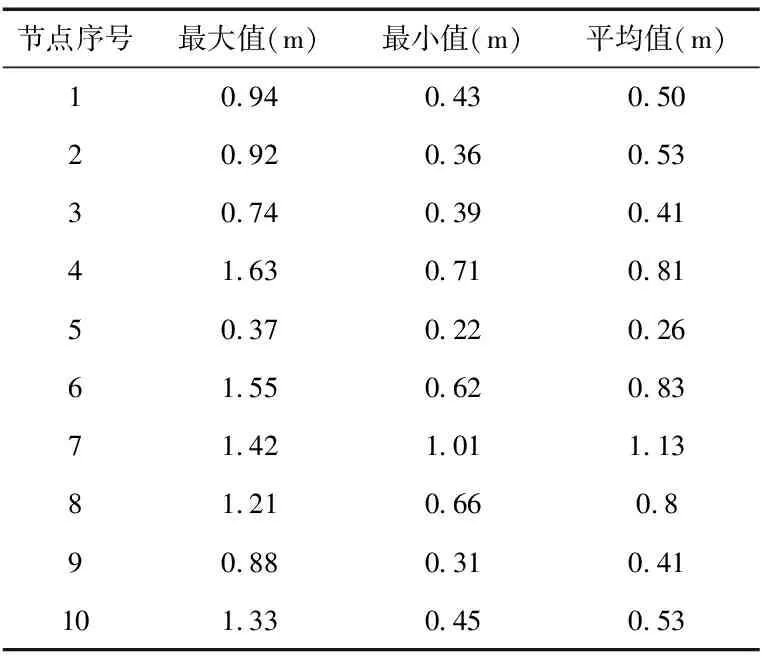
3.3 仿真分析

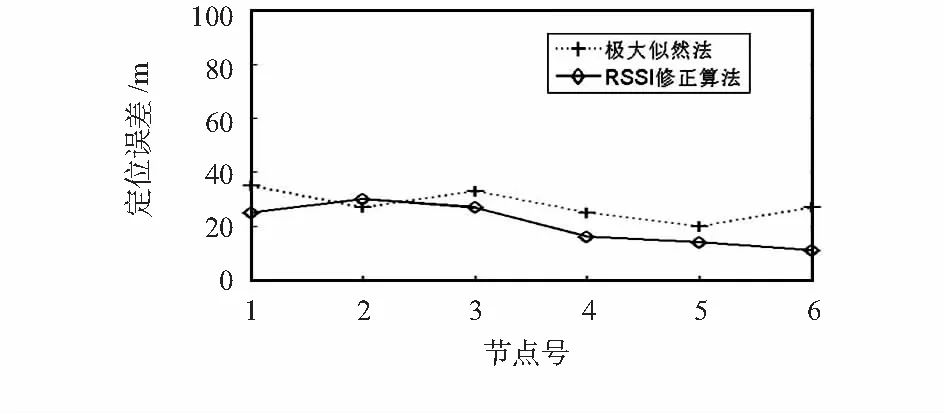
4 結束語

