基于優選幾何分組增強的假設檢驗RAIM方法*

賀 劉， 崔曉偉， 陸明泉

(清華大學 電子工程系, 北京 100084)

0 引 言

隨著全球導航定位系統的建設與發展，雙模甚至多模系統聯合導航將成為未來導航的主要應用方式[1]。聯合導航系統帶來了大量測距資源，更優的衛星分布幾何結構為定位估計精度的提升帶來契機。而可見衛星測距資源的倍增客觀上增大了測距出現故障的概率，電離層突變、城市中大量多徑干擾、人為的干擾以及欺騙都將對測距置信度帶來挑戰[2]。因此，聯合導航系統的完好性被廣泛關注，重要性日趨凸顯。接收機自主完好性監測(receiver autonomous integrity monitoring，RAIM)算法能夠對可見測距實時、有效監測，具有結構簡單、處理迅速的特點，是用戶端廣泛使用的完好性算法。通過故障檢測與排除(fault detection and exclusion，FDE)步驟剔除故障測距，利用冗余信息提高測距置信度，以保證定位解的完好性。傳統RAIM算法對較大故障檢測排除率高，而對城市多徑等原因易引起的大量15～50 m級(約3σ～10σ，σ為系統測距標準差)較小故障偏差，易出現漏檢現象。為保證定位精度，能有效識別較小測距故障并支持多測距故障場景成為新形勢下RAIM技術的難點。

基于此，本文通過建立衛星分布幾何結構與定位估計、故障檢測關系模型，通過研究各模型衛星分布幾何結構對故障測距引起的定位誤差與檢測統計值間耦合性的影響。在假設檢驗方法基礎上，提出了基于幾何優選分組增強的接收機完好性方法，以解決新形勢下RAIM技術難題，增強聯合導航接收機自主完好性性能水平。

1 聯合導航系統RAIM方法

1.1 聯合導航系統最小二乘殘差RAIM算法

由定位解算觀測模型[1]

Y=HX+E,

(1)

式中X為待求接收機坐標與m個鐘差修正值，m為系統數，對GPS/Galileo雙模系統，m=2；Y為(n×1)維殘差向量；H為n×(3+m)維觀測矩陣；H矩陣最后m列依次對應各系統接收機鐘差，用1，0對應于該測距所屬系統。E為噪聲矢量。由式(1)可得到最小二乘估計解

(2)

偽距殘差矢量W是多模最小二乘殘差RAIM(簡稱LSR)算法的核心，表示偽距估計值與測量值之差，可由最小二乘解計算得到

W=Y-H=(In-H(HTH)-1HT)Y.

(3)

若令

S=In-H(HTH)-1HT.

(4)

由式(3)、式(4)易得

W=SY=SE.

(5)

由式(5)可知，無測距偏差時，W僅為噪聲的函數，而出現測距偏差時，W將由噪聲與偏差共同影響。檢測統計量SSE為

(6)

由于|W2|/σ0服從自由度為n-(3+m)的χ2分布,根據用戶給定的虛警概率Pfa，可以計算得到檢測閾值TD。比較SSE與TD的大小關系，以判斷是否存在故障測距。

1.2 假設檢驗RAIM算法

LSR算法由于檢測結構和判別準則不合理等原因，該算法僅支持單測距故障情況[3]，而假設檢驗法能夠支持多測距故障場景[4]。早期假設檢驗算法遍歷不含假設故障星的子集，加權計算垂向保護級別(VPL)值，找到對應最小VPL值的子集，該子集假設的故障星為故障測距。VPL由下式得出

(7)

由最壞假設條件準則，最大垂向特征斜率SLOPEmax最易出現故障。式(7)中λ為非中心χ2分布概率密度函數的非中心參數，可由如下積分確定

(8)

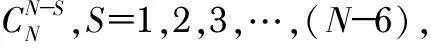
2 優選幾何分組增強RAIM方法

2.1 衛星分布幾何結構與定位估計、故障檢測關系模型

用戶提出虛警率需求后，RAIM算法的有效性主要取決于衛星分布幾何結構與冗余測距數量[6]。多系統倍增的可見測距使系統不再受冗余測距數限制，而衛星分布幾何結構成為影響RAIM有效性的重要因素。為研究衛星分布幾何結構與定位估計、故障檢測率關系，建立圖1模型，將 3維衛星用戶幾何結構簡化為2維，冗余度為1，至少需 3個測距。

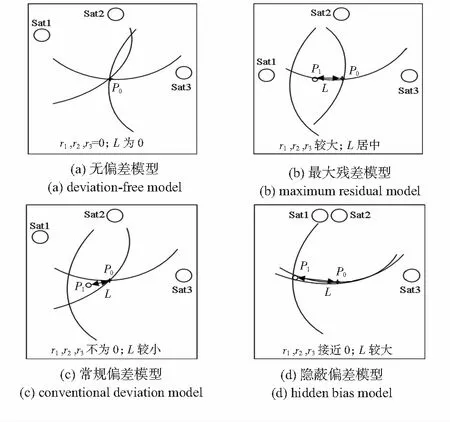
圖1 幾何結構、定位估計和故障檢測率關系模型

2.2 優選幾何分組增強RAIM方法

由建模可知，衛星分布幾何結構將影響故障測距映射在檢測統計量中統計值的大小，而較優幾何分布結構能夠使故障測距引起的定位誤差與觀測到的檢測統計值之間具有較大的耦合性。據此，形成了一種優選幾何分組增強RAIM方法的設計思路：在現有假設檢驗方法(改進后的假設檢驗方法，下同)基礎上，通過增加可能故障檢測范圍，結合較優幾何模型合理分組以隔離可能故障測距，經過復檢，以實現在仍保持較低復雜度，滿足單、多測距故障場景的基礎上，極小化故障漏檢，從而極大化較小測距的檢測排除性能，并能改善原方法易產生虛警的缺點。

由式(3)可知，偽距殘差的幅值能夠體現各測距觀測值的一致性，對n個可見測距，偽距殘差矢量WI為

WI=[w1,w2,…,wn]T.

(9)

將假設檢驗法排除的故障測距與殘差矢量WI中最大殘差矢量對應測距組成待校驗K子集。由建模分析可知，圖1(b)模型衛星分布幾何結構下故障測距偽距殘差值較大，使用LSR法不易產生漏檢，該幾何模型在DT-RAIM算法[7,8]中也取得了較優的檢測效果。現將該模型作為優選幾何模型，并對K子集各元素按照該模型構造優選分組。對于GPS/Galileo系統，冗余度為1，分組至少需6個測距。建立相應比較分組，由幾何優選模型確定的5個測距與K子集外 對應測距組成。各測距對應殘差矢量wi

(10)

式中xi,yi,hi分別為,Y,H矩陣中測距對應行。由式(3)、式(5)可得wi為

(11)

式中ei為E矢量對應行。由式(11)得到各測距wi，將分組間偽距殘差平方和之差作為檢測統計量FE

(12)

當存在測距偏差時

E=Enois+Ebias.

(13)

雙頻定位能夠消除大部分電離層延遲噪聲，則式(13)中Enois主要為熱噪聲，假設其服從期望為0，方差為σ0的正態分布。由于檢測閾值FD與噪聲量級相關，為概率統計值，不易量化估計，參考斯坦福大學提出的RANCO算法[3,6]，FD值與虛警率呈正比，應根據用戶需求調整，取σ的倍數。提出方法的具體步驟為：

1)計算可見星及其方位、俯仰角；

2)假設S顆故障星，循環檢測得到正常衛星組，每次檢測需按照冗余度計算SSE與TD；

3)構造待檢K子集，為兼顧虛警與復雜度，一般增加1個待檢測距；

4)對K子集元素構造優選幾何模型分組；

5)計算分組間檢測統計量FE；

6)判別是否存在測距偏差，若存在，排除該元素對應測距。

需注意：循環檢測時應避免某系統僅含1個測距的情況，若該測距出現測距偏差會被作為接收機鐘差計算，極易造成漏檢。

2.3 分組策略

分組策略依據星座中與待檢測測距180°對稱方向和90°正交方向均有正常測距的原則，各方向測距數量大致相當,可由下式確定

(14)

式中A,E分別為有效測距方位、俯仰角，角標0指待檢測距、i指其余可見測距。選擇5個最小(δ1+δ2),(δ1+δ3)值所對應測距，與待檢測測距組成優選分組。

設6號星為待檢測距，由式(14)得到圖2所示：優選幾何分組星空圖，衛星號為：17,9,4,1,15,6。容易看出:可見測距越多，分組測距與優選模型衛星分布幾何結構相符度越高，故障檢測排除性能將越好。

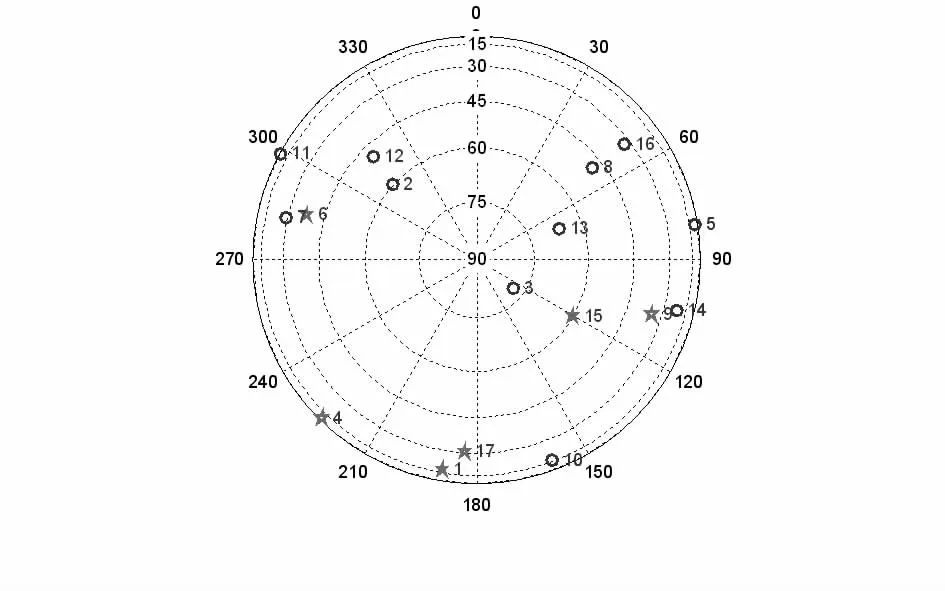
圖2 優選幾何分組星空圖

3 仿真驗證與分析

3.1 仿真環境

由軌道參數仿真GPS系統(24星星座)、Galileo系統(27星星座)衛星位置，并將2個系統數據歸一化。仿真時間為1天，采樣步長1 min，得到1 440個歷元，可見星遮蔽角為5°，地點為北京觀測站，σ統一為5 m[9]。

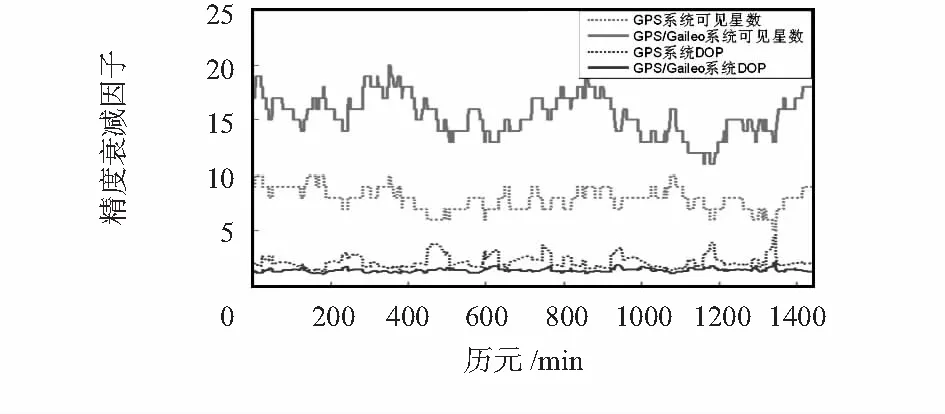
圖3 可見星數與精度衰減因子

聯合導航系統將帶來倍增的可見測距和更合理的星座幾何結構。由圖3可看出:GPS/Galileo系統可見星數為13～20顆，精度衰減因子(dilution of precision,DOP)值也明顯優于GPS單系統。

3.2 故障檢測和排除性能仿真測試

模擬單星斜坡故障場景檢測LSR法、假設檢驗法和本文方法的正確檢測和排除性能。隨機選取一個正常測距，添加以1σ為步長的測距偏差，由2σ增長至11σ。各方法虛警率Pfa為1×10-3，漏檢率Pmd為1×10-4。

圖4、圖5顯示了各方法故障檢測率、排除率和虛警率仿真結果。LSR法故障檢測率和排除率基本一致，對較小故障檢測率較低，但虛警率很小；假設檢驗法對較小故障仍不敏感，且在某些測距偏差的虛警率較高；本文方法有效避免了漏檢，與前2種方法相比，各級測距偏差的檢測和排除率均有一定提升，提前1σ達到100 %排除故障測距。

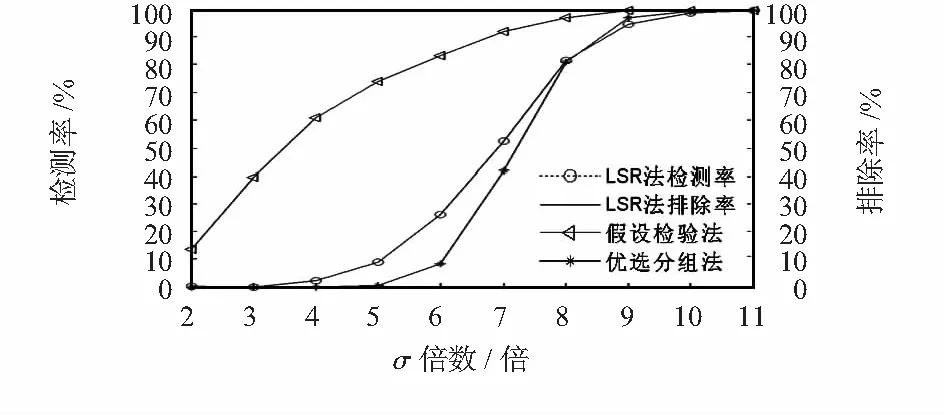
圖4 單測距故障檢測與排除率

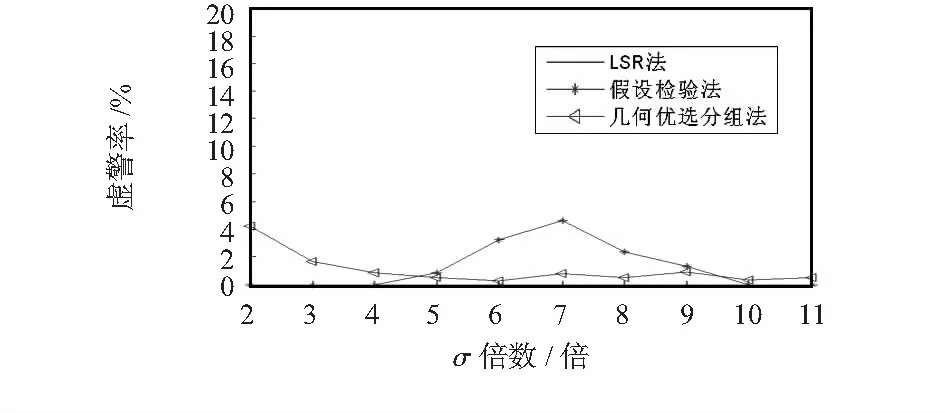
圖5 單測距故障虛警率

本文方法經過K子集的復檢，有效降低了假設檢驗法產生的虛警。在小于3σ時產生了一定虛警，是由于噪聲干擾和故障測距對其他正常測距的傳遞作用，使正常測距可能被其影響[7]所致。總體來看,本文方法的平均虛警率較小，且通過調整FD值可調節檢測率與虛警率均衡關系。

正確檢測率指能夠正確檢測到故障測距的概率，能夠體現RAIM算法有效性[8]。模擬雙斜坡故障場景，隨機選取2個正常測距，分別增加以0和3σ的測距偏差初始值，以σ為步長的斜坡故障。圖6顯示，本方法正確檢測率在各級誤差下均有所提升，10倍偏差時達到90 %。

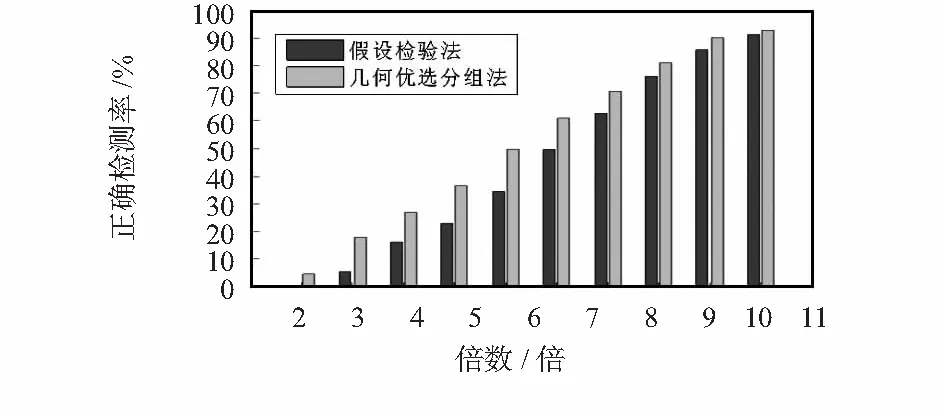
圖6 雙測距故障正確檢測率

3.3 告警時間與定位估計誤差

仿真各方法首次正確告警時間T，以檢驗各方法對測距偏差的敏感性。隨機選取1個正常測距，添加步長為1 m的斜坡故障，模擬1Sat故障場景；隨機添加2個1Sat故障模擬2Sat故障場景。通過2000次Monte Carlo仿真得到表1結果，Ai指首次檢測偏差值與σ之比。可以看出:本方法在各場景的告警時間更短，檢測出的偏差值更小，對較小測距故障更敏感。

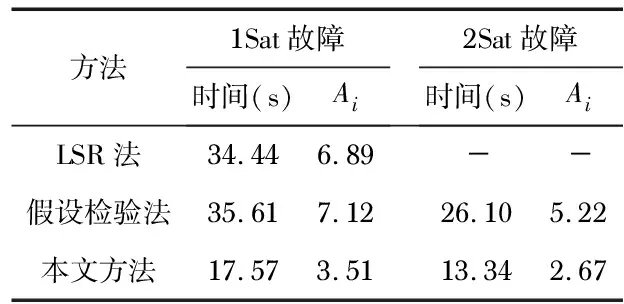
表1 斜坡故障首次告警時間

為模擬城市多徑干擾對定位估計解的影響[10]，隨機選取2個可見測距加入15～50 m突變偏差，由全天1 440采樣點仿真得到表2結果。可以看出，較小故障對聯合導航系統定位估計影響較大，未加RAIM時誤差達到12.67 m。由于本文方法的正確故障檢測和排除率高于假設檢驗方法，且虛警率更低，能夠提供置信度更高的可見測距。增加RAIM算法后，定位估計結果準確度提升明顯，誤差降為3.57 m。

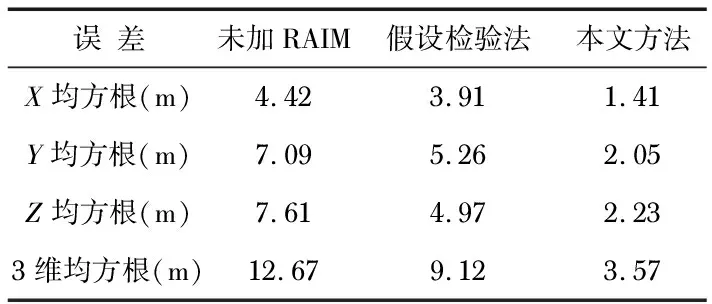
表2 雙測距故障定位誤差估計

4 結 論

本文通過建立典型衛星分布幾何結構模型，研究指出衛星優選幾何分組模型能夠增強故障測距引起的定位誤差與檢測統計值間耦合性的規律特點。進而在假設檢驗方法的基礎上，利用分組間殘差矢量關系建立新型檢測統計量與門限值，提出了一種基于幾何優選分組增強的接收機完好性方法，以滿足聯合導航系統聯合導航高置信度測距需求。仿真表明:該方法能夠有效提升較小故障檢測和排除率，支持聯合導航系統單、多測距故障場景假設，降低了定位估計誤差，可靠保證了定位估計精度。

參考文獻:

[1] 郭 婧.多模多頻衛星導航RAIM技術研究[D].北京：清華大學電子工程系，2011.

[2] Hwang P Y,Brown R G.RAIM-FDE revisited:A new breakthrough in availability performance with NIO-RAIM (Novel-Integrity-Optimized RAIM)[J].Navigation,2006,53(1):41-51.

[3] Schroth Georg,Rippl Markus,Ene Alexandru,et al.Enhancements of the range consensus algorithm (RANCO)[C]∥ION GNSS 2008,Savannah:ION,2008:93-103.

[4] Ene A,Blanch J,Powell J D.Fault detection and elimination for Galileo-GPS vertical guidance[C]∥NTM 2007,San Diego:ION,2007,1244-1254.

[5] Jiang Z,Groves P D,Ochieng W Y.Multi-constellation GNSS multipath mitigation using consistency checking [C]∥ION GNSS 2011,Portland:ION,2011:3889-3902.

[6] Schroth G,Ene A,Blanch J,et al.Failure detection and exclusion via range consensus[C]∥Proceedings of the European Navigation Conference,Toulouse:ECF,2008.

[7] Macabiau C,Gerfault B,Nikiforov I,et al.RAIM performance in presence of multiple range failures[C]∥NTM 2005,San Diego:ION,2005:779-791.

[8] Lee Y C,Braff R,Fernow J P,et al.GPS and Galileo with RAIM or WAAS for vertically guided approaches[C]∥ION GNSS 2005,Long Beach:ION,2005:1801-1825.

[9] Zhang M,Zhang J,Zhu Y.Enhancements of the dichotomy based RAIM[C]∥ION GNSS 2009,Savannah:ION,2009:2783-2790.

[10] Jiang Z,Groves P D.GNSS NLOS and multipath error mitigation using advanced multi-constellation consistency checking with height aiding[C]∥ION GNSS 2012,Nashville:ION,2012:79-87.