關于平衡態熱力學常見過程的定義

郭余年 程鐵欣

(1長春工業大學 吉林長春130012;2吉林大學化學學院 吉林長春130021)

平衡態熱力學所研究的是處于平衡態的封閉系統及其由一個平衡態變為另一個平衡態的過程。平衡態熱力學中的常見過程指的是等溫過程、等壓過程和等容過程。

1 等溫過程定義

1.1 等溫過程定義的說法

關于等溫過程的定義，存在著不同的說法。主要有以下3種:

說法1 系統的始態溫度T1等于終態溫度T2等于環境的恒定溫度T環(恒定)的過程為等溫過程［1-5］，即:

式中的“定值”不宜寫為“常數”，因為T不是量綱指數為0的純數。

說法2 系統與環境的溫度相等并恒定不變的過程為等溫過程［6-10］，定義式為:

式(2)中的T是所謂“過程中系統的溫度”。

說法3 其他說法。該說法是通過種種努力將說法1與說法2“統一”起來的說法，統稱為其他說法。由于說法1與說法2有差別，所以這些努力為等溫過程定義這個概念平添了一些混亂。

比較式(1)與式(2)知，這兩種說法都認為等溫過程是環境溫度恒定的過程，這是它們的共同點。由于過程中系統的溫度T恒定，自然滿足T1=T2，故說法1包括了說法2。但是，滿足T1=T2可能有兩種情況:一是過程中系統的溫度不恒定;一是恒定。即說法2是說法1的兩種可能情況之一，這是它們的差別。由于這個差別，它們描述的過程不完全相同。

1.2 等溫過程一例

等溫過程常見的實例是將具有透熱壁的系統放在與它始態溫度相同的一個熱源中進行的過程。

設有一活塞筒是透熱壁，活塞無質量且與筒壁無摩擦，筒內充有物質的量為n，壓力為p1，體積為V1，溫度為T的理想氣體。把它放在溫度為T的熱源(T環=定值)中。使氣體變為壓力為體積為V2，溫度為T的終態。氣體的該過程示意如下:

若以下面3種途徑完成這一過程:

(a)氣體恒外壓一次膨脹;

(b)氣體分3步恒外壓膨脹(三次膨脹);

(c)氣體在與環境的壓差為無限小的情況下連續地膨脹(準靜態膨脹)。

這3種途徑組成的過程都是等溫過程，它們的共性是都滿足式(1)。即說法1與此例相符;途徑(a)和途徑(b)是等溫不可逆過程，在不可逆過程中，系統必經歷非平衡態，因而，系統在不可逆過程中不可能存在均勻的溫度。例如，活塞筒內的氣體膨脹時，氣體各部分的密度、溫度和壓力并不完全相同，靠近活塞表面的氣體的密度要小些，溫度和壓力要低些;說法2與此不符，說法1對此并不排斥。途徑(c)是等溫可逆過程，在過程進行中，系統時刻處于(或無限接近于)平衡態，因而有一個與環境恒定溫度相等的溫度T，即T=T環=定值，此式即是式(2);亦即，說法2與此相符，說法1對此也可包容。所以，說法1作為等溫過程的定義是可取的;說法2定義的過程是等溫可逆過程，把它作為包括不可逆和可逆兩種情況的等溫過程的定義是不全面的。

對于此例(或類似此例)中的熱源的作用，也存在著不同的提法:提法①“以保持系統為恒溫”［11-13］;提法②“以使平衡時系統的溫度與熱源的溫度相等”［9］;提法③“以維持氣體的溫度”［1］。

作為系統的環境的熱源，是以地球、大氣、海洋等實際物體為背景抽象出來的理想化的客體，它應是物質的量與熱容為無限大的客體，它不因有限熱量的得失而變溫。因而為過程的進行提供一個恒溫環境(T環=定值)。在平衡態熱力學中，系統(或環境)過程的始態和終態都是平衡態［2］。在不存在絕熱壁的情況下，熱源的作用之一就是約束系統的始態及終態溫度與環境的恒定溫度相等。根據熱力學第零定律，溫度是描述系統平衡態的一個物理量;對于非平衡態系統，不能用溫度來描述它的狀態。所以，關于等溫過程中熱源的作用，提法①是不符合實際、不正確的，但它卻支持了等溫過程定義的說法2的觀點;提法②和提法③都是正確的。顯然，提法③比提法②簡練，但它易被誤解。

1.3 說法2定義的過程是等溫可逆過程

溫度是熱力學第零定律揭示出來的均相系統的一個平衡性質，并表述為溫度定理:“任一熱力學均相系統，在平衡態各自都存在一個狀態函數，稱之為溫度(T);它具有這樣的特性，對于一切互呈熱平衡的均相系統，其溫度彼此相等。”［14］將說法2與該定理對照有:① 在說法2定義的過程進行中，系統應時刻處于平衡態。根據過程進行中系統是處于平衡態還是非平衡態，將過程分為準靜態過程和非準靜態過程兩大類。非準靜態過程就是不可逆過程。因此，說法2定義的過程肯定不是(或不包括)不可逆過程，而只可能是準靜態過程;②在說法2定義的過程進行中，系統與環境應時刻處于熱平衡狀態。對于有傳熱的過程，系統與環境處于熱平衡狀態下的熱傳導，叫做“等溫熱傳導”。無摩擦的、系統與環境進行等溫熱傳導的準靜態過程(如上例中的途徑(c))是可逆過程。

在任一封閉系統的一個微變過程的Clausius不等式

中:＞適用于不可逆過程，=適用于可逆過程(下同);δQ是實際過程中系統與環境交換的熱量;T環(恒定)是環境的溫度，因為環境是熱源，在過程中其溫度恒定，記作T環(恒定);dS是過程中系統的熵變，其定義為:

式(4)中，δQr是過程可逆時系統與環境交換的熱量;T是系統的溫度。

假設該微變過程是可逆過程，式(3)中的δQ變為δQr且式(3)只取等號。有:

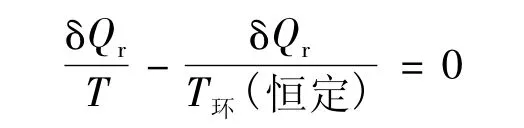
對于有傳熱的過程，δQr≠0，則由式(5)有:

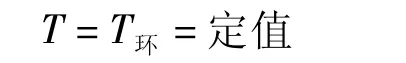
此式即是式(2)。從普適的式(3)至式(2)只附加了一個“可逆過程”的條件，即只有當過程是可逆時，過程中系統的溫度才等于環境的恒定溫度。亦即，說法2定義的過程是環境溫度恒定條件下的可逆過程。所以，說法2定義的過程是說法1定義的過程的可逆情況。如果把說法1定義的過程叫做等溫過程，則說法2定義的過程就是等溫可逆過程(或恒溫過程)。

1.4 定義的應用與檢驗

等溫過程定義的應用之一是在由判斷過程方向、限度的熵判據引出Helmholtz函數判據的演繹中，應用說法1進行該演繹可有多種方法:

方法＜1＞ 對于任一均相系統的任一有限過程，式(3)變為:(5)

若過程中環境對系統做的總功為 W;系統的熱力學能(U)的增量為 ΔU，由熱力學第一定律(ΔU=Q+W)，有:

式中ΔU≡U2-U1，ΔS≡S2-S1，若過程為說法1定義的等溫過程，則由式(1)，有:

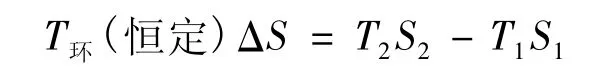
代入式(7)，有:

將均相平衡態系統的狀態函數(U-TS)稱為Helmholtz函數(A)，即:

式(9)適用于均相平衡態系統。將式(9)代入式(8)，有:

外推得:

式(10)和式(11)即為Helmholtz函數判據;下標T表示此2式適用于說法1定義的等溫過程，因為在由式(6)至此2式的演繹中應用了式(1)。

應用說法1進行熵判據至式(10)的過渡簡便且直觀，物理意義清楚，結果正確。那么可否應用說法1從熵判據直接得到式(11)呢?有人認為不可能，因為說法1是針對有限過程定義的;只有說法2才能解決這個問題，因為它是對無限小過程進行定義的。其實不然。

方法＜2＞ 對均相系統的任一微變過程，式(7)變為:

對于等溫過程，由式(1)，有:

即:

即:

將式(9)代入式(15)，得式(11);外推得式(10)。

方法＜3＞ 由于在等溫過程定義的說法1中，系統的始態、終態以及環境(熱源)的溫度是任意指定的。若該溫度指定為T(如上例)，則由式(1)，有:

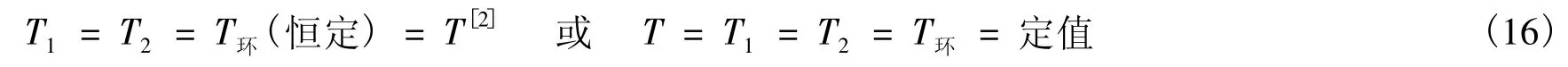
在式(16)中，T是系統任一平衡態的溫度。由式(16)，有:

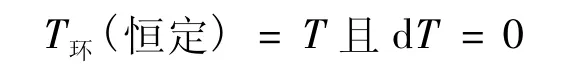
則:

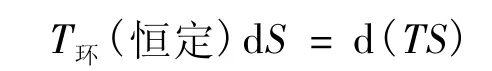
代入式(12)得式(15)，經式(9)得式(11);外推得式(10)。

2 等壓過程定義

對于等壓過程的定義，也有與等溫過程定義類似的各種說法:

說法1 系統始態壓力p1等于終態壓力p2等于環境的恒定壓力p環(恒定)，即:

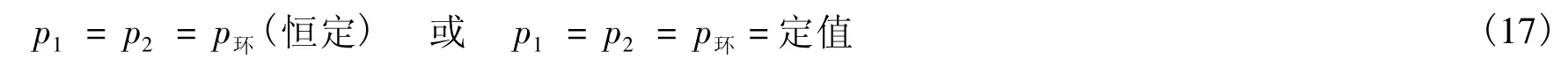
的過程為等壓過程［2-5］。

說法2 系統與環境的壓力相等并恒定不變的過程為等壓過程［6-9］，其表達式為:

式(18)中的p是所謂“過程中系統的壓力”。

說法3 其他說法。該說法是通過各種努力將說法1與說法2“統一”起來的說法，統稱為其他說法。由于說法1與說法2有差別，所以這些努力為等壓過程定義這個概念帶來了一些混亂。

壓力(p)只在系統的平衡態中才有明確的意義，系統在非平衡態時不存在均勻統一的壓力。因此，說法2定義的過程是說法1定義的過程的準靜態過程。如果把說法1定義的過程叫做等壓過程，則說法2定義的過程是等壓準靜態過程或進一步理想化的等壓可逆過程(或恒壓過程)。所以，將說法2作為等壓過程的定義是不合適的。

等壓過程定義的應用之一是在引出Gibbs函數判據的演繹中，并在演繹中接受檢驗。應用說法1進行該演繹可有以下方法:

方法＜1＞ 將過程的總功W分為體積功W體和非體積功W'。由體積功的定義(δW體=－p環dV)知，對于式(17)定義的等壓過程，有:

對等溫等壓過程，由式(10)與式(19)，有:

定義平衡態均相系統的狀態函數(A+pV)為系統的Gibbs函數(G)，即:

式(21)適用于平衡態均相系統。將式(21)代入式(20)，有:

或:

在式(22)與式(23)中，下標T，p表示此2式適用于式(1)和式(17)定義的等溫等壓過程，此2式即是Gibbs函數判據。

方法＜2＞ 對均相系統等溫等壓微變過程，式(11)可改寫為:

由式(17)，有:

即:

即:

將式(21)代入式(27)得式(23);外推得式(22)。

方法＜3＞ 等壓過程常見的實例是在不存在剛壁的情況下，將系統放在與它始態壓力相同的一個恒壓環境(p環=定值)中進行的過程。若指定任一平衡態均相系統的壓力為p的狀態為始態，即p=p1，則對由式(17)定義的等壓過程，有:

形似式(18)的式(28)中的p為任一平衡態均相系統的壓力。由式(28)，有:

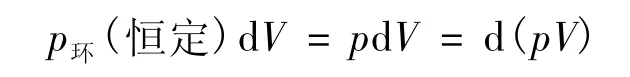
代入式(24)，經式 (21)得式(23);外推得式(22)。

3 等容過程定義

對等容過程的定義，也存在著不同的說法。主要有:

說法1 系統體積V恒定不變，即:

的過程為等容過程。

說法2 系統的始態與終態體積相等，即:

的過程為等容過程。

說法3 說法3是將說法1與說法2放在一起的說法。例如有的給出了定義式“V=V1=V2=定值”。

雖然對定義有不同的說法，但在應用中各種說法的作者都采用的是說法1，即等容過程就是系統的體積恒定不變的過程。等容過程一般是指在剛性密閉容器中或凝聚系統發生的過程。

4 小結

系統與環境的溫度(或壓力)相等并恒定的過程，是等溫(或等壓)過程極限情況的可逆過程，關于可逆過程的實質，有一句名言:“在尋常的實驗時間里，可逆過程等于沒有過程，也就是平衡狀態。”［16］

［1］傅鷹.化學熱力學導論.北京:科學出版社，1963

［2］吉林工業大學，吉林工學院.物理化學.北京:機械工業出版社，1980

［3］王明德.大學化學，2011，26(4):72

［4］朱文濤.基礎物理化學(上冊).北京:清華大學出版社，2011

［5］楊永華.物理化學.北京:高等教育出版社，2012

［6］胡英.物理化學(上冊).北京:人民教育出版社，1979

［7］胡英.物理化學(上冊).第3版.北京:高等教育出版社，1988

［8］胡英.物理化學(上冊).第5版.北京:高等教育出版社，2007

［9］天津大學物理化學教研室.物理化學(上冊).第4版.北京:高等教育出版社，2001

［10］朱志昂，阮文娟.近代物理化學(上冊).第4版.北京:科學出版社，2008

［11］傅獻彩，沈文霞，姚天揚，等.物理化學(上冊).第5版.北京:高等教育出版社，2005

［12］傅獻彩，陳瑞華.物理化學(上冊).第3版.北京:高等教育出版社，1979

［13］傅獻彩，沈文霞，姚天揚.物理化學(上冊).第4版.北京:高等教育出版社，1990

［14］韓德剛，高執棣，高盤良.物理化學.第2版.北京:高等教育出版社，2009

［15］沈文霞.物理化學核心教程.第2版.北京:科學出版社，2009

［16］黃子卿.物理化學.北京:高等教育出版社，1955