基于EEMD分解的輸電塔阻尼特性識別

沈國輝， 項國通， 邢月龍， 郭 勇， 孫炳楠

(1.浙江大學 土木工程學系，杭州 310058;2.華南理工大學 建筑設計研究院，廣州 510640;3.浙江省電力設計院，杭州 310007)

風荷載是輸電塔的主要控制荷載，準確合理地計算輸電塔在風荷載作用下的動力響應具有重要意義。輸電塔的風振響應具有隨機、非平穩和非線性等特征，其阻尼特性的識別一直是個難題。通常根據結構動力響應的時間歷程來評估阻尼，阻尼的識別方法可以分成兩大類，即譜方法和時間序列法。用于阻尼識別的輸電塔響應時程通常來源于現場實測和氣彈模型風洞試驗。

汪江等［1－3］實測了某輸電塔的加速度響應，利用半功率譜帶寬法識別結構的各階模態阻尼。但有研究表明［4］，半功率譜帶寬法由于受到信號處理中的采樣頻率、頻率分辨率、采樣長度等因素影響，識別的阻尼比數據離散較大且不穩定。李正良等［5－8］基于輸電塔氣彈模型風洞試驗的加速度測試結果，利用經驗模態分解法(Empirical Mode Decomposition，EMD)獲得本征模態函數(Intrinsic Mode Function，IMF)，結合隨機減量法和Hilbert變換識別輸電塔氣彈模型的整體阻尼和氣動阻尼。EMD方法在處理非線性、非平穩時間序列表現出一定的優勢，但采用EMD方法時可能會存在一定程度的模態混疊現象［9－10］。鑒于EMD方法的不足，Wu等［11］在EMD方法基礎上添加了噪聲輔助分析，提出了集合經驗模態分解法(Ensemble Empirical Mode Decomposition，EEMD)。目前利用EEMD方法進行結構物(包括輸電塔)阻尼特性識別的研究幾乎沒有。

本文以一典型的輸電塔為例，分6個風速和7個風向角在B類地貌下進行氣彈模型測振風洞試驗，分別采用EMD和EEMD方法分解風洞試驗獲得的加速度時程，對比兩種分解方法得到的IMF以分析EEMD方法的優越性，然后運用EEMD方法、改進的隨機減量法和Hilbert變換法識別輸電塔氣彈模型在各風速和風向角下的頻率和阻尼，并探討輸電塔順線向和橫線向阻尼隨風速和風向的變化特征，為結構物的阻尼識別方法和輸電塔的振動特性研究提供參考。

1 阻尼的識別原理和方法

1.1 經驗模態分解法(EMD)

經驗模態分解法基于信號局部特征的時間尺度，從信號中提取出本征振動模態，采用本征模態函數(IMF)來反應原信號。IMF須滿足如下兩個條件:①在信號的整個持續時間內，零交點的數目與極值點的數目必須相等或至多相差一個;②在任意時刻，由局部極大值點定義的上包絡線和由局部極小值點定義的下包絡線之間的平均值為零。

Huang等［9］發展了一種將任意信號分解成本征模態函數(IMF)分量的方法，即經驗模態分解法。與其他信號處理方法相比，EMD方法是直接的、后驗的、自適應的，其分解基是源自于原始信號。該方法的實質是通過特征時間尺度來識別信號中所固有的本征振動模態。EMD分解的核心是篩分過程，通過篩分得到IMF。篩分的處理過程為:將信號波形中所有局部極大值點和局部極小值點識別出來，用三次樣條曲線將所有局部極大點(極小值)連接起來構成原始波形的上(下)包絡線，求出上下包絡的平均值，將原始信號減去平均值即為一次篩分過程。

EMD存在模態混疊問題，其原因為信號的間斷。間斷使得時域空間的某些尺度丟失，不僅引起了嚴重的模態混疊，而且使單獨的IMF分量缺乏物理意義。為了減輕EMD方法的模態混疊，Huang等［12］曾提出了間斷測試，但模態混疊問題并沒有得到非常好的解決。另外，EMD方法邊界問題的處理也是一大難點，目前工程上常用的EMD邊界處理方法有鏡像法、神經網絡預測、多項式外延方法等，但各自都有其局限性。

1.2 集合經驗模態分解法(EEMD)

集合經驗模態分解(EEMD)［11］把一個全體測試的均值定義為真實的本征模態函數分量，其中每個測試都包含了信號和有限幅值的白噪聲，使用該方法能夠明確地分離出各個尺度的信號，不用任何預先的主觀標準選擇。

EEMD的原理為:當信號加入均勻分布的白噪聲背景時，不同尺度的信號區域將自動映射到與背景白噪聲建立的相關的、適當的尺度上;每次獨立的試驗可能會產生信噪比很大的結果，但足夠多的試驗全體均值將會消除噪聲;全體的均值將會被認為是真正的結果，當試驗的個數足夠多時，試驗全體均值中唯一存在的部分是信號本身。

EEMD方法的實現過程如下［11］:

(1)在目標數據上加入白噪聲序列;

(2)將加入白噪聲后的序列分解為IMF;

(3)每次加入不同的白噪聲序列，重復步驟1、步驟2;

(4)把每次分解得到的相應IMF的均值作為最終的結果。

1.3 改進的隨機減量法(RDT)

隨機減量法(Random Decrement Technique，RDT)利用隨機信號的平均值接近于零的特點，通過時間平均從隨機振動信號中提取自由衰減響應。該方法將線性系統在任意激勵下的響應看成三個部分組成，即由初位移引起的自由振動、初速度引起的自由振動和隨機激勵引起的強迫振動。通過大量合理選擇的時間片段累加后，獲得只有初始位移的自由振動信號。

為了解決信號提取中截取閥值和平均次數的矛盾，本文利用改進的隨機減量法［13］，采用了正、負閥值同時截取的提取方法。對于隨機響應信號，由正閥值和負閥值截取的信號段具有相同的物理意義。顯然，對負閥值截取子信號段變號后再參與疊加平均，就可使參與平均的項增多，使提取的隨機特征信號的質量得到提高。

1.4 Hilbert變換和阻尼識別

利用EMD或EEMD方法獲得IMF分量后，利用RDT方法提取自由振動衰減信號 X(t)，對其進行Hilbert變換為Y(t):

其中P為廣義積分的Cauchy主值，由X(t)和Y(t)可以構成一個解析信號:

由Hilbert變換得瞬時幅值a(t)、瞬時相位 θ(t)如下:

對于小阻尼的單自由度系統，對幅值和相位分別引入對數和微分算子，可得:

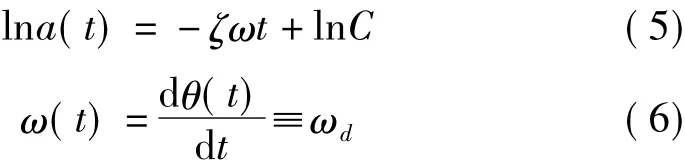
式中為阻尼比，C為常數，ω為瞬時頻率，ωd為有阻尼系統的頻率。設ln a(t)的斜率為p1，θ(t)的斜率為p2(即為頻率ωd)，則可識別得阻尼比ζ為:

2 某輸電塔的氣彈模型風洞試驗

某輸電塔高74.5 m，塔身的平面形狀為正方形，其氣彈模型采用離散等代剛度法［14］制作，主要考慮輸電塔的拉伸剛度相似。模型按1:45縮尺比制作，全塔共有806個桿件，全部采用薄壁銅管和不銹鋼無縫毛細管焊接制作，模型通過鋼板固定于剛性底座。為了保證受風面積的相似要求，模型桿件外徑不足部分首先采用無剛度的泡沫紙外包再用膠帶紙封裹，做到幾何相似。模型桿件直徑為0.4～9.9 mm，桿件壁厚為0.1～0.2 mm，經動力特性標定試驗后得到模型相似系數如表1所示，模型的風洞試驗照片如圖1所示。由于模型為格構式鏤空結構，風洞阻塞度不需要修正。

表1 氣彈模型的相似系數Tab.1 Similarity coefficients of aero－elastic model

圖1 輸電塔模型的風洞試驗照片Fig.1 Pictures of latticed tower model in wind tunnel

該輸電塔的風洞試驗在浙江大學ZD－1風洞中進行，試驗段長18 m、高3 m、寬4 m。三角尖劈和地面粗糙元置于來流前部，如圖1所示，用來模擬B類地貌的大氣邊界層。根據建筑結構荷載規范［15］要求，B類地貌大氣邊界層的平均風速V剖面按指數規律變化。對于湍流度Iu剖面，參考日本AIJ規范［16］有:

式中z為高度，α為地面粗糙度指數，對于B類地貌取0.16。需要說明的是，試驗時由于荷載規范2012版尚未頒布，因此仍采用2001版荷載規范的規定。風洞模擬的風速和湍流度剖面如圖2所示，圖中平均風速剖面以塔頂高度h的風速為基準進行無量綱處理。由圖2可知風洞中很好地模擬了B類地貌的邊界層。

在模型上布置12個加速度傳感器(每只質量約為2 g)，沿X向(順線向)、Y向(橫線向)各布置6只，靈敏度系數為 0.061 6～0.144 mV/EU，信號采集采用TST5912動態信號測試系統。測試的風向角β及坐標X、Y的方向定義如圖3所示。

圖2 風洞模擬的平均風速和湍流度剖面Fig.2 Simulated profiles of mean velocity and turbulence intensity in wind tunnel

圖3 風向角及坐標系統的定義Fig.3 Definition of wind direction and coordinate system

3 EMD與EEMD分解結果的比較

在測試風速18 m/s時0°風向角下輸電塔頂部順線向的加速度時程如圖4所示，取1.4 s到1.8 s之間的數據片段進行研究。分別采用EMD和EEMD方法提取各階IMF模態，為了抑制EMD和EEMD分解的端部效應，采用Rilling等［17］建議的鏡像法進行端部數據的處理。

圖5給出了EMD和EEMD方法針對圖4時程進行IMF分解的結果，計算中EEMD方法所加白噪聲幅值取為待分解加速度時程均方根的0.2倍，樣本數取500。由圖6可知，EEMD方法明顯比EMD方法具有更好的分解效果，基于EEMD方法的結果較理想，各階振蕩模態清晰。基于EMD方法的結果存在著一定的模態混疊情況，如圖中時間軸1.6 s到1.7 s段，IMF1的結果(圖5(a))混疊了IMF2的部分振蕩模態(圖5(b))，IMF3的結果(圖5(c))混疊了IMF4的部分振蕩模態(圖5(d))。同時基于 EMD方法的結果在IMF4中還存在騎行波(時間軸1.6 s到1.7 s段)，分解結果并不理想。因而EEMD方法分解得到IMF結果更加理想，后面的模態和阻尼識別均基于EEMD方法。

圖4 某測點的加速度時程Fig.4 Time history of acceleration on a measured point

4 輸電塔阻尼的識別過程

以輸電塔頂部橫線向的加速度為例，對其在0°風向角、12 m/s試驗風速下的加速度時程進行EEMD分解，數據采樣頻率為500 Hz，采樣時間為20 s。對EEMD分解得到的前四階IMF采用改進的隨機減量法提取相應的自由衰減時程c1(t)、c2(t)、c3(t)和c4(t)，如圖6所示，隨機減量法中的子樣本時間長度為0.4 s。

由圖6可知，c1至c4均呈現振幅的自由衰減情況，其中c2和c3最為明顯，且曲線均比較光滑。將圖6的時程進行Hilbert譜變換，獲得瞬時頻率隨時間的變化曲線，其中c3的瞬時頻率如圖7所示。可知c3對應的頻率為28 Hz左右，與輸電塔模型橫線向的一階頻率剛好吻合，因此EEMD分解后的IMF3代表了輸電塔模型橫線向的一階振動。c3時程的自然對數lnα(t)和瞬時相位θ(t)隨時間的變化曲線如圖8所示，采用擬合方法獲得其斜率，再根據式(7)計算得其阻尼比為0.031。

圖5 EMD和EEMD分解模態的比較Fig.5 Comparison of decomposition modes obtained from EMD and EEMD methods

5 輸電塔總阻尼的識別結果

在風洞中對輸電塔模型進行6個風速(8 m/s、10 m/s、12 m/s、14 m/s、16 m/s、18 m/s) 和 7 個風向角(0°、15°、30°、45°、60°、75°、90°)下的測振試驗。根據頂部的加速度測試結果，采用EEMD分解法結合改進的RDT法和Hilbert變換，識別主IMF對應的自振頻率和總阻尼比，其中順線向的數據如圖9所示，橫線向的數據如圖10所示。需要說明的是，圖中的阻尼為風荷載作用于輸電塔上的總阻尼比，包含了結構阻尼和氣動阻尼。結構阻尼通常可以采用敲擊法進行識別，在實際操作中發現測試獲得的結構阻尼比較離散，其原因主要為阻尼與振動幅度有很大的關系，通常認為結構阻尼隨著振動幅度的增大而增大［18］。因此本文不分離出結構阻尼和氣動阻尼，采用總阻尼來表示。

由圖9可知，輸電塔順線向的自振頻率總體上隨著風速的增大而呈減小趨勢，在文獻［6］中也發現該規律，頻率減少的一個原因是與高風速下總阻尼增大有關;順線向的總阻尼隨著風速的增大總體上呈單調增大趨勢。由圖10可知，輸電塔橫線向的自振頻率總體上隨著風速的增大而呈減小趨勢，但離散度比圖9中的順線向數據大;而橫線向總阻尼的規律性不明顯，在風洞風速10 m/s時有一個突增，然后隨著風速增大呈略有增加的趨勢。

圖6 各階IMF采用隨機減量法處理后的時程Fig.6 Time histories of IMF modes after treatment of RDT

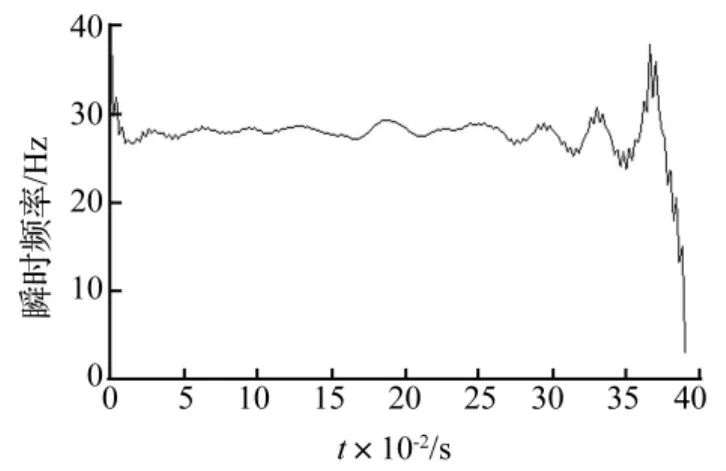
圖7 c3的瞬時頻率Fig.7 Instantaneous frequencies of c3

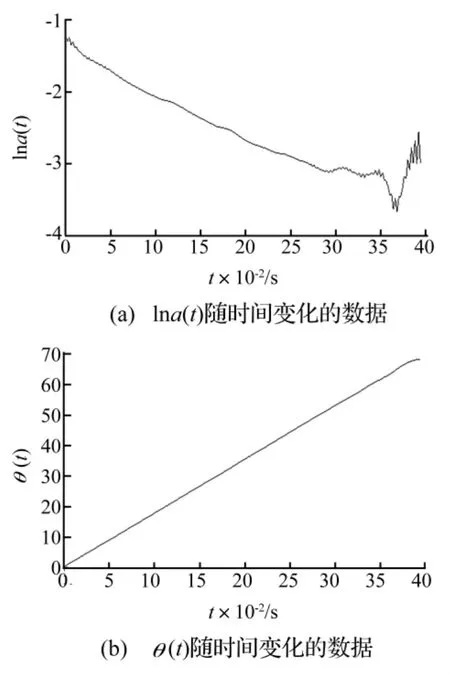
圖8 ln a(t)和θ(t)隨時間的變化曲線Fig.8 Curves of ln a(t)and θ(t)with respect to time

圖9 順線向頻率和阻尼的識別Fig.9 Identification of frequency and damping in along-line direction

圖10 橫線向頻率和阻尼的識別Fig.10 Identification of frequency and damping in cross-line direction

針對圖9和圖10所反映的輸電塔順線向和橫線向的振動特性，作討論如下。輸電塔的風致振動主要由風繞輸電塔桿件引起，風穿過輸電塔桿件會產生復雜的空氣動力學現象，包含了漩渦脫落、渦激振動、尾流干擾等。相比而言，順線方向的氣動現象(風穿過兩片桁架)比橫線方向的氣動現象(風在橫擔處需要穿越很多層桁架，具體見圖1)相對簡單一些，因而輸電塔的頻率和阻尼隨風速風向變化的規律性在順線方向(見圖9)比在橫線方向(見圖10)要好很多很多。文獻［19］從風力譜角度也提到:順風向(對于0°風向即為順線向)脈動風力譜是一種典型的縱向風湍流譜，而橫風向(對于0°風向即為順線向)力譜較為復雜，這從另一個方面支持了本文的觀點。

6 結論

本文研究基于EEMD的阻尼特性識別方法和輸電塔阻尼分布特性，有以下結論:

(1)本文實例發現從加速度時程中分解IMF時采用EEMD方法比EMD方法具有更好的分解效果，基于EEMD方法的IMF時程振蕩模態更清晰，而基于EMD方法的結果存在著一定程度的模態混疊，因此推薦使用EEMD方法。

(2)采用EEMD分解法結合改進的RDT法和Hilbert變換，可以從結構響應時程中識別出主IMF對應的頻率和阻尼，在動力特性識別時推薦使用。

(3)輸電塔順線向的自振頻率總體上隨著風速的增大而呈減小趨勢，順線向的總阻尼隨著風速的增大而增大，而橫線向頻率和阻尼隨風速變化的規律性不明顯。

(4)風穿過輸電塔桿件會產生復雜的空氣動力學現象，包含了漩渦脫落、渦激振動、尾流干擾等。相比于順線方向，輸電塔在橫線方向時風需要繞過更多層桁架，反應在動力特性上便是順線方向的動力特性隨風速變化的規律性更好。

［1］汪江，杜曉峰，田萬軍，等.500 kV淮蚌線淮河大跨越輸電塔振動測試與模態識別［J］.中國電力，2009，42(2):30－33.WANG Jiang， DU Xiao-feng， TIAN Wan-jun， et al.Dynamic testing and model identification of long-span power transmission tower located in 500 kV Huaibeng Line［J］.Electric Power，2009，42(2):30 －33.

［2］何敏娟，閆祥梅，張益國，等.兩相鄰輸電塔的同步環境脈動實測試驗研究［J］.振動與沖擊，2009，28(11):155－158.HE Min-juan， YAN Xiang-mei， ZHANG Yi-guo， et al.Synchronous test study of two adjacent transmission tower undergoing ambient excitations［J］.Journal of Vibration and Shock，2009，28(11):155 －158.

［3］胡宇濱，馬人樂.江陰500 kV輸電塔動力性能測試［J］.結構工程師，2002，3:62－66.HU Yu-bin，MA Ren-le.Site experiment of dynamic behavior for Jiangyin 500 kV transmission tower［J］.Structural Engineers，2002，3:62 －66.

［4］應懷樵，劉進明，沈松.半功率帶寬法與 INV阻尼計法求阻尼比的研究［J］.噪聲與振動控制，2006，2:4－6.YING Huai-qiao，LIU Jin-min，SHEN Song.Half-power bandwidth method and INV damping ration solver study［J］.Noise and Vibration Control，2006，2:4 －6.

［5］李正良，肖正直，韓楓，等.1 000 kV漢江大跨越特高壓輸電塔線體系氣動彈性模型的設計與風洞試驗［J］.電網技術，2008，32(12):1－5.LI Zheng-liang， XIAO Zheng-zhi， HAN Feng， et al.Aeroelastic model design and wind tunnel tests of 1 000 kV Hanjiang long span transmission line system［J］.Power System Technology，2008，32(12):1 －5.

［6］任坤，李正良，肖正直，等.環境激勵下特高壓輸電塔線體系氣動阻尼的識別［J］.重慶工學院學報(自然科學版)，2009，23(7):64 －68.REN Kun， LI Zheng-liang， XIAO Zheng-zhi， et al.Aerodynamic damping identification of UHV transmission line system under ambient excitation［J］.Journal of Chongqing Institute of Technology(Natural Science)，2009，23(7):64－68.

［7］郭勇.大跨越輸電塔線體系的風振響應及振動控制研究［D］.杭州，浙江大學，2006.

［8］熊鐵華，梁樞果，鄒良浩.基于完全氣彈模型風洞試驗輸電塔風荷載識別［J］.建筑結構學報，2010，31(10):48－54.XIONG Tie-hua，LIANG Shu-guo，ZOU Liang-hao.Wind loading identification of transmission towers based-on wind tunnel tests of full aero-elastic model［J］.Journal of Building Structures，2010，31(10):48 －54.

［9］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London(series A)，1998，454(1971):903－995.

［10］項國通.格構式圓截面鋼管塔風荷載特性的風洞試驗研究［D］.杭州，浙江大學，2013.

［11］ Wu Z H， Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method［J］.Advances in Adaptive Data Analysis.2009，1(1):1 －41.

［12］ Huang N E，Shen Z，Long S R.A new view of nonlinear water waves:the Hilbert spectrum［J］.Annual Review of Fluid Mechanics.1999，31(1):417 －457.

［13］張西寧，屈梁生.一種改進的隨機減量信號提取方法［J］.西安交通大學學報，2000，34(1):106－107.ZHANG Xi-ning，QU Liang-sheng.Improved method for extracting of random decrement signal［J］.Journal of Xi’an Jiaotong University，2000，34(1):106 －107.

［14］郭勇，孫炳楠，葉尹，等.大跨越輸電塔線體系氣彈模型風洞試驗［J］.浙江大學學報(工學版)，2007，41(9):1482－1486.GUO Yong，SUN Bing-nan，YE Yin，et al.Wind tunnel test on aeroelastic model of long span transmission line system［J］.Journal of Zhejiang University(Engineering Science)，2007，41(9):1482 －1486.

［15］建筑結構荷載規范(GB50009－2001)［S］.北京:中國建筑工業出版社，2002.

［16］ Architectural Institute of Japan.Recommendations for loads on buildings［M］. Japan: Architectural Institute of Japan，2004.

［17］ Rilling G，Flandrin P，Goncalves P.On empirical mode decomposition and its algorithms［C］.IEEE Workshop on Nonlinear Signal and Image Processing NSIP－03，Grado(I)，2003.

［18］嵇學培，謝壯寧，李小康.廣州西塔風致響應和氣動阻尼特性的試驗研究［J］.土木工程學報，2009，42(7):58－64.JI Xue-pei， XIE Zhuang-ning， LI Xiao-kang. An experimental study on the wind induced response and aerodynamic damping of Guangzhou west tower［J］.China Civil Engineering Journal，2009，42(7):58 －64.

［19］張慶華，顧明，黃鵬.格構式塔架風力特性試驗研究［J］.振動與沖擊，2009，28(2):1－4.ZHANG Qing-hua，GU Ming，HUANG Peng.Experimental study of wind force on latticed tower［J］.Journal of Vibration and Shock，2009，28(2):1 －4.