子群的Fs擬正規性對Sylow塔群結構的影響

王 輝, 胡 濱

(江蘇師范大學 數學與統計學院,江蘇 徐州 221116)

0 引言

本文中,所有群均是有限群,未交待的概念和符號參見文獻[1]和[2].

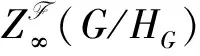
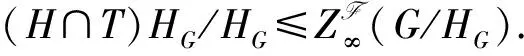
顯然,對于任一非空群系F，所有的正規子群、c正規子群、Fn可補充子群、Fh正規子群、置換子群、s置換子群都是Fs擬正規子群.但反之不成立(參見[11]中例1.2).

本文主要利用Fs擬正規子群,得到了關于Sylow塔群的一些新的判別準則.

1 有關概念和基本結果

設G是一個群,p1>p2>…>pt是G的不同的素因子,如果存在G的Slyowpi子群Pi(i=1,2,…,t),使得P1P2…Pk正規于G,則稱G具有Sylow塔性(或稱G是一個Sylow塔群).

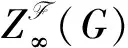
群類F稱為一個群系,如果F是同態像封閉且次直積封閉.群系F稱為飽和群系,如果當G/Φ(G)∈F時,總有G∈F.群系F稱為S閉的,如果G∈F時,G的每個子群都屬于F.眾所周知,所有Sylow塔群構成的群類和所有超可解群構成的群類U都是S閉的飽和群系.

引理1[11]設F是一個群類,H≤K≤G.下列結論成立:

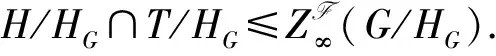
4) 如果H在G中Fs擬正規,且F是S閉的,那么H在K中Fs擬正規.

5) 若G∈F,則G的每個子群在G中Fs擬正規.

引理2[13]假設F是包含所有超可解群的飽和群系,群G有一個正規子群E,使得G/E∈F.若E循環,則G∈F.

引理3[14]設G是一個有限群,如果G的子群H在G中s置換,則H/HG是冪零的.

引理4[15]設G是一個群,A≤G.若A次正規于G,且A是可解群,則A包含在G的某個可解正規子群中.

引理5[16]若H在G中s置換,且H是一個p群,對某一素數p,則Op(G)≤NG(H).

2 主要結論

定理1設F是一個具有Sylow塔性的群類.若群G的每個非循環Sylow子群的極大子群在G中Fs擬正規,則G∈F.

證根據[11,定理3.1],G是超可解群,從而G是Sylow塔群.

定理2設F是一個具有Sylow塔性的群類,則群G∈F當且僅當G=AB,其中A在G中s置換,B∈F,且A的每個非循環Sylow子群的極大子群……