利用線性規劃進行金工實習中心資源優化配置的探討

◆葉鐘輝

作者：葉鐘輝，南京工業大學實習教師（210009）。

1 引言

隨著高校的不斷擴招，高校學生人數不斷增加。緊隨而來的是各高校在師資、設備、儀器等軟、硬件方面投入也在不斷增長，如何能在有限的資源投入情況下，盡可能地合理分配好資源，使其盡可能地發揮其作用，成為現在急需解決的一個問題。

2 研究內容

學生參加金工實習是大學高等教育的一個重要組成部分，通過各個工種的實習，一個學生最終完成金工實習的學業。通常，不同的機床、設備所能承擔的實習學生數是不相同的。例如，一臺車床最多能承擔1名學生參加實習，而一臺銑床卻能承擔4名學生參加實習。另外，由于學生在實習過程中要分成多個小組，在不同的實習工種中同時進行，不同小組的學生雖然都要實習同樣的所有工種，但他們實習的順序不同，這就如同產品生產中工藝不同一樣。因此，不同小組的學生參加實習的實習流程是不一樣的。每一批學生實習，都是由不同的幾個實習流程組成。本文研究的，就是通過資源優化，使得有限的投入在金工實習中發揮最大作用，盡可能地多承擔一些學生參加金工實習。

3 模型的提出

為完成學生的實習任務，金工實習各實習工種內需配置各種資源，包括人力資源——實習教師，物力資源——機床設備、各種材料、機物料等。實習中心應如何配置這些資源，才能使金工實習中心以盡可能少的資源滿足每年實習學生的需要？原有的資源是否能夠滿足？需要添置多少資源？哪些資源？這些問題都要通過線性規劃來解決。

對于資源優化配置，目前有許多種方法，而線性規劃是應用最為廣泛的一種系統優化的方法。下面要建立線性規劃的數學模型[1-3]，首先做如下假設：

金工實習中心實習過程中共經歷i個工種，各個工種內每批學生所需要的實習教師成本為a1,a2,…,ai，各個工種所配備機床設備的成本為b1,b2,…,bi，材料、機物料消耗的成本為c1,c2,…,ci，各工種每批所能承擔的學生數為n1,n2,…,ni，各工種承擔學生的批次為x1,x2,…,xi，各個工種實習成本為Mi=ai+bi+ci，所承擔的實習學生總數為Zmax=x1n1+x2n2+…+xini。將Zmax作為目標函數，求其最大值。金工實習中心全年的實習學生總數為Q，Q≤Z成為約束條件之一，各工種每年學生成本的投入也是約束條件之一。考慮到x1,x2,…,xm的實際意義，要求x1,x2,…,x8為整數。

綜合以上的條件構成如下線性規劃：

目標函數：Zmax=x1n1+x2n2+…+xini

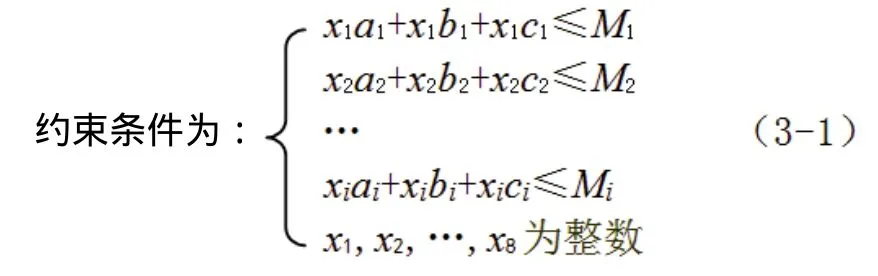
4 算法實例

南京工業大學金工實習中心資源數據 南京工業大學金工實習中心是南京工業大學內為學生提供實習培訓的部門。學生參加金工實習，需經歷車工、鉗工、鑄工、焊工、普銑磨、數控銑、數控車、線切割等八個工種的實習。

1）機床設備主要用于學生的金工實習，無法作為他用。因此，每年的設備折舊成為其消耗的成本之一。

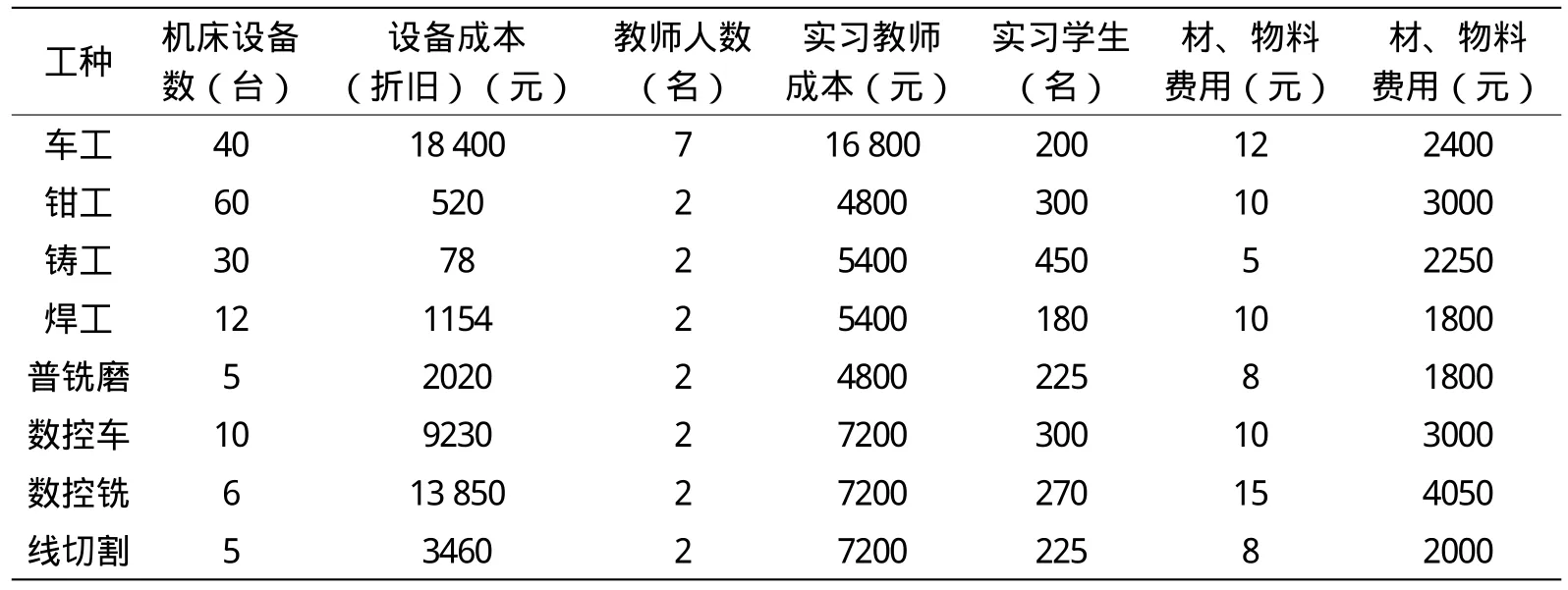
表1 金工實習現階段資源數據表（15天／批）

2）教師指導金工實習，要有工資收入，這也構成學生參加實習的成本消耗。金工實習中心現有金工實習教師21人，各工種教師工資成本也不盡相同。

3）材料、物料等資源消耗也有一定的成本。

這三部分就基本構成學生參加金工實習的主要資源消耗，如表1所示。

另外，在南京工業大學金工實習中心2012學年的金工實習中，機械類學生的實習時間為四周，非機類學生的實習時間為三周，而全年一共實習40周，因此，全年最多實習14批次學生。由于學生是分成四個大組循環實習，車工、鉗工各一個大組，三個數控工種組成一個大組，鑄、焊、銑磨為一大組；又由于這次學校投入資金主要用于機床設備的購買，而且先進的數控設備占據多數，而教育部最新規定，在現代數控設備投入上，比例不得低于25%，高可達到50%，每組分擔的學生數應基本相同，因此，應有如下約束條件：

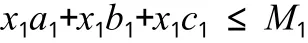
考慮到x1,x2,…,xm的實際意義，要求14≤

x1,x2,…,x8≤28，并且為整數。綜合以上條件構成如下線性規劃：

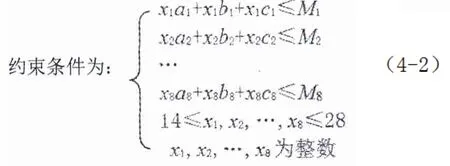
南京工業大學金工實習中心現有車床、銑床、數控銑、數控車、線切割機床等多種設備，總體價值約750萬元；現學校決定投入250萬元用于購置設備，則機床設備預計價值1000萬元，按10年折舊期計算，每年的設備成本約為100萬元；學校核定實習教師人數為25人，則工資成本每年約為120萬元；另外，學校每年核定35萬元機、物料成本費，如表2所示。

表2 金工實習資源限量表

金工實習中心所能容納實習學生人數最大的線性規劃模型為：

約束條件為：

對原問題模型，加入松弛變量轉化為標準形式。列出其初始單純形表如表3所示。

通過數次迭代計算，得出最優解如表4所示。

由于金工實習中心每學年有40周，每周5個工作日，因此，每學期，學生實習接待批次為40×5÷15≈14批，如表5所示。現有金工實習教師必須保證工作量的飽滿，14批 要安排的，至于超過14批的學生，需設備、引進新的金工實習教師，投入更多的實習用機、物料來完成。通過上述線性規劃的最優解求解，得出結果如表6所示。比較表5、表6，可得表7。

表3 初始單純形表

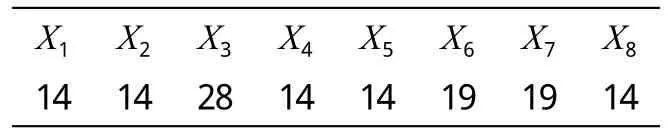
表4 金工實習資源配置最優解

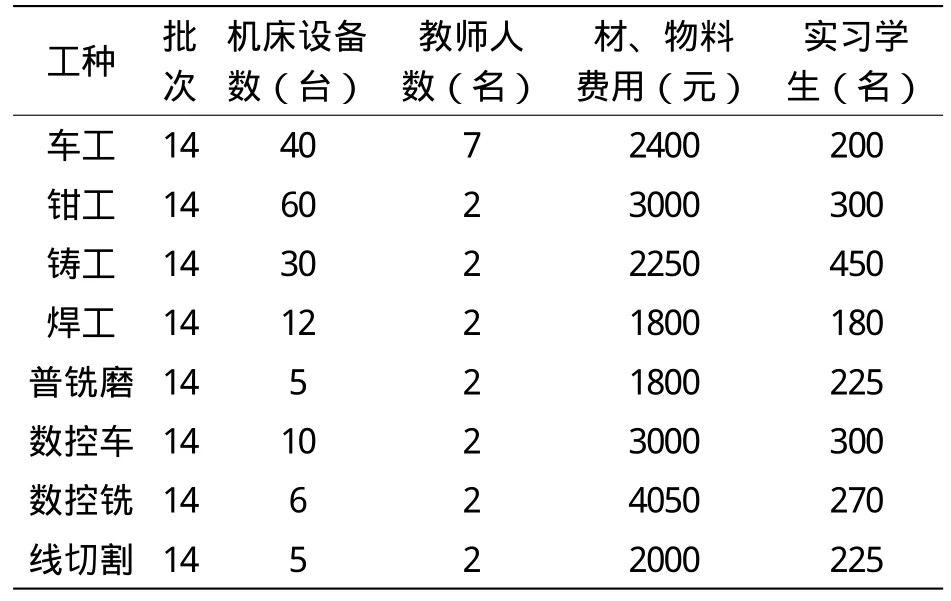
表5 金工實習資源配置表（規劃前）

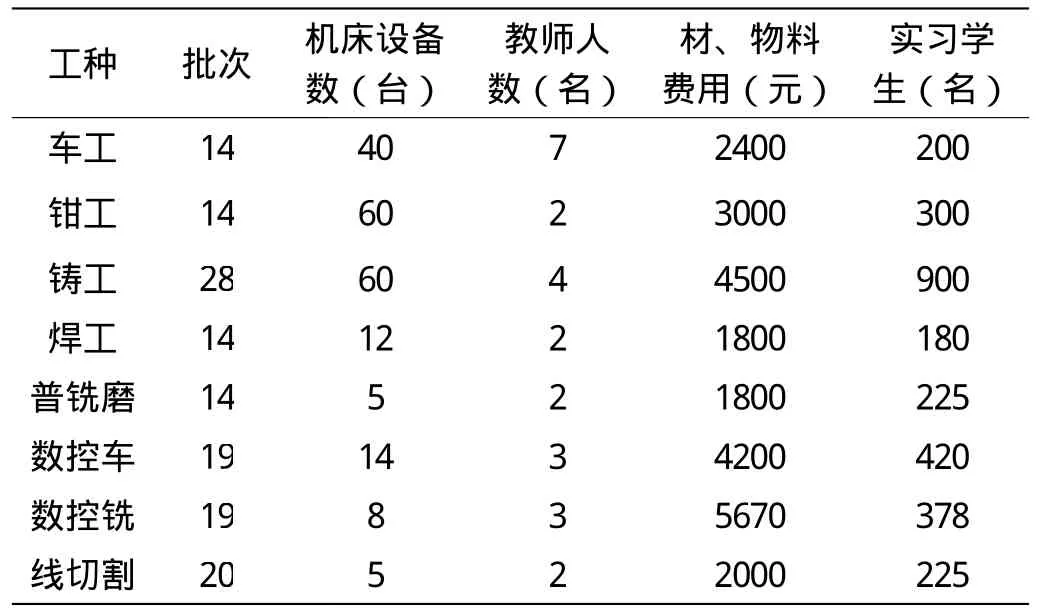
表6 金工實習資源配置表（規劃后）

通過表7可以看出，經過對金工實習中心實習資源的線性規劃，發現在這次投資中需要在鑄工增加60個工位，增加4臺數控車床，增加2臺數控銑床。另外還需要增加4名金工實習教師，其中鑄工兩名，數控車、數控銑各一名。在材料、物料的消耗上，每批學生需增加5070元，全年共需增加70 980元。通過這樣的投入，鑄工每批可承擔學生將增加450人，數控車每批可承擔學生將增加120人，數控銑每批可承擔學生將增加108人，按全年14批計算，共可增加9492人次參加金工實習。

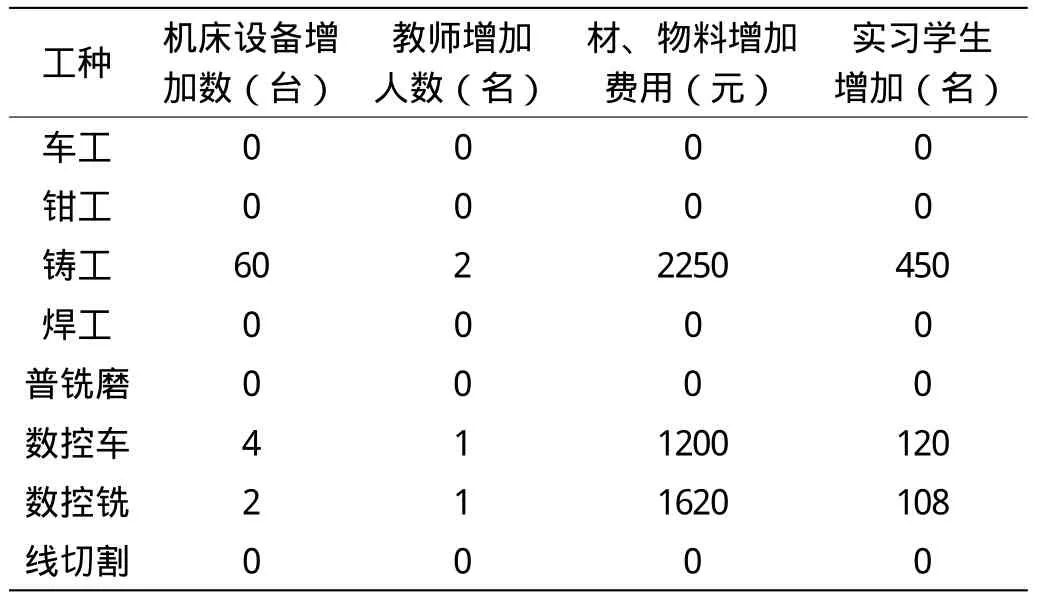
表7 金工實習資源配置變化表（規劃后）

結論 通過求解線性規劃模型，獲得南京工業大學金工實習資源優化的最佳結果。并依據此結果，可以得出，在此次對金工實習中心的投資中，應對鑄工、數控車、數控銑這三個工種進行設備、實習教師、材料費用等方面的加大投入，這樣，金工實習中心就能夠盡可能多地容納實習學生。

5 結束語

本文將理論和實際結合起來，通過建立金工實習中心實習資源線性規劃模型，運用線性規劃求解法中的單純形法求解，對實習設備、實習教師和實習所用機物料三種資源在各工種之間作了優化配置，并利用此結果，用新投入的資金購買資源對各工種進行合理配置。但是，由于單位機物料消耗成本，單位人工成本、設備成本、設備折舊都是根據以往的數據和經驗假設的，隨著物價水平等一系列因素的影響，其數值將不可避免地產生偏差，這也將會影響到線性規劃求解的準確性。

[1]錢頌迪.運籌學[M].北京:清華大學出版社,1995.

[2]吳清烈,等.運籌學[M].江蘇:東南大學出版社,2004.

[3]唐大超.應用線性規劃提高材料利用率[J].十堰職業技術學院學報,2007(12):100-104.

[4]鐘儀華.利用多約束水平線性規劃方法建立油田開發產量分配優化模型[J].石油規劃設計,2007(11):5-8.

[5]張學鮫.線性規劃在工期資源優化中的應用模型[J].建造技術,2009(1):49-51.