光滑帽子動態本構模型驗證及應用研究

劉俊新，楊春和，劉育田

(1.西南科技大學 土木工程與建筑學院,四川 綿陽 621010；2. 中國科學院 武漢巖土力學研究所 巖土力學與工程國家重點實驗室,武漢 430071)

鉆地武器指攜帶鉆地彈頭鉆入地下目標引爆的精確制導武器。該種武器鉆入地下目標過程及目標內部后的延時爆炸均涉及對目標組成部分在沖擊荷載作用下動力響應。目標主要由巖土介質與混凝土組成。對壓實黏土受沖擊荷載作用的動力響應在防護工程及武器設計中有重要意義。

在沖擊荷載作用下土體處于復雜應力狀態，土體自身特征導致其與金屬材料不同特性[1-3]，如：① 材料剪切破壞前會萌生大量微孔隙，引起體積變形增大而產生剪脹特性；② 材料應力-應變曲線及屈服強度表現出的明顯靜水壓力與應變率相關性；③ 強度不服從各向同性假定，抗拉強度遠低于抗壓強度；④ 土體內部的含大量水或不含水孔穴的力學行為十分復雜。為此提出各種理論模型描述土的力學性能。

為分析爆炸與沖擊荷載下土與結構物的相互作用，Schwer等[4-10]采用失效土壤與可壓扁泡沫本構模型、土/混凝土本構模型、地質帽子模型(*Mat _Geologic _Cap_Model)及連續光滑帽子模型等四種本構模型進行數值模擬。該四種模型均為與壓力相關的本構模型，只在描述剪切破壞時應力偏量第二不變量J2與壓力p 采用不同擬合關系。第一、二種本構模型并未考慮剪切面與硬化面銜接，用體積應變與壓力關系表述，且在較低靜水壓力狀態時數值迭代不穩定，其應用有一定局限性；第三種本構模型則克服第一、二種的不足，在p-q表示的子午平面上增加一個帽子面，考慮剪切面與硬化面銜接，但二者相接時存在一階不連續性，造成數值計算時收斂困難等；第四種本構模型基于Schwer 等[4]的光滑“cap”模型，克服第三種本構模型的不足，并引入Rubin縮比函數，考慮拉壓強度差異及基于duvaut-lions類粘性應變率效應及能量理論的軟化損傷效應。

國內對土體在沖擊荷載作用下動力學響應研究成果較少，所用本構方程大多為第一、二種，如劉彥等[11-12]的研究。理論上光滑帽子模型能較好描述土體動態力學性能，但實際應用如對侵徹深度影響驗證及不同本構模型、數值算法對侵徹深度影響尚未見報導。本文基于此進行研究。

1 光滑帽子模型

光滑帽子模型由地質帽子模型[4]發展而來。即將剪切屈服面與硬化帽子面用光滑曲線相連，克服因剪切面與硬化面相接時存在一階不連續造成數值計算收斂困難等問題，并考慮應力張量第三不變量、應變率效應、損傷軟化影響，見圖1。

圖1 光滑帽子模型二維示意圖[10]

1.1 應力不變量

屈服面由應力張量第一不變量I1、偏應力張量第二不變量J2及第三不變量J3表示。

1.2 塑性面

屈服面函數由三個應力不變量及帽子面硬化參數表示[4,10]為

(1)

式中：Ff為剪切屈服面；Fc為硬化帽子；R為Rubin應力縮放函數；κ帽子硬化參數，即帽子面與剪切面交點對應的I1值。

1.3 剪切破壞面

低圍壓下材料剪切破壞[4,10]可表示為

Ff(I1)=α-λexp-βI1+θI1

(2)

式中：α，λ，β，θ為由常規三軸壓縮試驗結果擬合的參數。

1.4 硬化面

由于地質材料應力-應變曲線在低圍壓下表現出軟化特征，高圍壓下表現出硬化特征，當材料處于由低圍壓至圍壓區域時，材料強度需結合帽子面及剪切面進行模擬。帽子模型由兩分段函數表示。處于低圍壓狀態時帽子函數為“1”；由低圍壓至高圍壓區域時帽子函數為橢圓，屈服函數完全依靠帽子面及剪切屈服面函數[4,10]，可表示為

Fc(I1,κ)=

(3)

帽子面硬化規律[4,10]表示為

D2(X(κ)-X0)2]}

(4)

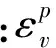
1.5 Rubin縮尺函數

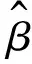
Q1=α1-λ1exp-β1I1+θ1I1

(5)

Q2=α2-λ2exp-β2I1+θ2I1

(6)

式中：α1,λ1,β1,θ1,α2,λ2,β2,θ2均為擬合參數。

1.6 損傷軟化

光滑帽子模型中含兩類損傷[14-15]，即應力張量第一應力不變量為壓應力時引入延性損傷使應力折減；應力張量第一應力不變量為拉應力時引入脆性損傷使應力折減。損傷應力定義為

(7)

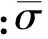
損傷累積受拉時用脆性損傷方程表示；受壓時用延性損傷方程表示。

1.7 單元侵蝕

損傷參數d趨近于1時，單元會失去強度及剛度。為防止因剛度減小導致的計算困難，單元可據用戶需要進行刪除或保留。d>0.99及最大主應變超出用戶設定值時，單元會被刪除。

1.8 粘塑性率效應

(8)

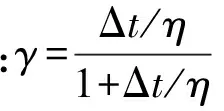
1.9 參數確定

光滑帽子模型參數主要通過靜水壓力試驗、常規三軸壓縮試驗、三軸拉伸試驗、單軸應變試驗、真三軸試驗及SHPB試驗確定。壓實度為95%、含水量12.54%(最大干密度γd,max=2.02 g/cm3，最佳含水量ωopt=12.87%)西南紅層泥巖粉碎土(土粒粒徑小于2 mm)的光滑帽子模型參數[6,16]見表1。

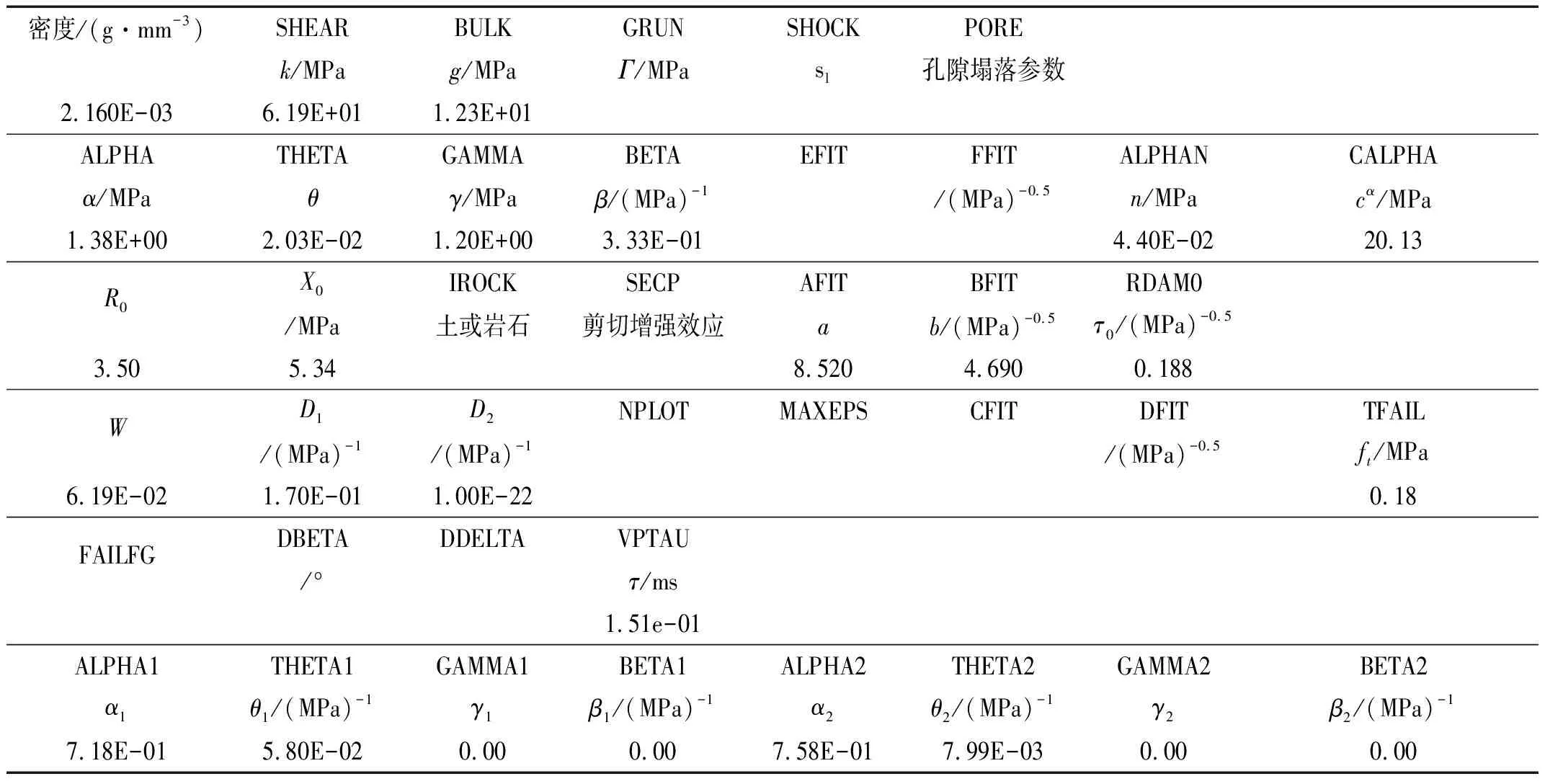
表1 光滑帽子模型參數

2 動態本構模型合理性分析

為論證提出的動態本構模型能正確反映土體本身力學性能進行彈丸侵徹試驗。采用數值模擬對彈丸侵徹試驗重演，并分析本構模型合理性。

2.1 彈丸侵徹試驗

試驗在空氣炮裝置上進行，土體壓實度為95%，含水率12.54%，外側用鋼筒約束，內徑尺寸為150 mm× 1 000 mm，壁厚5 mm，物理模型制備采用分層靜壓法。鋼質彈丸直徑9.52 mm，侵徹速度v=200～300 m/s。試驗試驗裝置包括靜力及空氣炮加載裝置等。彈丸侵徹及開坑統計結果見表2。由表2看出，侵徹深度隨侵徹速度增加而增加，無論速度大小均存在開坑現象，且開坑大小與速度相關。侵徹速度為202 m/s時其平均侵徹深度為37.06 mm、平均開坑直徑19.71 mm、平均開坑深度5.00 mm；侵徹速度為310 m/s時其平均值分別為58.92 mm、41.98 mm、10.38 mm。

2.2 數值模型

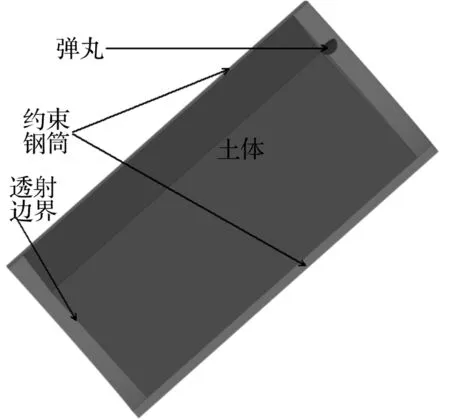
圖2 數值計算模型

計算模型取物理模型的1/4(無特殊說明，計算模型下同)，見圖2，土體高度200 mm，半徑75 mm，彈丸與約束鋼筒為剛性體，土體、彈丸及約束鋼筒均為Lagrange網格(土體完全損傷后自動刪除)，底部為透射邊界，彈丸與土體為侵蝕接觸，土體與約束鋼筒為面-面接觸，罰因子取2.0，土體壓實度95%，含水率12.54%，撞擊速度分202 m/s，310 m/s兩種，土體計算模型參數見表1。

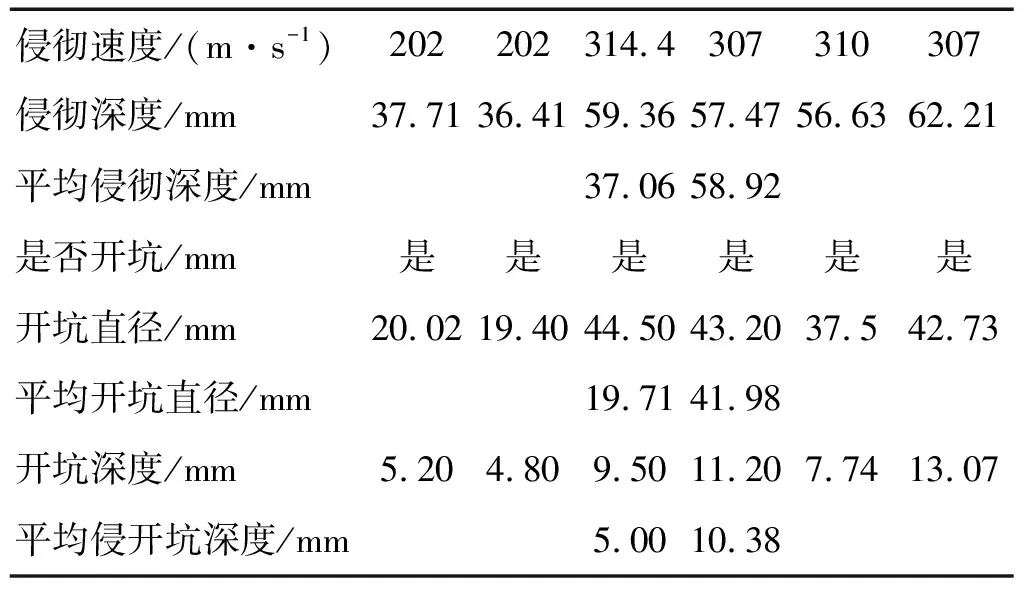
表2 侵徹情況統計表

整理后彈丸侵徹速度與深度關系曲線見圖3。由圖3看出，撞擊速度310 m/s、202m/s彈丸剩余速度25.79 m/s、40.24m/s時，其對應的侵徹深度為63.69 mm、44.74 mm；而模型試驗確定的侵徹深度為58.92 mm、37.06 mm，計算結果基本合理。

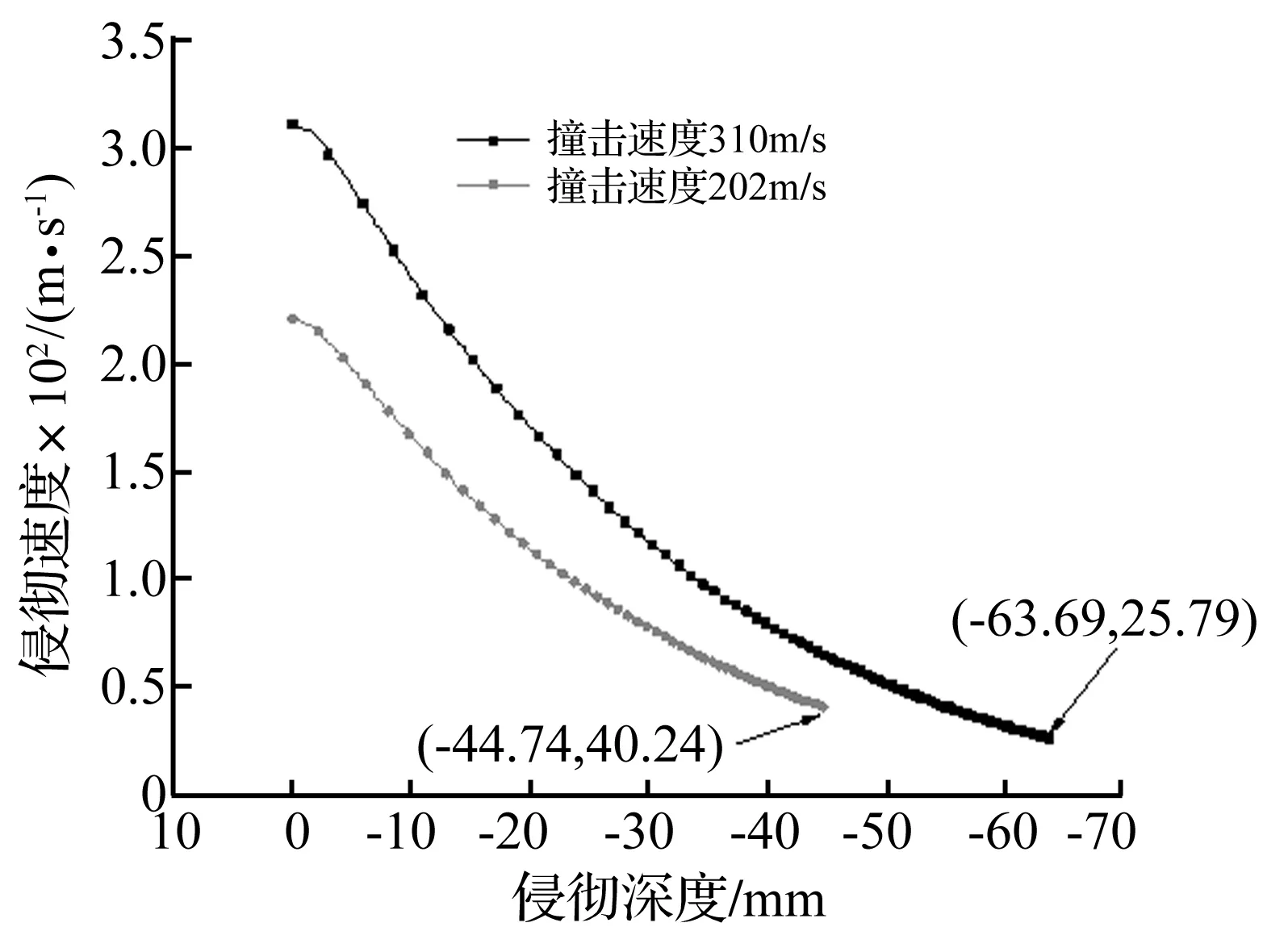
圖3 不同撞擊速度下彈丸侵徹數值計算結果

3 不同本構模型對計算結果影響

通常采用Drucker-Prager模型、土壤與泡沫模型(Soil_and_Foam)、光滑帽子模型(Schwer_Murry_Cap_ Model)分析土壤在沖擊荷載下的動力響應，其剪切屈服面采用不同擬合關系。

Drucker-Prager屈服面[17-18]為

(9)

Drucker-Prager模型的破壞曲面為圓錐體，其大小可通過α，k調整。據錐面與摩爾-庫倫受拉子午線相互關系可確定α，k[17-18]為

(10)

式中：φ為摩擦角；c為粘聚力。

Soil_and_Foam屈服面[17-18]為

(11)

式中：a0，a1，a2為擬合參數；p=I1/3。

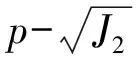
由以上分析知，光滑帽子模型考慮材料應變率效應、高圍壓下材料硬化及低圍壓下材料損傷軟化、應力狀態對屈服強度影響及壓力導致的塑性體積應變。應變率效應導致材料抵抗變形能力增大，而因材料硬化引入的帽子面、屈服面、材料損傷軟化及塑性體積應變導致材料抵抗變形能力減弱；土壤與泡沫模型及Drucker-Prager模型均為理想的彈塑性本構模型，其屈服面在π平面的形狀為圓形，均考慮因剪切破壞引起的剪脹效應而未考慮應力狀態對屈服面影響及應變率效應；兩模型不同處在于土壤與泡沫模型考慮壓力導致的塑性體積應變。因此為研究不同本構模型對侵徹過程影響，對彈丸侵徹試驗進行數值模擬，彈丸侵徹速度為310 m/s時計算模型同前，計算結果見圖6。由圖6看出，侵徹至相同深度時光滑帽子模型消耗能量最小，土壤與泡沫模型次之，Drucker-Prager模型最大，且土壤與泡沫模型與光滑帽子模型結果較接近，說明因材料硬化引入的帽子面、屈服面、材料損傷軟化及塑性體積應變導致材料抵抗變形能力減弱效應大于因應變率引起材料抵抗變形增強效應及塑性體積應變對侵徹深度影響。由于Drucker-Prager模型及土壤與泡沫模型對剪切面采用線性擬合，所致剪脹效應基本相同，但Drucker-Prager模型未考慮因壓力導致的土體積減小，因此Soil_and_Foam模型較Drucker-Prager模型引起的剪脹小(因屈服準則參數不同)，故侵徹阻力亦小。Drucker-Prager模型中當侵徹速度下降至54.8 m/s時，數值迭代出現不穩定。

圖4 土壤與泡沫模型剪切面擬合參數

表3 Drucker-Prage、土壤及泡沫、 光滑帽子模型剪切面參數統計表

4 不同數值算法對計算結果影響

由于土體破壞為延性破壞，與混凝土與巖石等脆性材料相比，殘余強度與峰值強度相差較小，土體在沖擊荷載作用下易發生大變形，破壞后土體對侵徹過程影響不可忽略。Lagrange算法中以物質坐標為基礎，網格單元依附于物質網絡，物質不會在單元與單元間發生流動。該方法優點為能精確描述結構邊界運動，但處理大變形問題時會出現嚴重的網格畸變現象。為使計算進行須采用網格刪除技術；Euler方法以空間坐標為基礎，劃分的網格及分析的物質結構相互獨立，網格在整個分析過程中始終保持最初的空間位置不動，在整個數值模擬中各迭代過程計算數值精度不變；但該方法在物質邊界的捕捉較困難, 用該方法時網格與網格間物質可流動；ALE兼具Lagrange方法與Euler方法特長，即在結構邊界運動的處理上引進Lagrange方法特點，因此能有效跟蹤物質結構邊界運動；在內部網格劃分上吸收Euler長處，即使內部網格單元獨立于物質實體而存在，但其又不完全與Euler網格相同，網格可據定義的參數在求解過程中適當調整位置，使網格不致出現嚴重畸變。此有利于分析大變形問題，用此方法時網格與網格間物質也可流動；SPH 算法優點為無需網格、無單元網格畸變問題，能模擬爆炸引起的大變形，在模擬炸藥爆炸物質飛濺方面更形象逼真；但SPH 算法精度不夠高、界面處理不成熟，對鄰粒子搜索需占用較多計算資源。

為研究不同數值算法對侵徹過程影響，對彈丸侵徹試驗進行數值模擬。彈丸侵徹速度310 m/s，計算模型同上，土體分別采用SPH、ALE及Lagrange網格，土體用光滑帽子模型為本構模型，參數見表1，計算結果見圖7。由圖7看出，在MM_ALE算法中侵徹曲線斜率逐漸變小又逐漸增大，隨侵徹速度減小，土體應變率效應逐漸減弱，說明土體抵抗變形能力變小；而當侵入到一深度時鋼筒約束作用逐漸增強，此時土體抵抗變形能力開始增大；而SPH，MM-ALE算法侵徹曲線斜率逐漸變緩，說明侵徹后期侵入深度相同，所需能量減小，與事實不符，其原因為Lagrange算法采用網格刪除技術，使其阻力減小；SPH算法雖未刪除粒子，但其計算精度較差。而采用Lagrange算法時適當提高罰因子可有效彌補因網格刪除導致的阻力減小，使侵徹深度達到合理范圍，但并未改變侵徹速度、深度總體變化趨勢。

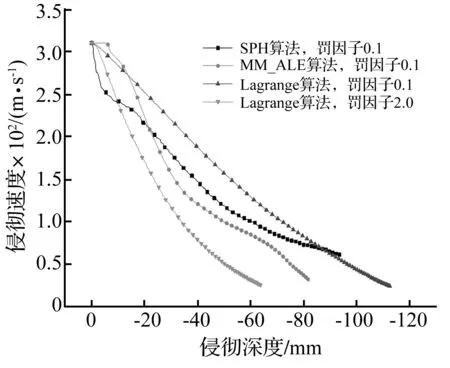
圖7 不同數值算法對侵徹過程影響

5 結 論

(1) 通過模型試驗與數值方法對彈丸侵徹試驗分析結果表明，光滑帽子模型能較好模擬在一定范圍內沖擊荷載作用下土體的動態力學響應。

(2) 侵徹到相同深度時光滑帽子模型消耗能量最小，土壤與泡沫模型次之，Drucker-Prager模型最大，土壤與泡沫模型與光滑帽子模型結果較接近。說明因材料硬化引入的帽子面、屈服面、材料損傷軟化及塑性體積應變導致材料抵抗變形能力減弱效應大于因應變率引起材料抵抗變形增強效應及塑性體積應變對侵徹深度影響。

(3) Drucker-Prager模型及土壤與泡沫模型對剪切面用線性擬合引起的剪脹效應基本相同，但Drucker-Prager模型未考慮因壓力導致土體積減小，Soil_and_ Foam模型較Drucker-Prager模型所致剪脹小(因屈服準則參數不同)，故侵徹阻力亦小。

(4) 在Drucker-Prager模型中侵徹速度下降到一定程度時，數值迭代出現不穩定。

(5) 采用MM-ALE算法，侵徹速度-侵徹深度曲線斜率基本開始逐漸變小，后又逐漸增大，而Lagrange算法及SPH算法曲線斜率逐漸變緩；SPH算法計算精度較差。

(6) 用Lagrange算法時適當提高罰因子可有效彌補因網格刪除導致的阻力減小，使侵徹深度達到合理范圍，但侵徹速度、深度總體變化趨勢未改變。

[1] 劉文韜.巖石含損傷本構模型和地下爆炸效應研究[D].合肥:中國科技大學,2002.

[2] 王志亮,鄭田中,李永池.巖石時效損傷模型及其在工程爆破中應用[J].巖土力學,2007, 28(8): 1615-1620.

WANG Zhi-lang, ZHENG Tian-zhong, LI Yong-chi. Time effect damage model of rock mass and its application to blasting engineering[J]. Rock and Soil Mechanics, 2007, 28(8):1615-1620.

[3] 勞俊.地下空腔解耦爆炸的數值模擬[D].合肥:中國科技大學,2008.

[4] Schwer L E,Murray Y D. A three-invariant smooth cap model with mixed hardening[J].International Journal for Numerical and Analytical Methods in Geomechanics,1994(18): 657-688.

[5] Fossum A F,Fredrich J T. Cap plasticity models and compactive and dilatant pre-failure deformation[J].Proceedings of the Fourth North American Rock Mechanics Symposium, 2000(7): 1169-1176.

[6] Livermore software technology corporation (lstc). Ls-dyna? keyword user’s manua[M]. Livermore: Livermore Software Technology Corporation, 2009.

[7] Katona M G,Mulert M A. A viscoplastic cap model for soils and rocks[C].//Proceedings of the International Conference on the Constitutive Laws for Engineering Materials. New York, NY: John Wiley & Sons Ltd., Mechanics of Engineering Materials, 1984: 335-350.

[8] Murray Y D. Numerical simulation of damage in concrete[R]. Alexandria: APTEK, Inc, Technical Report DNA-TR-94-190, Prepared for the Defense Nuclear Agency under Contract DNA 001-91-C-0075, 1985.

[9] Sandler I, dimaggio F L,Barron M L. An extension of the cap model: inclusion of pore pressure effects and kinematic hardening to represent an anisotropic wet clay[C].//Proceedings of the International Conference on the Constitutive Laws for Engineering Materials. New York, NY: John Wiley & Sons Ltd., Mechanics of Engineering Materials, 1984: 547-560.

[10] Schwer L E. Continuous surface cap model for geomaterial modeling: a new ls-dyna material type[C].// Proceedings of the 7th International LS-DYNA Users Conference, Dearborn, Michigan: LSTC & ETA, 2002: 16-50.

[11] 劉彥,黃風雷,張振宇. 土壤覆層對混凝土中爆炸毀傷破壞的影響[J]. 北京理工大學學報, 2007,27(9):765-768.

LIU Yan, HUANG Feng-lei, ZHANG Zhen-yu. Influence of soil cladding on explosion in concrete[J]. Transactions of Beijing Institute of Technology, 2007, 27 (9):765-768.

[12] 李小雷. 土壤混凝土分層介質中爆炸的數值模擬[D].長沙:國防科技大學,2006.

[13] Simple R M.Convenient isotropic failure surface[J].Journal of the Engineering Mechanics Division, American Society of Civil Engineers, 1991(117): 348-369.

[14] Simo J C, Ju J W. Strain and stress based continuum damage models-Ⅰ formulation[J]. International Journal of Solids and Structures, 1987, 23(7):821-840.

[15] Simo J C, Ju J W. Strain and stress based continuum damage models-Ⅱ computational aspects[J].International Journal of Solids and Structures, 1987, 23(7): 841-869.

[16] 劉俊新.壓實粘性土動態力學性研究[R].四川:中國工程物理研究院總體工程研究所,2011.

[17] 鄭穎人,沈珠江,龔曉南.巖土塑性力學原理[M].北京:中國建筑工業出版社,2002.

[18] 高紅,鄭穎人,馮夏庭. 巖土材料能量屈服準則研究[J].巖石力學與工程學報, 2007, 26(12): 2437-2443.

GAO Hong, ZHENG Ying-ren, FENG Xia-ting. Study on energy yield criterion of geomaterials[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2437-2443.