裝有腹板式鋼制防屈曲支撐框架結構振動臺試驗及分析

郝曉燕，李宏男，牧野俊雄

(1.大連理工大學 建設工程學部，遼寧 大連 116023； 2.日本住金關西工業株式會社，日本 東京)

支撐為建筑結構中常見抗側力構件，防屈曲支撐則為特殊支撐形式，隸屬消能減震技術領域，由鋼內芯、外包約束構件及兩者間無粘結材料或間隙三部分組成。支撐軸力由鋼內芯承擔；外包約束構件不提供軸力，僅對內芯側向變形進行約束防止支撐受壓時發生屈曲；鋼內芯與外包約束構件用無粘結材料或空隙隔離，以確保內芯獨自承擔軸向力。防屈曲支撐在風荷載及小震作用下與普通支撐相同，可作為建筑結構的抗側力構件；在中震、大震作用下能克服普通支撐受壓屈曲缺點，拉壓恢復力特性基本一致，不會出現強度、剛度退化，具有更飽滿的滯回曲線，且隨結構側向變形及層間位移的增大產生較大阻尼消耗輸入的地震能量，迅速衰減結構振動反應；強震中保護主體結構及構件免遭破壞。可見防屈曲支撐亦為性能優越的耗能構件。防屈曲支撐以經濟性、實用性在工程抗震領域獲得廣泛認可[1-4]，且形式多種多樣，Fujimoto等[5-6]分別研究內核單元為一字板、約束單元為矩形鋼管、四鋼管的防屈曲支撐性能；李妍等[7]研究一字形內芯外包鋼管的防屈曲鋼支撐阻尼器；周云等[8]提出“開孔式”、“開槽式”防屈曲支撐；高向宇等[9-11]分別提出組合熱軋角鋼防屈曲支撐及型鋼組合裝配式防屈曲支撐。

振動臺試驗能真實再現地震過程，為目前研究結構抗震性能及地震反應、破壞機理最準確試驗方法、最直接方法。諸多對裝有防屈曲支撐的框架結構進行振動臺實驗[12-14]，僅研究防屈曲支撐的減震效果，而與普通支撐減震效果進行對比研究較少，不能體現防屈曲支撐的優越性。文獻[15-16]提出腹板式鋼制防屈曲支撐(簡稱SUB)，并進行擬靜力試驗及數值模擬。為檢驗其動力荷載下力學性能，本文對裝有防屈曲支撐及普通支撐的鋼框架結構進行模擬振動臺試驗，比較兩種支撐的減震效果，驗證腹板式鋼制防屈曲支撐的耗能能力。

1 振動臺實驗

1.1 框架模型設計

試驗在大連理工大學國家重點實驗室-抗震研究室模擬地震臺上進行。試驗模型為雙跨3層鋼框架見圖1，底面尺寸1.5 m×1.8 m，層高0.9 m。框架柱及框架梁分別由40 mm×40 mm×4 mm、60 mm×40 mm×4 mm矩形鋼管焊接而成，斜撐用30 mm×30 mm×3 mm等邊角鋼，結構底部與基礎嵌固，梁、柱間剛性連接。結構首層層間剛度較小，層間位移變形較大，故在結構首層安裝2個SUB，2、3層加普通支撐40 mm×40 mm×3 mm角鋼。為增大框架對地震波反應，在每層樓板放置1900 kg質量塊，2、3層放置1830 kg質量塊。安裝SUB框架結構模型(模型A)及安裝普通支撐的框架結構(模型B)局部放大圖見圖2。

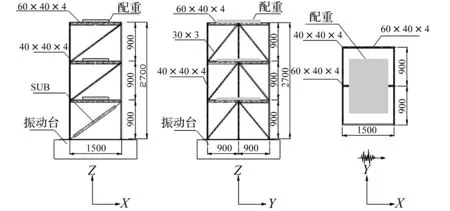
圖1 結構平面及立面簡圖

圖2 SUB鋼框架結構及普通支撐鋼框架

1.2 SUB模型及節點連接

SUB試件構造見圖3，尺寸及材性試驗數據見表1。SUB屈服荷載理論值為Py=σyAG=19 200 N，其中σy為芯材屈服強度(128 MPa)，AG為屈服段截面面積，彈性剛度據內核構件各部分截面面積及長度用串聯剛度法計算，即

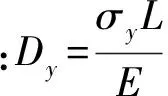
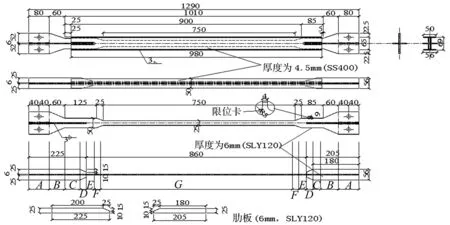
圖3 SUB示意圖及尺寸

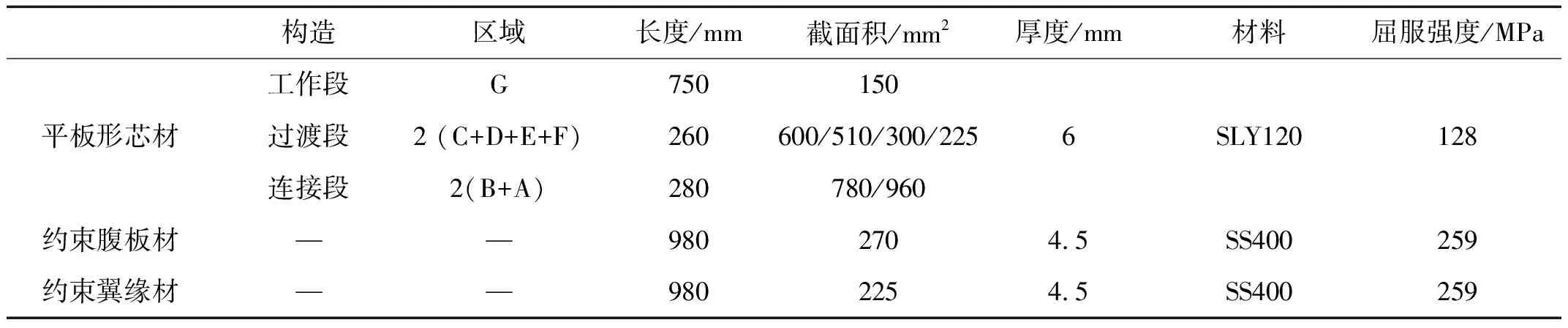
表1 SUB尺寸及材料參數

圖4 SUB及普通支撐與節點板連接方式

將圖3中數據代入上式，得SUB屈服位移Dy=0.826 mm，彈性剛度K=32 922 N/mm，與試驗結果接近[16]。

將第1層防屈曲支撐換成普通支撐，并與SUB在相同軸力下屈服，得普通支撐尺寸為L36 mm×36 mm×3 mm。SUB與普通支撐均通過螺栓與節點板連接，見圖4。

1.3 加載及試驗方案

先進行SUB框架結構模擬振動臺安裝試驗,因該結構在大震作用下SUB屈服耗能，框架層間變形較小，可保證鋼框架在試驗中保持彈性變形。再將第一層SUB卸除換成普通支撐，進行普通支撐框架結構模擬振動臺試驗。由于鋼框架處于彈性變形，普通支撐框架結構試驗時鋼框架仍可重復利用。地震動沿與SUB平面平行方向輸入。用白噪聲激振以識別結構自振模態，白噪聲波因頻譜(0～100 Hz)較寬，可激起結構各階響應，通過對時域信號進行傳遞函數變換為頻域信號，可識別各工況的結構動力特性。分別對SUB框架結構及普通支撐框架結構兩種工況進行地震動作用下動力反應試驗。考慮不同場地對減震效果影響，選三條典型地震波即遷安波南北分量、TaftN21E分量及唐山波(15～45 s間部分)，見表2。地震峰值由0.1 g開始，按0.05 g逐級加載，加載到0.6 g，普通支撐框架加載到0.5 g。通過振動臺面的加速度傳感器記錄臺面的加速度信號。在沿高度各層中間橫梁處安裝加速度傳感器，記錄加速度反應。

表2 地震波選用

1.4 SUB框架結構與普通支撐框架結構對比分析

對比SUB框架結構與普通支撐框架結構在相同地震記錄峰值作用下位移反應，可鑒定SUB對結構位移反應的控制效果。三種地震記錄(峰值加速度0.1 g，0.2 g，0.4 g)激震下模型A、B最大位移反應及不同地震記錄、不同峰值加速度下SUB減震效果見表3。兩種框架在遷安波地震記錄下首、頂層位移反應時程曲線見圖5。兩種框架結構在Taft波地震作用下首、頂層位移反應時程曲線見圖6。由表3、圖5、圖6看出，相同峰值加速度作用下與普通支撐框架層間位移相比，SUB框架層間位移有不同程度減小；在小震作用下SUB及普通支撐框架結構層間位移基本相同，此因主體結構保持彈性變形，SUB未達屈服荷載，未進入耗能階段，此時與普通支撐作用相同，僅為主體結構提供剛度；隨地震峰值增加，普通支撐框架結構層間位移遠大于SUB框架結構，此因SUB在主體結構進入彈塑性變形前進入工作耗能，此時表現較強非線性，而普通支撐通常由失穩控制在中震、大震作用下會發生整體失穩或局部屈曲，導致樓層剛度及承載力突降，顯著降低結構的延性及耗能能力,影響結構抗震安全性。因此，SUB較普通支撐對結構首層層間位移及頂層位移控制效果均較好；但因SUB安裝于第一層，數量較少，故對底層控制效果更明顯。

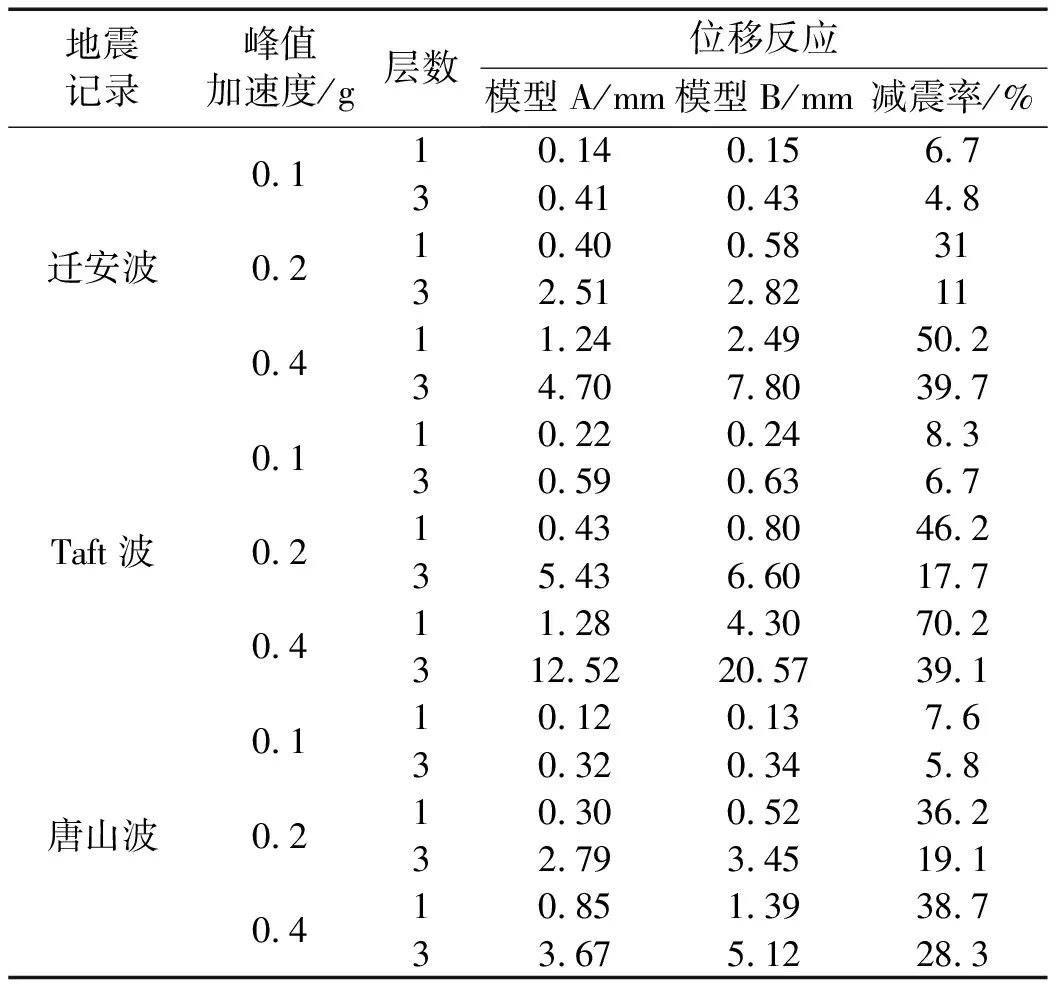
表3 結構位移反應及減震率

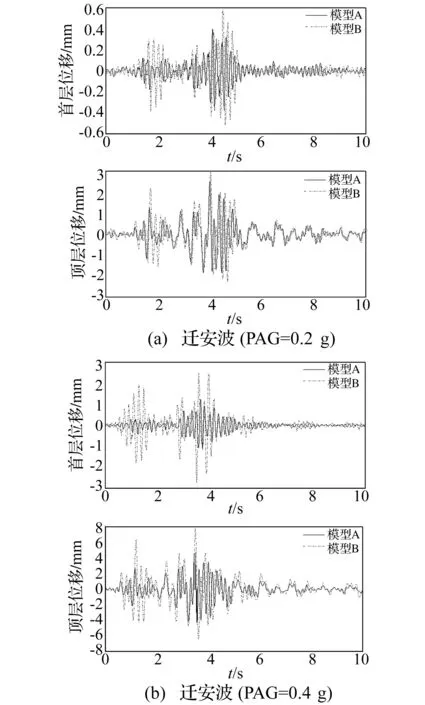
圖5 普通支撐框架結構與SUB框架結構在遷安波作用下位移時程曲線

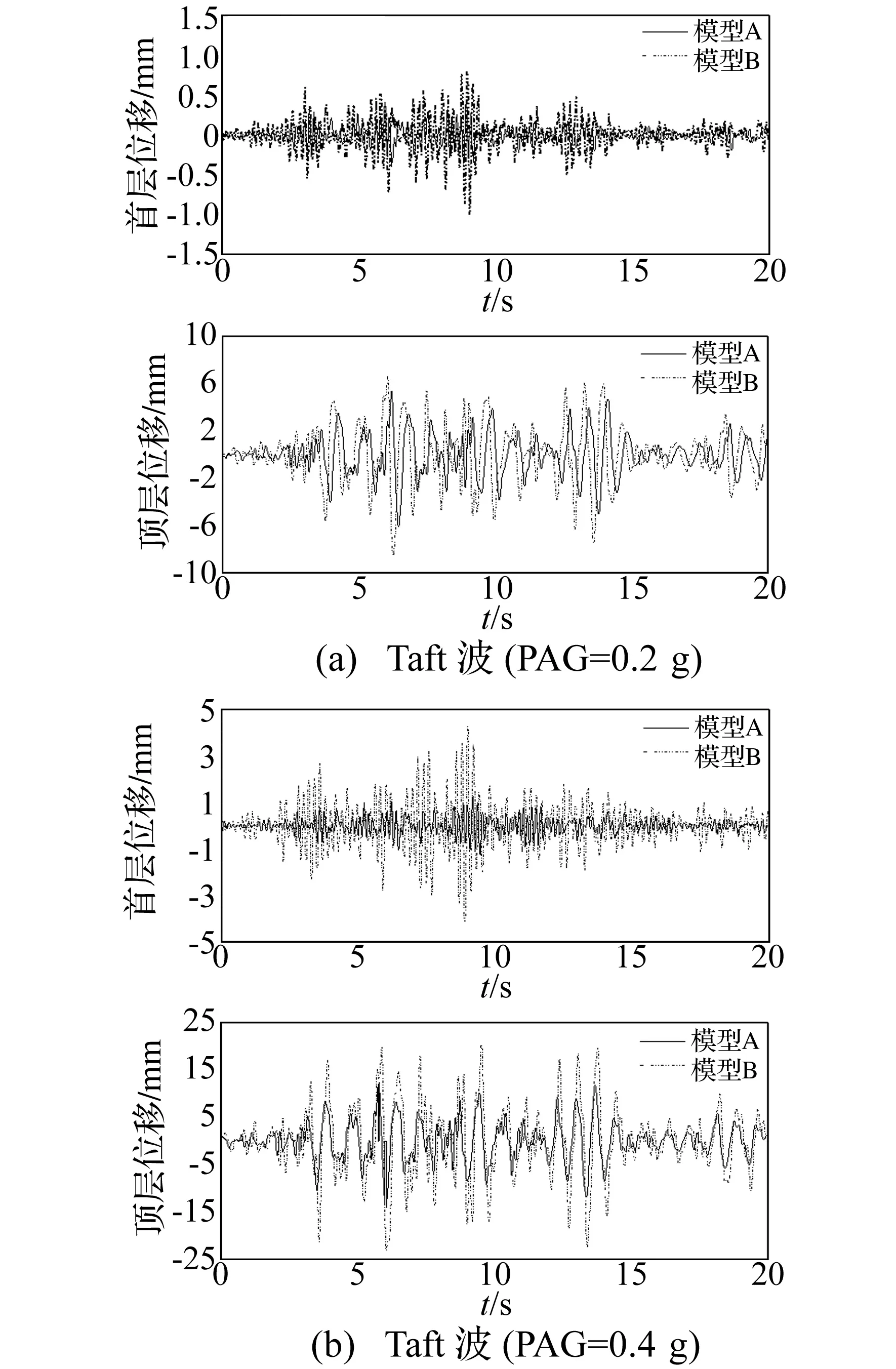
圖6 普通支撐框架結構與SUB框架結構在Taft波作用下位移時程曲線

2 數值分析

2.1 有限元模型建立

用有限元分析軟件對防屈曲支撐框架結構體系分析時，防屈曲支撐用非線性連接單元實現。本文選塑性連接Bouc-Wen模型模擬。Bouc-Wen恢復力模型非線性力-變形關系表達式[17]為

p(t)=αbKEd(t)+(1-αb)KEz(t)

βbν(t)|z(t)|n+Aν(t)

式中：P為防屈曲支撐軸向力；KE為控制初始剛度參數；d為SUB軸向變形；γb，βb，A，n為滯回常數。γ，β，A決定滯回曲線大小及形狀；n決定曲線光滑程度，無窮大時為雙線性模型。

模型建立過程中將底層柱剛性固結于地面，結構整體阻尼比取0.02，SUB軸向屈服力19.2 kN、彈性剛度33.292 N/mm，第二剛度系數為0.05，屈服指數3，沿X方向輸入地震波。

2.2 試驗與數值模擬模擬結果對比

振動臺試驗時用白噪聲掃描整個框架，獲得結構自振頻率為9.0 Hz。數值模擬時地震波用振動臺實驗時臺面采集的地震波峰值。對結構模型進行模態分析，獲得結構自振周期為0.107 94 s，即結構自振頻率為9.2 Hz，與試驗結果吻合較好。SUB框架結構在遷安地震波(峰值加速度為0.2 g)激勵下試驗數據與數值計算結果對比曲線見圖7。普通支撐框架結構在遷安地震波(峰值加速度0.2 g)激勵下，試驗數據與數值計算結果對比曲線見圖8。激震下普通支撐及防屈曲支撐框架結構在遷安波作用下試驗及數值模擬結果最大位移反應及兩者間誤差見表4。由圖7、圖8及表4看出，有限元計算結果與試驗結果逼近較好，為此類SUB框架設計與工程分析提供可行的計算方法。

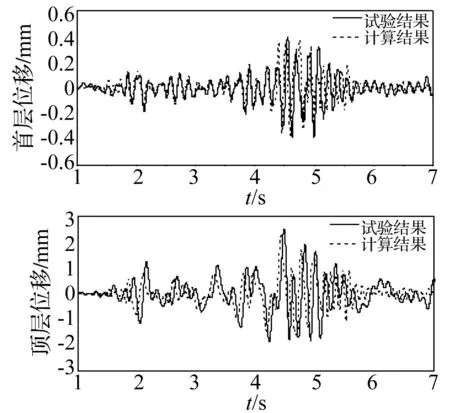
圖7 SUB框架結構在遷安波作用下位移

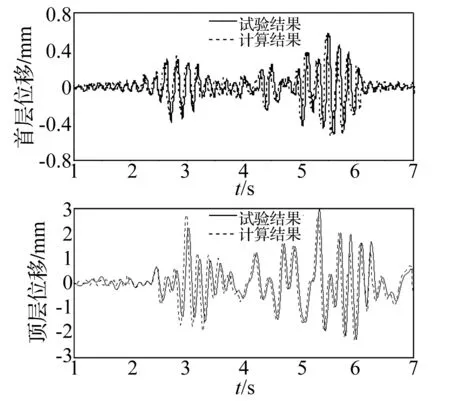
圖8 普通支撐框架結構在遷安波作用下位移

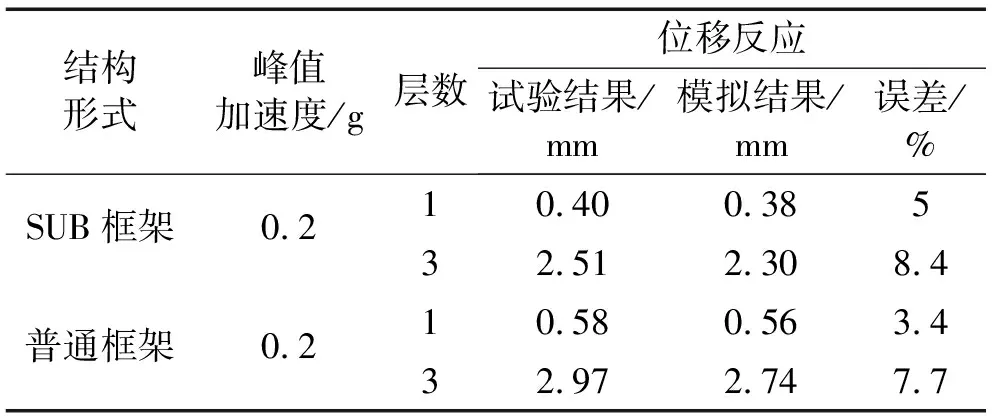
表4 結構在遷安波作用下試驗與模擬結果對比

3 結 論

本文對裝有腹板式鋼制防屈曲支撐及普通支撐框架結構模擬地震振動臺試驗及相關理論分析。比較兩種支撐減震效果，用有限元方法對振動臺試驗數值計算，結論如下：

(1) 模擬地震振動臺模型試驗及理論分析均表明，本文所提SUB在小震作用下與普通支撐相似，僅為框架結構提供初始剛度，而在中震或大震作用下SUB在主體結構進入彈塑性變形前進入工作耗能，可極大減小結構反應。

(2) 數值模擬為分析、設計消能減震結構基礎，對加SUB與普通支撐框架結構振動臺試驗數值模擬結果表明，SUB兼具中心支撐及位移性阻尼器功能，為一類理想的消能裝置。

[1] 周云.防屈曲耗能支撐結構設計與應用[M].北京:中國建筑工業出版社,2007.

[2] 楊昌民,牧野俊雄,李宏男.防屈曲支撐的研究進展及其工程應用[J].建筑科學與工程學報,2011,28(4):75-85.

YANG Chang-min, Makino Toshio, LI Hong-nan. Research progress and its engineering application of buckling-restrained brace[J]. Journal of Architecture and Civil Engineering,2011, 28(4):75-85.

[3] 周云,唐榮,鐘根全，等.防屈曲耗能支撐研究與應用的新進展[J]. 防災減災工程學報,2012,32(4):393-407.

ZHOU Yun, TANG Rong, ZHONG Gen-quan,et al. State-of-the-art and state-of-the-practice of buckling-restrained brace [J]. Journal of Disaster Prevention and Mitigation Engineering, 2012, 32(4):393-407.

[4] Anidya D, Ronald O H. Case study of a 40-storey buckling-restrained braced frame building located in los angeles [J]. The Structural Design of Tall and Special Buildings, 2010, 19(1/2): 77-93.

[5] Fijumoto M A. Study on the unbonded brace encased in buckling-restraining concrete and steel tube[J]. Journal of Structural and Construction Engineering,1988 (34B):249-258.

[6] Koetaka Y, Narihara H. Experimental study on buckling restrained braces[C]. Proceedings of Sixth Pacific Structural Steel Conference, Beijing, 2001.

[7] 李妍,吳斌.防屈曲支撐阻尼器的實驗研究[J].土木工程學報, 2006, 39(7):9-14.

LI Yan, WU Bin. An experimental study of anti-buckling steel damping-braces[J]. China Civil Engineering Journal, 2006, 39(7): 9-14.

[8] 周云,錢洪濤. 新型防屈曲耗能支撐設計原理與性能研究[J].土木工程學報,2009, 42(4):64-71.

ZHOU Yun, QIAN Hong-tao. A study on the design principle and performance of a new type of buckling-resistant brace[J]. China Civil Engineering Journal, 2009,42(4):64-71.

[9] 高向宇,張慧,杜海燕,等.組合熱軋角鋼防屈曲支撐構造及抗震試驗[J].北京工業大學學報,2008,34(5):498-504.

GAO Xiang-yu, ZHANG Hui,DU Hai-yan,et al. Experiment on conformation and seismic performance of bucking-restrained brace made of composed hot-rolled angle steel [J]. Journal of Beijing University of Technology,2008,34(5): 498-504.

[10] 高向宇,王永貴,劉丹卉. 端部加強型組合熱軋角鋼防屈曲支撐靜載試驗研究[J].建筑結構學報,2010,31(3):77-82.

GAO Xiang-yu, WANG Yong-gui, LIU Dan-hui. Static tests on buckling restrained brace made of hot-rolled steel angle with strengthened ends[J]. Journal of Building Structure, 2010, 31(3): 77-82.

[11] 郭彥林,江磊鑫.型鋼組合裝配式防屈曲支撐性能及設計方法研究[J].建筑結構,2010, 40(1):30-37.

GUO Yan-lin, JIANG Lei-xin. Behavior and application of buckling-restrained braces assembled with section steels[J]. Building Structure,2010, 40(1):30-37.

[12] 孔祥雄. 新型屈曲約束支撐抗震性能研究[D]. 北京:中國建筑科學研究院,2009.

[13] Castellano M G, Balducci F, Antonucci R. Shaking table tests on R.C. frame with dissipative bracings[C]. Seismic Engineering Conference, 2008:1358-1365.

[14] CHEN Cheng-cheng. Recent advances of seismic design of steel building in taiwan[C]. International Training Programs for Seismic Design of Building Structures, 2002.

[15] 楊昌民,李宏男,牧野俊雄,等. 防屈曲支撐的有限元模擬與滯回性能分析[J]. 防災減災工程學報,2012,32(2):145-151.

YANG Chang-min, LI Hong-nan, TOSHIO Makino,et al. Finite element simulation and hysteretic-performance analysis of buckling-restrained braces[J]. Journal of Disaster Prevention and Mitigation Engineering,2012,32(2):145-151.

[16] 郝曉燕,李宏男,楊昌民,等. 腹板式鋼制防屈曲支撐力學性能試驗研究[J]. 振動工程學報, 2012, 25(5): 497-505.

HAO Xiao-yan, LI Hong-nan, YANG Chang-min, et al. Experimental investigation of seismic performance of an innovative H type steel-unbuckling-brace[J]. Journal of Vibration Engineering, 2012,25(5): 497-505.

[17] Ma F, Bockstedte A, Foliente G C, et al. Parameter analysis of the differential model of hysteresis[J].Journal of Applied Mechanics,ASME, 2004,71(3):342-349.