基于功率譜靈敏度分析的結構損傷識別方法
鄭澤棟,陳偉歡,呂中榮,劉濟科
(中山大學 工學院 應用力學與工程系,廣州 510006)
基于振動結構損傷檢測方法具有非破壞性、快速、方便等優點,已廣泛應用于結構狀態評估與損傷識別[1]。其中基于靈敏度分析的損傷識別算法被認為較有效。通過建立模態頻率及振型[2-3]、附加質量[4]、自回歸系數[5]、頻響函數[6]或結構動態響應[7-8]等可對結構單元剛度靈敏度矩陣求解結構損傷位置及損傷程度。然而此類算法[2-5]大多停留在少量參數(如模態頻率)對結構參數靈敏度分析,必會丟失諸多有效信息,較難適應于高自由度多參數的復雜結構。基于頻響函數靈敏度分析方法需同時已知激勵及響應信息,而實際中激勵卻未知。基于響應靈敏度分析的時域損傷識別算法[7-8]能有效避開以上缺點;但時域響應具有偶然性,對隨機環境振動激勵下土木工程結構應用較困難。
本文研究基于功率譜靈敏度分析的損傷識別算法,先將激勵譜參數化,利用隨機振動虛擬激勵法獲得平穩隨機激勵下結構響應功率譜密度函數對結構損傷參數及激勵譜參數的靈敏度,采用有限元模型修正實現結構損傷識別與激勵譜識別。經剪切結構損傷識別數值結果表明,該方法僅用有限個傳感器頻域數據,亦能較好識別結構損傷及激勵譜。
1 隨機振動虛擬激勵法
虛擬激勵法[9]為隨機振動領域突破性發展,對推進隨機振動成果實用性具有重要意義,已廣泛用于求解大型土木結構的隨機地震響應、風激隨機響應及車輛結構優化[10]等。本文討論的隨機激勵主要為多點完全相干平穩激勵,暫不考慮其它復雜情況。
1.1 結構單點平穩激勵
線性系統受自譜密度Sff(ω)單點平穩隨機激勵f(t)時,響應x自功率譜Sxx(ω)為
Sxx=|H|2Sff
(1)
式中:H為頻率響應函數,表示為
x=Heiωt
(2)
(3)
由式(3)應有
(4)
式中:*表示共軛。
由此獲得結構隨機響應功率譜。響應與激勵間關系為線性,虛擬激勵法即能應用。上式未對輸入、輸出量進行限制,即激勵可以是位移、速度、加速度或外力、扭矩等,響應則可任意為位移、內力或應變等。
1.2 結構多點完全相干平穩激勵
結構隨機地震響應、風激隨機響應等均屬結構受多點完全相干平穩激勵情形,此可視為廣義單激勵問題,將以上方法稍加推廣即可簡單解決。
在頻域中求解線性結構平穩隨機響應的傳統公式為
Sxx=H*SffHT
(5)
式中:Sff為已知激勵譜矩陣;H為傳遞函數矩陣;Sxx為待求響應譜矩陣;上標*,T分別表示矩陣共軛及轉置。
Sff可分解為
Sff=a*aTS0
(6)
構造虛擬簡諧激勵為
(7)
求出簡諧響應x,即
x=beiωt
(8)
則
Sxx=x*xT=b*bT
(9)
(10)
所以
(11)
從而
b*bT=H*a*aTS0HT=H*SffHT
(12)
比較式(5)、(12)即可證明式(9)。
2 基于功率譜靈敏度分析的損傷識別方法
多自由度結構受迫振動有限元方程為
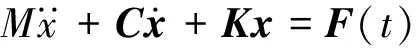
(13)
式中:M,K,C分別為系統質量矩陣、剛度矩陣、阻尼矩陣。阻尼矩陣采用Rayleigh阻尼模型[11],即
C=a1M+a2K
(14)
2.1 響應功率譜對損傷參數靈敏度
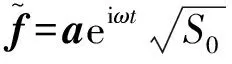
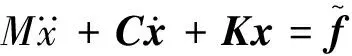
(15)
式(5)為結構受簡諧激勵受迫振動,結構簡諧響應可由式(8)、(11)求得。為求得結構簡諧響應對結構損傷參數αi的靈敏度,式(15)兩邊對損傷參數求偏導,即
(16)
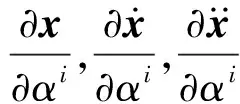
式(16)右邊可寫成簡諧激勵形式為
(17)
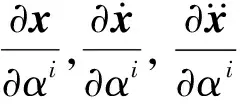
結構響應可寫為
x=(c+d)eiωt
(18)
(19)
(20)
結構簡諧響應對損傷參數的靈敏度可寫為
(21)
(22)
(23)
響應功率譜可寫為
Sxx=x*xT=c2+d2
(24)
(25)
(26)
響應功率譜對結構損傷參數靈敏度為
(27)
(28)
(29)
2.3 損傷參數識別
為尋找損傷參數αi使計算的響應功率譜與測量的響應功率譜匹配最好,即
δR=Sαδα
(30)
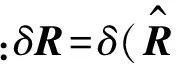

(31)
損傷參數增量向量δα可直接用最小二乘法求得:
(32)
實際損傷檢測中,直接用最小二乘法一般不能獲得有界解,因而得不到有效解,但采用阻尼最小平方法可獲得有效、有界解[12]為
(33)
式中:λ為正則化參數,本文用L曲線方法[13]獲得該參數最優。
修正后損傷參數向量為
α=α0+δα
(34)
式中:α0為無損傷時結構損傷參數向量。
2.4 損傷參數與激勵譜參數識別迭代算法
對激勵譜、結構未損模型及結構損傷后測量響應功率譜(以加速度響應功率譜為例)已知時,識別結構損傷參數可通過迭代步驟獲得:
(1) 由式(26)計算給定激勵譜下初始結構(無損傷結構)的響應功率譜,由式(29)計算響應功率譜對損傷參數的靈敏度,形成靈敏度矩陣;
(2) 用式(30)獲得測量響應功率譜與計算響應功率譜差值δR;
(3) 由式(33)計算損傷參數增量δα并利用式(34)計算修正后的損傷參數α;
(4) 重復(1)~(3),直至前后兩步增量δα達到較小誤差容許值:
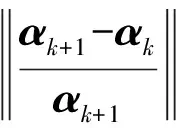
(35)
3 數值算例
考慮15自由度集中質量剪切模型見圖1,每層集中質量2×104kg,每層剪切剛度3.23×104kN/m,前兩階阻尼比取0.02。損傷模擬設為每層剛度折減,即
Ei=(1+αi)E
(36)
式中:Ei,αi,E分別為損傷模型第i個單元剪切剛度、損傷參數及完好模型剪切剛度。單元損傷參數代表單元損傷程度。
設結構受平穩地面加速度地震激勵,激勵譜設為過濾白譜,其自譜為
(37)
式中:ωg=15.708 s-1為土壤參數;ζg=0.6;S0=0.001 574 m2s-3。
結構未損與損傷后前10階固有頻率見表1。由表1看出,結構固有頻率在損傷后有所降低,但不明顯。本章僅利用第1、7、15三個節點加速度響應功率譜進行損傷檢測。由于實測中往往只能較準確測量到結構前幾階固有頻率,故加速度響應功率譜頻域僅取5 Hz以下進行檢測,分辨率為0.02 Hz,即100個頻點,表1中只覆蓋前4階固有頻率。本文暫不考慮從實測時程信號到響應功率譜變換過程中噪音、誤差。此處Tolerance取10-10。

圖1 剪切模型
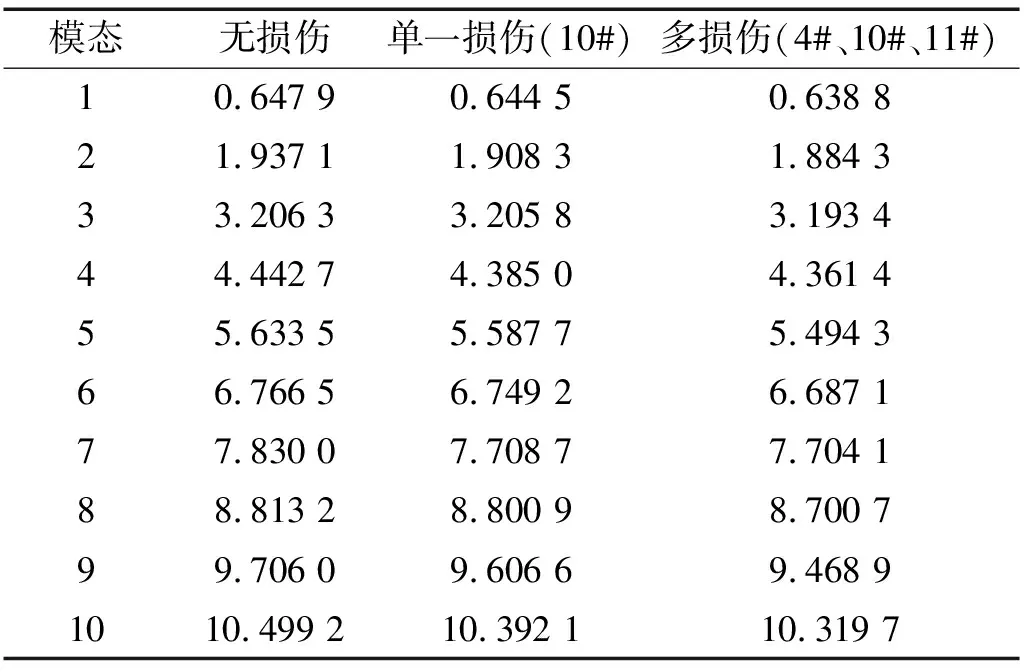
表1 有無損傷時系統前10階固有頻率(Hz)比較
3.1.1 單一損傷檢測
設結構第10個單元剛度出現20%折減。經29次迭代結果見圖2。圖2表明結構的單一局部損傷已成功檢測到,且未出現誤判現象,檢測誤差為0%。該算例表明激勵譜已知時,本文方法能成功檢測出結構單一局部損傷。
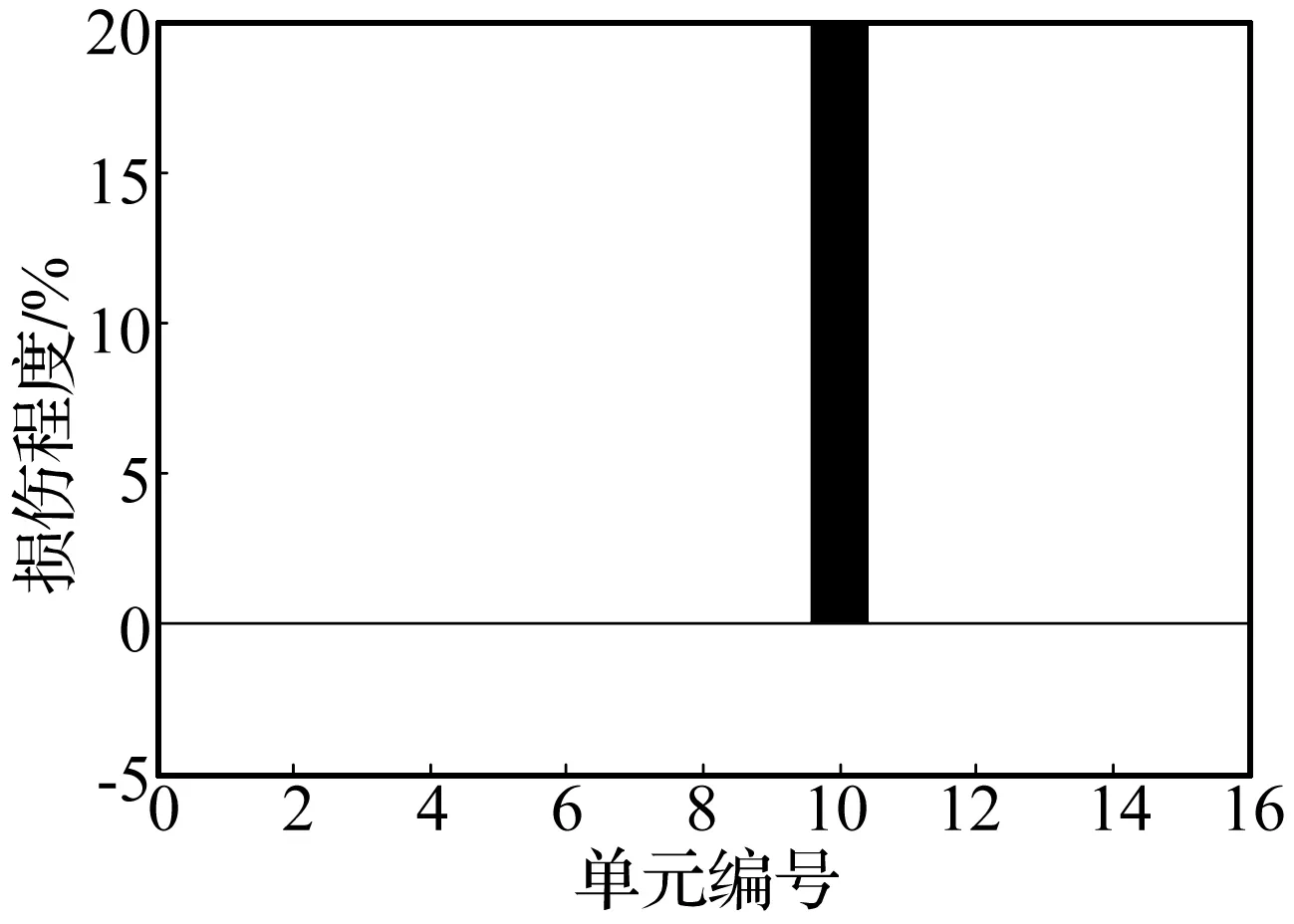
圖2 單一損傷檢測
3.1.2 多損傷檢測
設結構第4、10、11個單元剛度分別出現10%、20%、15%折減。經24次迭代結果見圖3。圖3表明結構的局部損傷已成功檢測到,且未誤判,檢測的最大誤差為0.3%,其它無損單位最大誤差為0.4%。該算例表明在激勵譜已知情況下本文方法能成功檢測出結構多個位置的局部損傷。
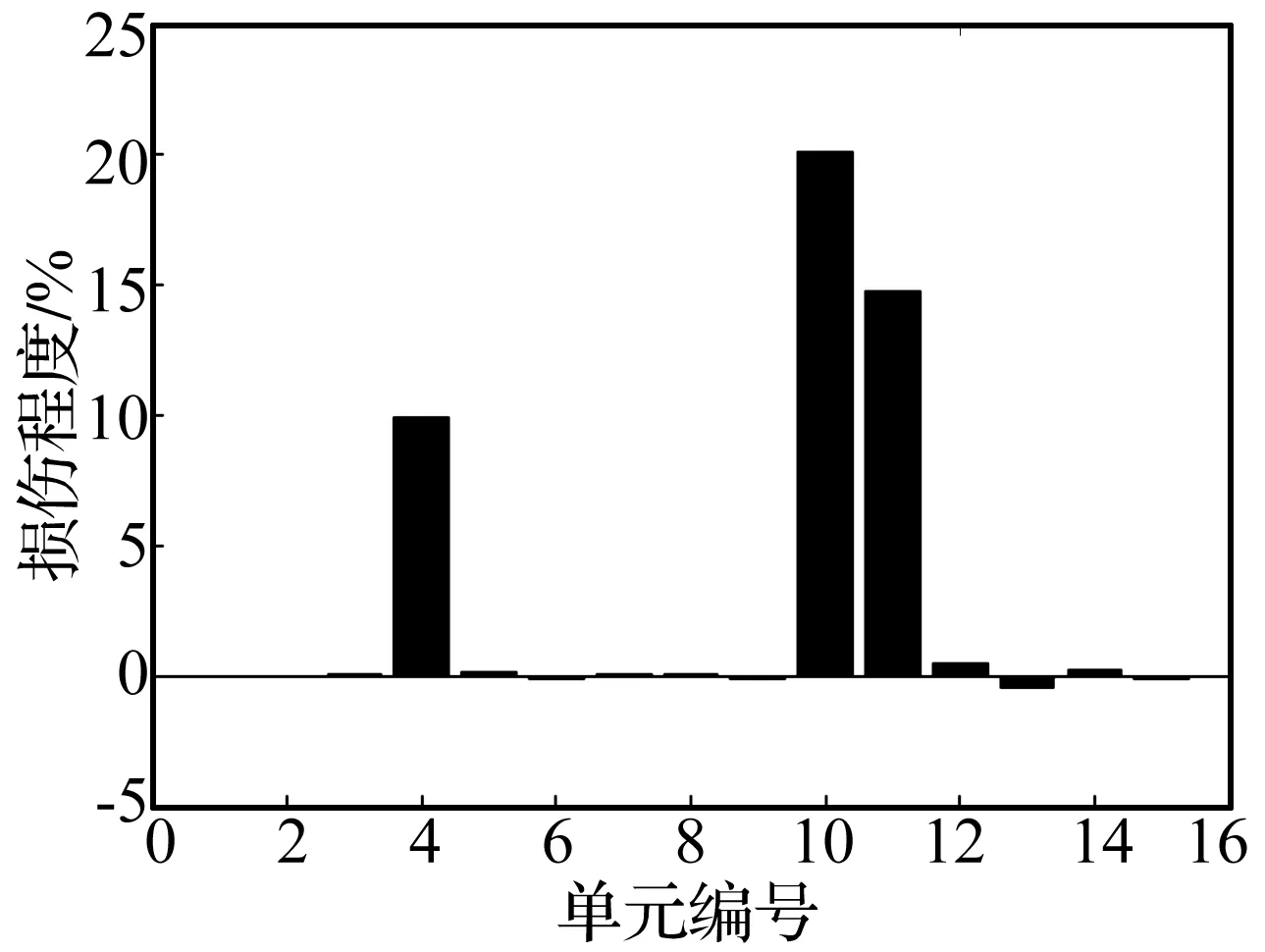
圖3 多損傷檢測
4 結 論
本文研究基于功率譜靈敏度分析的損傷識別算法,數值算例結果表明,僅用較少傳感器響應功率譜,在激勵譜已知時能準確檢測結構單一、多個位置局部損傷。表明本文所提方法具有一定應用前景。對未討論的噪音及由時域信號所得結構響應功率譜過程誤差對識別結果影響,有待深入研究。
[1] Messina A, Williams E J, Contursi T. Structural damage detection by a sensitivity and statistical-based method[J]. Journal of Sound and Vibration, 1998, 216(5):791-808.
[2] Zhao J, DeWolf J T. Sensitivity study for vibrational parameters used in damage detection[J]. Journal of Structural Engineering, ASCE, 1999, 125(4):410-416.
[3] 劉濟科,李雪艷.基于靈敏度分析的機械系統損傷識別方法[J].機械科學與技術,2002,21(3):456-459.
LIU Ji-ke, LI Xue-yan. A sensitivity based method for damage identification of mechanical structures[J]. Mechanical Science and Technology,2002,21(3):456-459.
[4] Thyagarajan S K, Schulz M J, Pai P F. Detecting structural damage using frequency response functions[J]. Journal of Sound and Vibration, 1998, 210(1):162-170.
[5] 楊秋偉. 結構損傷識別的附加質量方法[J]. 工程力學, 2009, 26(5):159-163.
YANG Qiu-wei. Structural damage identification by adding given masses[J]. Engineering Mechanics, 2009, 26(5):159-163.
[6] 王真, 程遠勝. 基于時間序列模型自回歸系數靈敏度分析的結構損傷識別方法[J]. 工程力學, 2008, 25(10): 38-43.
WANG Zhen, CHENG Yuan-sheng. Structural damage identification based on sensitivity analysis of autoregressive coefficients of time series models[J]. Engineering Mechanics, 2008, 25(10): 38-43.
[7] Lu Z R, Law S S. Identification of system parameters and input force from output only [J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2099-2111.
[8] Zhang K, Law S S, Duan Z D. Condition assessment of structures under unknown support excitation[J]. Earthquake Engineering and Engineering,2009,8(1):103-114.
[9] 林家浩, 張亞輝. 隨機振動的虛擬激勵法[M]. 北京: 科學出版社, 2004.
[10] 徐文濤, 張亞輝, 林家浩. 基于虛擬激勵法的車輛振動靈敏度分析及優化[J].機械強度,2010,32 (3):347-352.
XU Wen-tao. ZHANG Ya-hui. LIN Jia-hao. PEM based sensitivity analysis for vehicle ride comfort and optimization[J]. Journal of Mechanical Strength, 2010,32 (3): 347-352.
[11] Bathe K J. Finite element procedures in engineering analysis [M]. Prentice Hall,New Jersey, 1982.
[12] Tikhonov A M. On the solution of ill-posed problems and the method of regularization[J]. Soviet Mathematics, 1963, 4:1035-1038.
[13] Hansen P C. Analysis of discrete ill-posed problems by means of the L-curve[J]. SIAM Review,1992,34(4):561-580.

