考慮幾何非線性效應的大展弦比機翼氣動彈性分析

楊智春，張 惠，谷迎松，宋 淼

(西北工業大學 航空學院結構動力學與控制研究所，西安 710072)

無人機機翼通常采用大展弦比構型，具有重量輕、柔性大特點；但其在氣動載荷作用下會產生較大結構變形，致基于結構小變形假設的常規線性氣動彈性分析方法不再適用。大展弦比機翼氣動彈性分析須考慮結構大變形導致的幾何非線性效應。Kim等[1]通過采用跨音速小擾動理論與大變形梁理論耦合分析大展弦比機翼幾何非線性顫振特性，較好預測顫振邊界。Dowell[2]對陣風響應下大展弦比機翼氣動彈性特性進行理論分析與風洞實驗研究，認為陣風載荷較小時幾何非線性對垂向、扭轉響應影響較小。Patil等[3]通過研究大展弦比機翼靜/動氣動彈性特性，認為大變形幾何非線性對大展弦比機翼靜/動氣動彈性特性有重要影響。Choi等[4]采用MSC.Nastran與CFD軟件耦合分析翼型(不同根梢比及后掠角)對機翼氣動彈性特性影響，認為弦長不變具有錐形外截面翼型的升力系數更高、氣動彈性特性更優。安效民等[5]用近似能量守恒幾何大變形下殼體結構非線性動態響應算法結合求解雷諾平均N-S方程的CFD求解器發展的高效耦合格式，模擬流場非線性及結構非線性氣動彈性響應。謝長川等[6]用線性化方法計算大展弦比機翼飛機在平飛設計載荷及陣風載荷作用下非線性靜變形，分析結構幾何非線性對大展弦比機翼固有振動特性及顫振特性影響。劉湘寧等[7]研究結構非線性對復合材料大展弦比機翼顫振特性影響結果表明，用非線性模型計算所得顫振速度小于線性模型所得顫振速度。

由以上研究知，大展弦比機翼幾何非線性顫振由機翼在定常氣動載荷作用下大變形所致。求解機翼非線性顫振特性前須先求解機翼在定常氣動載荷作用下的靜變形。為此，本文提出考慮靜氣動彈性效應及大變形幾何非線性的大展弦比機翼氣動彈性分析方法。即在給定飛行狀態及機翼初始構型下求解機翼結構的定常氣動載荷；采用考慮靜氣動彈性效應迭代方法求解大展弦比機翼結構非線性靜變形，在收斂的大變形構型下獲得考慮機翼結構幾何非線性效應的剛度矩陣；再進行機翼的準線性模態及顫振特性分析。本文用MATALAB軟件平臺對MSC.Nastran軟件二次開發，實現計算流程，并對大展弦比機翼模型[3]進行分析，計算該機翼非線性氣動彈性特性，所得結果與文獻[3]一致，驗證本文所建分析方法及平臺的正確性。

1 大展弦比機翼非線性氣動彈性特性分析

1.1 考慮大變形幾何非線性結構剛度矩陣

結構幾何非線性對大展弦比機翼氣動彈性特性影響主要體現于結構剛度特性隨載荷工況改變及機翼非線性變形會影響機翼的氣動力分布。機翼幾何非線性大變形中結構應變仍為小量,因此用有限元法對大展弦比機翼結構進行幾何非線性大變形分析時材料應力應變關系仍為線性，其平衡方程由變形后幾何關系描述，但結構剛度特性需用切線剛度矩陣描述[8],即

K=K0+Kσ+KL

(1)

式中：K0為小位移(彈性)剛度矩陣，與單元節點位移無關；KL為大位移剛度矩陣，與單元節點位移有關；Kσ為初應力剛度矩陣。

1.2 機翼結構準線性模態分析

機翼在大變形平衡位置附近作微幅振動時可認為振動仍為線性，其振動方程為

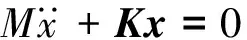
(2)

式中：x為機翼結構偏離大變形平衡位置位移列陣；M為機翼結構質量矩陣；K為機翼結構在大變形平衡位置處切線剛度矩陣。

設機翼微振動為簡諧振動：

x=Xeiωt

(3)

代入式(1)得：

KX=ω2MX

(4)

式中：ω2為特征值；X為特征向量。分別對應機翼在大變形平衡位置處的準線性模態頻率及模態振型。

1.3 機翼氣動載荷

對大展弦比機翼分析時可采用亞音速偶極子格網法計算其氣動載荷，在各升力面網格1/4弦線處布置一馬蹄渦，用加速度勢偶極子模擬機翼氣動力非定常項。每一氣動網格單元的非定常壓差為

(5)

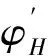
1.4 非線性靜氣動彈性變形分析

靜氣動彈性變形分析基本方程[9]為

(6)

分析單獨機翼靜氣動彈性變形時用根部固支邊界條件約束機翼結構剛體自由度。氣動面定常氣動力為

(7)

本文通過Matlab編程由MSC.Nastran軟件的靜氣動彈性計算結果中提取。

進行機翼非線性靜變形分析時需將空氣動力通過樣條插值矩陣變換為作用在結構網格節點等效力完成。樣條矩陣Gkg為由結構網格點位移ug到氣動力網格點位移uk的變換，可表示為

uk=Gkgug

(8)

據虛功原理，空氣動力Fk及作用在結構網格節點的等效力Fg在相應虛位移上做功相等，得：

(9)

式中：δuk，δug為虛位移。

將式(8)代入式(9)得：

(10)

據虛位移任意性，得：

(11)

1.5 顫振特性分析

在機翼結構大變形平衡位置處準模態分析基礎上可得機翼在模態坐標系下的顫振運動方程為

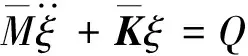
(12)

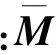
方程(12)的解可表示為

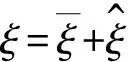
(13)

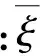
(14)

在顫振臨界點，機翼小擾動振動為簡諧運動,即

(15)

由式(14)可得顫振行列式為

(16)

采用p-k法求解廣義特征值可得考慮機翼大變形幾何非線性的顫振臨界速度及顫振頻率。

2 考慮結構幾何非線性氣動彈性特性分析

為使分析過程自動化便于工程應用，本文在Matlab軟件平臺上對MSC.Nastran軟件進行二次開發，實現大展弦比機翼大變形幾何非線性氣動彈性分析方法計算流程。分析過程有三步，即考慮大變形幾何非線性氣動彈性靜變形分析、大變形靜平衡位置處準模態分析及大變形靜平衡位置處顫振分析。分析流程見圖1。計算過程為：① 在MSC.Patran軟件中建立大展弦比機翼結構模型及氣動力模型；設定機翼初始飛行狀態(來流速度、飛行高度、馬赫數等)，調用MSC.Nastran軟件進行靜氣動彈性變形分析與氣動載荷分析。② 用DAMP語言編程，將氣動面的定常氣動力轉化為每個結構節點的氣動載荷，將氣動載荷與慣性載荷輸出為各節點的外力載荷。③ 據所得節點外力載荷，用MSC.Nastran軟件對結構進行大變形幾何非線性分析，獲得節點靜變形。④ 判斷變形是否收斂，若此次非線性計算所得節點靜變形與前次計算結果相差達到預設精度，迭代收斂；否則，對變形機翼更新氣動面計算網格，轉到步驟①繼續迭代。⑤ 變形收斂后提取非線性靜平衡位置處切線剛度矩陣、質量矩陣，對機翼進行靜平衡位置處準模態分析。⑥據圖1顫振分析模塊計算獲得考慮大變形幾何非線性的機翼顫振速度。若顫振速度與靜氣動彈性計算時來流速度不匹配，則更新靜氣動彈性分析中速度進行迭代計算，顫振速度與靜氣動彈性變形計算時速度一致時，該速度即為給定初速度攻角的匹配顫振速度。

圖1 考慮幾何非線性效應的機翼氣動彈性特性分析流程

3 考慮結構幾何非線性的氣動彈性特性分析算例

3.1 機翼的線性顫振分析

為對比說明大變形幾何非線性對大展弦比機翼臨界顫振特性影響、驗證氣動網格的準確性，對大展弦比機翼模型[3]的線性模態特性及顫振特性進行研究。模型數據見表1。機翼有限元模型用20個梁單元，機翼質量用分布質量。不考慮機翼大變形幾何非線性因素，直接用線性振動分析所得機翼振動頻率與文獻[3]結果比較見表2，兩者吻合較好。

表1 機翼模型數據[3]

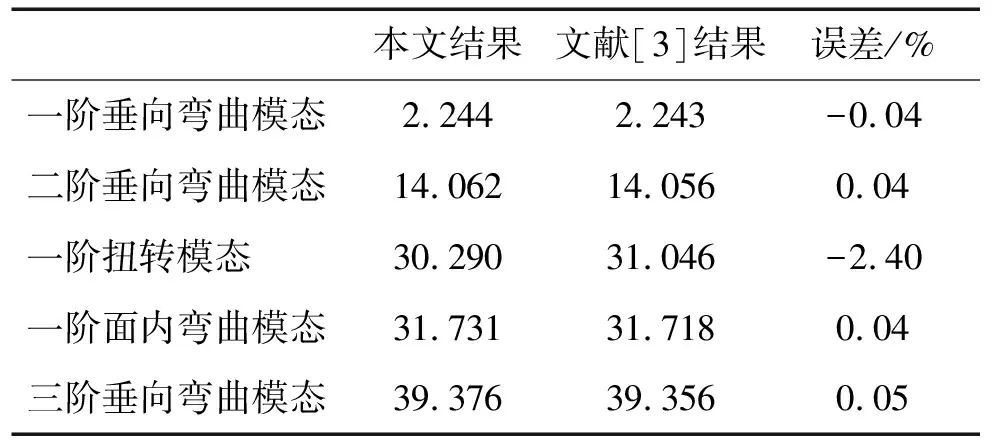
表2 線性振動分析模態頻率(rad/s)

機翼線性顫振特性見表3，與文獻[3]結果比較看出，顫振頻率基本相同，顫振速度相對誤差5.7%。分析認為該誤差由本文計算非定常氣動力時用亞音速偶極子網格法而文獻[3]用簡化片條氣動力理論所致。

表3 線性顫振特性比較

3.2 機翼氣動彈性特性分析

利用文獻[3]算例模型,考慮大變形幾何非線性因素,采用本文方法進行分析。機翼顫振速度、顫振頻率隨攻角變化曲線見圖2(a)、(b)。文獻[3]認為根部攻角在0.61°附近時顫振速度有一個跳躍，跳躍點后機翼顫振速度隨攻角變大而平穩降低。本文所得翼梢變形隨攻角變化規律見圖2(c)。分析結果與文獻[3]變化趨勢一致。數值上所存差異原因同前分析。

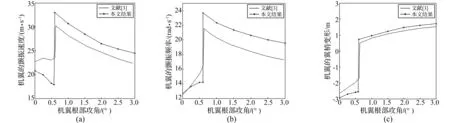
圖2 機翼根部攻角對非線性氣動彈性特性影響

由算例結果表明，采用本文的基于MSC.Nastran軟件平臺、考慮結構大變形幾何非線性效應大展弦比機翼氣動彈性特性分析方法求解大展弦比柔性機翼的幾何非線性顫振可行，亦為工程提供簡便有效手段。

4 結 論

本文通過建立考慮大變形幾何非線性效應的大展弦比機翼氣動彈性特性分析方法，研究大變形幾何非線性效應對機翼顫振特性影響，結論如下：

(1) 顫振特性隨根部攻角穩定變化后，大展弦比柔性機翼大變形所致幾何非線性效應會使機翼顫振臨界速度顯著降低；

(2) 翼梢變形隨攻角增大而增大，機翼扭轉頻率隨翼梢變形增大而降低，機翼幾何非線性顫振臨界速度隨攻角增大而降低。

[1] Kim K S, Lee I, Lee H K. Efficient numerical aeroelastic analysis of a high-aspect-ratio wing considering geometric nonlinearity[J]. Journal of Aircraft, 2010, 47(1):338-342.

[2] Dowell E H. Gust response for flexibly suspended high-aspect ratio wings [J]. AIAA, 2010, 48(10):2430-2444.

[3] Patil M J, Hodges D H. Nonlinear aeroelasticity and flight dynamics of high-altitude long-endurance aircraft [J]. Journal of Aircraft, 2001,38(1):88-94.

[4] Choi S, Park K,Kim J,et al. Aeroelastic characteristics of high-aspect-ratio wing according to wing shape[J]. AIAA, 2013,143:1-8.

[5] 安效民,徐敏. 一種幾何大變形下的非線性氣動彈性求解方法[J].力學學報,2011,43(1):98-104.

AN Xiao-min, XU Min. An improved geometrical nonlinear algorithm and its application for nonlinear aeroelasticity [J].Chinese Journal of Theoretical and Applied Mechanics, 2011,43(1):98-104.

[6] 謝長川,楊超. 大展弦比飛機幾何非線性氣動彈性穩定性的線性化方法[J]. 中國科學:技術科學,2011,41(3):385-393.

XIE Chang-chuan, YANG Chao. A linearization method to analyze geometrical nonlinear aeroelastic stability of the high-aspect-ratio aircraft[J]. Science China,2011,41(3):385-393.

[7] 劉湘寧, 向錦武.大展弦比復合材料機翼的非線性顫振分析[J]. 航空學報, 2006, 27(2):214-218.

LIU Xiang-ning, XIANG Jin-wu. Study of nonlinear flutter of the high-aspect-ratio composite wing[J].Chinese Journal of Aeronautics, 2006, 27(2):214-218.

[8] 呂和祥,蔣和洋. 非線性有限元[M]. 大連：化學工業出版社, 1991.

[9] Rodden W P, Johnson E H. MSC/NASTRAN version 68 aeroelastic analysis users guide[M]. New York: The MacNeal-Schwendler Corporation, 1994.

[10] Dowell E H,Traybar J,Hodges D H. An experimental-theoretical correlation study of non-linear bending and torsion deformations of a cantilever beam[J].Journal of Sound and Vibration, 1977, 50(4):533-544.