柔性梁分布式外部載荷識別方法

劉 濤，吳 煒，史濟濤，蔡國平

(1.上海交通大學 工程力學系，海洋工程國家重點實驗室，上海 200240；2.中國空空導彈研究院，河南 洛陽 471009)

動態載荷確定一直為結構動力學研究重要及難點，而動載荷準確識別為確保結構設計安全、可靠的基本保障；因此，開展動載荷識別技術研究具有重要理論意義及工程應用價值。確定結構動載荷方法有直接測量方法、間接識別方法兩種。前者可由直接測量載荷本身或與載荷有關參數確定載荷大小；但對大多數工程結構，所受外部動態載荷較難直接測量獲得，如火箭飛行中所受推力、導彈飛行中所受外部風載荷等需采用間接方法對外部載荷進行辨識，即載荷識別技術。動態載荷識別為結構動力學中第二類逆問題，為在已知結構模型及系統輸出情況下對載荷進行反演。

動載荷識別技術研究源于航空業。Bartlett等[1]為確定直升機槳轂中心主要諧波頻率下動載荷幅值及相位采用頻域法進行動態載荷識別研究。動載荷識別有頻域法、時域法兩種[2-4]。頻域法識別原理簡單、直觀，在頻域內建立系統逆向頻率響應函數模型，通過系統輸出對動態輸入進行識別。時域法由Ory等[5]考慮運載火箭飛行載荷時首次提出。時域識別基本思想即利用結構模態參數建立系統在時域內的逆向模型，通過系統動態響應輸出識別動態載荷。時域法便于工程應用，使動載荷在線識別成為可能。除頻域法、時域法外，隨信號處理分析手段、模式識別方法等各種交叉學科發展，如小波分析、基于系統辨識理論的逆系統法、神經網絡等逐漸成為動態載荷識別的新工具[2-4]。

本文以柔性梁為對象，采用擾動力觀測器與變結構控制相結合方法，給出可分離變量的分布式外部載荷識別技術，并通過數值仿真驗證該方法的有效性。對曾采用本文識別技術并以柔性懸臂梁為對象對集中力形式外部載荷進行的識別，效果良好[6]。

1 動力學方程

本文考慮等截面柔性梁橫向彎曲振動，見圖1。設梁受分布式外部載荷作用，并有r個集中力形式作動器用于梁的振動控制。梁振動方程可表示為

(1)

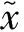
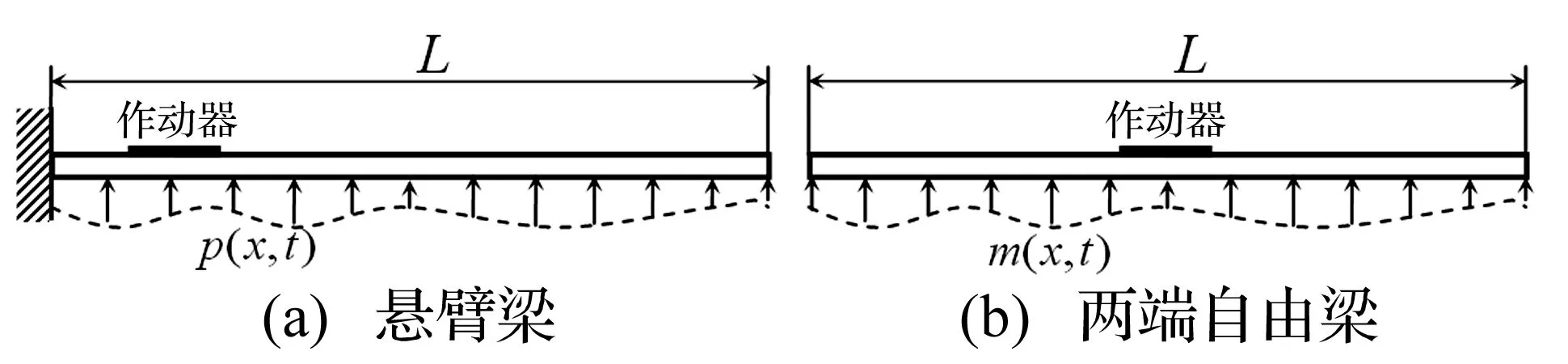
圖1 柔性梁結構模型

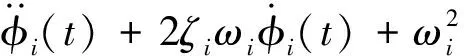
(2)

式中：ωi為梁第i階模態振動固有頻率；nci(t)，ndi(t)分別為第i階模態控制力、激振力，分別表示為

(3)

式中：L為梁長。

僅考慮分布式外力p(x,t)可拆分為p(x,t)=h(x)f(t)，則第i階模態激振力ndi(t)可描述為

(4)

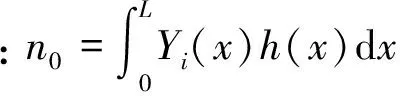
僅考慮分布式外力矩m(x,t)可拆分為m(x,t)=h′(x)g(t)，且m(0,t)=0，m(L,t)=0，則第i階模態激振力ndi(t)可描述為

(5)

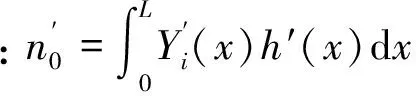
(6)

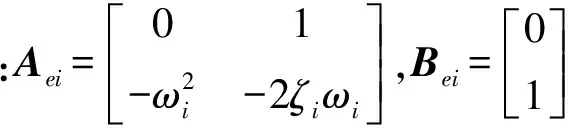
將式(6)離散化，有：

Zi(k+1)=AiZi(k)+Binci(k)+Bindi(k)

(7)

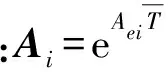
2 控制設計與擾動力觀測器

本文采用離散變結構控制與擾動力觀測器相結合的載荷識別方法。柔性梁振動主動控制采用獨立模態空間方法，其中控制律設計用離散變結構控制方法，包括切換面確定及控制律設計兩部分。

2.1 切換面設計

獨立模態空間控制方法要求用r個作動器分別對梁前r階模態進行主動控制，需確定r個切換面，每個模態控制力皆有自己獨立的切換面。切換面設計時，可不考慮外部激勵項，此項在控制律設計中予以考慮[7]。式(7)可寫為

Zi(k+1)=AiZi(k)+Binci(k)，(i=1～r)

(8)

設切換函數具有線性形式[8-9]為

si(k)=CiZi(k)，(i=1～r)

(9)

式中：系數矩陣Ci∈R1×2為待確定的切換函數系數向量。

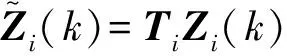
(10)

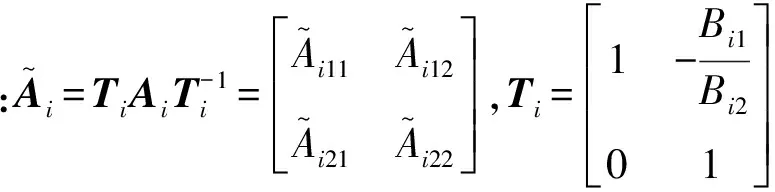
式(9)切換函數可改寫為

(11)

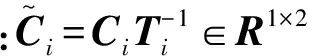
展開式(10)，有：

(12)

定義控制模態性能指標為

(13)

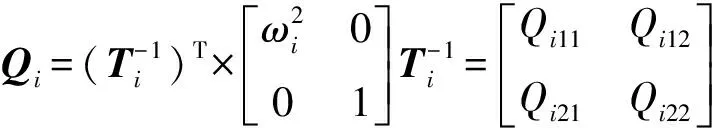
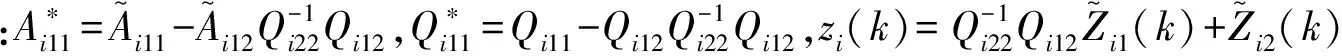
(14)

(15)

式(14)、(15)為二次型最優控制問題。據最優控制理論得：

(16)

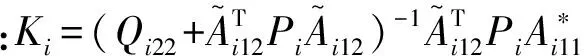
(17)

由此，系統滑移模態為穩定的，可改寫為

(18)

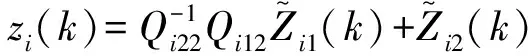
(19)

(20)

式中：C0為常系數，可通過調整C0值使Ci第二個分量為1。由此完成切換面設計。

2.2 控制律及擾動力觀測器

本文采用離散變結構控制器與擾動力觀測器[8-9]。為減小符號函數引起的抖振現象，將原式中符號函數替換為飽和函數：

qisi(k-1)+κisat[si(k-1)/φi]}

(21)

qisi(k)-κisat[si(k)/φi]}

(22)

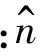
(23)

式中：ndi(k)為k時刻外部擾動力實際加載值。

飽和函數sat定義為

(24)

在滿足以上選取條件范圍內，合理選擇參數可減小抖振，使控制及辨識效果更佳。變結構控制方法能取得較好控制效果在于控制律表達式中含外部激勵項，故提出如式(21)預估外部載荷的觀測器方法。

3 數值仿真

進行數值仿真驗證本文所給方法的有效性。分別考慮懸臂梁及自由-自由梁兩種模型(圖1)，梁為鋁合金材質，尺寸1 000 ×35×1.5 mm3，密度ρ=2 766 kg/m3，彈性模量E=69 GPa。考慮用壓電片為作動器，用于梁的振動控制。為取得較好控制效果，壓電片置于梁應變較大處。因此，設懸臂梁根部附近粘貼一片壓電作動器(圖1(a))，壓電作動器尺寸60×15×0.5 mm3，作動器左端距梁固定端xl=70 mm，壓電常數d31=17.5×10-9m/V，彈性模量Et=63 GPa。對自由-自由梁，將作動器壓電片置于梁中點位置(圖1(b))。數值仿真中截取梁前10階模態響應為梁的真實響應，各階模態阻尼比取值均為ζi=0.05；式(23)中各參數取值為q1=0.5，κ1=1.6×10-3，g1=0.98，φ1=1.1×10-3。

3.1 懸臂梁仿真

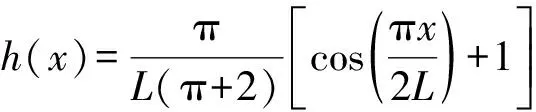
3.2 自由-自由梁仿真

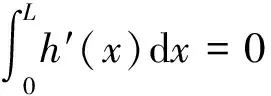
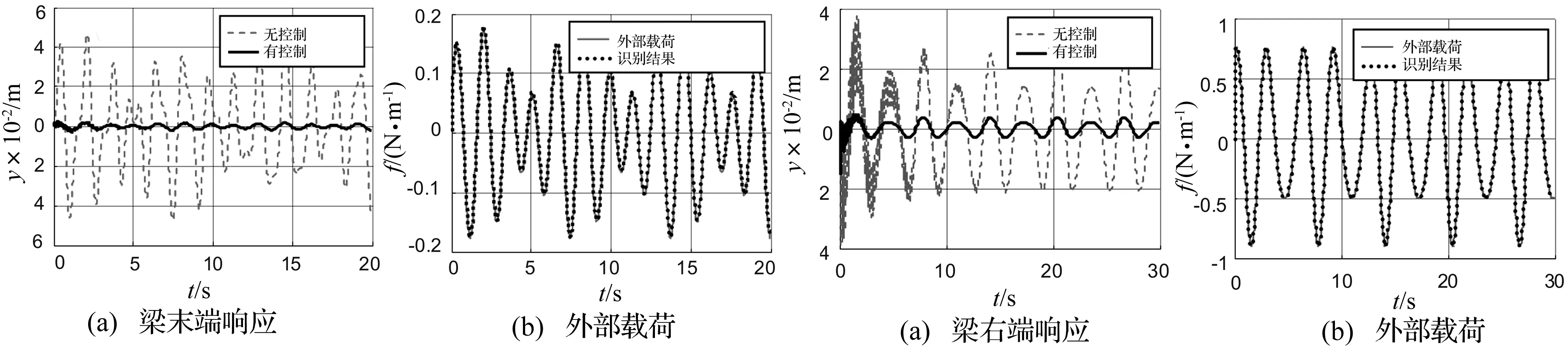
圖2 懸臂梁末端響應與載荷辨識結果

4 結 論

本文以柔性梁為研究對象，給出基于變結構控制方法設計的分布式外部載荷識別方法。其擾動力觀測器可用于實時觀測外部載荷變化情況，并將觀測結果用于控制律計算。仿真結果表明，變結構控制律能有效用于柔性梁彈性振動，擾動力觀測器能有效識別外部載荷。

[1] Bartlett F D, Flannelly W D. Model verification of force determination for measuring vibration loads[J]. Journal of the American Helicopter Society, 1979, 24(2): 10-18.

[2] 耿苗. 連續分布動載荷識別的頻域方法[D]. 南京:南京航空航天大學, 2006.

[3] 張勇成. 二維分布動載荷時域識別技術[D]. 南京:南京航空航天大學, 2007.

[4] 秦遠田. 動載荷識別應用技術研究[D]. 南京:南京航空航天大學, 2007.

[5] Ory H, Glaser H, Holzdeppe D. The reconstruction of forcing function based on measured structural responses[C]. Proceeding of 2nd International Symposium on Aeroelasticity and Structural Dynamics, Aachen, FRG, 1985.

[6] 蔡明哲,李超,洪文超,等. 柔性結構的載荷識別[J]. 噪聲與振動控制,2013,33(1):64-67.

CAI Ming-zhe, LI Chao, HONG Wen-chao, et al. Load identification of flexible structures[J]. Noise and Vibration Control, 2013, 33(1): 64-67.

[7] Yang J N, Wu J C, Agrawal A K. Sliding mode control for nonlinear and hysteretic structures[J]. Journal of Engineering Mechanics, ASCE, 1995, 121(12):1330-1339.

[8] Wang D A, Huang Y M. Application of discrete-time variable structure control in the vibration reduction of a flexible structure [J]. Journal of Sound and Vibration, 2003, 261(3):483-501.

[9] Gao Wei-bing. Discrete-time variable structure control systems[J]. IEEE Transactions on Industrial Electronics, 1995, 42(2): 117-122.