一種基于可預測偏最小二乘法的故障檢測方法

王 丹 楊煜普 屈衛東

(上海交通大學電子信息與電氣工程學院自動化系，上海 200240)

近年來，隨著現代化工及冶金等工業過程日益大規模化和復雜化，工業過程的安全問題越來越受到人們的關注。基于多元統計分析的故障檢測與診斷方法也成為近年來故障檢測與診斷領域的研究熱點，并在工業過程中成功應用[1～3]。偏最小二乘(PLS)技術能夠根據正常工況的生產數據，準確捕捉質量變量與過程變量之間的關系，對生產工況進行有效監測，且PLS統計檢測技術不依賴于過程機理模型，訓練時不需要故障樣本，能夠彌補其他統計方法(例如PCA)無法考慮過程變量對質量變量影響的不足，因此近年來在化工過程的質量控制及在線檢測等方面得到了廣泛研究和應用[4～6]。但是PLS方法無法反映過程的動態時序特性，這在一定程度上影響了它的故障檢測準確率。可預測元分析[7](Forecastable Component Analysis，ForeCA)作為一種新的統計信號處理方法克服了這個不足。可預測元分析是一種全新的用于多變量時序相關信號的特征提取方法，它能從已有的數據中捕捉到系統的動態特性，并以此來預測系統運行變化的趨勢，因此所提取的特征能從本質上描述工業過程。

筆者將可預測元分析方法與偏最小二乘法回歸方法相結合并用于故障檢測，通過將樣本映射到可預測子空間，使用最小二乘回歸，進一步提高了模型的預測性能，同時構造CUSUM和SPE統計量對系統進行監控，這樣能夠較好地檢測均值偏差在兩倍標準差以下的故障。該方法克服了傳統偏最小二乘法無法反映過程時序特性的不足，能夠預測系統運行變化的趨勢，反映出系統的動態特性，因此能夠提升故障檢測的準確率。

1 基本算法①

1.1 可預測元分析

可預測元分析的基本思想是假設矩陣X∈Rn×m，其中n為樣本個數，m為變量個數，通過線性變換WT∈Rk×n，可得：

S=WTX

(1)

其中W為由可預測元列向量組成的可預測元矩陣，S為得分矩陣，ForeCA需要解決的問題即由觀測矩陣X估計S和W。

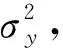
γy(k)=E(yt-μy)(yt-k-μy)T,k∈R

(2)

其中k為時延。

定義單變量平穩過程的譜密度為對其自協方差函數的傅里葉變換，得：

(3)

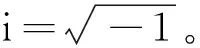
(4)

由文獻[7]可知，一個平穩過程的熵越大越難被預測，且白噪聲無法被預測，可得：

Hs,a(yt)≤Hs,a(白噪聲)

(5)

因此可定義平穩過程的可預測度為：

(6)

對于多變量二階平穩過程Xt，考慮線性變換yt=wTXt，其中w(w∈Rn)是式(1)中W的列向量，即可預測元，此時yt可以看成是一個單變量的二階平穩過程。文獻[7]給出了ForeCA的最優化問題：

(7)

s.t.wTΣXw=1

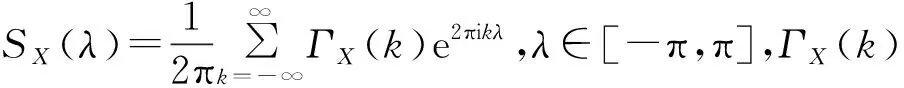
對式(7)進行求解，首先使用加權交疊平均譜估計法對隨機過程進行譜密度估計[8]，再使用EM-Like算法求取可預測元[7]。文獻[7]給出了此算法的詳細步驟，通過此算法可以得出一組按照可預測度由高到低順序排列的可預測元，即可得到式(1)中的可預測元矩陣wT。

1.2 偏最小二乘法

給定輸入矩陣X∈Rn×N包含n個樣本，每個樣本N個過程變量，輸出矩陣Y∈Rn×M包含n個樣本，每個樣本M個質量變量。PLS通過隱變量對兩個數據塊的關系進行建模，它將n×N零均值矩陣X和n×M零均值矩陣Y分解為：

(8)

(9)

式中Ek、Fk——擬合誤差矩陣；

P——X的負載矩陣；

Q——Y的負載矩陣；

T——得分矩陣，T=[t1,…,tk]；

在PLS模型中，負載向量和得分向量通過最大化解釋各自的信息，同時也使X與Y的相關程度最大來求得。最常見的計算PLS模型的算法是Nipals算法，Y的預測回歸方程為：

(10)

其中，BPLS是PLS回歸系數矩陣，權重矩陣M是由Nipals算法定義的，T=XM。

在復雜的多變量系統中，PLS算法將自變量X和因變量Y看成是具有線性關系的數據矩陣。沒有逐個對變量判斷其留取與舍棄，而是利用信息分解的思路將顯變量系統中的信息重新組合，綜合篩選，提取出既能最大程度解釋自變量信息，又能最大程度反映自變量與因變量間線性關系的互相正交的綜合變量(隱變量)。PLS用獨立的隱變量進行建模、預測，使得該方法可以廣泛應用于數據不完整、變量間存在多重相關性的場合。

2 基于ForePLS的故障檢測模型

2.1 CUSUM統計量

工業過程中存在很多慢漂移的故障，為了檢測這種微小的變化，筆者用CUSUM統計量對其進行檢測。基于CUSUM統計量的表格累加法為了檢測樣本均值向上和向下漂移，定義了兩個統計量，即：

SH(i)=max[0,xi-(μ0+K)+SH(i-1)],SH(0)=0

(11)

SL(i)=max[0,(μ0-K)-xi+SL(i-1)],SL(0)=0

(12)

(13)

其中μ0是樣本實際的均值，xj為第j個樣本值，筆者用訓練樣本均值代替。K為參考值，一般取0.5Δ，Δ為期望檢測出的偏差，取值在[0.5σ,2.0σ]內。其控制限為5倍的標準差[9]。

2.2 SPE統計量

首先選取一段正常工況下的觀測數據X(X∈Rn×N)，其中n為變量個數，N為采樣點數，對其運用ForeCA算法，得可預測元矩陣：

WT=[w1,w2,…,wn]T∈RN×N

(14)

(15)

過程殘差可表示為：

(16)

(17)

SPE統計量的控制限用核密度估計確定，具體參見文獻[11]。

2.3 基于ForePLS的故障檢測步驟

基于ForePLS的故障檢測分為兩個階段——離線訓練階段和在線檢測階段。

離線訓練階段。首先采集正常工況下的訓練數據X，對其進行預處理后，使用ForeCA算法提取出可預測主元矩陣W，然后在可預測子空間進行PLS回歸，再計算訓練數據在可預測子空間的CUSUM統計量和SPE統計量，最后計算兩個統計量的控制限——H和SPEα。

在線檢測階段。首先根據實時采集的未知狀態的數據集，將此可預測模型運用于在線數據，分別計算每個樣本數據的CUSUM和SPE統計量，最后比較兩個統計量與其對應控制限的大小，通過比較確定系統是否發生故障。如果檢驗結果在控制限以內，則說明目前系統工作在可預測模型所預測的變化范圍之內，即系統工作正常；反之，則說明目前系統的工作狀態已經偏離可預測模型所預測的變化范圍，判斷系統已經出現了故障。

3 TE實驗平臺故障分析

TE實驗平臺是Downs和Vogel根據Eastman化學公司的世界工藝流程做了少許修改于1993年提出的[12]，其中包含21個預設故障。TE過程由連續攪拌式反應釜、分凝器、氣液分離塔、汽提塔、再沸器及離心式壓縮機等多個操作單元組成，其流程如圖1所示。

圖1 TE流程

TE過程共有A、C、D、E 4種氣體進料，G和H兩種反應產物，F一種副產品。系統中存在的化學反應如下：

以上各式中，g代表氣體，liq代表液體。所有的反應都是不可逆放熱反應，反應速度取決于溫度和反應物的氣相濃度。

TE模型用于訓練的樣本數據為500個52維向量，用于測試的樣本數據為960個52維向量，其中故障從第161個樣本點開始引入。筆者選擇過程中的G和H(即MEAS35和MEAS36)作為ForePLS模型的質量變量Y；選取22個過程變量MEAS1～22和11個操作變量MV1～11作為X。采用ForePLS模型對TE過程的反應產物G的含量的預測結果如圖2所示，可以看出ForePLS有很好的預測能力。

圖2 故障10發生時產品中組分G的含量曲線

下面以隨機變化故障中典型的故障IDV(10)為例加以分析。故障IDV(10)發生時，供料C的溫度產生了隨機變化。為了驗證ForePLS的有效性，將其與PCA和PLS兩種方法進行對比。實驗中，ForePLS的隱變量個數為6，PCA的主元個數為15，PLS的隱變量個數為9，期望檢測到的均值偏離為0.5倍的標準差。圖3顯示了PCA、PLS和ForePLS 3種方法對故障IDV(10)的檢測效果。可以看出，PCA的T2統計量和SPE統計量的準確率分別為45.6%和53.9%；PLS的兩個統計量的檢測準確度都較低，分別為18.8%和27.8%；ForePLS的CUSUM和SPE統計量的準確率為96.5%和52.9%。由此說明，筆者所提出的基于ForePLS的故障檢測方法檢測隨機變化的故障準確率比PCA和PLS方法更好。

圖3 IDV(10)發生時PCA、PLS和ForePLS方法的故障檢測性能比較

4 結束語

介紹了一種基于可預測元分析和最小二乘回歸法相結合的故障檢測方法。該方法克服了傳統最小二乘法無法反映過程時序特性的不足，能夠有效預測系統運行變化的趨勢，反映出系統的動態特性。通過檢測可預測空間上的CUSUM統計量和SPE統計量，以達到檢測慢漂移等微小故障和隨機變化故障的目的。在TE模型上的仿真表明：該方法比傳統的PCA、PLS方法檢測精度更高，效果更好。