談談錯例資源在數學教學中的作用

張啟淼

（福建省尤溪縣八字橋中學，福建 尤溪 365100）

談談錯例資源在數學教學中的作用

張啟淼

（福建省尤溪縣八字橋中學，福建 尤溪 365100）

數學練習中學生出現錯誤是美麗的，是他們樸實思想最真實的流露。用資源的眼光看待學生學習中的錯誤，錯誤其實是學生在學習過程中創造出的一種寶貴的教學資源，是一種來源于學習活動本身，直接反映學生學習情況的生成性教學資源。結合我多年教學的實踐，談談個人的幾種看法。

教學資源；錯例；求知欲

在平時的教學中，我們常常會遇到這樣的現象：重要的知識點講過多次之后學生還是會出錯，大有“野火燒不盡，春風吹又生”之勢。而且學生在課堂上、作業中出現的錯誤經常是類同的，有些錯誤是一犯再犯，甚至有的學生一道題目需要訂正好幾次才能訂正好。但長期以來，對待學生學習上的錯誤，我們缺乏一種“主動應對”的理念和策略，導致在教學實踐中經常可以看到有相當一部分學生對于相同的錯誤屢犯不止，學生學習時間的無效流失，影響著教學質量。

俗話說：“失敗是成功之母”，錯誤是正確的先導，是通向成功的階梯，是創新火花的表現，我們要懂得“變廢為寶”。教師要善待學生的錯誤，并善于挖掘學生錯誤思維中的合理因素，學會欣賞錯誤思維中的創新因素，將錯誤轉化為寶貴的教學資源，讓錯誤發揮出它最大的價值和功能。下面，我根據多年的教學實踐，從以下幾個方面談談我個人的看法。

一、錯例是激發學生求知欲的有效措施

錯例分析具有正例示范所不可替代的作用，兩者相輔相成，構成完整的解題教學。教師做好典型錯例分析，尋找跟進對策是幫助學生學會學習的方法之一。教師通過錯題分析或者通過師生的共同分析，找到錯題的癥結所在，采取相應的方法輔導、改進后，再讓學生進行相應的練習，學生的正確率會有較大的提高，面對自己的學習效果，加上教師的激勵性評價，學生的信心大大增強，是激發學生求知欲的有效措施。

例如，在“分式的運算”課中讓學生做了這樣的一道題：

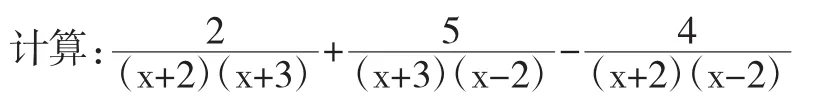
請三位同學上黑板解，其中一位同學的解法是：

解：原式=2（x-2）+5（x+2）-4（x+3）=3x-6

他的解法顯然錯了。當教師點評到這位同學的解法時，引來了下面學生的一些嘲笑。教師問其他同學：“他這道題的解法錯在哪呢？”這下，課堂氣氛一下子活躍起來了，同學們七嘴八舌地說：“他把分式方程變形（去分母）搬到計算題上了，結果丟了分母。”這位同學一下子紅了臉，不好意思地低下了頭。這時教師對同學的說法不予置評，沉思了一會兒，干脆來個“將錯就錯”。“剛才這位同學把計算題當作方程來解了，雖然解法錯了，但是給了我們一個啟示，若能將該題去掉分母來解，其‘解法’確實簡潔明快，因此，我們能否考慮利用解分式方程的解法來解它呢？”教師這么一說，剛才這位同學的頭也慢慢地抬了起來。“一石激起千層浪”，其他同學也紛紛議論起來，尋找解決問題的新方法。在大家的踴躍探求下，一個新的解法也就誕生了。

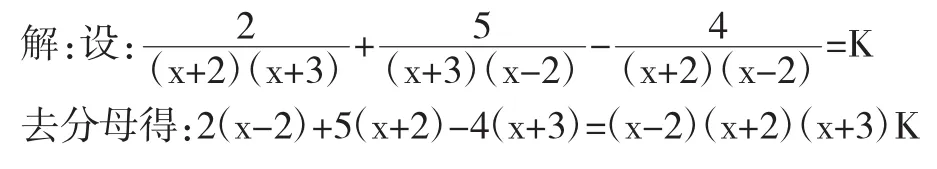
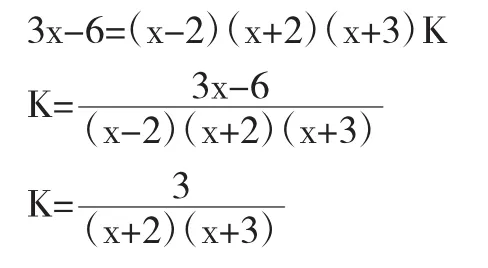
學生很開心：“我們又掌握了一種新的解法，太好了。”大家都體驗到了成功的喜悅。教師接著又對這位同學作了激勵性的評價：“剛才，你的解法雖然錯了，但你的這種‘用方程的思想解分式計算題’的思想卻是一種尋求簡便的思想，是自己思維的真實展示，給了我們有益的啟示。”這位同學的臉上也露出了笑容，臉上洋溢著自信。令教師沒想到的是，這位同學以后上數學課都特別的認真，而且信心十足，對數學也分外的喜愛，上課更是大膽發言，對有些問題的解決也常常有自己的獨到之處。

二、錯例是加深理解基礎知識的重要手段

學生新學一個定義、法則、公式和性質的時候，往往把其間的關鍵性詞語忽略或對其符號意義不明而造成錯誤，這時的錯例就成了加深理解和記憶的重要手段。

例如，在利用配方法解一元二次方程時，教師出示了以下例題：

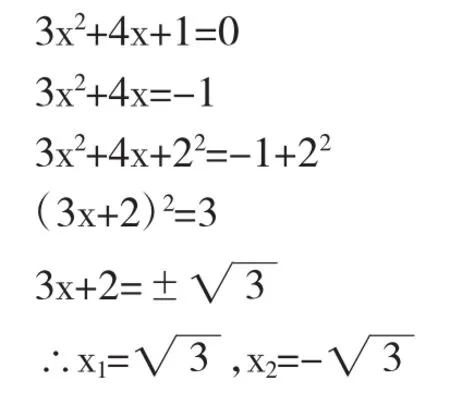
教師讓學生仔細觀察后問：“以上解答過程是否正確？若不正確，請同學們找出錯誤原因，并做出正確解答。”在觀察過程中許多不細心的學生根本看不出破綻，感到很疑惑，都產生了想得到正確答案的渴望，教師讓學生思考幾分鐘后，叫一位學習成績優異的學生在錯例旁板出正確的解答過程：

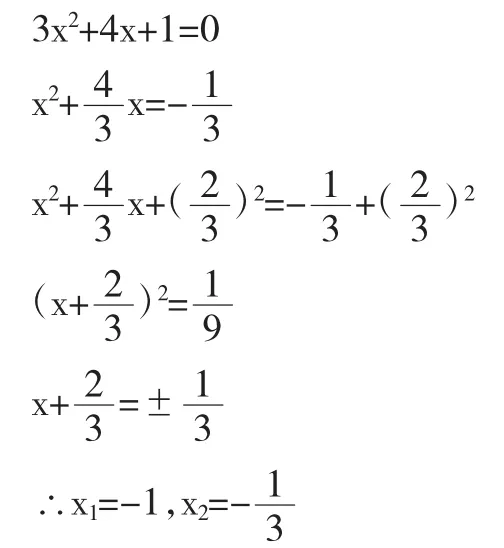
教師讓學生觀察、比較錯例和正例，通過觀察、比較不難看出，錯例在解答過程中沒有先將二次項系數化為1，學生因此牢牢記住了在利用配方法解一元二次方程時，應先將二次系數化為1，加深理解和掌握解題方法。

三、錯例是糾正錯誤的常用方法

對一些學生在認識上的模糊，從正面又難以說清的問題，教師能舉出一個或幾個生動而擊中要害的錯例，引導學生討論，往往能收到比較好的效果。

例如，在七年級學生學習數軸時，教師畫了這樣一條數軸：

圖1

問：“這是數軸嗎？”班級同學幾乎異口同聲大聲回答：“不是數軸！”一個個顯得得意的樣子，這答案很明顯錯了，他們總認為數軸哪有這么簡單，所為數軸應該要像這樣（如下圖）：

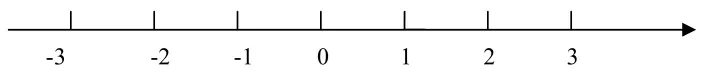
數軸既要有負坐標又要有正坐標，他們對數軸的“三要素”理解還不夠透徹，所以教師又問：“真不是嗎？”他們還是回答：“不是！”教師說：“好，下面請同學們在圖1中找出原點、正方向和單位長度。”通過教師幫忙，同學們很快就找出了圖1中數軸的“三要素”，同時也確認了圖1是數軸，并很好地掌握了關于數軸的基礎知識。

往往像以上這樣的問題，教師通過設置錯例的方式來幫助學生鞏固知識，對學生糾正答題中的錯誤肯定很有幫助。

四、錯例是發現問題的重要途徑

教師講清了概念，學生記住了概念，并不等于真正理解和掌握了概念，還要通過計算和解題實踐來加以檢驗。教師精心設計一些易錯題讓學生練習，是一個發現教學上存在問題的重要途徑。

例如，在一元二次方程這一章解題中，往往學生容易忽略二次項系數a≠0及最高次數為2次的方程，所以教師可設計易錯題如：若方程（m-2）x（m2-2）-4x+3=0是一元二次方程，則m滿足條件：____。在教學過程中很多學生會只考慮m2-2=2，得出答案是m=±2，這時教師問：請m=2把帶回方程看看，學生就會發現二次項為0，才知道m-2≠0這一條件，即二次項系數a≠0，所以本題m只能為-2，不能為2.

又如，在教學“三角形的內角和”練習中，教師在黑板上出示下面三組角：

第一組∠1=35°，∠2=75°，∠3=70°；

第二組∠1=15°，∠2=25°，∠3=60°；

第三組∠1=100°，∠2=65°，∠3=90°。

要求學生分別做出這三個三角形。片刻之后，學生做成了第一個三角形。但按第二組和第三組的條件，無論如何也不能做成三角形。學生頓生疑團，議論紛紛，不知所措，急需求教于教師。這時，教師讓學生分別畫一個直角三角形、銳角三角形和鈍角三角形，量一量它們的三個角，看一看三角形內角和有什么規律。這樣，通過測量、驗證，學生恍然大悟，原來三角形的內角和是180°，而二、三組兩個三角形的內角和不等于180°，所以無法做出這兩個三角形。

利用錯誤拓展師生共同成長的空間，使課堂中的錯誤成為一種重要的課程資源，這是新課程改革背景下教師促進學生學習、達成教學目標的必由之路。當我們以滿腔的熱情，嚴謹的態度，科學的方法來對待、親近它時，它將給我們呈現教學的革新。

G632.0

A

1674-9324（2014）21-0084-02