長壽指數(shù)延遲年金的設(shè)計與價值測度

2014-06-28 02:58:14張元萍王力平

當(dāng)代經(jīng)濟科學(xué) 2014年2期

張元萍，王力平

(天津財經(jīng)大學(xué)經(jīng)濟學(xué)院，天津300222)

一、引言

人口預(yù)期壽命的普遍延長使“生命周期假說”中退休階段的財富配置得到越來越多的關(guān)注，退休人員的財富衰減計劃(wealth decumulation)逐漸成為個人理財中的重要課題。年金作為養(yǎng)老金融產(chǎn)品，在老年人的生存期間定期提供支付以支撐其晚年消費，即在保證了老年人每期消費的同時覆蓋了全部的長壽風(fēng)險。然而，現(xiàn)實中各國的年金市場發(fā)展的并不繁榮——這就是所謂的“年金之謎”。“年金之謎”的形成有兩個方面的原因:第一，需求不旺盛:年金損害了老年人的流動性偏好和遺產(chǎn)動機，同時年金的價格很高;第二，供給非意愿:逆向選擇的長期存在以及長壽風(fēng)險的凸顯，限制了壽險公司對年金的供給。雖然學(xué)術(shù)界討論了兩種壽險公司管理長壽風(fēng)險的途徑:再保險和對沖，但是這兩種方法都會提高管理費用，使年金價格進一步升高;此外，這兩種方法的管理效果還沒有得到充分的現(xiàn)實考證。本文旨在通過長壽指數(shù)延遲年金(LIDA)的設(shè)計，一方面轉(zhuǎn)移年金提供者承擔(dān)的長壽風(fēng)險，另一方面，為年金購買者提供價格較低的多樣化長壽風(fēng)險覆蓋率的年金產(chǎn)品。

長壽指數(shù)延遲年金(Longevity-Indexed Deferred Annuities)，是一種指數(shù)化變額年金產(chǎn)品，實現(xiàn)了長壽風(fēng)險在年金提供者和購買者之間的轉(zhuǎn)移和分擔(dān)。以實際存活率與參照存活率的比值作為長壽指數(shù)，表征系統(tǒng)性長壽風(fēng)險。年金供給者將每期支付與長壽指數(shù)掛鉤，將(部分)系統(tǒng)性長壽風(fēng)險轉(zhuǎn)移給年金購買者。年金供給者承擔(dān)(部分)系統(tǒng)性長壽風(fēng)險、非系統(tǒng)性長壽風(fēng)險(根據(jù)大數(shù)定律可充分分散)和利率風(fēng)險。對購買者而言，LIDA的長壽風(fēng)險覆蓋率不再是100%，而是自身承擔(dān)了一部分系統(tǒng)性風(fēng)險，因此價格較低。本文利用保險精算和動態(tài)優(yōu)化數(shù)值方法計算一系列LIDA的價格和長壽風(fēng)險覆蓋率，購買者可以根據(jù)自己的遺產(chǎn)動機、流動性要求等選擇不同風(fēng)險覆蓋率和價格的LIDA產(chǎn)品。

二、文獻綜述

從長壽風(fēng)險分擔(dān)的角度，學(xué)者們研究了很多類型的年金產(chǎn)品。第一類是群體自年金化(GSA)或長壽風(fēng)險池年金(longevity-risk pooling fund)。這一類年金最早由 Wadsworth et al［1］提出，之后 Piggott et al［2］進行細(xì)致分析。GSA的風(fēng)險分擔(dān)模式是年金持有人承擔(dān)系統(tǒng)性風(fēng)險，年金池負(fù)責(zé)分散非系統(tǒng)性長壽風(fēng)險，而年金提供者，在一定意義上來講，不承擔(dān)任何風(fēng)險。Piggott et al［2］推導(dǎo)了構(gòu)成GSA價格的兩個調(diào)整因子在單一群體年金池、異質(zhì)群體年金池和死亡率預(yù)期改變等情況下的具體形式和支付路徑。Qiao和 Sherris［3］利用極值理論計算存活率的分布和年金價格，并在此基礎(chǔ)上測度GSA的風(fēng)險池化效率，并量化了年金池的規(guī)模對風(fēng)險分擔(dān)的影響。第二類年金產(chǎn)品是與死亡率有關(guān)的指數(shù)型年金。Richter和Weber［4］設(shè)計了死亡率指數(shù)年金并比較了傳統(tǒng)年金與死亡率指數(shù)年金對購買者的吸引力。 Denuit et al［5］提出了長壽指數(shù)年金，年金的支付與系統(tǒng)性長壽風(fēng)險的轉(zhuǎn)移都與長壽指數(shù)相關(guān)，并對轉(zhuǎn)移的比例設(shè)定了上下限，這樣設(shè)計既能減輕年金供給者的負(fù)擔(dān)又能保證對年金購買者的長壽風(fēng)險覆蓋。

從消費者購買年金價格的角度開發(fā)年金產(chǎn)品，代表性的主要是Milevsky［6］年提出的通脹調(diào)整型延遲年金(ALDA)。這種年金在高齡階段(如80歲以后)才產(chǎn)生支付，價格低于普通年金，但能提供高齡階段的全部風(fēng)險覆蓋。Scott［7］利用保險價值原理分析了一類適合于不愿意完全年金化的老年人的年金產(chǎn)品——長壽年金，即延遲支付的年金。數(shù)值計算認(rèn)為，用10%的財富購買長壽年金所得收益高于50%財富分配在即期年金上所得到的的收益。在ALDA的基礎(chǔ)上，Huang et al［8］開發(fā)了破產(chǎn)或有生命年金RCLA，其支付要延遲到一個預(yù)設(shè)的金融擴散過程的觸零時刻才產(chǎn)生，文章用數(shù)值方法在一系列現(xiàn)實的參數(shù)下為RCLA定價。

Mitchell et al［9］在《美國經(jīng)濟評論》雜志上發(fā)表了一篇關(guān)于個人年金貨幣價值的文章。為計算年金的保險價值，文章比較了退休人員年金化和非年金化兩種模式下的消費效用，并利用兩種模式下達到相同最優(yōu)效用時的財富比值作為年金保險價值的測度指標(biāo)。Brown和Poterba［10］同樣提到了“年金等價財富”的概念，即為了得到與全部年金化相同的效用，消費者至少需要多少倍的非年金化財富。Gong和Webb［11］利用ADLA的年金等價財富與即期年金等價財富的比值作為衡量ADLA的長壽風(fēng)險覆蓋率的指標(biāo)，計算結(jié)果顯示，在購買人85歲時，ADLA在滿足了購買人流動性要求的同時，提供了高于50%的長壽風(fēng)險覆蓋。

綜上所述，GSA將所有長壽風(fēng)險轉(zhuǎn)移給購買者承擔(dān)，對于風(fēng)險厭惡型投資者的吸引力不大;長壽指數(shù)年金通過設(shè)定上下限的方式約束了系統(tǒng)性風(fēng)險的轉(zhuǎn)移比例，具有一定合理性。本文在設(shè)計長壽指數(shù)時，從購買者的角度考慮，只設(shè)定年金支付的下限。由于長壽風(fēng)險一般在75歲之后才開始顯現(xiàn)，所以延遲年金相比即期年金而言可能將會更受投資者青睞。本文綜合以上兩種年金的支付形式，創(chuàng)新性地提出長壽指數(shù)延遲年金，同時滿足了年金提供者的長壽風(fēng)險轉(zhuǎn)移和年金購買者的長壽風(fēng)險覆蓋。

三、長壽風(fēng)險的轉(zhuǎn)移——LIDA的設(shè)計與定價

長壽指數(shù)延遲年金包含了延遲年金和長壽指數(shù)年金這兩種年金的支付特征。因此，為了更好的闡述LIDA，我們先分別探討即期年金(SPIA)、延遲年金(ALDA)和長壽指數(shù)年金(LIA)的設(shè)計與定價，然后構(gòu)建LIDA的定價公式，最后做數(shù)值計算。

1.即期年金與延遲年金

即期年金(Single-Premium Immediate Annuity)是最簡單的年金形式，退休人員在x歲購買，從即期開始定期支付。在不確定生命周期下分析，x歲的人的預(yù)期余命用Tx表示，由生存概率tpx決定。因此，每期支付1元的即期年金的價格為:

延遲年金(Advanced-Life Delayed Annuity)是指老年人在x歲時購買，在x+τ歲時開始支付。從這個意義上講，即期年金是延遲年金的特例，即當(dāng)τ=0時，延遲年金就退化成了即期年金。根據(jù)定義，1元延遲年金的價格為:

從另一個定價的角度看，ALDA的價格可以理解為將在x+τ歲購買的SPIA貼現(xiàn)到x歲時的價值，即:

從(3)式可以看出，延遲年金的價格要小于即期年金的價格。

2.長壽指數(shù)年金

長壽指數(shù)年金的每期支付不再是定值，而是與真實存活率的預(yù)測值相關(guān)。真實存活率預(yù)期對參照存活率的偏離即為系統(tǒng)性長壽風(fēng)險。利用長壽指數(shù)L表征系統(tǒng)性長壽風(fēng)險:

tpx表示真實存活率的預(yù)測值，通過死亡率模型估算得到。表示參照存活率，由人壽保險生命表計算得到。當(dāng)死亡率普遍下降，真實存活率上升，長壽指數(shù)增大，年金產(chǎn)品的系統(tǒng)性長壽風(fēng)險增大。為了轉(zhuǎn)移系統(tǒng)性長壽風(fēng)險，LIA每期的支付設(shè)定為1/L，即當(dāng)預(yù)期存活率上升時，LIA的支付下降。

然而，年金購買者不愿意承擔(dān)全部系統(tǒng)性長壽風(fēng)險，為了保證年金購買者的收益，本文設(shè)定年金支付的下限(如floor=0.8)，此時，長壽指數(shù)年金的價格為:

由于死亡率普遍下降，長壽指數(shù)幾乎不可能大于1，因此，與即期年金相比，長壽指數(shù)年金的價格更低。同一年齡和利率下，LIA與SPIA的差別便可以作為年金供給者轉(zhuǎn)移給購買者的系統(tǒng)性長壽風(fēng)險的度量。

3.長壽指數(shù)延遲年金

綜合以上LIA與ALDA的支付特征，可以推導(dǎo)出LIDA的單位年金價格:

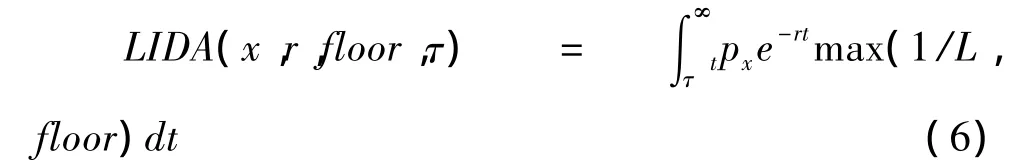
從公式來看，LIDA的價格比LIA更低，因此相較傳統(tǒng)的SPIA，LIDA在價格上更具吸引力。這一點我們將在下文的數(shù)值計算中充分體現(xiàn)。

需要說明的是，在傳統(tǒng)年金中，年金提供者承擔(dān)所有風(fēng)險——利率風(fēng)險、系統(tǒng)性和非系統(tǒng)性長壽風(fēng)險。非系統(tǒng)性長壽風(fēng)險可以通過大量的年金合同進行分散，利率風(fēng)險和系統(tǒng)性長壽風(fēng)險是年金提供者風(fēng)險管理的重點。為了闡述和計算簡便，本文暫時不考慮利率風(fēng)險，將利率設(shè)定為常數(shù)，單純考慮系統(tǒng)性長壽風(fēng)險的轉(zhuǎn)移和覆蓋在年金價格中的體現(xiàn)。

4.數(shù)值計算

(1)參數(shù)設(shè)定

首先，本文利用尚勤［14］構(gòu)造的死亡強度對生存概率進行預(yù)測，具體形式為:

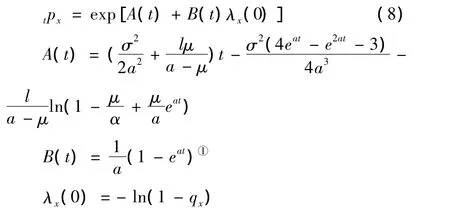
其中，λx(t)為x歲人口在第t年的死亡強度，服從帶跳躍的OU過程:

式中Wλ(t)表示標(biāo)準(zhǔn)布朗運動，本文假定死亡率與金融資產(chǎn)收益率相互獨立，因此Wλ(t)與Wrt不相關(guān)。J(t)是純復(fù)合泊松跳躍過程，泊松到達強度為l＞0，跳躍幅度服從指數(shù)分布，其均值μ＜0。假設(shè)布朗運動、泊松過程和跳躍過程相互獨立。

利用《中國人壽保險業(yè)經(jīng)驗生命表(2000-2003)》中養(yǎng)老金業(yè)務(wù)男表的數(shù)據(jù)估計出參數(shù)值為:μ =-0.00038，a=0.07698，l=0.00256，σ =0.00031［14］。qx為死亡率，由生命表查得。通過(8)式可以計算x歲的男性人口在未來生存期間(105-x)年的存活率(生命表中的最大年齡為105歲)。

2019年，我們啟動了第二輪改版升級，增加頁碼，優(yōu)化欄目，快遞寄刊。在自我反思中完善，在創(chuàng)新服務(wù)中前行。

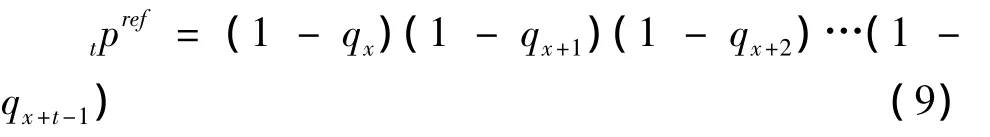
最后，利率設(shè)為定值，r分別取0.03，0.04，0.05。在計算LIDA價格時，年金支付下限分別設(shè)定為floor=0.8，0.7，0.6。延遲時間分別設(shè)定為 τ=10，15，20，25，30。

(2)本文利用數(shù)值法在離散時間下計算60歲男性人口購買年金的價格，結(jié)果如表1。

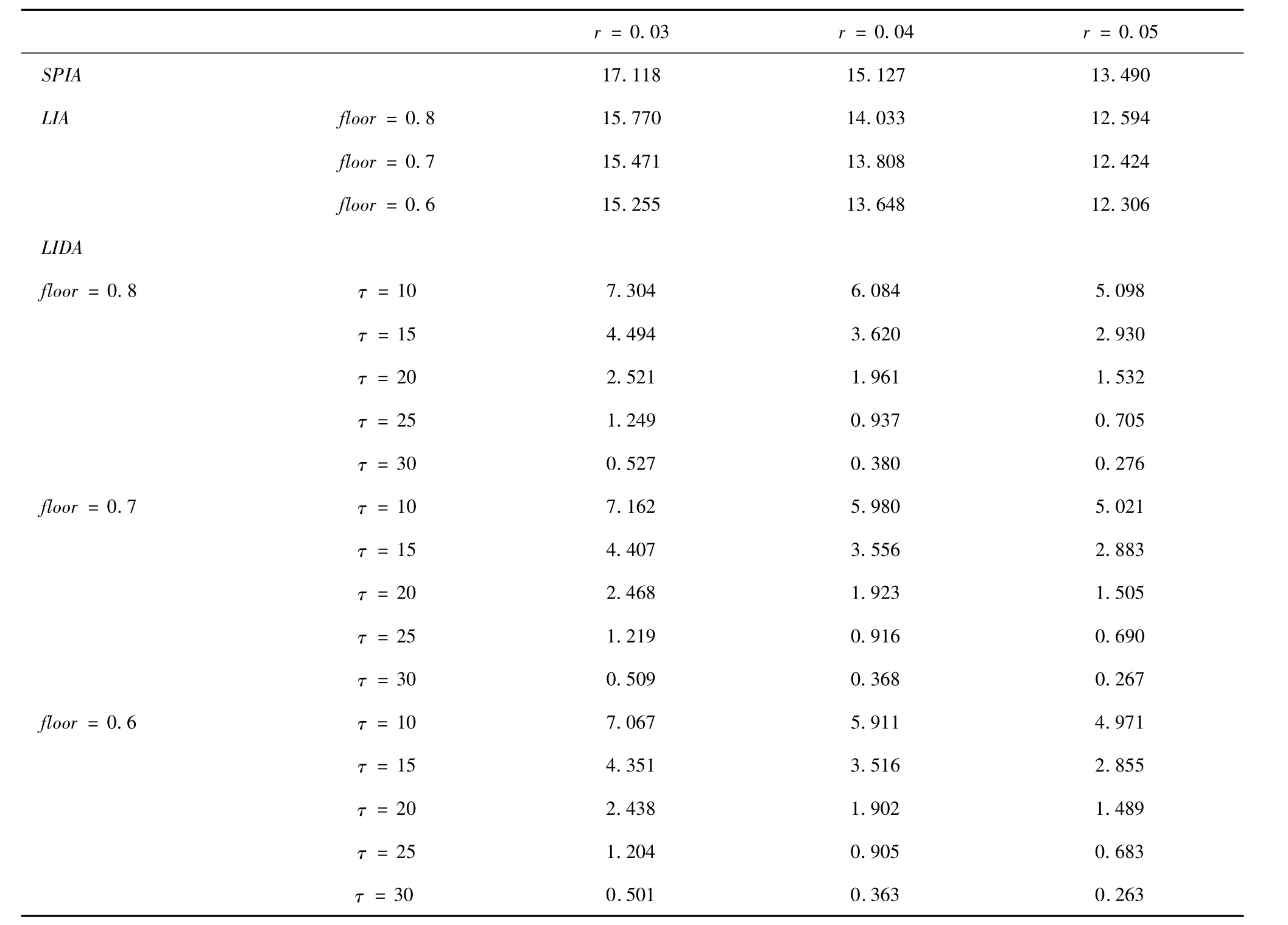
表1 LIDA年金價格

從總體上看，折現(xiàn)利率增大，年金的價格減小。以r=0.03為例，比較各類年金的價格。為獲得1元即期年金，需躉交17.118元;而若購買長壽指數(shù)年金，價格降低到15.255～15.770元;如果購買LIDA，價格有更大幅度的下降:下限0.8，70歲起付的年金價格為7.034元，較即期年金下降了57.3%。從年金支付的下限進行比較，下限越低，每期保證支付的金額就少，因此年金價格也降低，但不同下限的年金價格差別不大，因為下限之間的差別經(jīng)折現(xiàn)之后體現(xiàn)在年金價格上就不明顯了。從延遲時間來看，隨著τ增大，年金價格不斷下降，而且下降幅度越來越大，下限0.8，90歲起付的年金價格僅為0.527元。退休人員的個人長壽風(fēng)險一般在75歲開始顯現(xiàn)，因此，單獨從價格上考慮，以4.494元購買下限0.8，75歲起付的LIDA對消費者來說更有吸引力。

(3)系統(tǒng)性長壽風(fēng)險的轉(zhuǎn)移測度。

年金購買者因承擔(dān)了一部分系統(tǒng)性長壽風(fēng)險而獲得價格較低的年金，本文利用LIA、LIDA與SPIA的年金價格相比的降低幅度粗略地量化轉(zhuǎn)移了的系統(tǒng)性長壽風(fēng)險。風(fēng)險分擔(dān)情況如圖1所示。

從圖1的數(shù)據(jù)中我們可以分析出兩個特點:第一，LIA的設(shè)計目的就是要幫助年金供給者轉(zhuǎn)移系統(tǒng)性長壽風(fēng)險，從數(shù)值上看，轉(zhuǎn)移幅度大概為7%左右，達到了預(yù)期的目的。第二，LIA(τ=0)的長壽風(fēng)險轉(zhuǎn)移率隨著折現(xiàn)率r的增大而減小，而LIDA的長壽風(fēng)險轉(zhuǎn)移率隨著折現(xiàn)率r的增大而增大。這說明雖然每類年金的價格都是隨著折現(xiàn)率的上升而下降，但LIDA的年金價格下降的幅度更大。第三，LIDA的系統(tǒng)性長壽風(fēng)險轉(zhuǎn)移的幅度很大，延遲10年支付，可以轉(zhuǎn)移一半以上的系統(tǒng)性長壽風(fēng)險;當(dāng)延遲時間為30年時，可以轉(zhuǎn)移95%以上的系統(tǒng)性長壽風(fēng)險。因此，從年金提供者的角度，發(fā)行L I D A是進行長壽風(fēng)險管理的一個有效有簡捷的途徑。

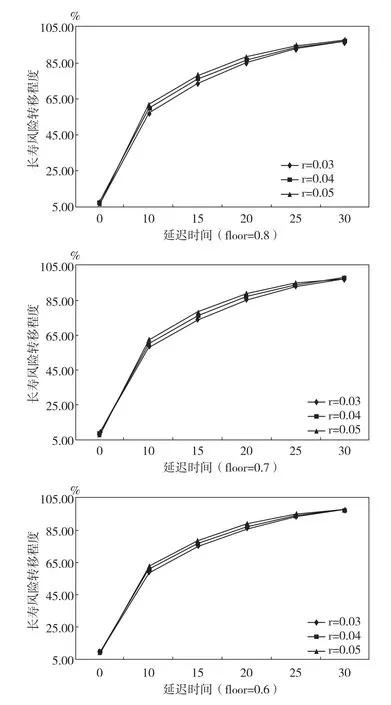
圖1 長壽風(fēng)險延遲程度

四、長壽風(fēng)險的覆蓋——L I D A保險價值的計算

年金對長壽風(fēng)險的保險價值可以用年金的等價財富來度量。退休人員的財富衰減計劃大體上有兩種選擇：年金化和非年金化。假定在非年金化模式下初始財富為W0，老年人通過合理安排自己的消費達到了最大化效用U*，為了達到相同的效用U*，老年人需要進行年金化的財富為 Weq。定義 α=W0/Weq為年金等價財富系數(shù)，即1單位年金化的財富等價于α單位的非年金化的財富。由于年金的保險作用，所以α大于1，因而年金的保險價值體現(xiàn)為為達到相同的效用，老年人需要增加多少非年金化財富，即α-1。

上文中提到，即期年金對長壽風(fēng)險的覆蓋率是100%，因此，L I D A的長壽風(fēng)險的覆蓋率可以通過比較L I D A與即期年金的保險價值獲得。

1.分析框架

假定老年人在60歲有一定量初始財富，未來沒有收入來源，老年人通過選擇財富衰減策略最大化晚年效用。本文采用時間可加的效用函數(shù)來描述：

其中，消費效用采用了C R R A效用函數(shù)形式，γ表示相對風(fēng)險厭惡系數(shù)。ρ表示時間偏好。

（1）當(dāng)老年人選擇非年金化時，每期的財富約束如下：

（10）、（11a）和（11b）式組成了動態(tài)最優(yōu)化模型，通過對模型的求解，可以得出最優(yōu)消費路徑和最大化效用U*。

（2）當(dāng)老年人購買即期年金或長壽指數(shù)年金時，每期的財富約束如下：

假定老年人將全部財富年金化，手中所剩財富W0=0，之后每期都會獲得At的支付。當(dāng)老年人購買即期年金時，At為定值；當(dāng)老年人購買L I A時，At與長壽指數(shù)有關(guān)。求解（10）、（12a）和（12b）構(gòu)成的動態(tài)優(yōu)化模型，找出滿足m a x U=U*時的每期支付進而計算 Weq：

ax表示某一類型年金（SP I A、L I A、L I D A）的價格。通過以上求解得出和。

（3）當(dāng)老年人購買L I D A時，財富縮減過程包括兩個階段：年金起付時刻之前的自主安排和年金支付期定期獲得支付。因此，效用的計算也分為兩個階段。出于簡單考慮，本文假定，在起付期之前，老年人按照（1）中的最優(yōu)消費路徑進行消費，并得到相應(yīng)的效用。在年金支付期，動態(tài)優(yōu)化模型變化如下:此時，需計算滿足 maxU =U*-U*1 的At)。

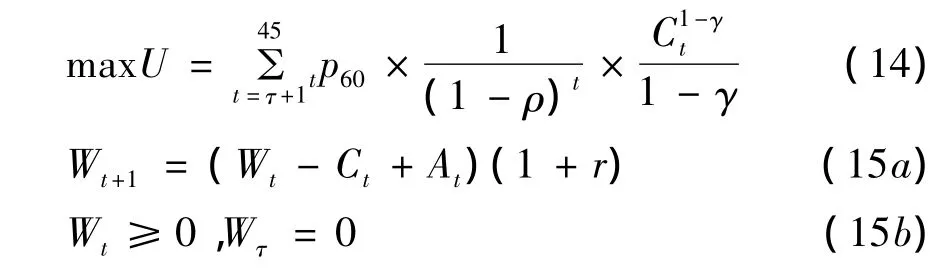
(4)計算長壽風(fēng)險覆蓋率。

通過以上計算，可以分別得到即期年金、LIA和LIDA的保險價值如下:

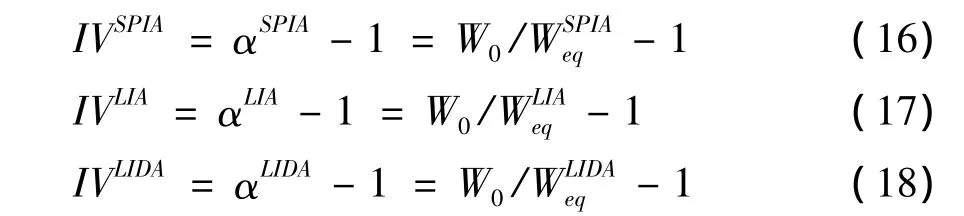
即期年金覆蓋了全部長壽風(fēng)險，因此，其長壽風(fēng)險覆蓋率為100%。其他年金的長壽風(fēng)險覆蓋率(longevity-risk coverage)可以與之比較得到:

2.數(shù)值計算

假定參數(shù) ρ=0.05，r=0.03，本文利用離散時間下動態(tài)最優(yōu)化數(shù)值方法進行實證分析。

(1)LIA長壽風(fēng)險覆蓋率計算結(jié)果如表2。

表2 LIA的等價財富系數(shù)和長壽風(fēng)險覆蓋率

以往很多研究表明，年金對風(fēng)險規(guī)避型消費者而言價值更大，這個結(jié)論在表3中也能體現(xiàn)。同樣提供100%風(fēng)險覆蓋的即期年金，對γ=3的消費者而言，1單位年金化財富相當(dāng)于1.609單位的非年金化財富，而對γ=7的消費者而言，等價財富系數(shù)上升到1.655。由于LIA存在著系統(tǒng)性長壽風(fēng)險轉(zhuǎn)移，因此其等價財富系數(shù)均小于即期年金，而且隨著年金支付下限的降低，年金的等價財富系數(shù)減小。

長壽風(fēng)險覆蓋率是根據(jù)等價財富系數(shù)計算獲得的，因此對不同風(fēng)險偏好的消費者來說，同一年金的長壽風(fēng)險覆蓋率不同，從這個意義上講，這是一個相對主觀的指標(biāo)。同一年金對于γ=3和γ=7的消費者的長壽風(fēng)險覆蓋率相差2%～3%。從整體結(jié)果來看，LIA能夠為年金購買者提供80%以上的長壽風(fēng)險覆蓋。

(2)LIDA長壽風(fēng)險覆蓋率的計算。年金保險價值與消費者風(fēng)險規(guī)避系數(shù)的關(guān)系在表3中已經(jīng)得到體現(xiàn)，在此僅以γ=3為例對LIDA長壽風(fēng)險覆蓋率進行闡述，如圖2所示。

當(dāng)消費者的風(fēng)險規(guī)避系數(shù)一定時，LIDA的長壽風(fēng)險覆蓋率沿著兩個維度變化:一是隨著支付下限的降低而降低，二是隨著延遲時間的延長而降低，而且降低的幅度越來越大。從計算結(jié)果來看，當(dāng)延遲時間不超過20年時，LIDA能夠提供50%以上的長壽風(fēng)險覆蓋。當(dāng)老年人選擇75歲起付的下限為0.8的LIDA時，其獲得的長壽風(fēng)險覆蓋為65.62%;結(jié)合表1的價格數(shù)據(jù)，75歲的老年人以26.25%(4.494/17.118)的價格獲得65.62%的長壽風(fēng)險覆蓋，其余的34.38%的長壽風(fēng)險由節(jié)省下來73.75%的非年金化財富覆蓋，這樣可以既保證了一定程度的長壽風(fēng)險覆蓋，又使老年人手中留有較多的流動性財富供其支配。此外，本文的分析是基于老年人在退休期間沒有任何其他收入來源的假設(shè)之上的，當(dāng)老年人存在其他收入來源，如退休金、社保金、繼續(xù)工作的報酬、兒女贍養(yǎng)費等，那么在本文提供的一系列LIDA中，老年人將會有更大的選擇空間。

圖2 LIDA長壽風(fēng)險覆蓋率

五、結(jié)論及展望

本文從養(yǎng)老金融產(chǎn)品創(chuàng)新的角度，緩解了年金的供給和需求的矛盾:在轉(zhuǎn)移了年金供給人的部分系統(tǒng)性長壽風(fēng)險的同時，為年金購買者提供了具有一定長壽風(fēng)險覆蓋的更低價格的年金產(chǎn)品——長壽指數(shù)延遲年金(LIDA)。

在年金產(chǎn)品中，年金供給者承擔(dān)利率風(fēng)險、系統(tǒng)性長壽風(fēng)險和非系統(tǒng)性長壽風(fēng)險。利率風(fēng)險是任何金融產(chǎn)品都會包含的風(fēng)險，非系統(tǒng)性長壽風(fēng)險可以根據(jù)大數(shù)定律進行分散，而系統(tǒng)性長壽風(fēng)險才是年金供給者真正的挑戰(zhàn)。再保險和長壽風(fēng)險對沖產(chǎn)品都是管理長壽風(fēng)險的合理途徑。然而，再保險市場的成熟程度限制了年金供給者進行再保險的可能;而長壽風(fēng)險的對沖對產(chǎn)品參數(shù)的設(shè)定、市場成交量、資本市場發(fā)達程度等都有很高的要求。長壽指數(shù)延遲年金，通過設(shè)定長壽指數(shù)將系統(tǒng)性長壽風(fēng)險部分轉(zhuǎn)移給年金購買者，轉(zhuǎn)移程度隨著下限的降低和延遲時間的延長而增大。這樣，既豐富了老年人的產(chǎn)品選擇，又有效地減輕了年金供給者的風(fēng)險負(fù)擔(dān)。實證結(jié)果顯示，本文設(shè)定的三款下限為0.8～0.6的LIDA均能夠轉(zhuǎn)移50%以上的系統(tǒng)性長壽風(fēng)險。

老年人制定財富衰減計劃時會在年金化和非年金化之間躊躇，實質(zhì)上是在購買年金的代價和長壽風(fēng)險覆蓋之間進行衡量。即期年金可以為老年人提供100%的長壽風(fēng)險覆蓋，但代價是很高的年金價格以及損害了老年人的流動性需求和遺產(chǎn)需求。本文在梳理計算各類年金(SPIA、LIA、LIDA)的價格之后，引入年金等價財富的概念，利用動態(tài)最優(yōu)化數(shù)值算法求解不同種類年金的長壽風(fēng)險覆蓋率。計算結(jié)果表明，長壽指數(shù)年金可以以較低價格提供80%以上的長壽風(fēng)險覆蓋，而LIDA為老年人提供了一系列更低價格、不同長壽風(fēng)險覆蓋程度的產(chǎn)品，使老年人在長壽風(fēng)險覆蓋率、流動性需求和遺產(chǎn)動機之間有更大的權(quán)衡空間。

［1］ Wadsworth M，F(xiàn)indlater A，Boardman T.Reinventing annuities［R］.The Staple Inn Actuarial Society Working Paper，2001.

［2］ Piggott J，Valdez E A，Detzel B.The simple analytics of pooled annuity fund［J］.Journal of Risk and Insurance ，2005，72(3):497-520.

［3］ Qiao Chao，Sherris M.Managing systematic mortality risk with group self pooling and annuitisation schemes［R］.ARC Centre of Excellence in Population Ageing Research(CEPAR)Working Paper，2011.

［4］ Richter A ，Weber F.Mortality-indexed annuities:Managing longevity risk via product design［R］.Discussion Paper of Munich School of Management，University of Munich，2009 .

［5］ Denuit M，Haberman S，Renshaw A.Longevity-indexed life annuities［J］.North American Actuarial Journal，2011，15:97-111.

［6］ Milevsky M A.Real longevity insurance with a deductible:Introduction to advanced-life delayed annuities(ALDA)［J］.North American Actuarial Journal，2005，9(4):109-122.

［7］ Scott J S.The longevity annuity:An annuity for everyone?［J］.Financial Analysts Journal，2008，64(1):40-48.

［8］ Huang Huaxiong，Milevsky M A，Salisbury T S.Valuation and hedging of the ruin-contingent life annuity(RCLA)［J］.Journal of Risk and Insurance，2013，80(1).

［9］ Mitchell O S，Poterba J M ，Warshawsky M J，Brown J R.New evidence on the money′s worth of individual annuities［J］.American Economic Review，1999，89(5):1299-1318.

［10］ Brown J R，Poterba J M.Joint life annuities and annuity demand by married couples［J］.Journal of Risk and Insurance，2000，67(4):527-554.

［11］ Gong Guan，Webb A.Evaluating the advanced life deferred annuity-An annuity people might actually buy［J］.Insurance:Mathematics and Economics，2010，46:210-221.

［12］ Horneff W J，Maurer R H，Stamos M Z.Life-cycle asset allocation with annuity markets:Is longevity insurance a good deal?［R］.University of Michigan，Michigan Retirement Research Center Working Paper，2006.

［13］ Blake D，Cairns A，Dowd K，MacMinn R.Longevity bonds:Financial engineering，valuation and hedging［J］.Journal of Risk and Insurance ，2006，73:647-72.