國際費雪效應在東亞地區存在嗎——基于中國視角的探究

江 春，陳 永，江 鵬

(1.武漢大學金融發展研究中心，湖北武漢430072;2.武漢大學經濟與管理學院，湖北武漢430072;3.英國伯明翰大學商學院，英國伯明翰B15 2TT)

一、引 言

20世紀90年代以來，東亞地區的高速發展吸引了大量國際資本的流入，這極大地促進了東亞各國家(地區)金融自由化改革，加強了東亞地區內部的經濟聯系。中國在這一區域的經濟影響力也與日俱增，隨著我國利率市場化改革進入實質階段，一個自然的問題是:我國利率是否已經成為東亞地區的“驅動利率”?考察國際費雪效應是否在這一區域成立為這一問題提供了思路，對國際費雪效應的研究事實上是對實際利率平價的研究，其本質是判斷各國相對中國的實際利差是否收斂到一個平穩的過程。國際費雪效應認為，在金融市場主體存在理性預期、可以自由套利且不考慮交易成本的情況下，兩國實際利差應該趨于零。由于市場中普遍存在的交易成本和資本管制，實際利率往往并不一致，在長期中實際利差會收斂到一個不為零的常數，在這種情況下，我們認為非嚴格的國際費雪效應成立。國際費雪效應在理論和實踐操作中都具有重要的意義。首先，由于這一效應將非拋補利率平價和相對購買力平價結合起來，反映了兩國之間名義利率、通貨膨脹率和實際利率的聯系，從而在理論上提供了一種綜合視角以重新審視國際經濟關系。其次，由于國際費雪效應本質上反映了兩國間實際利率的差異，從而成為衡量經濟一體化程度的重要指標。國際費雪效應在匯率決定理論中是一個關鍵的假定，Frenkel［1］和 Mussa［2］在他們的匯率模型中認為實際利率平價在長期中是成立的。那么這一效應在東亞地區成立嗎?本文將借助于一種不同于以往研究國際費雪效應的計量手段——傅立葉函數的單位根方法，對東亞地區的國際費雪效應進行檢驗。

二、文獻綜述

為了檢驗國際費雪效應，國外學者采用的方法主要有以下幾種:

第一種是線性回歸的方法。這種方法早在二十世紀八十年代就已經被許多學者使用(如Mark)，他們將兩個國家實際利率分別作為控制變量和被控制變量構建回歸方程，如果控制變量系數不顯著異于1，方程常數項不顯著異于0，則說明兩國間存在國際費雪效應［3］。這些早期研究存在一定局限性，原因在于沒有對所用的時間序列數據進行平穩性檢驗，因此這種方法后來被 Goldberg et al.［4］進行了改進。他們在構建一階自回歸模型之前對回歸數據進行了平穩性檢驗，這樣就避免了由于外部沖擊造成的數據不平穩性的干擾，更重要的是他們將匯率制度變化的結構性突變點引入了模型中。

第二種是協整檢驗法。協整檢驗主要適用于非平穩的時間序列的情況。Engle＆Granger的E－G法，Johansen＆Juselius的J－J法分別用于描述單變量和多變量的協整關系。這兩種方法都得到了較為廣泛的應用，而且學者們運用這兩種方法研究同一問題通常可以得到相似的結論。

第三種方法是單位根檢驗法。單位根檢驗方法的原理是平穩時間序列在受外部沖擊后會向其均值回歸。由于國際費雪效應成立的實質是實際利率平價的成立，因此單位根方法的主要目的就是檢驗兩國實際利差的平穩性。傳統的單位根方法(如ADF檢驗和PP檢驗)以及協整檢驗都假定:不管非均衡偏離的態勢如何，實際利率向均衡的調整過程是線性的，并且調整速度是一個常數。這種假定對于經濟中大量存在的非線性序列與調整速度非常數的變量而言并不適用，因而存在著很大的局限性。基于這種傳統單位根方法考察實際利率平價的代表性研究有 Wu ＆ Fountas［5］，Wu ＆ Chen［6］。

事實上，有許多因素導致了實際利差向長期均衡值調整的非線性。比如交易成本的存在(Obstfeld＆Taylor)［7］、資本不完全流動、實際匯率的非對稱性調整、央行對利率的管制(McMillan;Mark＆Moh)［8－9］、價格的剛性以及生產力的差別等等。此外，實際利差結構性突變點的存在也成為利差向均值非線性調整的重要原因(Cuestas＆Harrison)［10］。Perron［11］認為，如果忽略了結構性突變，那么拒絕序列存在單位的力度就會減弱，使結果更傾向于接受存在單位根的原假設，這也意味著在傳統線性模型下我們很容易得到國際費雪效應不成立的結論。

隨著計量技術的發展，近年來，非線性的單位根方法開始取代傳統的單位根檢驗，并取得了良好的實證效果。Arghyrou et al.［12］發現，在運用考慮了結構性突變點的單位根檢驗時，更容易得到實際利率平價成立的結論。Baharumshah et al.［13］運用非線性單位根方法對G－7國家和10個亞洲國家(地區)相對于美國和日本的利率平價進行了實證檢驗，發現除了臺灣、香港和菲律賓，其他國家的實際利率都遵循非線性的過程向實際利率平價調整。Su et al.［14］運用非線性門限單位根方法檢驗了東亞十個國家相對于中國的實際利率平價，發現有八個國家與中國的實際利率平價是成立的，說明來自中國的外部因素對東亞經濟體貨幣政策和財政政策的選擇及有效性影響較大。我國學者對于國際費雪效應的研究相對較少，并且實證方法相對傳統。俞穎［15］采用協整技術研究了東亞國家(地區)與美國、日本實際利率的長短期內在聯系，認為亞洲金融危機后，東亞經濟體對外金融一體化程度明顯提高，對內金融一體化則無顯著變化;并認為東亞經濟體的資本管制、合作深度及核心利率的缺失是影響東亞金融一體化的主要因素。

基于上述討論，本文采取一種對傳統單位根方法進行極大改進的非線性單位根方法——傅立葉函數的單位根方法，對東亞八個國家(地區)相對中國的國際費雪效應進行實證檢驗。Becker et al.、Christopoulos＆ León－Ledesma以及 Enders＆ Lee，通過彈性傅立葉變換(Flexible Fourier Transforms)將未知形式的突變模擬成一個平滑過程，從而發展出這種檢驗方法［16－18］。由于傅立葉單位根方法只需要對估計方程中的頻率進行識別，從而減少了待估參數，并確保無論突變發生的時間和形狀如何，這一檢驗都將有良好的檢驗力度。Chi－Wei Su［19］曾運用這一方法對中東歐七個國家的購買力平價進行了實證檢驗，發現保加利亞和羅馬利亞的匯率向長期均衡值的調整過程是非線性的。

本文運用LM統計量對國際費雪效應所預測的實際利差進行傅立葉單位根檢驗，我們允許序列在任何時間點出現任何形式的突變。基于有限的文獻梳理，國內外尚無學者運用傅立葉函數的單根方法對東亞地區的國際費雪效應進行實證檢驗，而既有的對于國際費雪效應的研究也極少選取中國為基準國，本文將立足于中國視角，以中國為基準國檢驗東亞地區的國際費雪效應，從而考察中國對一區域的經濟輻射力和利率主導作用，這是本文的創新之處。

三、國際費雪效應的理論框架

在國際金融理論中，可以遵循兩種不同的思路將國際費雪效應推導出來，一種思路是在實際利率平價成立的前提條件下，將國內費雪效應擴展到兩國情況;另一種是將非拋補利率平價和相對購買力平價結合起來，得到一種綜合平價理論，即國際費雪效應。

(一)國內費雪效應擴展法

國內費雪效應最早是由Irving Fisher在1930年提出來的，Fisher認為，一國名義利率應該由兩個要素構成，一個是實際利率ρ，另一個是與利率同一時期內的預期通貨膨脹率πe，因此，其表達式為:

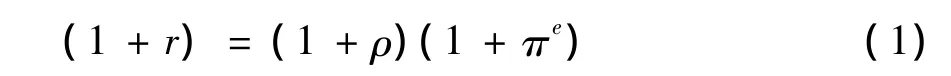
(1)式也經常被寫作其線性近似的形式，即利率等于實際利率加預期通貨膨脹率:

根據費雪的經濟理論，實際利率在一定時期內是穩定的。因此利率的波動主要是因為人們對通貨膨脹預期的修正。國際費雪效應的提出是受國內費雪效應的啟發，在兩國國內費雪效應分別成立的情況下，兩國利率的差異同預期通貨膨脹率之間的聯系如下:

國際費雪效應認為在理想狀態下，世界各國實際利率均相等，因此，名義利率的不同只是由于各國通貨膨脹預期不同造成的。國際費雪效應可以被寫成式(4):

或者利用線性近似，可以寫成:

(二)綜合平價理論法

首先，直接給出非拋補利率平價關系式:

利率平價理論認為，外幣兌本幣的預期貼水率等于外國利率與本國利率的差值，因而利率平價關系式可以變換為:

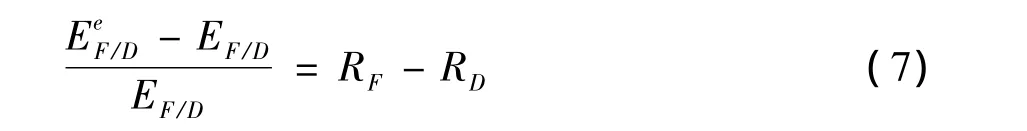
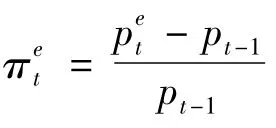
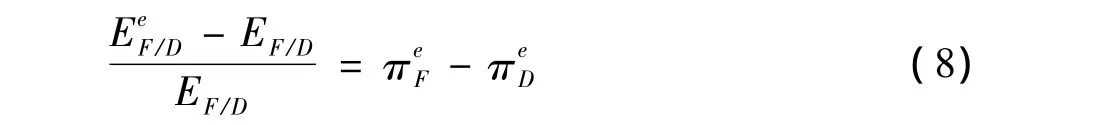
最后，將利率平價關系式(7)和購買力平價關系式(8)聯立，可以得到:

可以發現，上述兩種思路所得到的表達式一樣，上式表明，在其他條件不變的情況下，若一國的預期通貨膨脹率上升，最終會導致該國國內利率的同比例變動。

四、計量模型與方法

在前文我們得到了國際費雪效應的表達式，其中預期的通貨膨脹率在實踐中我們無法觀察，但根據適應性預期理論，我們可以用通貨膨脹率的歷史值代替預期值。所以國際費雪效應轉化為:

即兩國的名義利率之差等于兩國通貨膨脹率之差，這個等式的成立取決于兩國利率市場、匯率市場的開放程度以及資本的自由流動程度，如果兩國金融市場完全開放，資本流動不受限制，則這一等式嚴格成立。然而，這些假設在現實中難以成立，這意味著由于資本管制和金融市場的封閉性會產生實際利差λt，λt可以看作兩國金融市場的系統風險溢價，如果這一風險溢價收斂到一個不為零的常數，意味著非嚴格的費雪效應成立。風險溢價λt可以表示為:

這個等式說明，如果國外利率比國際費雪效應預測的高，預示著實際利差超過了正常值，風險溢價大于因管制而產生的交易成本，預示著套利機會的出現，在沒有資本管制的情況下，資本會由國內流向國外，最終使得國外實際利率回歸到均衡值，從而費雪條件成立。如果風險溢價以較低的或者均值為0的遞減方差波動，則國外資本和基準國資本被認為是近似替代品，并被作為支持金融一體化的證據。當達到金融一體化時，風險溢價將消失，因此風險溢價可以作為衡量金融一體化的度量指標。根據國際費雪效應理論，風險溢價λt是一個平穩過程，因為存在利率、匯率和資本的管制以及非預期的經濟波動，將使λt隨時偏離常數值。這意味著我們可以將λt以VAR形式表示成如下等式:

我們可以將其轉化成:

如果國際費雪效應成立，我們需要檢驗λt中的單位根，即檢驗H0∶θ1=0和H1∶θ1＜ 0，我們允許θ0≠0，因為不同的國家有不同的風險溢價。為了確定東亞地區是否存在國際費雪效應，本文依據Enders＆Lee［18］提出的帶有傅立葉函數的單位根檢驗，利用彈性傅立葉變換(Gallant)［20］來控制突變點未知的特征。這種傅立葉函數的一個優點在于，它僅用數量很少的頻率分量(frequency components)就可以描述一個或者更多結構突變點的本質特征。

Enders＆Lee［18］在傅立葉單位根方法中運用了LM檢驗，在此之前，Pascalau［21］曾指出，LM 方法比ADF方法具有更強的檢驗力度。沿用上述方法，我們考慮如下數據生成過程:

選擇［sin(2πkt/T)，cos(2πkt/T)］，是因為傅立葉表達式可以將絕對可積函數近似到任意想要的精度。其中 k表示頻率，γ = ［γ1，γ2］′測度頻率分量的振幅和位移。方程(14)的一個優點在于，如果令γ1=γ2=0，就會出現標準線性回歸的特殊情況。而且如果存在結構突變點，就至少會有一個頻率分量。在這種情況下，如果可以拒絕原假設γ1=γ2=0，此序列就必須存在一個非線性的組成部分。利用方程(14)的這一性質，使得在應對未知形式突變點時，Enders＆ Lee的方法比標準的Bai＆ Perron［22］方法更強有力。在原假設β=1、備擇假設β＜1的條件下，利用LM方法，對下面回歸方程做一階差分估計:

如果λt有單位根，則θ=0，LM檢驗統計量(記作τLM)是針對原假設θ=0的t統計量。假設新息過程滿足Phillips＆Perron［23］的序列相關和異方差假設。在方程(18)中添加滯后值 Δ～St-j，j=1，2，…p，可以除去殘余的序列相關性。Enders＆Lee［18］得出了τLM統計的漸進分布性質，并證明它僅取決于k的取值，與數據生成過程中的其他參數無關。方程(18)中的頻率可以通過最小化殘差平方和的方法得出。然而，他們的蒙特卡洛實驗證明最優頻率為1或2，因為更多的頻率會減弱檢驗力度［18］。

五、實證分析

本文采用2000年1月到2012年11月的月度數據，運用傅立葉單位根方法，檢驗東亞八個國家(地區)與中國的國際費雪效應是否成立。本文選取的東亞國家(地區)分別是印度尼西亞、馬來西亞、新加坡、泰國、日本、韓國、中國臺灣、中國香港，基準國是中國。名義利率本文主要采用了貨幣市場利率，其中除中國名義利率為銀行間7天內同業拆借利率，臺灣為金融業拆款利率外，其他七個經濟體均為貨幣市場利率。中國和臺灣的名義利率來自同花順數據庫，其他七個經濟體名義利率來自wind數據庫。通貨膨脹率是根據各經濟體的定基CPI計算得來，反映了樣本期間各月物價相對于基期2000年1月的變動水平。定基CPI指數除香港和新加坡來自wind數據庫外，其他經濟體來自同花順數據庫。

傅立葉單位根方法的步驟如下:第一步，運用格點搜索法尋找最優頻率，格點搜索法可以在對序列存在未知特征突變點的情況下尋找最優解。第二步，令 K 依次取 1、2、3、4、5，分別估計方程(16)，Enders＆Lee［18］認為，單一頻率即可匹配突變點的各種形態。

表1中第二列顯示了使殘差平方和最小的頻率值，第一列是相應的最小化殘差平方和。結果表明，除了馬來西亞的頻率為3外，其他經濟體單一頻率擬合效果最好。非線性檢驗的F統計量列示在第四列，八個經濟體的F統計量都達到1%的顯著性水平，有力拒絕了序列為線性形式的原假設，表明sine函數和cosine函數應該包含在估計的模型之中，如圖1所示，實際利差向均衡值的調整過程是非線性的，并且調整速度不為常數。遵循Perron的方法，本文在10%的顯著性水平下，采用t統計量選擇滯后階數。表1中第五列顯示了為排除殘差項序列相關所需要的滯后階數。最后一列報告了采用估計的頻率參數進行傅立葉單位根檢驗的結果。

表1 傅立葉函數的單位方法根檢驗結果

結果顯示，除了馬來西亞和日本，在1%的顯著性水平下我們拒絕了其他六個經濟體存在單位根的原假設。拒絕日本存在單位根所需要的最小顯著性水平為5.08%，說明日本與中國大陸的國際費雪效應較弱。馬來西亞的t統計量非常小，以至于在20%的顯著性水平下，都無法拒絕存在單位根的原假設，說明馬來西亞與中國大陸的國際費雪效應不存在。在圖1中,我們繪制了各國(地區)相對于中國的實際利率差異走勢圖，以及包含傅立葉函數的非線性擬合值。由圖1不難發現，表一中結果顯著的六個國家(地區),其相對于中國的實際利率差異被擬合的較好，而馬來西亞即使用了頻率為3的非線性擬合，其效果也較差。實證結果表明，除了日本和馬來西亞，東亞其他六個國家(地區)與中國的國際費雪效應都成立，我們認為，這六個國家(地區)與中國存在國際費雪效應的共同原因有三個:第一，區域內資本管制的不斷放松。面對亞洲金融危機,各國(地區)雖然都采取短暫資本管制措施，但從2001年后資本管制開始不斷放松，這極大地促進了各國(地區)資本的自由流動，這可以從東亞地區股票市場和債券市場一體化程度得以佐證，張茜等［24］通過實證研究發現，東亞地區持有區域內股票規模占持有外國股票總額比例從2001年的20.8% 上升至2009年的34.3%，而其所持有的歐美的份額則從41.6%下降至25.4%。這說明東亞股票市場無論是區域內還是區域外其一體化程度均在不斷深化，但區域內的一體化增速遠高于區域外的。另一方面，東亞地區的債券市場一體化程度也在加強，且區域內一體化速度遠大于區域外的。第二，東亞各國(地區)的貿易開放度不斷增強。鄭海青和王世文［25］通過對東亞地區金融一體化因素進行實證研究發現，貿易開放程度提高顯著促進了這一區域金融市場一體化;并且經常賬戶盈余使一國凈國際投資頭寸上升，促進了金融一體化。第三，區域內宏觀經濟聯動性增強,這主要體現為各國(地區)消費聯動性的增強。鄭海青和王世文［25］對東亞地區金融一體化的實證研究發現，一國消費比重提高1%，相應的金融一體化水平就增加3.026%，說明消費聯動性是東亞地區金融一體化的重要原因。

然而，東亞金融一體化進程中還面臨著一定的挑戰。首先，日本與中國國際費雪效應較弱，出現這一情況的原因有三:一是日本的貿易結構和國內市場緩慢的開放速度使其與東亞其他國家的貿易依存關系大幅減弱。二是其國內金融市場固有的封閉性，使其遠沒有中國大陸對外資的吸引力，因此難以成為東亞各經濟體資本流動的聚集地。三是日本為了應對亞洲金融危機而對日元采取的競爭性貶值，相當于對匯率實施了管制，使日元作為東亞地區核心貨幣的地位不斷下降，這與日本長期的經濟低迷狀況是相輔相成的。由上述分析不難發現，日本金融市場固有的封閉性及嚴格的管制政策，使其與中國宏觀經濟基本面的聯動性大大降低，這從根本上阻礙了其與中國國際費雪效應的成立，這與俞穎［15］通過協整檢驗得到的結論是基本一致的。

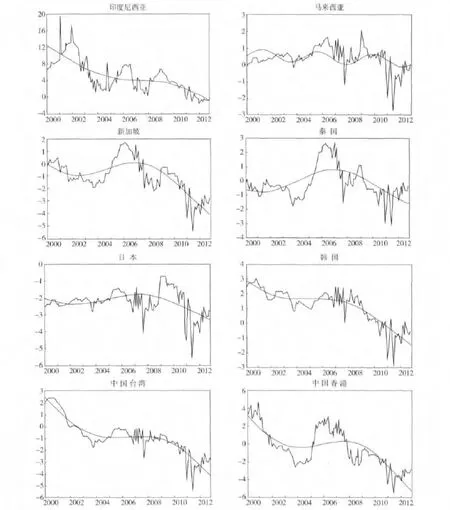
圖1 東亞各國(地區)相對于中國實際利差的變動

馬來西亞與中國完全不存在費雪效應，本文認為主要有原因有四:第一，為了應對亞洲金融危機，馬來西亞所采取的嚴格而激進的資本管制措施對經濟造成了長期而深遠的負面影響，大大降低了其與中國經濟的聯動性。第二，馬來西亞收入分配結構失衡導致社會有效消費需求不足，造成國內市場狹小。第三，馬來西亞體制改革滯后和腐敗問題，使得主要經濟活動和關鍵經濟領域都被官聯機構(GLCs)壟斷，導致外資的潛在投資空間變得非常狹窄。第四，經濟結構不合理，導致馬來西亞的經濟體系在受到經濟危機沖擊時變得十分脆弱。馬來西亞成為受2007年世界金融危機沖擊最大的東亞國家之一，并在2009年爆發了外資出逃危機，這一危機使馬來西亞出現了嚴重的通貨緊縮，如圖2所示。上述因素使得馬來西亞與中國經濟的關聯程度大大降低，圖2表明，馬來西亞在2005年與2009年都出現了異常的通貨緊縮，而這種結構性變動并未出現在中國，這印證了前文的分析，即兩國的費雪效應不成立，極可能來自兩國通脹差異的擴大;另外，不難發現馬來西亞的利率波動較小，這暗示著馬來西利率市場化程度不夠，這同樣會造成兩國利率差異偏離長期均衡值。

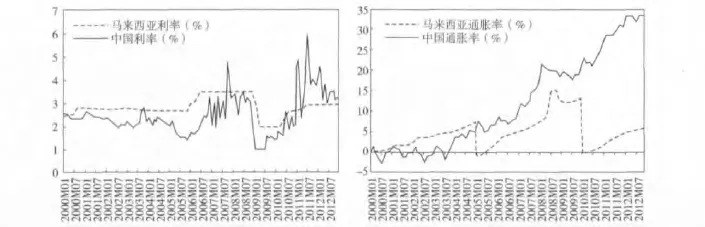
圖2 中國與馬來西亞名義利率和通貨膨脹率

由上述分析可以發現，與中國國際費雪效應成立的國家滿足資本賬戶開放度高、資本自由流動、雙邊經貿關系密切等共同條件，而與中國國際費雪效應不成立的國家由于自身特殊原因造成對上述條件或多或少的違背。

六、結論與政策啟示

(一)結論

本文運用傅立葉單位根方法，對東亞八個國家(地區)相對于中國的國際費雪效應進行了實證檢驗。結果顯示，印度尼西亞、新加坡、泰國、日本、韓國、臺灣、香港六個經濟體與中國大陸存在顯著的費雪效應，日本與中國大陸的費雪效應較弱，馬來西亞與中國大陸的國際費雪效應不存在。與以往的研究不同，本文結果顯示，上述國家(地區)相對于中國的實際利差向長期均衡值的調整是非線性的，并且調整速度不是常數。這一方面說明，東亞大部分國家(經濟體)與我國經濟發展趨同，金融一體化趨勢明顯;另一方面，說明我國實際利率水平已逐漸成為東亞地區的驅動利率，來自我國的外部因素對其他東亞國家(地區)經濟政策的制定和實施具有重要影響。但同時，東西地區金融一體化進程依然面臨著挑戰，這主要來自于少數國家(地區)所存在的資本的管制，以及國內特殊的政治、經濟問題，這為我國制定國際化戰略提供了經驗啟示。

(二)政策啟示

隨著東亞地區經濟、金融一體化步伐加快，中國需要抓住金融自由化改革的契機，不斷深化市場體制改革，加快資本賬戶的開放速度，推進利率市場化進程，促進資本的自由流動，加強區域內經貿合作，從而進一步降低其他國家與我國的金融市場主體的交易成本，增強我國金融市場在東亞地區的輻射力，使我國成為東亞地區金融一體化的主導國。同時，從日本和馬來西亞的經驗中得出，我國一方面要在日元作為東亞地區核心貨幣的地位不斷下降的情況下，不斷放松對匯率的管制，加快人民幣區域化和國際化進程，從而真正確立人民幣在東亞地區的核心貨幣地位。另一方面，要不斷擴大國內需求和國內市場，使國民經濟能夠持續、健康的增長，同時要妥善處理影響我國一體化進程的收入分配結構不合理等問題。

［1］ Frenkel J A.Monetary approach to exchange rate:doctrinal aspects of empirical evidence［J］.Scandinavian Journal of Economics，1976，78:200–224.

［2］ Mussa M.The exchange rate，balance of payment，and monetary and fiscal policy under a regime of controlled floating［J］.Scandinavian Journal of Economic，1976，78:229-248.

［3］ Mark N C.Some evidence on the international inequality of real interest-rates［J］.Journal of International Money and Finance，1985，4:189-208.

［4］ Goldberg L G，Lothian J R，Okunev J.Has international financial integration increased?［J］.Open Economies Review，2002，14:299-317.

［5］ Wu J L，Fountas S.Real interest rate parity under regime shifts and implications for monetary policy［J］.Manchester School，2000，68:685-700.

［6］ Wu J L，Chen S L.A re-examination of real interest rate parity［J］.Canadian Journal of Economics，1998，31:837-851.

［7］ Obstfeld M，Taylor A M.Nonlinear aspects of goodsmarket arbitrage and adjustment:Heckscher′s commodity points revisited［J］.Journal of the Japanese and International Economies，1997，11:441-479.

［8］ McMillan D G.Non-linear error correction:evidence for UK interest rates ［J］.Manchester School，2004，72:626-640.

［9］ Mark N C，Moh Y K.The real exchange rate and real interest differentials:the role of nonlinearities［J］.International Journal of Finance and Economics，2005，10:323-335.

［10］ Cuestas J C，Harrison B.Further evidence on the real interest rate parity hypothesis in central and eastern European countries:unit roots and nonlinearities［J］.E-merging Markets Finance and Trade，2010，46:22-39.

［11］ Perron P.The great crash，the oil price shock and the unit root hypothesis ［J］.Econometrica，1989，57:1361-1401.

［12］ Arghyrou M G，Gregoriou A，Kontonikas A.Do real interest rates converge?Evidence from the European Union［J］.Journal of International Financial Markets，2009，19:447-460.

［13］ Baharumshah A Z，Venus K S L，Haw C T.The real interest rate differential:international evidence based on non-linear unit root tests［J］.Bulletin of Economic Research，2009，61:83-94.

［14］ Su C W，Shen P L，Chang H L.Real interest rate parity in east Asian countries based on China with nonlinear threshold unit root test［J］.Applied Economics Letters，2012，19:1531-1536.

［15］ 俞穎.東亞金融一體化研究——基于實際利率平價理論的分析與探討［J］.山西財經大學學報，2009(1):93-99.

［16］ Becker R，Enders W，Lee J.A stationarity test in the presence of an unknown number of smooth breaks［J］.Journal of Time Series Analysis，2006，17:381-409.

［17］ Christopoulos D K，León-Ledesma M A.Revisiting the real wages-unemployment relationship new results from non-linear models［J］.Bulletin of Economic Research，2010，62:79-96.

［18］ Enders W，Lee J.A unit root test using a Fourier series to approximate smooth breaks［J］.Oxford Bulletin of E-conomics and Statistics，2012，74:574-599.

［19］ Su C W.Flexible Fourier stationary test in purchasing power parity for central and eastern European countries［J］.Ekonomicky Casopis，2012，1:19-31.

［20］ Gallant R.On the basis in flexible functional form and an essentially unbiased form:the flexible Fourier form［J］.Journal of Econometrics，1981，15:211-253.

［21］ Pascalau R.Unit root tests with smooth breaks:an application to the Nelson-Plosser data set［J］.Applied Economics Letters，2010，17:565-570.

［22］ Bai J，Perron P.Estimating and testing linear models with multiple structural changes ［J］.Econometrica，1998，66:47-78.

［23］ Phillips P C B，Perron P.Testing for a unit root in time series regression ［J］.Biometrica，1988，75:335-346.

［24］ 張茜，楊攻研，劉洪鐘.東亞金融一體化現狀及挑戰——基于細分市場的研究［J］.亞太經濟，2012(5):37-42.

［25］ 鄭海青，王世文.東亞金融一體化決定因素的實證分析［J］.山西財經大學學報，2007(12):107-112.