通過小信號環(huán)路估計DC-DC開關變換器的大信號穩(wěn)定區(qū)域預測

劉宿城 周雒維 盧偉國 畢 凱

（重慶大學輸配電裝備及系統(tǒng)安全與新技術國家重點實驗室 重慶 400044）

1 引言

開關功率變換系統(tǒng)本質上是一類特殊的強非線性系統(tǒng)，從數(shù)學描述上表現(xiàn)為右邊非連續(xù)的分段化線性狀態(tài)方程[1]。當開關頻率遠高于系統(tǒng)的截止頻率和擾動頻率時，可通過狀態(tài)平均化的思想忽略高頻分量，建立系統(tǒng)的低頻小信號動態(tài)模型，借助線性系統(tǒng)理論工具（Bode圖，Nyquist曲線，根軌跡等），以此進行控制系統(tǒng)的分析與綜合[2]。然而，小信號模型雖能準確描述系統(tǒng)在小信號低頻擾動下的響應特性，卻無法準確反應系統(tǒng)的大信號（如起動過程、負載突變等）行為，甚至小信號穩(wěn)定設計的變換器在大信號擾動下會出現(xiàn)失穩(wěn)現(xiàn)象[3,4]。

對于一個閉環(huán)反饋控制系統(tǒng)來說，穩(wěn)定性是其基本要求。大信號穩(wěn)定性研究的是系統(tǒng)在大擾動情況下（如電壓突變、負載切換、控制器飽和甚至系統(tǒng)結構的變化）的收斂行為。現(xiàn)有研究大信號穩(wěn)定性最簡單也最常見的方法是時域仿真法，其機理是對描述變換器動態(tài)行為的非線性微分方程進行數(shù)值求解。由于電力電子系統(tǒng)中負荷和開關過程的時間常數(shù)相差非常大，造成這種病態(tài)系統(tǒng)的計算時間較長。雖然通過先進的建模手段和仿真算法可以縮短仿真時間[5-7]，但是時域仿真得到的結果物理意義不清晰，對設計的指導作用不夠明顯。另一方面，解析法中具有代表性的有雅可比矩陣求解法[8]、虛擬平衡點法[3]以及Lyapunov法[11]等。雅可比矩陣求解法與虛擬平衡點法均從系統(tǒng)的大信號狀態(tài)方程出發(fā)，以反饋系數(shù)組成占空比的約束表達式，然后通過求解系統(tǒng)的雅可比矩陣或是直接求解狀態(tài)方程，以此確定系統(tǒng)參數(shù)在大信號變化下的穩(wěn)定邊界。而對穩(wěn)定區(qū)域與控制參數(shù)的解析分析方面，通常將控制器簡化為純比例結構，側重于反饋增益的取值對穩(wěn)定區(qū)域的影響[3,9,10]。與前述兩種解析法不同，Lyapunov穩(wěn)定性理論是衡量動態(tài)系統(tǒng)穩(wěn)定性的一般性基礎理論，目前已被廣泛用于電力電子系統(tǒng)的穩(wěn)定性分析與控制器設計[12-16]。基于Lyapunov直接法，根據(jù)系統(tǒng)的本質特性構建合適的Lyapunov能量泛函，可以估計系統(tǒng)平衡點的收斂區(qū)域。由于Lyapunov函數(shù)的非唯一性，不同 Lyapunov函數(shù)得到的收斂區(qū)域也會不同[17]，針對特定系統(tǒng)建立最優(yōu)Lyapunov函數(shù)尚存挑戰(zhàn)。

本文提出從 DC-DC開關變換器的大信號擾動模型出發(fā)，借助范數(shù)不等式推導出變換器的充分穩(wěn)定條件，建立起小信號環(huán)路增益與大信號穩(wěn)定性之間的關系，并以此估計閉環(huán)系統(tǒng)的穩(wěn)定區(qū)域。文中以Boost變換器為例，說明該方法的推導過程，并以仿真和實驗結果驗證方法的有效性。

2 Boost變換器的大信號擾動模型

圖1為典型平均電流模式控制的Boost變換器原理框圖。假設Boost變換器工作在電感電流連續(xù)導電模式，即開關功率管S與二極管VD互補工作，變換器可描述為如下分段線性狀態(tài)方程組

式中，x為狀態(tài)向量；A1,2、B1,2為系數(shù)矩陣；Ts為開關周期；d則代表占空比。

圖1 典型Boost變換器Fig.1 Typical Boost converter

根據(jù)線性紋波近似法[2]，上述分段線性方程組可近似描述為開關周期平均意義下的連續(xù)狀態(tài)方程

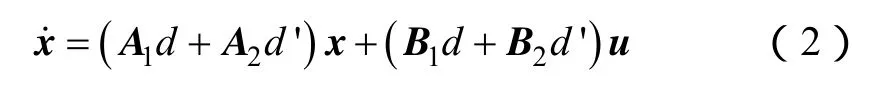
將狀態(tài)變量和控制變量看作為穩(wěn)態(tài)值與擾動的疊加，即

式中，X和?x分別為狀態(tài)變量的穩(wěn)態(tài)量和擾動量；D和?d分別為占空比變量的穩(wěn)態(tài)量和擾動量。

將式（3）代入式（2），整理得到

式中

注意到，式（4）中方程式右邊由于存在控制輸入（占空比）和狀態(tài)變量的乘積，因此描述的是典型的雙線性系統(tǒng)。

代入圖1中的電路元器件和變量符號，可得到如下Boost變換器的狀態(tài)方程

上述方程即對應圖2所示的Boost變換器在大信號擾動下的電路模型。至此，在建模的過程中并未做小信號近似，因此該模型適用于大信號分析。值得一提的是，若忽略其中的雙線性項，則可得到傳統(tǒng)的小信號線性模型。

圖2 Boost變換器的大信號擾動電路模型Fig.2 Large-signal perturbed circuit model of the Boost converter

為驗證該模型的正確性，進行了電路仿真實驗，其中 Boost電路的主要參數(shù)為：L=120μH，C=300μF，R=12?，RL=250m?，Vg=12V，VO=24V；仿真結果如圖3所示，若忽略開關紋波分量，所建大信號模型與實際電路的瞬態(tài)響應基本一致。

圖3 大信號模型驗證結果Fig.3 Verification of the large-signal model

3 環(huán)路增益設計

在進行大信號分析之前，有必要先設計 Boost變換器的環(huán)路增益以確保系統(tǒng)的小信號控制性能。根據(jù)圖1，可推導平均電流模式控制 Boost變換器的控制框圖如圖4所示。平均電流模式為雙環(huán)控制結構：內(nèi)環(huán)為電流環(huán)（控制器為Fi），起到對參考電流快速跟蹤的作用；外環(huán)為電壓環(huán)（控制器為Fv），其作用是為電流內(nèi)環(huán)提供參考信號以控制輸出期望電壓值。雙環(huán)控制結構相比單環(huán)控制具有更優(yōu)越的動態(tài)性能，因此被廣泛應用于高功率因數(shù)整流器以及高動態(tài)升壓調(diào)節(jié)器中。

圖4 平均電流控制Boost變換器的控制框圖Fig.4 Control block diagram for the average-current mode controlled Boost converter

根據(jù)圖4中控制結構框圖，將電流內(nèi)環(huán)等效為電壓外環(huán)的一個獨立子環(huán)節(jié)，那么等效后的電壓外環(huán)路增益為

式中，電流環(huán)路增益 Ti(s)=RiFi(s)FmGid(s)，Ri、Fi(s)、Fm和 Gid(s)分別為電流采樣增益、電流控制器、PWM調(diào)制器增益和占空比到電感電流的傳遞函數(shù)；電壓環(huán)路增益Tv(s)=βvFv(s)FmFi(s)Gvd(s)，其中βv、Fv(s)和Gvd(s)分別為電壓采樣增益、電壓控制器和控制到輸出電壓的傳遞函數(shù)。

這里，電流環(huán)和電壓環(huán)的控制器均采用II型補償器，即單零點-雙極點補償網(wǎng)絡，其傳遞函數(shù)分別為

假設Boost變換器的額定功率為50W，其主電路參數(shù)見下表，那么相應電流補償器和電壓補償器的設計參數(shù)分別為：ωi=9 627，ωiz=2 273，ωip=502 300，Ri=0.11，F(xiàn)m=1/3.2；βv=0.208，ωv=5 895,ωvz=377，ωvp=256 800。補償后的等效電壓外環(huán)路增益如圖5所示，其中圖5a為仿真計算結果，圖5b為借助頻率響應分析儀（型號為Model 3120）進行電路實驗測得的結果，二者基本吻合。從圖中可以看出，等效電壓環(huán)路增益 To(s)的截止頻率為 1.2kHz，相位裕度和增益裕度分別為 80°和 7.5dB。另外，圖5也表明，雙環(huán)控制下的Boost變換器在低頻段內(nèi)的頻域響應近似表現(xiàn)為一階系統(tǒng)行為。

表 Boost變換器的主電路參數(shù)Tab.Parameters for the Boost power stage

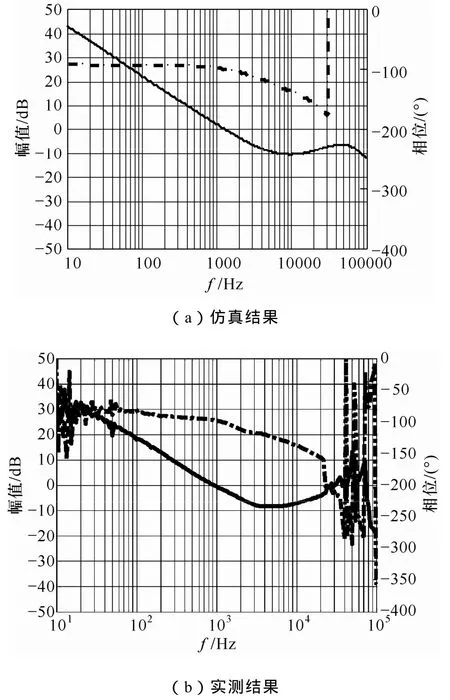
圖5 補償后的等效外環(huán)路增益Fig.5 Compensated loop gains for the equivalent outer voltage loop

4 穩(wěn)定區(qū)域估計

根據(jù)前述推導，Boost變換器的大信號擾動模型為雙線性系統(tǒng)形式，而且傳遞函數(shù)模型中存在右半平面零點，使得基于小信號設計的 Boost變換器在大信號擾動下易于出現(xiàn)不穩(wěn)定行為。本節(jié)將根據(jù)范數(shù)不等式確定變換器的充分穩(wěn)定區(qū)域，并以此揭示小信號環(huán)路設計對穩(wěn)定區(qū)域的影響。

由 Boost變換器的控制結構框圖（見圖3）可知，控制占空比有如下關系

式中，dz為輸入擾動，代表電壓外環(huán)的初始狀態(tài)。

同時，根據(jù)式（5）可得出

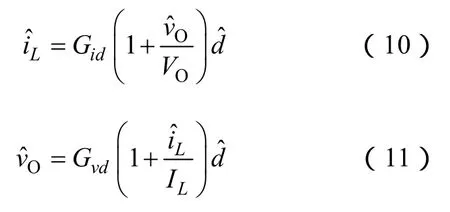
將式（10）與式（11）代入式（9）得到

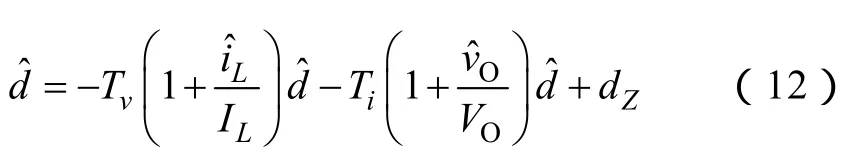
將式（12）整理為

對式（13）應用范數(shù)三角不等式，然后整理得到如下關系

根據(jù)上式，閉環(huán)控制 Boost變換器達到穩(wěn)定的充分條件是要求占空比表達式的分母為大于零的正數(shù)，即滿足不等式

式（15）表明了 Boost變換器控制系統(tǒng)大信號穩(wěn)定的充分條件，可用來估計系統(tǒng)的大信號穩(wěn)定區(qū)域。

根據(jù)上文中提供的系統(tǒng)參數(shù)，可以算出|Tv/(1+Ti+Tv)|=1.08，|Ti/(1+Ti+Tv)|=2.16，結合式（15）可以畫出Boost變換器的充分穩(wěn)定區(qū)域如圖6所示，圖中陰影部分表示狀態(tài)變量能達到穩(wěn)定狀態(tài)時所能允許的最大擾動范圍。另外，可以推測，不同的環(huán)路增益會得到不同的穩(wěn)定區(qū)域。

將環(huán)路增益作為變量，根據(jù)圖6結果可計算出不同環(huán)路增益下的穩(wěn)定區(qū)域面積S為

圖6 閉環(huán)控制Boost變換器的預測穩(wěn)定區(qū)域Fig.6 Predicted stability region for the closed-loop controlled Boost converter

由式（16）可進一步得到如下關系

根據(jù)式（17），環(huán)路增益的取值對面積S和擴展面積S′的影響均為正定單調(diào)，因此可用擴展面積S′近似分析電壓環(huán)和電流環(huán)增益分別對實際穩(wěn)定區(qū)域S的影響。圖7即為擴展穩(wěn)定區(qū)域面積S′與環(huán)路增益的關系。

圖7 穩(wěn)定區(qū)域與環(huán)路增益的關系Fig.7 Relationship between the stability region and the loop gains

可以看出，在電流環(huán)增益（電壓環(huán)增益）較小的位置，隨著電壓環(huán)增益（電流環(huán)增益）的增加，穩(wěn)定區(qū)域也隨之擴大；而在電流環(huán)增益與電壓環(huán)增益所占比例相當時（圖中中間區(qū)域），穩(wěn)定區(qū)域最小，穩(wěn)定性也最差。因此，在小信號設計的基礎之上，可借助此方法估計控制器的大信號穩(wěn)定區(qū)域，以修正控制器參數(shù)對系統(tǒng)進行穩(wěn)定性再設計，而不需要改變控制器結構。

5 實驗驗證

為了驗證前述分析的有效性，根據(jù)設計參數(shù)搭建了 Boost變換器實驗樣機，其中主電路參數(shù)取值與上文表中所列參數(shù)一致，控制電路參數(shù)也與第 3節(jié)中仿真取值基本一致。圖8為Boost變換器在額定條件下的穩(wěn)態(tài)實驗波形，其中 vGS為開關驅動脈沖，開關頻率為 110 kHz，vg與 vO分別為輸入電壓與輸出電壓，iL為電感電流，其額定值為4.5A。

圖8 Boost電路的穩(wěn)態(tài)波形Fig.8 Steady state waveforms for the Boost converter

根據(jù)第4節(jié)中穩(wěn)定區(qū)域估計結果，選取圖6中穩(wěn)定區(qū)域內(nèi)、外兩點Poutr與Pinr作為測試點對Boost變換器進行了動態(tài)電路實驗，其中 Pinr點處狀態(tài)變量即電容電壓與電感電流的取值為（20V,6.8A），而Poutr點處狀態(tài)變量的取值為（20V,7.8A）。圖9a即為Boost變換器在20V輸出時，電感電流從額定值4.5～6.8A（點Pinr處的電感電流值）脈沖切換下的時域動態(tài)響應波形，圖9b則為圖9a中虛線框內(nèi)波形的局部放大效果。從圖中可以看出，在此種情況下，Boost變換器能始終通過過渡過程達到期望的單周期穩(wěn)定狀態(tài)。

圖9 電感電流從額定值至Pinr處的電流切換下的動態(tài)波形Fig.9 Dynamic waveforms for the inductive current step from the nominal value to that of Pinr

圖10a為Boost變換器在20V輸出時，電感電流從額定值 4.5～7.8A（點 Poutr處的電感電流值）脈沖切換下的時域動態(tài)響應波形，圖10b同樣為圖10a中虛線框內(nèi)波形的局部放大效果。可以看出，此種狀態(tài)下，Boost變換器從額定電感電流至 Poutr處電感電流跳變后無法達到單周期穩(wěn)態(tài)，開關驅動脈沖呈現(xiàn)多開關周期狀態(tài)，此時的電感電流出現(xiàn)較大幅度振蕩，電流紋波值為穩(wěn)定狀態(tài)時的4倍左右，同樣也導致輸出電壓紋波量的增加。電路實驗結果與前述理論分析基本一致，較好地驗證了穩(wěn)定區(qū)域估計的有效性。

圖10 從電感電流額定值至Poutr處的電流切換下的動態(tài)波形Fig.10 Dynamic waveforms for the inductive current step from the nominal value to that of Poutr

6 結論

本文以平均電流控制 Boost變換器為研究對象，提出一種估計閉環(huán)控制系統(tǒng)的大信號穩(wěn)定區(qū)域的解析方法。通過推導占空比的表達式，借助范數(shù)三角不等式，可得出閉環(huán)控制 Boost變換器在大信號擾動下的充分穩(wěn)定條件。電路實驗結果驗證了該方法的有效性。

考慮到開關功率變換器的主流分析方法與設計仍然是基于系統(tǒng)靜態(tài)工作點上取小信號模型的思路，本文中得到的結果可用于開關功率變換器的穩(wěn)定性再設計。通過解析分析小信號環(huán)路對大信號穩(wěn)定性的影響，以期達到小信號與大信號的綜合設計。后續(xù)研究工作將細化控制器各參數(shù)對穩(wěn)定區(qū)域的影響，并以動態(tài)性能與穩(wěn)定性的最佳折中為設計導向，對所提方法進行優(yōu)化。

[1] 王剛,馬偉明,付立軍,等.周期分段線性系統(tǒng)穩(wěn)定性理論[J].電工技術學報,2010,25(12): 84-91.Wang Gang,Ma Weiming,Fu Lijun,et al.Stability theory of periodic piecewise linear system[J].Transactions of China Electrotechnical Society,2010,25(12): 84-91.

[2] Middlebrook R D,Cuk S.A general unified approach to modeling switching-converter power stages[J].International Journal of Electronics,1977,42(6):521-550.

[3] Erickson R W,Cuk S,Middlebrook R D.Large-signal modelling and analysis of switching regulators[C].Proc.Annual Power Electronics Specialists Conference,1982.

[4] 張波.電力電子變換器非線性混沌現(xiàn)象及其應用研究[J].電工技術學報,2005,20(12): 1-12.Zhang Bo.Study of nonlinear chaotic phenomena of power converters and their applications[J].Transactions of China Electrotechnical Society,2005,20(12): 1-12.

[5] Guinjoan F,Calvente J,Poveda A,et al.Large-signal modeling and simulation of switching DC-DC converters[J].IEEE Transactions on Power Electronics,1997,12(3): 485-494.

[6] Sun J,Grotstollen H.Symbolic analysis methods for averaged modeling of switching power converters[J].IEEE Transactions on Power Electronics,1997,12(3):537-546.

[7] Lineykin S,Ben-Yaakov S.Unified SPICE compatible model for large and small-signal envelope simulation of linear circuits excited by modulated signals[J].IEEE Transactions on Industrial Electronics,2006,53(3): 745-751.

[8] Tan F D,Ramshaw R S.Instabilities of a boost converter system under large parameter variations[J].IEEE Transactions on Power Electronics,1989,4(4):442-449.

[9] Olalla C,Queinnec I,Leyva R,et al.Optimal statefeedback control of bilinear DC-DC converters with guaranteed regions of stability[J].IEEE Transactions on Industrial Electronics,2011,59(10): 3868-3880.

[10] Chung H,Ioinovici A.Design of feedback gain vector of two-state basic PWM multifeedback regulators for large-signal stability[J].IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications,1997,44(8): 676-683.

[11] Sanders S R,Verghese G C.Lyapunov-based control for switched power converters[J].IEEE Transactions on Power Electronics,1992,7(1): 17-24.

[12] Chen F,Cai X S.Design of feedback control laws for switching regulators based on the bilinear large signal model[J].IEEE Transactions on Power Electronics,1990,5(2): 236-240.

[13] 張涌萍,張波,陳斌,等.基于雙線性系統(tǒng)理論的Boost DC-DC變換器新型控制策略[J].電工技術學報,2006,21(7): 109-114.Zhang Yongping,Zhang Bo,Chen Bin,et al.A novel control law of boost DC-DC converter based on bilinear theory[J].Transactions of China Electrotechnical Society,2006,21(7): 109-114.

[14] Komurcugil H,Kukrer O.Lyapunov-based control strategy for power-factor preregulators[J].IEEE Transactions on Circuits and Systems I-Fundamental Theory and Applications,2003,50(9): 1226-1229.

[15] Mazumder S K,Acharya K.Multiple Lyapunov function based reaching condition analyses of switching power converters[C].2006 IEEE Power Electronics Specialists Conference,2006: 1160-1167.

[16] Hu T S.A nonlinear-system approach to analysis and design of power-electronic converters with saturation and bilinear terms[J].IEEE Transactions on Power Electronics,2011,26(2): 399-410.

[17] Sullivan C J,Sudhoff S D,Zivi E L,et al.Methods of optimal Lyapunov function generation with application to power electronic converters and systems[C].IEEE Electric Ship Technologies Symposium,2007: 267-274.