雙余度無刷直流電動機建模與熱損對比分析

徐健龍，李玉忍，皇甫宜耿

(西北工業大學，陜西西安710072)

0 引 言

隨著永磁無刷直流電機的技術成熟，其越來越多地被運用到航空、航天飛行器上，但它在運行過程中要產生大量的熱能。飛行器在高空稀薄的空氣中飛行，導致電機的散熱遠不如在地面理想，電機在運行過程中很可能因為散熱不佳而引起電機過熱損壞的情況［1］，因此，電機的熱損分析與研究有著重要意義。無刷直流電機采用冗余結構設計可以極大增加系統可靠性［2］，文獻［3］分析了隔槽與同槽嵌放在結構上雙余度無刷直流電機之間的差別。

本文在建立雙余度無刷直流電機數學模型的基礎上，分析了兩種不同電機繞組結構的雙余度無刷直流電機在正常工況與繞組斷路工況下的熱損情況，為兩種結構雙余度無刷直流電機的選擇提供了一定的理論依據。

1 雙余度無刷直流電機的數學模型

1.1 隔槽嵌放電機的數學模型

隔槽嵌放雙余度無刷直流電機有兩套三相集中繞組嵌放在定子槽內，繞組采用星型接法，兩套繞組之間互差30°電角度，三相橋電路由兩套獨立的功率電子器件實現驅動［4］，如圖1所示。

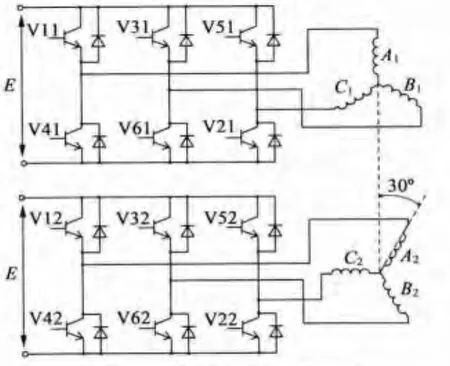
圖1 無刷直流電機結構

雙余度無刷直流電動機的兩套定子繞組在電路上是獨立的，但彼此間存在磁場耦合，兩套繞組間存在互感。余度1、余度2與雙余度合成磁場的關系如圖2所示。可以得到雙余度無刷直流電機的電壓平衡式:

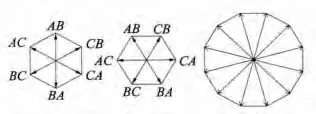
圖2 隔槽雙余度合成磁場關系

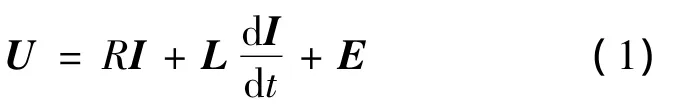
式中:U為定子相繞組電壓矩陣;I為定子相繞組電流矩陣;E為定子繞組電動勢矩陣;R為定子繞組相電阻;L為電感系數矩陣。其中:

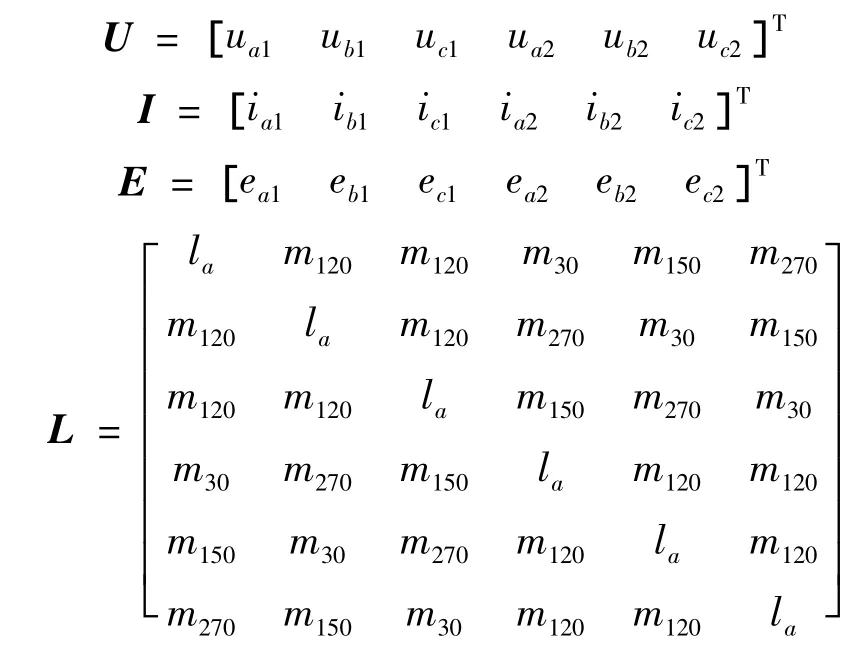
下標1表示第1余度的電流、電壓、電勢變量。下標2表示第2余度。參數la是相繞組電感，mθ(θ=30°、120°、150°、270°)是兩相繞組相差 θ電角度時的互感。由于兩個余度都是采用三相繞組星型接法，并且都沒有中線，則有下面等式:

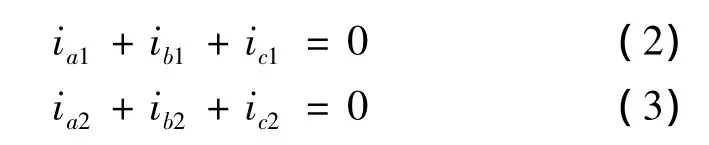
根據文獻［7］，當A相繞組與B相繞組重合時，互感M達到最大，M=L，當兩者互相垂直時，M=0。兩者相差120°即B相滯后A相(1+)90°時，兩者間互感是自感的。可見，繞組間互感與自感在空間與相互相位置角有如下線性關系:

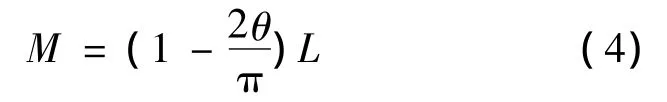
式中:θ為定、轉子軸線夾角;π為圓周率常數。于是可以得到L隔槽嵌放情況下簡化的電感系數矩陣L1。

1.2 同槽嵌放電機的數學模型

采用同槽嵌放結構時，定子槽內并列嵌放兩套三相集中繞組，繞組采用星型接法，兩套繞組之間沒有電角度差。余度1、余度2與雙余度合成磁場的關系如圖3所示。

圖3 同槽雙余度合成磁場關系

由于同槽嵌放情況下兩余度也是無中線三相星型結構，即式(2)和式(3)仍然成立，采用L*簡化至的方法，可以得到同槽嵌放結構簡化的電感系數矩陣L2。

2 雙余度無刷直流電機的MATLAB仿真

2.1 建立仿真模型

本文研究的是雙余度無刷直流電機繞組的發熱情況，所以搭建雙余度無刷直流電機速度、電流雙閉環模型。為了更好地分析電機的發熱情況，利用MATLAB中豐富的模塊庫，搭建了DR－BLDCM的伺服控制系統仿真模型［5－7］。

2.2 仿真結果

根據隔/同槽DR－BLDCM的特征數學模型，在MATLAB/Simulink軟件仿真環境下進行了電機的工作狀態仿真。電機實驗用參數:額定電壓Ue=160 V，額定轉矩TL=3.4 N·m，定子相繞組電阻 r=1.46 Ω，繞組自感 L=2 mH，轉動慣量 J=0.56 g·m2，額定轉速 ne=5 000 r/min，極對數 p=2，反電勢系數 Ke=0.018 5 V/(rad·s－1)。

兩種雙余度無刷直流電機分別帶額定負載3.4 N·m起動，得到電機輸出轉速n、電磁轉矩Te和A相電流波形Ia波形圖。隔槽嵌放DR－BLDCM波形如圖4～圖6所示，同槽嵌放DR－BLDCM波形如圖7～圖9所示。

從仿真波形可以發現，電機起動后，反電勢的幅值迅速增大(轉速很快升高)，使得相繞組電流幅值減小，結果顯示電磁轉矩也相應減小，隔/同槽雙余度電機都在40 ms的時間內進入穩定狀態;無刷直電機的換向引起了電磁轉矩的脈動;余度1每相的反電勢和相電流與余度2的完全相同，這是因為同槽嵌放DR－BLDCM兩個余度的相繞組不存在位置角偏差，但電磁轉矩及轉速脈動比隔槽嵌放的雙余度無刷直流電機有所增大。仿真結果與理論上DR－BLDCM的工作原理一致。

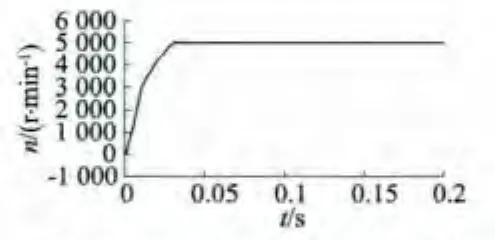
圖4 電機轉速波形(隔槽

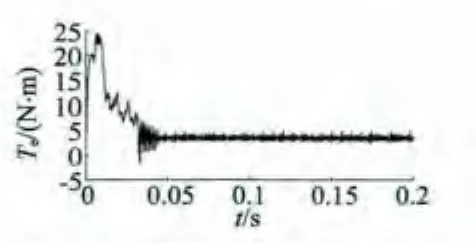
圖5 電機轉矩波形(隔槽)

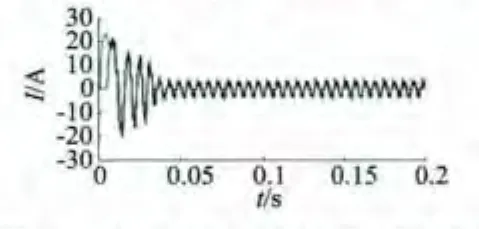
圖6 電機相電流波形(隔槽)

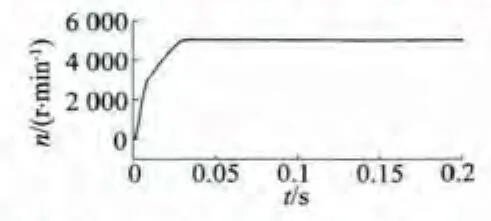
圖7 電機轉速波形(同槽)

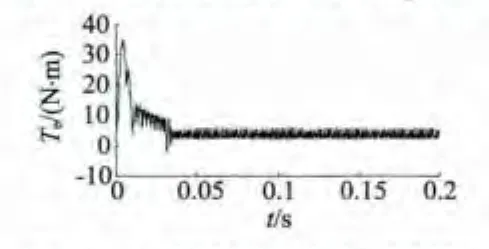
圖8 電機轉矩波形(同槽)

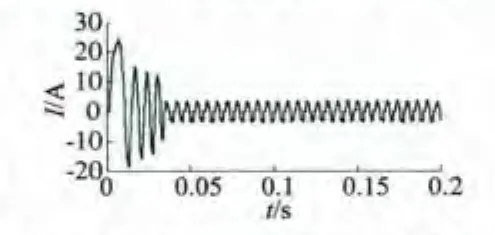
圖9 電機相電流波形(同槽)

3 雙余度無刷直流電機的熱損分析

3.1 銅損分析

計算銅損采用常規方法，即輸入電機的母線電流有效值的平方乘以電樞繞組上的折算電阻。仿真設置假設0.1 s時逆變橋中1通道a相繞組發生斷路。圖10是兩種無刷直流電機銅損仿真波形對比圖。

圖10 銅損仿真波形比較圖

對仿真過程中采集到的數據進行處理后得到如表1所示，p1、p2分別表示余度1繞組銅損、余度2繞組銅損。

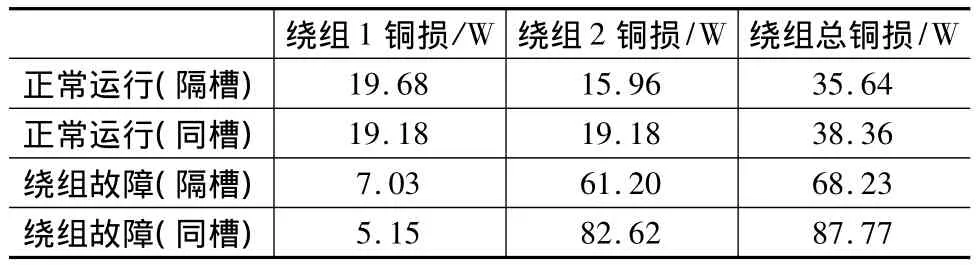
表1 電機兩個余度繞組發熱情況

3.2 鐵耗分析

鐵耗對電機本體的溫升有直接影響，是影響電機性能的重要因素。

本文采用Bertotti分立鐵耗計算模型［9］，是經典的鐵耗計算模型，即:

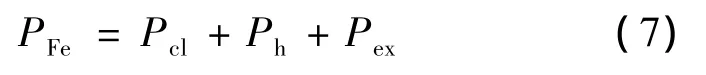
式中:PFe為鐵耗;Pcl為經典渦流損耗;Ph為磁滯損耗;Pex為異常損耗。

根據文獻［9］、［11］，可得到如下簡化鐵耗公式:

式中:Kh、α為磁滯損耗系數;Bm為磁場波的幅值;f為交變磁場波的頻率;Kcl、Kex為經典渦流損耗系數和異常渦流損耗系數;K(Bm)為因局部磁滯環引起的損耗增加系數。

通常局部磁滯環很小，可以忽略其對磁滯損耗的影響，即 K(Bm)≈1。Kh、α、Kcl、Kex與材料成分、物理特性和形狀等因素有關，其中:Kh=0.032 584，α =1.778 5，Kcl=0.000 056，Kex=1.191 9 × 10－7。仿真計算結果如表2所示。

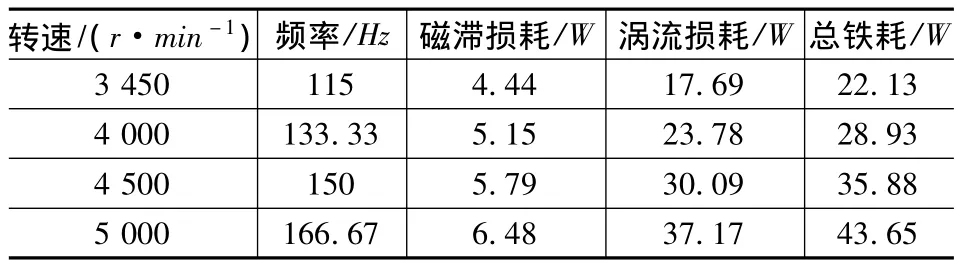
表2 各轉速情況的電機鐵耗

3.3 電機繞組總體熱損

結合表2中仿真得出的銅耗數據與表3的鐵耗數據，就可得到表3及圖11的繞組熱損情況。表中，PFe表示鐵損，PCu表示繞組銅損。

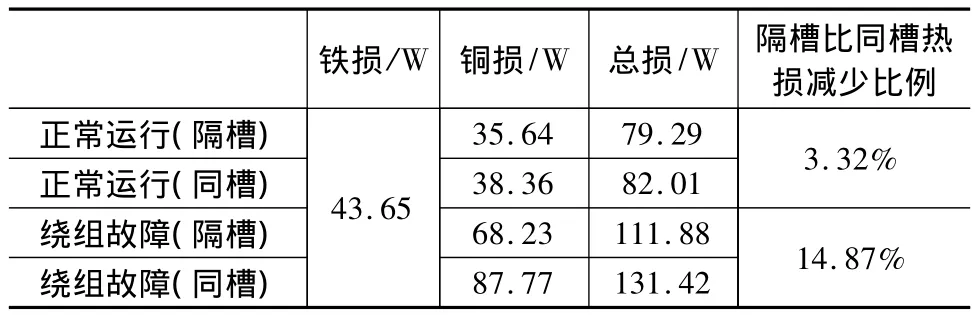
表3 電機繞組總體發熱情況

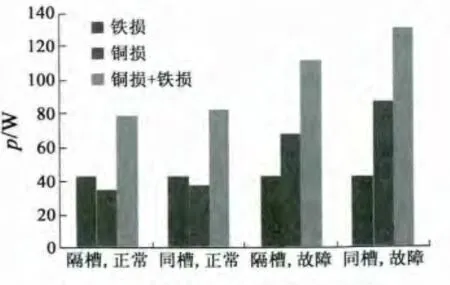
圖11 電機繞組總體發熱情況

4 結 語

本文在分析雙余度無刷直流電機結構特點的基礎上建立了同槽、隔槽雙余度無刷直流電機的數學模型，并在MATLAB/Simulink中建立其仿真模型，進行了正常狀態與繞組斷路狀態的比對性能仿真研究。論文重點關注高空環境下電機熱損分析。對兩種電樞繞組結構的雙余度無刷直流電機的熱損進行了比較，結果表明正常工況下隔槽嵌放的雙余度無刷直流電機熱損相較于同槽嵌放的雙余度無刷直流電機低3%左右，繞組斷路故障工況下，前者熱損比后者低接近15%。

［1］楊平.雙余度無刷直流電機控制系統設計及性能研究［D］.西安:西北工業大學，2005.

［2］付朝陽，劉景林，趙小鵬.雙余度永磁無刷直流電機磁－熱耦合分析［J］.西北工業大學學報，2010，28(6):921 －926.

［3］張明，張一鳴，仝江濤.雙余度無刷直流電機電樞繞組結構對比［J］.微電機，2012，45(2):16 －20.

［4］皇甫宜耿，馬瑞卿，楊永亮.基于RS232串口通信的雙余度無刷直流電動機控制系統［J］.微特電機，2007(5):43－45.

［5］李鐘明，劉衛國.稀土永磁電機［M］.北京:國防工業出版社，1997.

［6］王曉遠，田亮，馮華.無刷直流電機直接轉矩模糊控制研究［J］.中國電機工程學報，2006，26(15):134 －138.

［7］楊永亮.雙余度無刷直流電機控制技術研究［D］.西安:西北工業大學，2007.

［8］李榕，劉衛國，馬瑞卿，等.雙余度無刷直流電機伺服系統電流均衡性研究［J］.電工技術學報，2005，20(9):77 －81.

［9］羅應立，趙海森，姚丙雷，等.交流電機鐵耗的工程計算方法分析［J］.電機與控制應用，2010，37(11):1 －6.

［10］Charles Kingsley.電機學［M］.6版.北京:電子工業出版社，2004.

［11］余莉，胡虔生，易龍芳，等.高速永磁無刷直流電機鐵耗的分析和計算［J］.電機與控制應用，2007，34(4):10－14.