近距空爆載荷作用下疊層薄板抗爆機理數值分析

劉燕紅，陳長海，朱錫，李萬，侯海量，唐廷

近距空爆載荷作用下疊層薄板抗爆機理數值分析

劉燕紅a，陳長海b，朱錫b，李萬c，侯海量b，唐廷b

（海軍工程大學a.動力工程學院；b.艦船工程系；c.兵器工程系，武漢430033）

為探討戰斗部近距爆炸下大尺寸疊層薄板的抗爆機理，結合模型試驗，采用有限元對近距空爆載荷作用下固支疊層方板的爆炸載荷、變形過程、應變分布和變形吸能情況進行了數值分析，并與相同材料同等總厚度的單層方板進行了比較。在此基礎上，進一步分析了層間間距、疊層層數和邊界條件對疊層板抗爆性能的影響。結果表明，較單層板而言，試驗工況下疊層板的變形吸能較大，但其最大應變較小且應變分布更為均勻；而在極限應變狀態下，疊層板變形吸能較單層板有很大提高；適當增大層間間距能一定程度地提高疊層板的抗爆變形能力，但過大的層間間距不利于疊層板的整體協調變形；層數的增加能提高疊層板的抗爆變形能力；簡支邊界條件較固支邊界條件而言，能更充分地發揮疊層板的抗爆變形吸能能力。

爆炸力學；近距空爆載荷；疊層薄板；抗爆機理；數值分析

1 引言

爆炸載荷作用下金屬結構主要通過塑性大變形來吸收沖擊波能量。而對于金屬平板結構而言，爆炸載荷作用下沖擊波能量大部分通過結構的彎曲和薄膜拉伸這兩種塑性大變形的方式耗散掉[1-2]。而爆炸載荷作用下薄板在產生大變形的情形下，薄膜拉伸效應較為明顯，此時彎曲應變效應往往可以忽略[2-4]。文獻[2-4]對金屬薄板結構的薄膜效應進行了理論分析，并指出爆炸載荷下薄板應盡可能設計成工作在薄膜應力狀態下，這樣可以更有效地發揮其抗爆吸能能力。基于這一思想，本文提出多層薄板結構即疊層板結構，并試圖通過數值仿真分析其抗爆機理。目前，關于爆炸載荷下金屬薄板的動態響應及其失效模式的研究較多，包括圓板[5-6]、方板[7-9]和矩形薄板[10]等。最近，研究者們對爆炸載荷下加筋板的動態響應問題開展了大量的試驗[11-12]和數值仿真[13]研究。然而，這些研究大多集中于單層平板或板架，對于多層薄板結構的抗爆問題研究較少。文獻[14]開展了雙層間隔鋼板的抗爆試驗，然其主要目的是與雙層泡沫夾芯結構進行對比，未見有雙層無間隔鋼板的分析。此外，近年來出現了大量關于雙層平板夾芯結構抗爆響應問題的研究，如文獻[15-17]，但均與本文所提出的疊層板結構的抗爆響應問題存在較大差異。

隨著反艦武器的發展，掠海飛行的半穿甲導彈已成為現代水面艦船面臨的主要威脅，其作用方式通常是穿透舷側外板后在艦船內部艙壁附近爆炸。因此，如何使內部艙壁結構在近距空爆載荷作用下盡可能多地吸收爆炸沖擊波能量，以最大限度地減小沖擊波對鄰近艙室的毀傷程度和毀傷范圍，成為艦船抗爆防護結構設計的重點。而本文提出的疊層板結構應該能夠滿足艦船抗爆防護結構設計中的抗爆吸能要求，但是目前對于其在近距空爆載荷作用下抗爆機理問題的研究還未見報道。

本文擬采用有限元數值仿真，結合模型試驗，對近距空爆載荷作用下固支大尺寸疊層薄板結構的抗爆機理進行分析，并與相同材料同等總厚度的單層板進行比較。通過比較得到疊層板結構相對于單層板抗爆性能優劣的情況，并進一步分析疊層板抗爆性能的影響因素。

2 試驗設計與實施

試驗模型為一疊層板，該疊層板由4塊1 mm厚的Q235低碳鋼板疊層放置而成，4塊薄鋼板的總體尺寸均為700 mm×700 mm。試驗中邊界條件很重要，為此專門設計了一個方形鋼質支座結構作為試驗固定裝置，支座的框架夾具面板厚度為20 mm。試驗時將鋼板夾于框架面板和底部支座之間，四周通過24個螺栓固定，以保證模型邊界不會出現較大的面內移動。由于框架夾具面板四周有一定寬度，因而模型的實際抗爆面積為500 mm×500 mm，整個支座的高度為200 mm。試驗時，將TNT炸藥置于模型中心的正上方，并用繩子將炸藥的位置固定(見圖1)。試驗條件為：裝藥量為400 g，裝藥形式為柱狀，裝藥尺寸131.2 mm×50.2 mm，爆距為148 mm。為了比較，對單塊4 mm厚的Q235鋼板也進行了試驗，其尺寸與疊層板相同，試驗條件也與疊層板完全一致。為便于分析，稱單層板試驗為工況1，疊層板試驗為工況2。

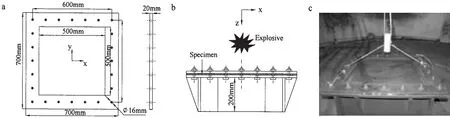
圖1 試驗裝置示意圖和照片Fig.1 Sketch and photograph of the experimental setup

3 有限元計算模型

式中：σd為動態屈服強度；σ0為靜態屈服強度；Eh為應變硬化模量；εp為有效塑性應變；ε˙為等效塑性應變率；D、n為常數，對于低碳鋼，通常取D=40.4/s，n=5。材料失效模型采用最大等效塑性應變失效準則。鋼板的材料參數通過準靜態試驗獲得，具體參數為：密度ρ=7.8 g/cm3，彈性模量E=210GPa，泊松比ν=0.3，準靜態屈服強度σ0=235 MPa，應變硬化模量Eh=250 MPa。考慮到近距空爆載荷作用下結構的應變率效應較大，且中心點處易產生拉伸失效，因此仿真計算中材料的失效應變取為εf=0.411[18]。

炸藥和空氣均采用DMAT歐拉單元。炸藥的爆轟過程通過JWL狀態方程描述：

采用動態非線性有限元分析程序MSC/Dytran模擬結構的動態響應。仿真計算中，疊層板各層以及單塊板均采用四邊形殼單元進行模擬，邊界條件均為四邊固支。疊層板各層之間的間距為0.05 mm，各層之間定義了自適應接觸，以避免單元畸變，同時也是為了模擬實際抗爆過程中各層之間的接觸碰撞過程。

鋼板材料采用雙線性彈塑性本構模型，材料的應變率效應由Cowper-Symonds（C-S）模型描述：

式中：p為壓力，A、B、R1、R2和ω為常數，η=ρ/ρ0，ρ0為初始密度；e為炸藥的質量比內能。仿真計算中TNT炸藥的各材料參數為：A=52.42 GPa，B=0.768 GPa，R1=4.2，R2=1.1，ω=0.34，e=4.19 kJ/g，初始密度ρ0=1.54 g/cm3。假設空氣為無粘性理想氣體，沖擊波在空氣中的傳播用理想氣體狀態方程模擬，即：

式中：γ為絕熱指數，e為空氣的質量比內能。空氣介質的狀態參數為：初始密度ρ0=1.29 kg/cm3，初始壓力p0=101 kPa，絕熱指數γ=1.4，初始比內能e=0.197 kJ/g。空氣邊界為可流入流出邊界。歐拉單元與拉格朗日單元之間的耦合采用一般耦合方式，通過建造虛擬單元來形成封閉耦合面，仿真計算模型如圖2所示。

4 仿真計算與試驗結果比較分析

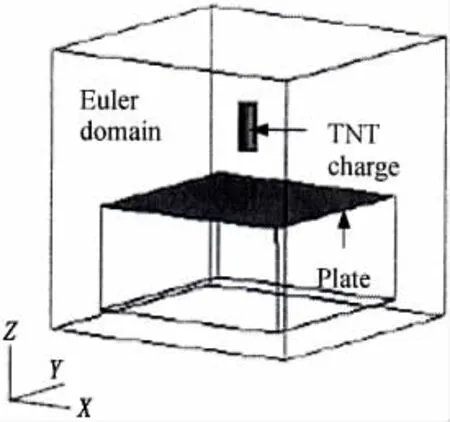
圖2 仿真計算模型示意圖Fig.2 Schematic of the model for numerical simulation

工況1試驗后單層板的變形如圖3a所示。由圖可看出，在板的中部出現了明顯的“燒灼”現象，“燒灼直徑”約為100 mm，這種現象是由于炸藥對板材的爆轟褪色作用引起的[6-10]。在“燒灼”區域的外圍出現了較大的碟形變形區，變形大體上是對稱的，而在板的對角線處出現了不明顯的塑性鉸線。通過測量得到板中心的最大撓度為42.3 mm。仿真計算得到的單層板最終變形如圖3b所示。計算結果顯示，t=1.0 ms時刻后，板的變形趨于穩定，存在小量的彈性振動。從圖3b可看出，板中心部位出現了一個圓形變形區，直徑約為120 mm，這比試驗得到的“燒灼”區的直徑稍大。仿真計算得到的單層板中心點處最大位移時程曲線如圖4所示，從圖中可以看到單層板響應后期的彈性振動現象。通過對1.0 ms時刻以后板中心點處的最大位移取平均值，得到單層板中心的最大撓度約為42.1 mm，較試驗值稍小。

圖3 工況1單層板的變形比較Fig.3 Comparison of deformation for single-layer plate in case 1

圖4 板中心點處最大位移時程曲線Fig.4 History of maximum displacement at centre points of the plates

圖5 工況2疊層板的變形比較Fig.5 Comparison of deformation for multilayered plate in case 2

圖5a為工況2試驗后疊層板的整體變形圖。從圖中可看出，板對角線處出現了明顯的塑性鉸線。此工況中也存在燒灼現象。“燒灼直徑”約為102 mm，與工況1中的“燒灼直徑”值接近。這是由于工況1和工況2兩種工況之間試驗條件相同所致。疊層板“燒灼”區以外也出現了碟形變形區，不過該碟形變形區的面積較單層板要大得多。通過測量得到疊層板中心點處最大位移為47.3 mm。圖5b為t=0.8 ms時刻仿真計算得到的疊層板變形圖，該時刻以后整個疊層板的變形趨于穩定，并存在一定程度的彈性振動。由于各層之間的位移變化基本一致，因此圖4中疊層板的位移取的是四層板中心點處位移w0的平均值。比較圖3b和圖5b可看出，相比單層板而言，疊層板邊界出現了明顯的塑性變形，中部碟形變形區的大小較單層板要大得多，這與試驗結果是一致的。此外，疊層板的變形穩定時間較單層板要早。這是由于疊層板總體的剛度較單層板要小，在抗爆過程中的橫向變形速度較大所致。疊層板中心點處最大位移隨時間的變化情況如圖4所示。通過對0.8 ms時刻以后疊層板中心點處的最大位移取平均值，得到疊層板的最大撓度為45.1 mm，較試驗值要小。這主要是由于試驗過程中疊層板邊界出現了一定程度的褶皺現象（圖5c），使得疊層板產生了一定的面內位移，從而導致試驗結果偏大。通過與試驗結果的比較可知，仿真計算結果與試驗結果吻合較好，驗證了數值仿真算法的合理性和可靠性。

5 試驗工況下疊層板抗爆機理對比分析

5.1 爆炸載荷分析

炸藥近距爆炸下，結構承受的載荷為強動載荷，局部效應較為明顯，且在沖擊波載荷作用初期，存在爆炸流場與結構的流固耦合效應[19]。由于此耦合效應的存在，使得疊層板迎爆面反射沖擊波壓力的作用過程與單層板（以下均指材料和總厚度均與疊層板一致的單層板）出現較大差別。圖6給出了本文試驗條件下，仿真計算得到的工況1單層板和工況2疊層板中心點處反射沖擊波壓力時程曲線。從圖中可看出，在沖擊波作用初期，疊層板的反射沖擊波壓力峰值較單層板要小。這是由于在沖擊波載荷作用初期，疊層板只有第一層直接承受沖擊波載荷，而單層板則是整塊板，因而根據流固耦合作用原理可知[20]，質量較輕的疊層結構加速度較大，其在沖擊波作用過程中能夠有效減小結構表面的反射沖擊波壓力峰值。而從另一方面來理解，則是由于單層板直接承受載荷的慣性質量較大且剛度較大，使得其反射沖擊波的峰值壓力較疊層板結構要大，這與加筋板局部爆炸沖擊載荷研究的結論是一致的[21]。

從圖6中可進一步看出，在沖擊波作用后期即反射沖擊峰值壓力過后，單層板表面反射沖擊波壓力迅速衰減，而疊層板結構表面反射沖擊波壓力的衰減速度較單層板要慢。這主要是由于局部沖擊載荷下結構的表面效應引起的[22]，即連續的結構表面的形狀變化以及結構的持續運動使得反射沖擊波壓力發生改變，進而使得反射沖擊波的持續時間也發生變化。疊層板結構由于彎曲剛度較小，中點處的運動速度大，形狀改變得較快，因而沖擊波持續作用的時間較單層板要長，反射沖擊波的衰減速度較單層板要慢。

5.2 變形過程分析

近距空爆載荷下，固支大尺寸方板的變形過程與小尺寸方板存在較大差異。對于大尺寸方板而言，邊界的變形較小，局部效應更為明顯[23]。圖7為工況1爆炸載荷下單層板動態變形過程的等高線。由圖可知，單層板的變形首先從中部產生，然后向邊界擴展。當t=0.4 ms左右，變形擴展至邊界。當t= 1.0 ms左右變形趨于穩定，形成類似于“四坡頂形”的變形機構，對角線處形成不太明顯的塑性鉸線。計算結果顯示，相對于板的中部而言，單層板邊界附近的變形位移值很小，變形集中于板的中部。

圖6 中心點處反射沖擊波壓力時程Fig.6 History of reflected shock wave pressure at centre point

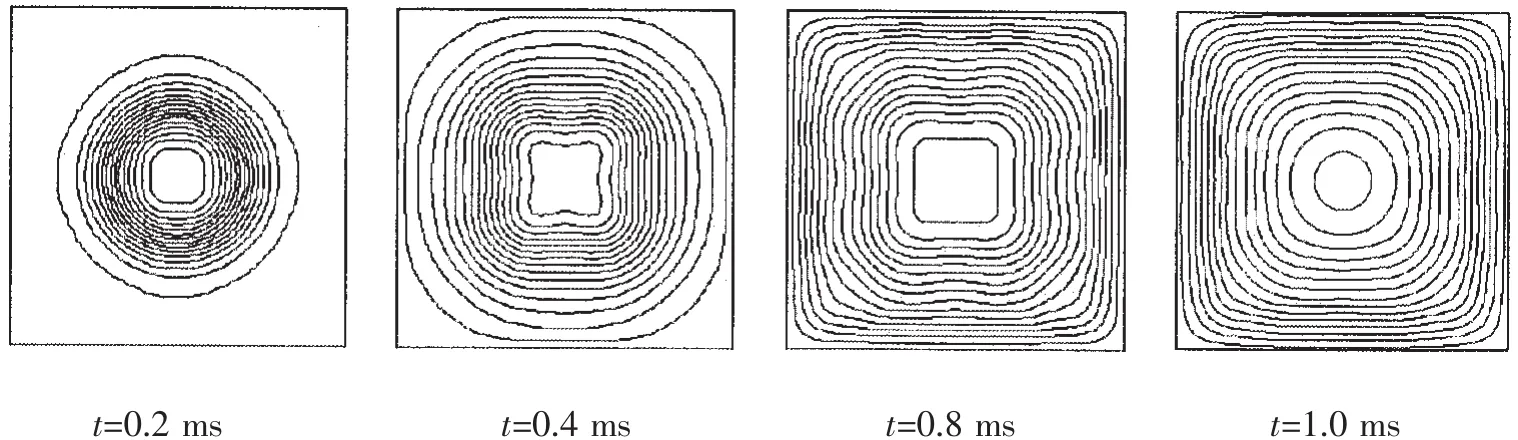
圖7 單層板的變形等高線Fig.7 Deformation contour line of single-layer plate

與單層板不同的是，疊層板的變形過程要更為迅速，這主要是由于疊層板的剛度較小所致。圖8給出了疊層板第一層的動態變形過程的等高線。當t=0.2 ms左右，疊層板的變形就已擴展至邊界。隨后，由于疊層板各層之間存在短暫的碰撞和動量傳遞過程，疊層板各層的變形迅速均勻化，并在對角線處出現塑性鉸線。當t=0.8 ms左右，疊層板的變形趨于穩定，并在對角線處形成較明顯的塑性鉸線。計算結果顯示，疊層板邊界附近的變形位移值較單層板邊界附近要大。進一步比較圖8和圖7可知，盡管疊層板的變形模式與單層板相似，但其變形速度及其最終變形程度均較單層板要大。

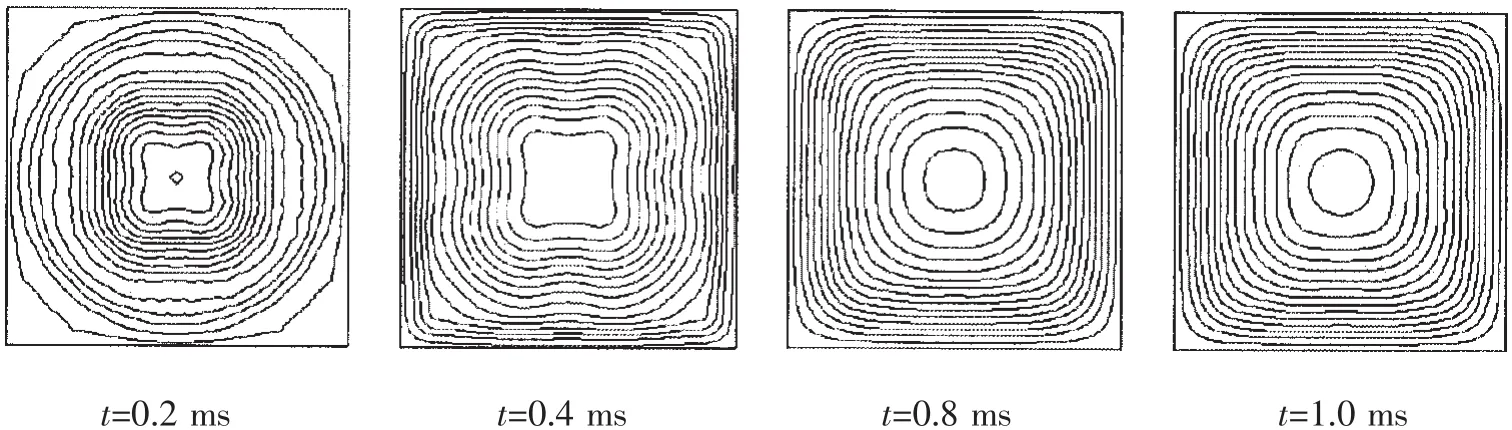
圖8 疊層板（第一層）的變形等高線Fig.8 Deformation contour line of multilayered plate(the first layer)

5.3 應變分布分析

為了對比分析疊層板和單層板變形機理的差異，對單層板和疊層板中薄膜拉伸應變和彎曲應變的分布及其程度進行分析。如圖9所示，取板的1/4對稱平面，沿坐標x軸方向和對角方向分別選取兩組單元，每組包含11個單元，自坐標原點（即板的中心點）處的單元往邊界依次編號。組1（即Group 1）的單元沿板中線x軸方向，組2（即Group 2）的單元沿板的一條對角方向。仿真計算過程中，分別提取所選取單元的應變值進行分析。需要指出的是，疊層板結構取的是第四層板上的單元。薄膜拉伸應變水平可由仿真計算得到的單元中面應變εmid表示，而彎曲應變的程度則可通過計算單元上下表面應變的差值得到，即εd=εlower-εupper，其中εd表示單元彎曲應變的程度，εlower表示單元下表面的應變，εupper表示單元上表面的應變。

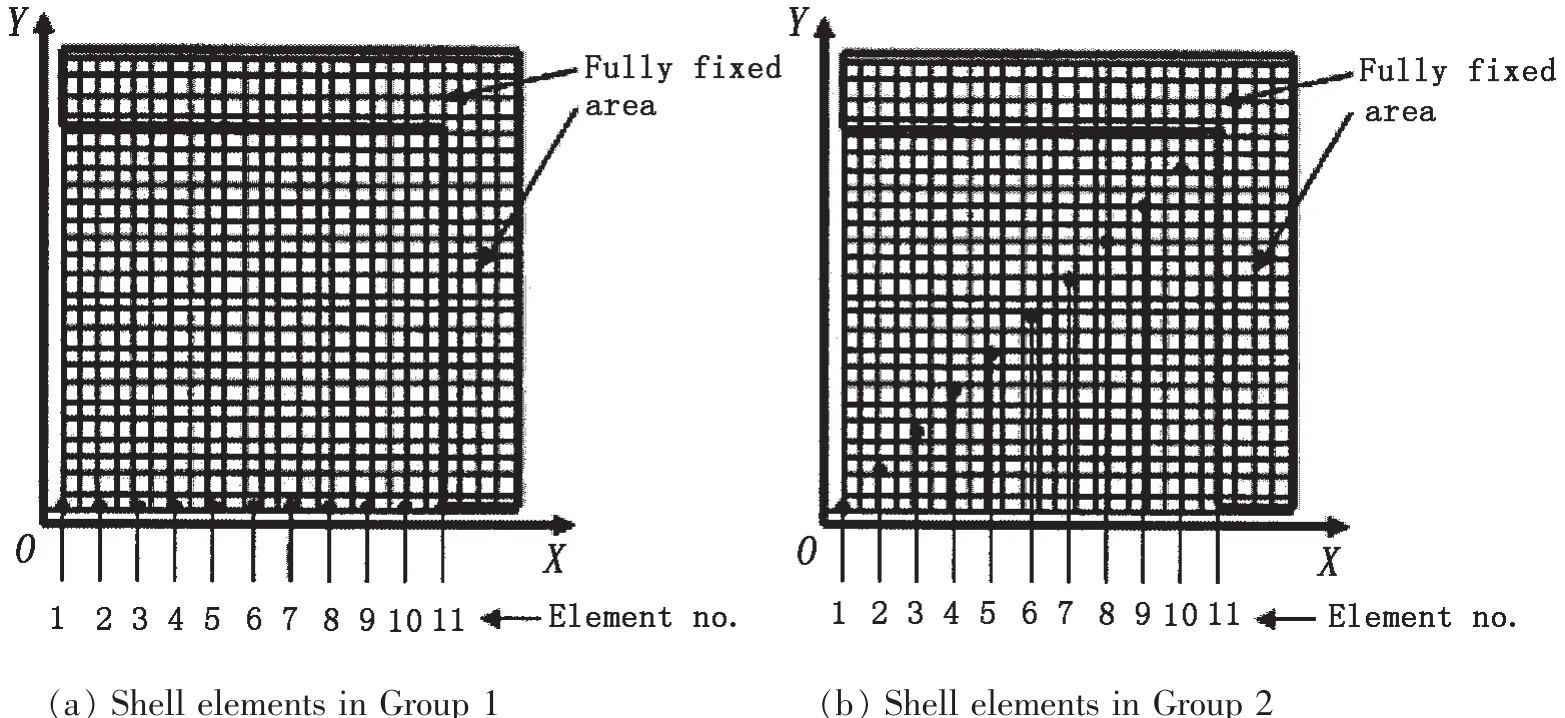
圖9 兩組所選取單元的位置Fig.9 Locations of the selected elements in the two groups

單層板沿x軸方向（即組1）各單元的應變發展及最終的應變分布如圖10所示。由圖10a和b可看出，εmidx和εmidy均隨時間增長而增大，且應變自邊界沿板的中心擴展。當t=1.0 ms左右，中心點處的中面應變εmidx和εmidy達到最大，均為2.2%。而在邊界附近，單元的應變很小。由此可見，對于單層板而言，最大的薄膜拉伸應變發生在板的中心，邊界附近的拉伸應變幾乎為0，即邊界附近幾乎沒有發生拉伸變形。

圖10 單層板沿x軸方向（組1）單元應變分布Fig.10 Strain distribution of the shell elements along the x axis(Group 1)in single-layer plate

圖10c和d為單層板沿x軸方向各單元的彎曲應變水平的分布情況。由圖10c可看出，彎曲應變隨時間的增長而增大。邊界附近的彎曲應變很小，而在中心部位，彎曲應變最大。結合圖10d可進一步看出，彎曲應變像波浪一樣，從固支邊界向中心部位傳播。當t=1.0 ms左右，板的變形趨于穩定，最大的彎曲應變發生在板的中心部位，而邊界附近的彎曲應變很小甚至出現負值。

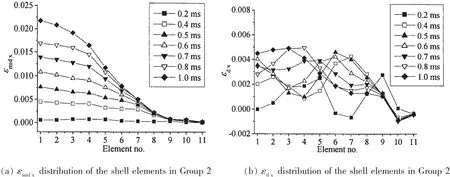
圖11 單層板沿對角方向（組2）單元應變分布Fig.11 Strain distribution of the shell elements along a diagonal(Group 2)in single-layer plate

圖11給出了單層板沿對角方向各單元的應變發展及最終分布情況。由于對稱性，只給出了εmidx和εdx的分布情況。由圖11a可看出，單層板沿對角方向單元的薄膜拉伸應變分布情形與沿x軸方向相似。而從圖11b則可看出，與沿x軸方向類似，單層板對角線方向εdx也呈現出波浪形的傳播現象，且穩定狀態下，最大彎曲應變也發生在板的中心部位，邊界附近的彎曲應變很小甚至出現負值。

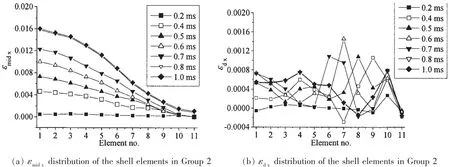
圖13 疊層板沿對角方向（組2）單元應變分布Fig.13 Strain distribution of the shell elements along a diagonal(Group 2)in multilayered plate

疊層板沿x軸方向（即組1）各單元的應變發展及最終的應變分布如圖12所示。通過比較圖12a-b與圖10a-b可知，盡管疊層板沿x軸方向單元的εmidx和εmidy的最大值也均發生在中心部位，但疊層板εmidx和εmidy的分布較單層板要更為均勻；雖然疊層板邊界附近的薄膜拉伸應變較單層板要大，但其中心部位的最大薄膜拉伸應變卻較單層板要小，即中心部位的εmidx和εmidy分別為1.6%和1.7%。

進一步比較圖12c-d與圖10c-d可得，疊層板沿x軸方向彎曲應變的分布形狀與單層板相似，呈現波浪式的形狀，最大彎曲應變也發生在中心部位，邊界附近的彎曲應變也很小。不同之處在于，疊層板沿x軸方向整體的彎曲應變水平較單層板要小得多，這主要是由于疊層板各層的厚度較小所致。

圖13為疊層板沿對角方向（即組2）各單元的應變分布情況。比較圖13a和圖11a可知，疊層板沿對角方向各單元的薄膜拉伸應變分布較單層板要均勻，邊界附近的薄膜拉伸應變較單層板要大，但中心部位的最大薄膜拉伸應變較單層板要小。圖13b為疊層板對角方向各單元的彎曲應變變化及分布情況。與疊層板沿x軸方向的彎曲應變分布（圖12d）不一樣的的是，對角方向上的彎曲應變雖然也呈現出波浪式的分布，但其在變化過程中以及最終穩定情形下，對角方向上的最大彎曲應變并不在疊層板的中心部位，且體現出較強的時間和位置敏感性。這正是由于疊層板在變形過程中，塑性鉸線沿對角線方向由邊界向中心運動所引起的[17]。進一步比較圖13b和圖11b可知，單層板對角線方向的彎曲應變沒有像疊層板一樣出現較大的時空敏感性，說明其對角線方向上塑性鉸線的影響較小，而疊層板對角線上塑性鉸線的影響較大。由此可得，疊層板對角線上的塑性鉸線較單層板要明顯，試驗結果也證明了這一點。

5.4 變形吸能分析

由上節對疊層板和單層板應變分布的分析可知，疊層板的薄膜拉伸變形是主要的變形機理，彎曲變形很小且可忽略。由此可見，疊層板獲得的絕大部分動能都將以薄膜拉伸變形的方式耗散掉。圖14比較了仿真計算得到的試驗工況下單層板和疊層板的整體變形吸能情況。由圖可知，疊層板的整體變形吸能量要大于單層板，這主要得益于疊層板的薄膜拉伸變形分布較單層板要均勻。結合上節的應變分析可得，疊層板的整體變形吸能量較單層板要大，而其最大塑性應變較單層板要小。由此可見，近距空爆載荷下，疊層板的抗爆變形能力要明顯優于相同材料和厚度的單層板。

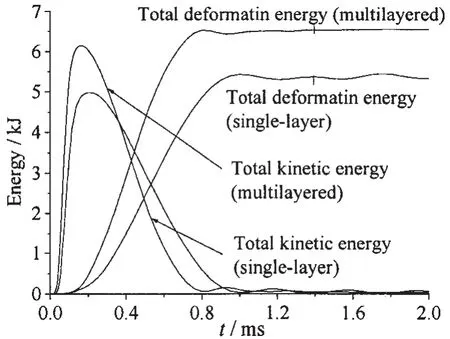
圖14 變形吸能比較Fig.14 Comparison of deformation energy absorption

6 極限應變狀態下疊層板的變形吸能分析

通過對試驗工況下疊層板抗爆機理的分析可看出，試驗工況下疊層板和單層板的最大應變均遠小于材料的失效應變，即試驗工況下疊層板和單層板均遠未達到結構失效破壞時的臨界狀態（即極限應變狀態）。而工程實際中，設計者們可能更為關心的是極限應變狀態下疊層板的變形吸能情況。因此，本文在對試驗工況仿真的基礎上，通過增加藥量，使疊層板和單層板達到各自的極限應變狀態。由于仿真計算中很難控制藥量使結構剛好達到極限應變狀態，因此本文仿真計算的極限應變工況中疊層板和單層板的最大應變在0.40至0.41之間。圖15給出了相應的極限應變狀態下，疊層板和單層板沿x軸方向（組1）單元的應變分布比較，疊層板的應變取的是相應位置處四層板單元的平均應變值。考慮到極限應變狀態下單層板的彎曲效應較明顯，因而此節比較的是疊層板和單層板各自單元的有效塑性應變值εeq。從圖15中可看出，疊層板的應變分布明顯較單層板要均勻得多。計算結果顯示，極限應變狀態下，疊層板的薄膜拉伸應變較單層板要大且分布更為均勻，而單層板的彎曲應變較大，尤其在邊界部位及其附近表現得更為明顯。而正是由于邊界單元彎曲應變較大，使得單層板沿x軸方向單元的有效塑性應變并未呈現單調遞減的變化趨勢。如圖15所示，盡管單層板的最大有效塑性應變仍位于中心點處，但邊界處的有效塑性應變并不是最小。

結合對圖15應變分布的分析可知，疊層板中心部位以外的區域有效塑性應變較大且分布較為均勻，應變梯度較小，這說明抗爆過程中疊層板的整體變形吸能能力發揮得更為充分。而計算結果顯示，疊層板的有效塑性應變中薄膜拉伸應變較彎曲應變要大得多，這說明疊層板主要通過薄膜拉伸變形進行吸能，圖16為極限應變狀態下，疊層板和單層板的總體變形吸能比較。由圖可知，疊層板的總體變形吸能較單層板要大得多。從具體總吸能量來看，疊層板的總變形吸能較單層板約大65.1%。由此可見，極限應變狀態下，疊層板的變形吸能能力較單層板有很大提高。應該指出的是，疊層板的極限應變計算工況中炸藥的藥量約為單層板計算工況的1.25倍，這說明極限應變狀態下疊層板抗爆承受能力較單層板稍強。

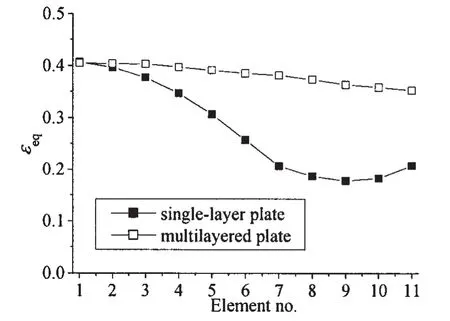
圖15 極限應變狀態下應變分布比較Fig.15 Comparison of strain distributions underultimate strain conditions

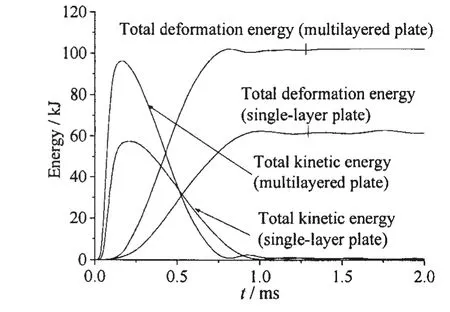
圖16 極限應變狀態下變形吸能比較Fig.16 Comparison of deformation energy absorptions under ultimate strain conditions

7 疊層板抗爆性能影響因素分析

7.1 層間間距影響

結合模型試驗工況，進一步分析了層間間距對疊層板應變分布的影響。圖17為在模型試驗工況2下，疊層板層間間距的變化對其應變分布的影響。需要說明的是，此處分析的層間間距是指各層層間間距相同的情形。通過5.3節對應變分布的分析可知，彎曲應變很小且可忽略，因此此處只分析疊層板第4層的薄膜拉伸應變，取疊層板第4層沿x軸方向（組1）單元εmidy應變進行分析。由圖17可看出，隨層間間距的增大，疊層板第4層的應變不斷減小，且邊界附近應變減小較明顯。這是由于，一方面結合5.1節爆炸載荷的分析可知，層間間距的增大能在一定程度上減小反射沖擊波的峰值壓力；另一方面，層間間距的增大使得傳遞至疊層板背層的動量減小。圖18給出了疊層板層間間距為5 mm的情形下，各層的應變分布情況。由圖可知，雖然疊層板第4層的應變有所減小，但其第1層的應變卻明顯增大，且各層之間應變梯度較大。這顯然是由于過大的層間間距不利于疊層板各層之間的協調變形所致。

圖17 不同層間間距下疊層板（第4層）的應變分布Fig.17 Strain distributions of the multilayered plates(the 4th layers)with different interlayer spaces

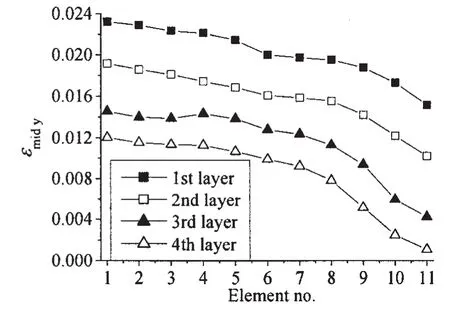
圖18 層間間距為5 mm時疊層板各層的應變分布Fig.18 Strain distributions of the layers in the multilayered plate with 5mm interlayer space

通過以上分析可得，一定載荷工況下，在一定范圍內，適當地增大疊層板的層間間距能減小其背層的應變大小；但過大的層間間距不利于疊層板整體協調變形，從而不能充分發揮其抗爆變形能力。

7.2 疊層層數影響

圖19給出了相同總厚度下，具有不同層數（4、6和8層）疊層板背面最后一層沿x軸方向（組1）單元在t=2.0 ms時刻εmidy應變的分布情況，該時刻各疊層板塑性變形均趨于穩定。由圖可知，在相同近爆工況下，柔性疊層板結構的層數越多，其最大應變越小，應變分布越均勻，說明其抗爆變形能力越強。然而當層數過大時（在本計算工況下為大于4層），其應變減小的幅度相對變小，這說明過多的層數對于疊層板抗爆變形能力的提高并不明顯。由于疊層板主要是通過減小各層板的彎曲應變，提高其薄膜拉伸變形能力來提高其整體抗爆變形能力的，因此過多的層數對于疊層板各層彎曲應變的減小以及薄膜拉伸變形能力的提高效果并不明顯。考慮到工程實際中，層數越多其施工工藝越復雜，因此疊層板層數的選取不宜過多。

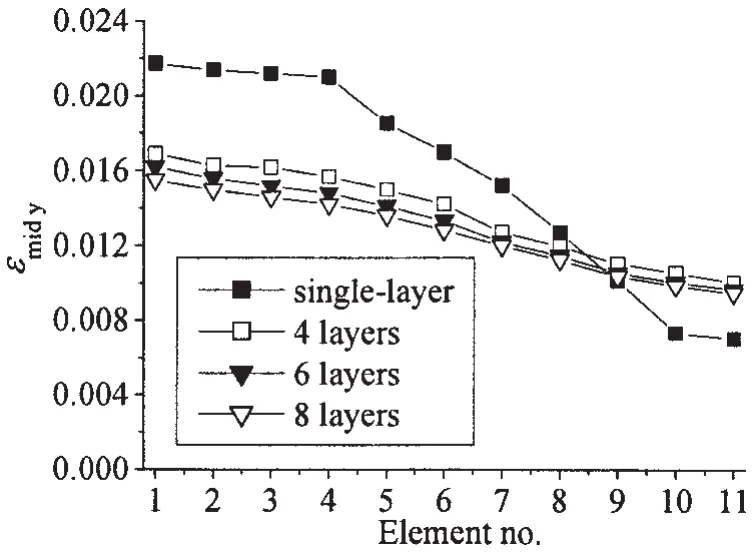
圖19 疊層板的層數對其應變分布的影響（t=2.0 ms）Fig.19 Effect of layer number on the strain distributions of the multilayered plates(t=2.0 ms)

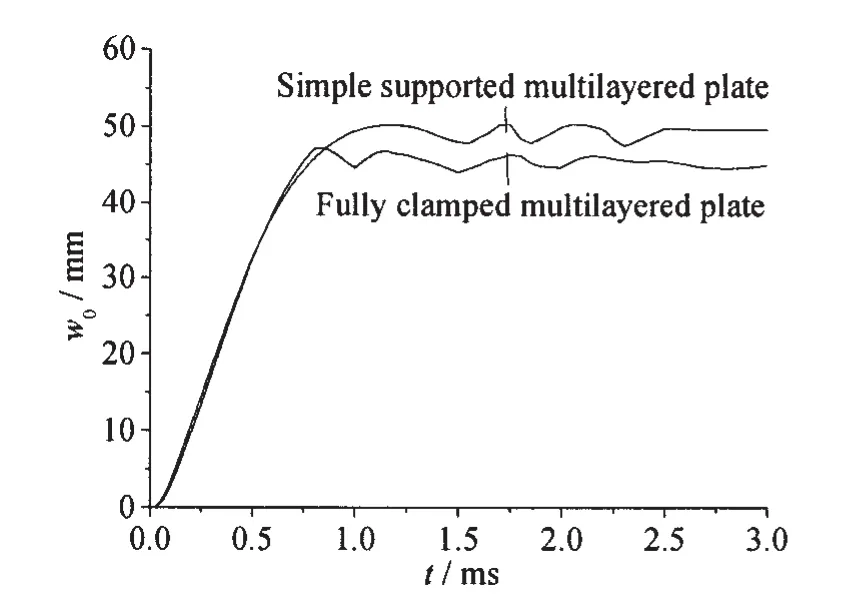
圖20 邊界條件對疊層板位移時程的影響Fig.20 Effect of boundary conditions on displacement histories of multilayered plates

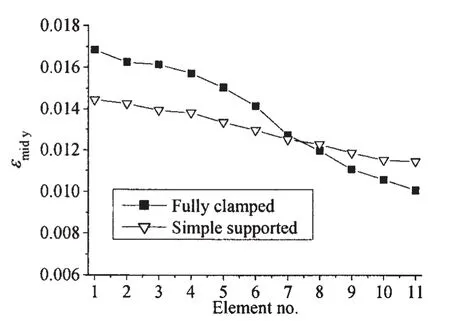
圖21 邊界條件對疊層板應變分布的影響（t=1.5 ms）Fig.21 Effect of boundary conditions on strain distributions of multilayered plates(t=1.5 ms)

圖22 邊界條件對疊層板（4層）吸能的影響Fig.22 Effect of boundary conditions on energy absorptions of multilayered plates(4 layers)

7.3 邊界條件影響

為進一步分析邊界條件對疊層板抗爆性能的影響，對試驗工況2疊層板在簡支邊界條件下的情形進行了仿真計算，并與固支邊界條件下的計算結果進行了比較。圖20和21分別為兩種邊界條件下疊層板位移時程曲線和變形吸能曲線的比較，其中圖20疊層板的位移均取的是四層板中心點處位移w0的平均值。圖21均取的是疊層板第4層沿x軸方向（組1）單元t=1.5 ms時刻εmidy應變值。由圖20可看出，簡支邊界條件下疊層板中心點處的最終位移要大于固支邊界的情形，由此可見簡支邊界條件下疊層板的整體變形程度較固支邊界要大。然而，從圖21中的應變分布情況來，簡支邊界條件下疊層板的最大應變并不比固支邊界的大。從圖21中可看出，簡支邊界條件下疊層板邊界附近的應變較固支邊界要大，然中心點處的應變較固支邊界要小，從而使得簡支邊界條件下疊層板的應變分布較固支邊界要更為均勻，整體抗爆變形能力能得到更有效地發揮。從圖21中還可看出，由于本文所研究的疊層板的尺寸相對較大，因而其最大應變仍發生于中心點附近。若疊層板的尺寸相對較小，則簡支邊界條件下其最大應變有可能首先產生于邊界中點附近，從而會出現如文獻[9]中得到的沿邊界拉伸撕裂的失效破壞模式。圖22為簡支和固支兩種邊界條件下疊層板的變形吸能情況比較。通過比較可知，簡支邊界條件下疊層板的整體變形吸能量較固支邊界大約17%。由此可見，相同近距空爆載荷工況下，簡支邊界條件較固支邊界而言，能較大程度地提高疊層板的抗爆吸能能力。結合圖21對應變分布的分析可知，這是由于簡支邊界條件下疊層板整體變形程度較大且應變分布較均勻，因而能更好地發揮疊層板的薄膜拉伸變形吸能能力。

8 結論

結合模型試驗，采用有限元對固支大尺寸疊層方板在近距空爆載荷作用下的抗爆機理進行了數值仿真分析，并與相同材料同等厚度的單層板進行了比較。最后，探討了層間間距等因素對疊層板抗爆性能的影響。得到以下主要結論：

（1）相同的近距空爆載荷工況下，與同等總厚度的單層板相比，疊層板的變形吸能較大，但最大應變較小且應變分布更為均勻；而極限應變狀態下疊層板的變形吸能較單層板要大得多，因而疊層板整體抗爆變形吸能能力明顯優于單層板。

（2）一定范圍內，適當地增大疊層板的層間間距能提高其抗爆變形能力，但過大的層間間距不利于疊層板的整體協調變形，從而不能充分發揮其整體抗爆變形能力。

（3）疊層板層數的增大對其整體抗爆變形能力的提高有一定效果，然而過多的層數對其抗爆變形能力的提高效果并不明顯。

（4）較固支邊界條件而言，簡支邊界條件能使疊層板的最大應變降低且應變分布更為均勻，因而能較大程度地提高疊層板的抗爆變形吸能能力。

[1]吳有生,彭興寧,趙本立.爆炸載荷作用下艦船板架的變形與破損[J].中國造船,1995(4):55-61.

Wu Yousheng,Peng Xingning,Zhao Benli.Plastic deformation and damage of naval panels subjected to explosion loading[J].Shipbuilding of China,1995(4):55-61.(in Chinese)

[2]彭興寧,聶武,嚴波.爆炸載荷作用下艦船防護艙壁的薄膜效應研究[J].船舶力學,2007,11(5):744-751.

Peng Xingning,Nie Wu,Yan Bo.Analysis of membrane effect of surface warship’s protective bulkhead subjected to blast loading[J].Journal of Ship Mechanics,2007,11(5):744-751.(in Chinese)

[3]Symond P S,Wierzbiki T.Membrane mode solutions for impulsively loaded circular plates[J].J Appl Mech,1979,46:58-63.

[4]Wierzbicki T,Nurick G N.Large deformation of thin plates under localised impulsive loading[J].Int J Impact Eng,1996, 18(7-8):899-918.

[5]Teeling-Smith R G,Nurick G N.The deformation and tearing of thin circular plates subjected to impulsive loads[J].Int J Impact Eng,1991,11(1):77-91.

[6]Nurick G N,Radford A M.Deformation and tearing of clamped circular plates subjected to localised central blast loads[C]// In:Recent Developments in Computational and Applied Mechanics.Barcelona,Spain,1997:276-301.

[7]Olson M D,Nurick G N,Fagnan J R.Deformation and rupture of blast loaded square plates-predictions and experiments [J].Int J Impact Eng,1993,13(2):279-291.

[8]Nurick G N,Shave G C.The deformation and tearing of thin square plates subjected to impulsive loads-an experimental study[J].Int J Impact Eng,1996,18(1):99-116.

[9]朱錫,馮剛,張振華.爆炸載荷作用下固支方板的應變場及破壞分析[J].船舶力學,2005,9(2):83-89.

Zhu Xi,Feng Gang,Zhang Zhenhua.Strain field and damage analysis of clamped square plates subjected to explosive loading[J].Journal of Ship Mechanics,2005,9(2):83-89.(in Chinese)

[10]Jacob N,Chung Kim Yuen S,Nurick G N.Scaling aspects of quadrangular plates subjected to localised blast loads-experiments and predictions[J].Int J Impact Eng,2004,30(8):1179-1208.

[11]Chung Kim Yuen S,Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates. Part I:Subjected to uniform blast load[J].Int J Impact Eng,2005,31(1):55-83.

[12]Langdon G S,Chung Kim Yuen S,Nurick G N.Experimental and numerical studies on the response of quadrangular stiffened plates.Part II:Localised blast loading[J].Int J Impact Eng,2005,31(1):85-111.

[13]侯海量,朱錫,古美邦.爆炸載荷作用下加筋板的失效模式分析及結構優化設計[J].爆炸與沖擊,2007,27(1):26-33.

Hou Hailiang,Zhu Xi,Gu Meibang.Study on failure mode of stiffened plate and optimized design of structure subjected to blast load[J].Explosion and Shock Waves,2007,27(1):26-33.(in Chinese)

[14]Nurick G N,Langdon G S,Chi Y.Behaviour of sandwich panels subjected to intense air blast-Part 1:Experiments[J]. Comp Struct,2009,91:433-441.

[15]Xue Z,Hutchinson J W.A comparative study of impulse-resistant metal sandwich plates[J].Int J Impact Eng,2004,30 (10):1283-1305.

[16]Zhu F,Zhao L M,Lu G X,et al.A numerical simulation of the blast impact of square metallic sandwich panels[J].Int J Impact Eng,2009,36(5):687-699.

[17]陳長海,朱錫,侯海量等.近距空爆載荷作用下雙層防爆艙壁結構抗爆性能仿真分析[J].海軍工程大學學報, 2012,24(3):26-33.

Chen Changhai,Zhu Xi,Hou Hailiang,et al.Numerical analysis of blast resistance of double-layer bulkhead structures subjected to close-range air blast[J].Journal of Naval University of Engineering,2012,24(3):26-33.(in Chinese)

[18]陳長海,朱錫,侯海量等.近距空爆載荷作用下固支方板的變形及破壞模式[J].爆炸與沖擊,2012,32(4):368-375.

Chen Changhai,Zhu Xi,Hou Hailiang,et al.Deformation and failure modes of clamped square plates under close-range air blast loads[J].Explosion and Shock Waves,2012,32(4):368-375.(in Chinese)

[19]Vaziri A,Hutchinson J W.Metal sandwich plates subject to intense air shocks[J].Int J Solids Struct,2007,44(6):2021-2035.

[20]Kambouchev N,Noels L,Radovitzky R.Numerical simulation of the fluid-structure interaction between air blast waves and free-standing plates[J].Comput Struct,2007,85(11-14):923-931.

[21]白志海,蔣志剛,嚴波等.金屬加筋板局部爆炸沖擊荷載研究[J].振動與沖擊,2011,30(12):93-97,194.

Bai Zhihai,Jiang Zhigang,Yan Bo,et al.Localized blast loading of a stiffened metal plate[J].Journal of Vibration and Shock,2011,30(12):93-97,194.(in Chinese)

[22]Hanssen A G,Enstock L,Langseth M.Close-range blast loading of aluminium foam panels[J].Int J Impact Eng,2002, 27(6):593-618.

Numerical analysis of the blast-resistant mechanisms of multilayered thin plates under close-range air blast load

LIU Yan-honga,CHEN Chang-haib,ZHU Xib,LI Wanc,HOU Hai-liangb,TANG Tingb
(a.College of power engineering;b.Department of Naval Architecture Engineering;c.Department of Weapon Engineering,Naval University of Engineering,Wuhan 430033,China)

To explore the blast-resistant mechanisms of large-scale multilayered thin plates subjected to close-range explosions of warheads,finite element simulations as well as model tests were carried out.Blast loads,deformation processes,strain distributions and deformation energy absorptions of the clamped multilayered square plates under close-range air blast loads were numerically analyzed.Comparisons between multilayered plates and single-layer plates of the same materials and equal total thicknesses were conducted. On the basis of the numerical analysises,further investigations into the influences of interlayer spaces,layer numbers and boundary conditions on the blast resistances of multilayered plates were performed.The results show that under model test conditions,multilayered plates absorb more deformation energy than their monolithic counterparts,whereas their maximum strains are smaller,and strain distributions are more uniformly than those of the monolithic counterparts.Under ultimate strain conditions,a significant enhancement in deformation energy absorptions is obtained for multilayered plates comparing with their monolithic counterparts.Appropriate increase of interlayer spaces leads to a certain extent enhancement in deformation capabilities for multilayered plates,while overlarge interlayer spaces are unfavourable to their overallharmonious deformations.Deformation capabilities of multilayered plates are improved by increasing layer numbers.Comparing with clamped boundary conditions,simple-support boundary conditions are more conductive to the adequate exertion of deformation-energy-absorbing capabilities for multilayered plates.

explosion mechanics;close-range air blast load;multilayered thin plate; blast-resistant mechanism;numerical analysis

O344.7

A

10.3969/j.issn.1007-7294.2014.07.012

1007-7294（2014）07-0821-13

2014-05-04

國家自然科學基金項目（51179200，51209211）

劉燕紅（1970-），女，博士，海軍工程大學副教授，E-mail：LIUyhhg502@126.com；

陳長海（1985-），男，海軍工程大學博士，講師，E-mail：chenchanghai0746@163.com。