結構外聲場的映射變階波包絡無限元法

蘇楠，龐福振，姚熊亮

結構外聲場的映射變階波包絡無限元法

蘇楠，龐福振，姚熊亮

（哈爾濱工程大學船舶工程學院，哈爾濱150001）

基于徑向形函數可任意變階的映射波包絡聲學無限元法，以無限長圓柱殼體為研究對象，用數值計算方法對其結構外聲場進行研究分析，并與其解析解進行對比，結果表明：兩者之間能夠較好地吻合，從而驗證了映射變階波包絡聲學無限元法在計算結構聲輻射中的可行性，且具有效率高、精度好等優點。在此基礎上，本文還討論虛擬極點位置對聲輻射的影響，通過對比四極子極點偏心聲壓值發現：極點存在偏心時，對實際工程問題有不利影響，但隨聲學無限單元階數的增加，誤差會減小。

映射變階波包絡法；聲學無限元；虛擬極點；聲輻射

1 引言

計算結構外聲場問題可歸結為無界域聲波波動方程的數值求解問題，如水下航行器的聲輻射問題、機翼的流激噪聲等。有限元法在求解此類問題時，計算量大且效率不高，并會帶來較大的聲學截斷誤差。因此，為了克服有限元法在求解無限域結構外聲場問題時的不足，從而提出無限元法。

關于無限元法的相關問題研究國內外已有大量文獻發表，其中具有代表性有：Bettess和Zienkiewicz[1-2]在研究表面水波和折射問題時首次提出了無限元的概念，將聲學問題在無窮遠處滿足的解直接移植到人工邊界上；并針對無限元的不足提出了一種映射無限單元，通過單元建立了局部坐標系與整體坐標系的映射關系，但在求解過程中碰到了從未定義過的指數型積分，在數學上沒有嚴格的理論推導證明；Astley[3]依據Bettess[4]無限元思想提出了一種新的無限單元類型，這一單元類型中取權函數為形函數的復數共軛，運用Garlerkin加權殘值法求解，該方法徹底消除了單元矩陣中的不確定積分，極大地簡化了方程，而且系統矩陣中頻率與剛度矩陣相互獨立，從而可使用高斯積分對方程進行求解，后來此法被Cremers等人[5-7]將此聲學無限元法發展成為徑向方向可任意變階的映射波絡無限元法，并將幾何映射函數和形函數分開處理。楊瑞梁[8-12]對聲學無限元法的發展和研究進行了系統的闡述，同時對無限元法進行了詳細地分類，從理論上分析了收斂性、條件數和角向量數對計算精度的影響。

在上述研究的基礎上，本文基于徑向方向任意變階的映射波包絡聲學無限元法，較為詳細地推導了系統矩陣平衡方程，并與解析法進行對比，驗證了映射變階波包絡聲學無限元法求解結構外聲場的可行性，在此基礎上，著重分析了虛擬極點偏心對聲輻射計算精度的影響。

2 映射變階波包絡聲學無限元法

本文基于徑向形函數可任意變階的聲學無限元法，形函數沿兩個方向相互獨立構造：在徑向上，采用任意階數的拉格朗日多項式，從而實現了徑向形函數的任意變階；在橫向上，保持形函數不變，這樣可實現與低階有限元的直接耦合。

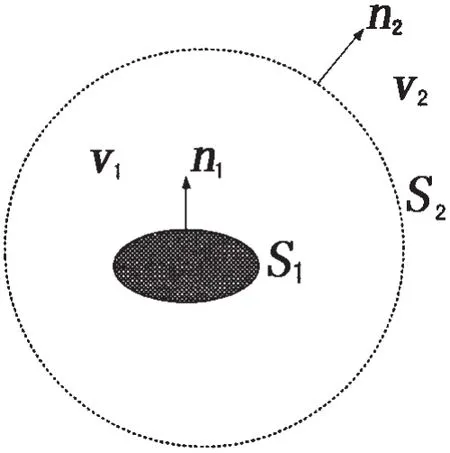
圖1 聲場幾何模型Fig.1 The geometry model of sound field

2.1 域內控制方程

考慮內邊界為S1的無限大區域V，如圖1所示。p（ x，t）為邊界S1上的法向聲壓，假設該聲波為一簡諧波，p（ x，t）可表示為p（ x，t）=p（x） eiwt，它在聲場域V內滿足以下波動方程：

式中：V為外部無界區域，k=w/c為聲學波數，▽2為拉普拉斯算子。在結構輻射表面S1應滿足以下邊界條件：

式中：U（）

x為法向振速。在無窮遠處應滿足Sommerfeld條件：

無限大外域聲場問題可歸結為求解邊值問題（1）-（4）。

2.2 方程離散

為求解邊值問題（1）-（4），引入較為簡單的人工邊界S2，將域V劃分為內部區域V1和外部區域V2。在區域V1內采用常規的有限元法離散；在區域V2內采用無限單元離散，無限單元為向無限遠延伸的四邊形，如圖2所示。此無限單元由一正方形母單元映射而來，節點1和2位于人工邊界S2上，節點

式中：r為整體坐標系中坐標原點到區域V內一點的距離。

如果在遠場邊界S2上，S2距離振動體足夠遠，等效近似有限聲學邊界條件為：1、2、3、4分別對應母單元中的四個節點，其他兩節點（1，1）和（1，-1）映射到無限單元的無窮遠處。節點1′、2′與節點3、4關于節點1、2鏡像。從局部坐標系ζ-ξ到整體坐標系x-y的映射函數為：

圖2 映射波包絡單元Fig.2 Mapped wave envelope element

式中：

沿著邊1-3和邊2-4的幾何映射關系式可以表示為：

式中：r為沿1-3或2-4邊距聲源點1′或2′測得的距離。

2.3 單元系統矩陣

記Wi為權函數，Ni為形函數，對Helmholtz方程（1）應用Glerkin加權殘值法，將在V上的體積分轉化為在S1和S2上的面積分，得到等效的Helmholtz方程為：

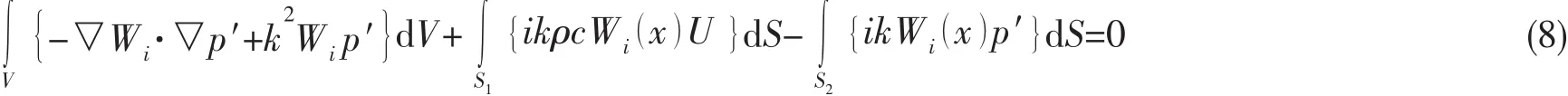
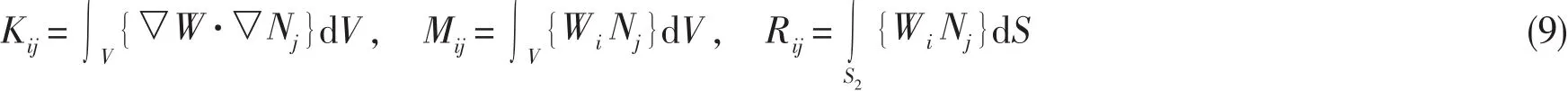
同時，聲學載荷量可以寫成：

那么，系數qi表達式可以通過方程式｛q｝=（［K］+ik［R］-k2［M ］）-1｛F｝求出，其中：｛q｝為節點聲壓列向量，［K］為剛度矩陣，［R］為阻尼矩陣，［M］為質量矩陣，｛F｝為載荷向量列矩陣，k為聲學波數。

形函數及權函數選取方法具體參考文獻[6]。對于圖2中的二維單元，各點的聲壓是基于幾何節點1和2的聲壓值線性插值求得。波包絡無限單元的插值函數Ni，其中包括模擬幅值衰減部分和聲場中聲壓相位變化部分。對于n階波包絡法中僅考慮各自形函數下n個節點的聲壓，并認為第（n+1）個節點的聲壓值在無窮遠處為零。

母單元中n階多項式形函數采用拉格朗日多項式求得，其中n階拉格朗日多項式由分列在幾何節點之間的n個聲學節點確定。n階徑向形函數可表示為：

通過使用局部映射函數ζ=ζ1+τh=τ/（n-1）-1，其中h=1/（n-1）。當ζ1=-1時，徑向形函數可寫成以下形式：

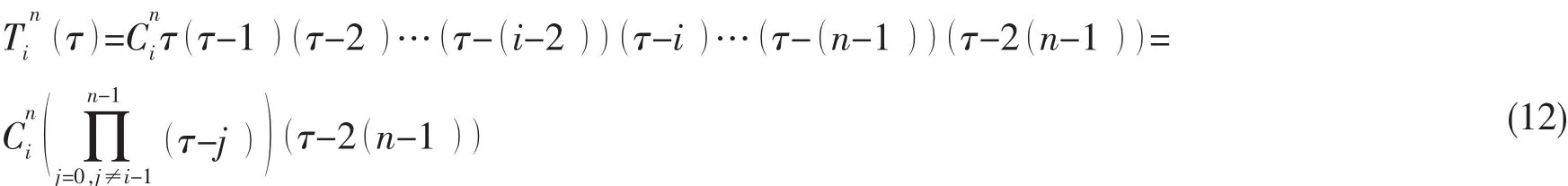
在母單元中使用此徑向形函數映射到實際單元中為1/r的展開式，它適用于模擬三維或軸對稱聲波傳播中的幅值衰減問題。但在二維聲學問題中，聲波幅值近似以形式衰減。對于二維問題，它的徑向形函數由乘以系數因子相當于在母單元中乘以相應系數項。此時，二維徑向形函數可以表示為：

在形函數中引入形如e-ikr的周期分量描述波形相位變化。為保證聲學單元的連續性，在有限單元與無限單元的交界面ζ=-1處相位必須設定為零。因此，在局部坐標系中，相位變化可描述為：在二維聲學無限單元中橫向形函數可采用線性單元，不同邊界對應的形函數為（如圖2所示）：

相位函數μ（ ξ，ζ）可由極點位置a（ξ）插值得到，a（ξ）為如下表式：

從（16）式中可看出，向外傳播的行進波是由在近場中的虛擬極點發散出來的，虛擬極點位于有限單元與無界單元的交界面a（）ξ處。將模擬聲壓幅值衰減函數和相位變化函數結合起來，給出n階聲學單元的形函數如下：

波包絡法中權函數取為形函數的復數共軛乘以一加權因子（a/r）2，能保證無限單元中的剛度陣和質量矩陣的積分有限，同時能夠滿足無窮遠處輻射條件。故權函數的表達式為：

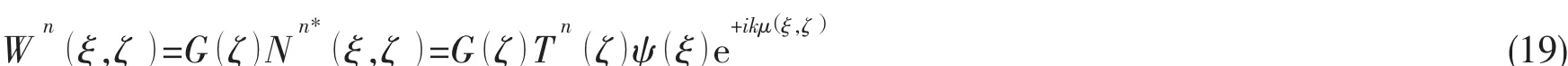
其中幾何權函數加權因子在局部坐標系中可表示為：

基于文獻[6]可得到二維n階無限波包絡單元的剛度矩陣和質量矩陣的系數分別為：

單元矩陣中，復雜指數形式在被積函數中已被消除，故可采用數值高斯積分得到各個單元矩陣中的系數。單元矩陣中的各項系數經過組裝得到系統矩陣，帶入系統平衡方程即可求解得到所求節點聲壓值。

3 數值計算

3.1 映射變階波包絡聲學無限元法有效性驗證

基于映射變階波包絡聲學無限元法理論，求解聲壓計算框圖實現步驟見圖3。為滿足調整單元階數的靈活性，即通過增加徑向節點數目來實現聲學無限映射單元中徑向形函數的任意變階。然而，母單元中任意增加節點數，必須保證映射到實際單元中時是沿著無窮遠邊界發散的，絕對不能出現交叉現象，即不存在當ζ∈[-1，1）時，通過方程（7）得到點的坐標不能位于1-4或2-3連線上。n階聲學映射無限元單元的位置是由它的四個幾何節點和n階徑向插值形函數確定。在n階無限單元徑向上至少需要（n+1）個高斯積分點，橫向方向上至少需要3個高斯積分點才能滿足計算精度要求。

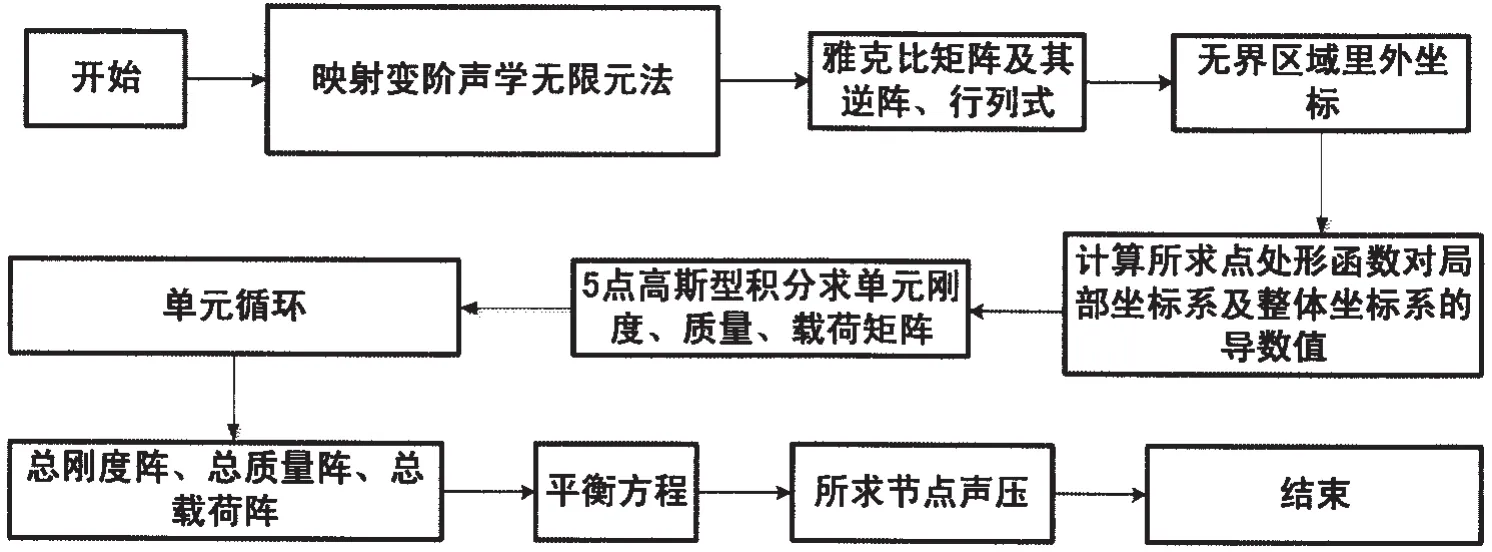
圖3 無限元聲壓矩陣計算框圖Fig.3 Acoustic infinite element pressure matrix computation block diagram

本文基于映射變階波包絡聲學無限元法通過數值計算給出三維無限長剛性體運動的聲輻射。取浸沒在無限域流場的一個二維軸對稱無限長圓柱殼體為研究對象，計算求解無限聲場域中聲壓。將數值計算結果與文獻[6]解析解對比來驗證本文方法的有效性。以下所有算例中，聲學介質密度為ρ= 1 024 kg/m3，聲傳播速度為c=1 500 m/s，如不作特殊說明，這些參數保持不變。

3.1.1 解析解

二維單極子、偶極子和四極子在柱坐標系中的聲輻射解析解可表示為：

其中：V0為振速幅值，V0=1e-6 m/s。

3.1.2 數值解

在無量綱化參數ka=π a=1（）m下，偶極子、四極子聲輻射在聲場中的聲壓分布圖如圖4、圖5所示。確定聲學波數k使圓柱體直徑2a對應一個波長。法向速度邊界條件V0=1e-6 m/s。

由圖4可知，通過將偶極子聲輻射數值解與解析解對比發現二者吻合程度很好且計算效率高；隨著波包絡單元階數提高，誤差變得更小。由此可判定聲學無限元方法能夠很好地滿足計算精度要求。

其中：Hn為第二類n階漢克爾函數，n=0，1，2分別對應單極子、偶極子和四極子聲輻射。

在無限長圓柱體振動表面的法向速度分布為：

圖4 振動圓柱體輻射聲壓（ka=π）-+-+-，解析解；-o-o-，數值解Fig.4 The radiated sound pressure of vibration cylinder(ka=π).-+-+-,analytical solution;-o-o-,numerical solution

圖5 振動圓柱體輻射聲壓（ka=π）-o-o-，解析解；+*+*，數值解Fig.5 The radiated sound pressure of vibration cylinder(ka=π).-o-o-,analytical solution;+*+*,numerical solution

由圖5可知，通過將四極子聲輻射數值解與解析解對比發現二者吻合程度也很好；同時發現徑向形函數的階數越高，二者的吻合程度相當高。從偶極子和四極子算例中，分析發現將映射變階波包絡聲學無限元法應用到求解結構外聲場聲壓是可行的，且具有較高的精度。

3.2 虛擬極點位置對結構聲輻射的影響

在映射波包絡無限元法中，假設了一個在物理意義上不存在的虛擬聲源（即極點），其中極點作為聲源的擾動起點具有重要作用。一般來說，虛擬極點聲源都放置在幾何中心處，恰似結構的輻射聲波從虛擬極點發出，但在實際工程問題中，很難滿足這樣的要求。因此有必要討論虛擬極點位置對結構聲輻射的影響。本節以簡單聲源（四極子）為例分析了虛擬極點位置對聲輻射的影響。

在無量綱常數ka=π a=1（）m下，極點偏心距離取X=-0.5 m時，四極子聲學無限元聲輻射虛擬極點偏心與未偏心數值解對比如圖6所示。

圖6 虛擬極點位置對輻射聲壓的影響（ka=π）-+-+-，虛擬極點未偏心；-o-o-，虛擬極點偏心數值解Fig.6 The virtual sound source’s position influence on radiated sound pressure(ka=π).-+-+-,virtual sound source in center;-o-o-,numerical solution of virtual sound source with decentration

如圖6所示，虛擬極點的位置不同對輻射聲壓的影響不同，通過對比四極子極點偏心聲壓值發現，當虛擬極點存在偏心時，對聲壓計算精度有不利影響。但隨聲學無限單元的階數增加，誤差會變小，其數值解會接近于真實解。因此，在實際工程問題中應增加聲學無限單元的階數來提高計算精度，控制虛擬極點的偏心距離來減小誤差。

4 結論

本文基于映射變階波包絡聲學無限元法，以無限長圓柱殼體為研究對象，將映射型聲學無限元法與有限元法耦合求解無界域遠場的輻射聲壓，提出了結構近場可用有限元模擬，遠場可用聲學無限元法離散的模型，運用映射型聲學無限元法數值求解了研究對象的聲輻射，與解析解對比驗證了映射變階波包絡法的有效性，并進一步討論虛擬極點位置對聲輻射的影響。結論如下：

（1）在無限流場域中具有法向振速的結構外取一簡單的人工邊界，在人工邊界內采用有限元離散求解邊界節點信息，而在人工邊界外敷設一層聲學無限單元，在無限單元中通過耦合邊界節點信息，從而采用徑向映射變階的波包絡無限元法求解遠場輻射聲壓。

（2）基于映射波包絡無限元法的理論，通過數值計算對比驗證了映射變階波包絡聲學無限元法在計算結構外聲場聲壓的有效性，分析發現映射變階波包絡聲學無限元法具有較高的計算精度及求解效率；

（3）虛擬極點偏心對聲輻射計算精度有較大影響，因此在實際工程問題中，應增加聲學無限單元的階數來滿足計算精度要求，同時也要控制減小虛擬極點的偏心距離。

[1]Burnett D S.A three-dimensional acoustic Infinite Element based on a prolate spheroidal multipole expansion[J].Acoust. Sot.Am,1996.

[2]Bettess P.Infinite Elements[M].Penshaw,Sunderland,U.K,1992.

[3]Astley R J,Eversman W.Wave envelope elements for acoustical radiation in inhomogeneous media[J].Computers and Structures,1988,30(4):801-810.

[4]Burnett D S,Holford R L Prolate and oblate spheroidal acoustic infinite element[J].Comput.Methods.Appl.Mech.Engrg, 1998,158:117-141.

[5]Tsynkov S V.Numerical solution of problems on unbounded domains[J].A Review Applied Numerical Mathematics,1998, 27:465-532.

[6]Cremers L,Fyfe K R,Coyette J P.A variable order infinite acoustic wave envelope element[J].Sound Vib,1994,171 (114).

[7]Cremers L,Fyfe K R.On the use of variable order infinite wave envelope element for acoustic radiation and scattering[J]. Acoust.Soc.Am.,1995,97(4):2028-2040.

[8]楊瑞梁,汪鴻振.聲無限元進展[J].機械工程學報,2003,39(11):82-87.

[9]楊瑞梁.聲學無限元法的研究[D].上海:上海交通大學,2004.

[10]楊瑞梁,汪鴻振.聲無限元進展[J].機械工程學報,2003,39(11):82-87.

[11]楊瑞梁,范曉偉.使用有限元和無限元耦合求解聲輻射問題[J].振動工程學報,2004,17:1007-1009.

[12]楊瑞梁,汪鴻振.用長旋轉橢球函數重構聲場[J].噪聲與振動控制,2003,5:15-17.

Variable order mapped wave envelope element of outer structural sound field

SU Nan,PANG Fu-zhen,YAO Xiong-liang
(Harbin Engineering University,Harbin 150001,China)

This paper is on the basis of a variable order in radial direction infinite acoustic wave envelope element(WEE).Numerical method is adopted to study the sound radiation pressure of an infinitely long cylinder as the subject investigated,and obtained results agree well with analytic solutions.The research presents that the variable order infinite acoustic wave envelope element which can be successfully applied to sound radiation pressure computation field is proven.The WEE has obvious advantages such as high efficiency and high degree of accuracy.Based on the above results,this paper also describes the influence of virtual sound source’s location in sound radiation,and it can be concluded that the decentration of virtual source has bad effects on the actual project by comparing the sound pressure values of quadrapole.However,with the increased orders of infinite acoustic element,the inaccuracy of sound pressure is decreasing.

variable order mapped wave envelope elements;infinite acoustic element; virtual sound source;sound radiation

O42

A

10.3969/j.issn.1007-7294.2014.07.016

1007-7294（2014）07-0856-08

2014-03-02

國家自然科學基金項目（51209052）；黑龍江省青年科學基金資助項目（QC2011C013）；哈爾濱市

科技創新人才研究專項資金項目（2011RFQXG021）；國防預研重點項目（401040XXX0103）

蘇楠（1976-），女，碩士研究生，E-mail：sulanlan1988@126.com；

龐福振（1981-），男，博士，哈爾濱工程大學副教授。