通過集體備課確立圓錐曲線二輪復習思路

■張戀

通過集體備課確立圓錐曲線二輪復習思路

■張戀

今天的集體備課，我們研討的主題是：通過對前一階段學生圓錐曲線學習的學情分析，針對學生出現的問題，討論一下下一階段各層次班級圓錐曲線二輪復習的教學方案。

一、高考對圓錐曲線的要求

從圓錐曲線練習卷來分析，這份試卷的選題主要以圓錐曲線的基礎題和中檔題為主，內容覆蓋了高考對圓錐曲線考查的兩個方面：

1.客觀題重點考查圓錐曲線的定義及應用；圓錐曲線的標準方程；圓錐曲線的基本量（a、b、c、e、p等），還有離心率等問題。

2.解答題考查的是：求圓錐曲線的方程和軌跡方程；圓錐曲線的的幾何性質；直線與圓錐曲線的位置關系；范圍、最值問題。

二、學情調查情況及反饋

每位老師通過批改學生試卷，對各班學生解題出現的問題進行收集，由詹老師、高老師和我將學生出錯較多的試題及解答的錯誤，挑選出比較典型的錯誤以及個別大題解法作了一個對比，由何老師制作成表格，現在通過投影呈現部分學生的試卷，來進行反饋和反思。

例如，第14題的主要問題表現在，一是學生求軌跡方程時方法選擇不當，二是學生對雙曲線的定義把握不準確。

14.求與圓（x+2）2+y2=2外切，并且過定點B（2，0）的動圓圓心M的軌跡方程。

例如第17題主要問題表現在，一是學生不知道條件“為銳角”如何轉換，二是轉化為余弦定理，計算量較大，三是沒有注意Δ>0的限制。

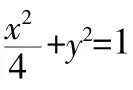
（2）設過定點M（0，2）的直線l與橢圓交于不同的兩點A，B，且∠AOB為銳角（其中O為原點），求直線l的斜率k的取值范圍。

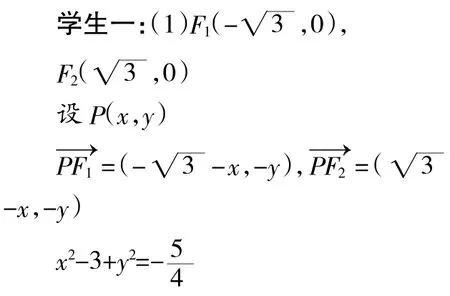
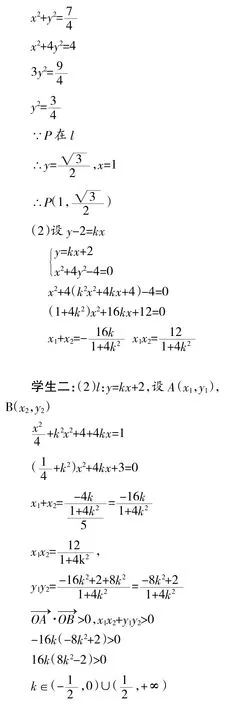
我們幾位老師一起總結了一下學生在學習圓錐曲線主要反映出來的問題，有如下幾點：

1.對基礎知識的理解不扎實，不會應用，其根本原因是學生數學思想欠缺。在基礎知識方面，同學們大多都停留在對公式、定理及推理的表面了解和熟悉上；例如解答題第14題不會靈活運用雙曲線的定義解題，計算繁瑣；用了定義的同學又是一知半解，不注意定義中強調的“差的絕對值”，而忽略了范圍。

2.對圓錐曲線與平面向量的結合，不會將條件轉化為坐標關系。例如第15（2）、17（2）題，從而造成方法選擇不當，思維混亂。

3.對求離心率e取值范圍的問題，不會將a、b、c之間的等量關系與不等式關系聯系起來，例如第8、第11題。這說明學生在方程與不等式的數學思想、等價轉化的數學思想等能力不強。

4.不仔細分析題目，對直線方程的選取沒有優化，容易忘記對斜率不存在情況的討論，以及對△不進行判斷，就直接出現韋達定理的結果。

5.解析幾何對學生來說最大的困難在于運算量大。學生往往能形成思路，但解題過程當中也會因為運算問題常常被卡住，算不出正確結果來。這體現出學生的基本運算訓練沒有落實，以及學生對算法、算理的理解和儲備不夠。

三、后階段復習的策略與建議

針對以上問題，我認為文理各層次班級，在二輪復習圓錐曲線中的側重點應有不同，普通班不能完全采取放棄的策略，不重視對解析幾何的復習；中間層次的班級也不應放棄一些在能力范圍內的題，爭取大題中的第2問能動筆；火箭班中的絕大部分同學應力爭解析幾何大題得10分以上。所以，結合我們這次的學情調查暴露出來的問題，對后一階段的復習，可采用以下幾點建議。

1.進一步強化概念，提高學生應用定義解題的意識。

2.強化數形結合。例如用待定系數法求圓錐曲線方程時，可以數形結合——先定型，再定量。

3.加強基本方法，典型題型的訓練。設而不求、整體代換、點差法這些基本方法必須熟練掌握，直線與曲線位置關系、定點、定值、范圍等問題必須熟練解題套路。審題時多收集信息，綜觀全局，權衡利弊，再決定解題策略。

4.突破運算關。直線與圓錐曲線的綜合問題一直是高考的熱點，解答的關鍵是坐標化，難點是代數運算和推理，以及參數的處理。而運算能力差是學生普遍存在的問題，課堂上老師要示范計算過程，給足時間讓學生自己算，在運算過程中，力求避繁就簡。平時教學中，教師要培養學生運算的求簡意識，突出解析幾何設而不求的運算本色，充分發揮圓錐曲線的定義和利用平面幾何知識化難為易、化繁為簡的作用。

5.提高學生等價轉化的能力。實現復雜問題簡單化、陌生問題熟悉化。例如教給學生一些常用的解答策略：①沒有圖形，不妨畫個圖形，以便直觀思考；②“設——列——驗”是求軌跡的通法；③消元轉化為一元二次函數（方程），判別式、韋達定理、中點、弦長公式等要把握好；④多感悟“設——列——解”，設什么？可以設坐標、方程、角、斜率、截距。列的前提是找關系，解就是轉化、化簡、變形，向目標靠攏；⑤緊扣題意，聯系圖形，數形結合。

6.指導學生對問題進行較深入的思考和橫向聯系。解析幾何可與集合、簡易邏輯、函數、方程、數列、三角、平面幾何、平面向量、不等式、導數等知識點融合；特別是與新增內容的綜合，如線性規劃與平面幾何的綜合，圓錐曲線與向量、導數的綜合問題，利用參數方程與極坐標解決圓錐曲線綜合問題等。

7.進一步強調表達的規范，解題步驟書寫合理（如在求直線方程中，一定要代入原方程進行檢驗）。

8.根據各班的實際情況有針對性地設立專題，如定義、性質的應用，范圍、最值問題，定點、定值問題，存在性問題等。

解析幾何題不但能體現考試說明中對運算能力的要求，還能很好地體現個性品質要求：考生要以平和的心態參加考試，合理支配考試時間，以實事求是的科學態度解答試題，樹立戰勝困難的信心，體現鍥而不舍的精神。

（作者單位：武漢市育才高級中學）

責任編輯 王愛民