基于組合預測模型的滾裝碼頭吞吐量預測

莫艷芳， 趙一飛

（1.上海交通大學中美物流研究院，上海 200030;2.上海交通大學安泰經濟與管理學院，上海 200030）

滾裝運輸以其專業性強、運輸批量大、破損率小、運費低、污染低等優勢吸引著汽車經銷商。為滿足我國汽車銷售市場不斷增長的需要，滾裝碼頭的發展正呈現出巨大的需求。為適應這一需求，交通運輸部于2006年批準大連、天津、上海和廣州四港的滾裝碼頭成為我國進出口整車的指定口岸，極大地推動了這四個港口滾裝碼頭的發展。2006—2011年，這四個港口的吞吐量如表1所示，可見其波動性大，規律不明顯。為正確引導我國滾裝碼頭的建設，為滾裝運輸提供必要的基礎設施，有必要對滾裝碼頭吞吐量的預測方法進行研究。

表1 四大滾裝碼頭內貿整車吞吐量 單位:輛

港口貨物吞吐量的預測方法［1－2］研究已經相當成熟，分貨種方面比較常見的是對港口集裝箱吞吐量預測方法［3－4］的研究。我國汽車滾裝運輸起步較晚，學者們對滾裝碼頭的研究［5－6］主要集中在關于線路優化或者船型設計等，對于滾裝碼頭吞吐量預測的研究相對較少。本文在對我國四大滾裝碼頭2006年以來開展業務的情況進行數據采集的基礎上，對滾裝碼頭發展趨勢及吞吐量的預測方法進行研究，試圖發現能反映滾裝碼頭發展特點的吞吐量預測方法。

一、一般預測方法及其應用

一般而言，港口吞吐量的預測方法主要有時間序列預測法、灰色模型預測法和相關性分析預測法等，以下分別將三種方法運用在上海港滾裝碼頭上，考察比較其預測精度。

（一）時間序列預測及應用

時間序列預測方法是以時間為自變量、預測值為因變量的預測模型，通過模型可以得到時間與預測值之間的關系，常用模型有指數函數、對數函數、冪函數、多項式等。把表1中上海滾裝碼頭吞吐量數據作為樣本處理分析發現，三次函數的擬合度最好，R2=0.981，通過檢驗，如式（1）所示。

基于該模型，擬合值與實際值的對比如表2所示。

表2 基于時間序列模型的實際值與擬合值對比 單位:輛

擬合情況如圖1所示。

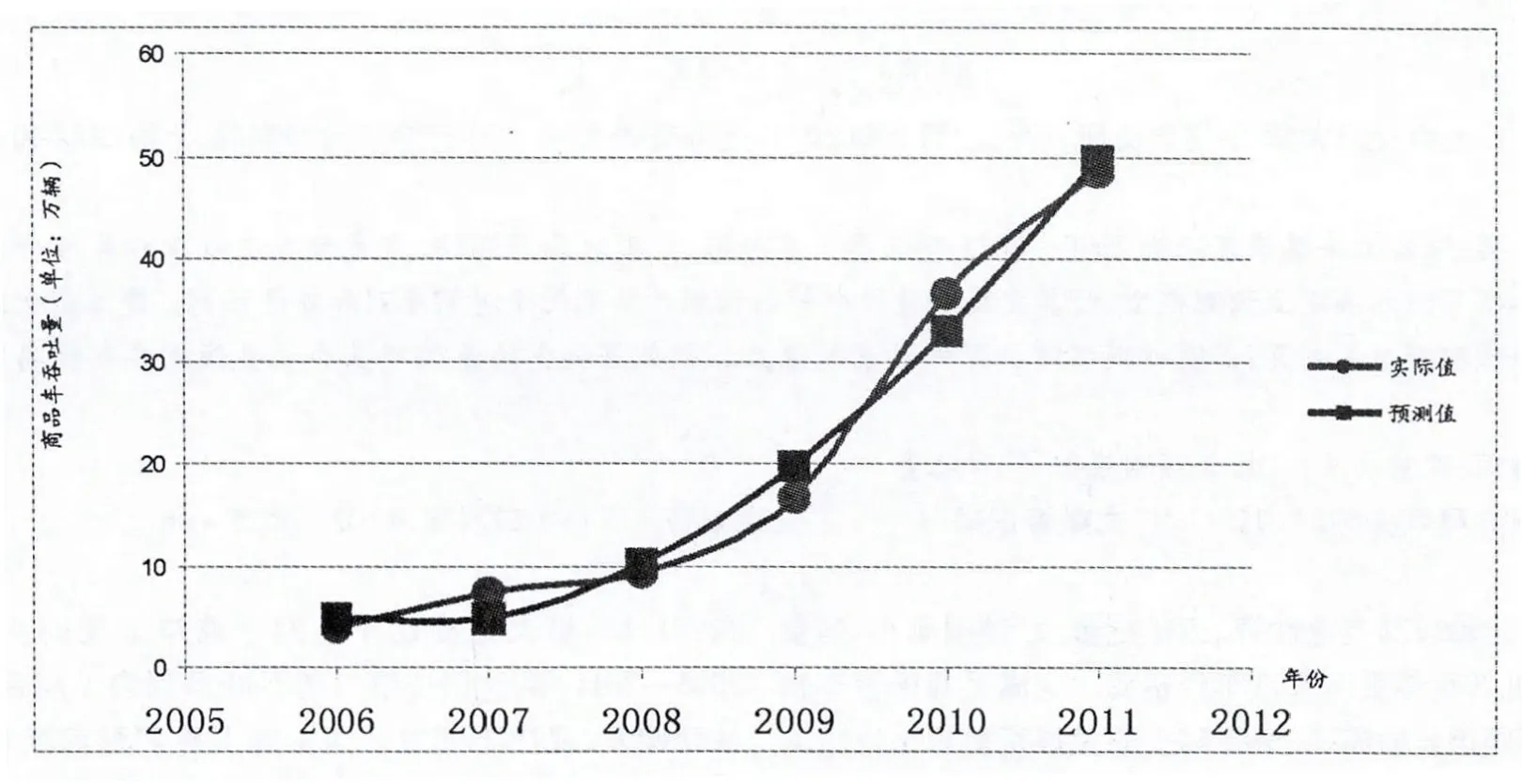
圖1 基于時間序列預測的擬合圖

（二）灰色模型預測及應用

鄧聚龍教授提出的灰色系統理論［7］具有能夠利用“較少數據”建模并發現趨勢的良好特性，克服資料不足或系統周期短的矛盾，對于目前樣本較少的滾裝碼頭吞吐量預測具有較好的適用性。GM（1，1）模型則是灰色系統法中應用最普通的一種預測方法，其得到模型時間序列的一階微分方程。

根據GM（1，1）的計算步驟進行建模，由表1上海港數據，可得到原始數據數列式（2）。

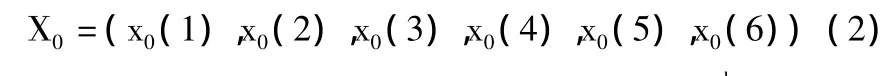
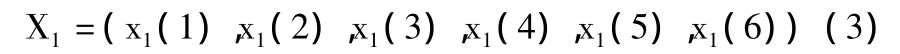
對于上述X0的GM（1，1）中的參數a和u，按式（4）進行辨識。

式（4）中的B和yn分別為式（5）和式（6）。

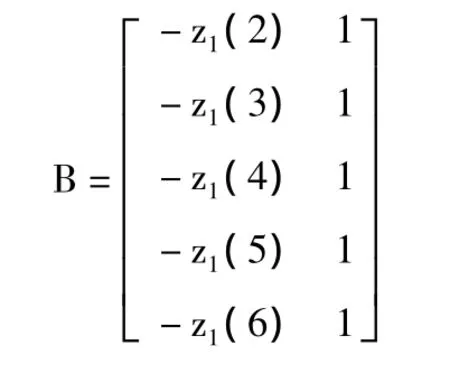
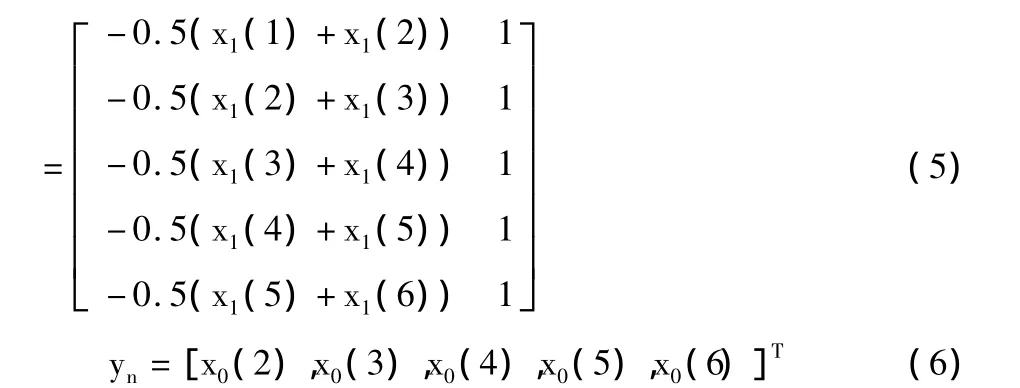
計算出a和u后，得到GM（1，1）模型的累加數列X1的灰色模型，如式（7）所示。

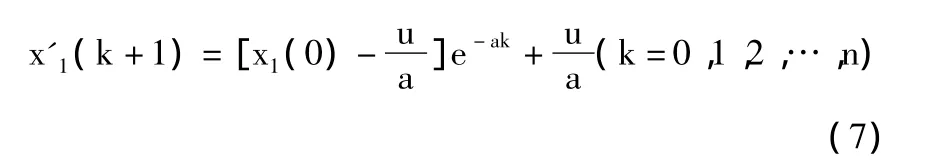
由此得到實際值與模型擬合值的比較，如表3所示。2006年的擬合值x'0（1）=x0（1）=39826，計算得到后驗差比值 C=0.013 ＜0.35，小誤差概論 P=0.986 ＞0.95。由此可知屬于一級精度，擬合效果很好。

（三）相關性分析預測及應用

相關性分析就是對兩個或多個具備相關性的變量元素進行分析，衡量變量因素的相關密切程度。滾裝碼頭吞吐量易受國內外政策、經濟、文化等因素的影響而波動，相關性分析可以將這些因素與吞吐量聯系起來，使預測分析更具科學性。

本文選定的是上海市GDP、汽車制造業工業總產值、

由式（7）累減還原，得到x0的灰色模型式（8）。民用車輛擁有量以及上海市人口密度四個因素作為自變量，進行相關性分析，這四個自變量可以科學衡量上海地區的汽車制造量和消費量。通過對歷年的《上海統計年鑒》整理可得到表4。

表3 基于灰色模型的實際值與擬合值對比 單位:輛

擬合情況如圖2所示。

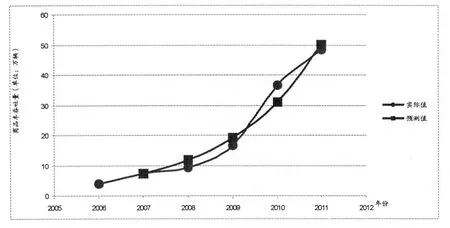
圖2 基于灰色模型預測的擬合圖

表4 相關性分析數據整理

采用SPSS中的相關性分析軟件，可得到上海港滾裝碼頭吞吐量和上海市GDP、汽車制造業總產值、民用車輛擁有量及上海港貨物吞吐量的Pearson相關性和雙側顯著性，如表5所示。

表5 相關性分析結果

通過表5可以看出，上海港滾裝碼頭吞吐量和上海市 GDP、汽車制造業工業總產值、民用車輛擁有量以及上海市人口密度屬于高度相關，四個自變量間存在高度相關性，建立多元回歸模型，回歸結果如表6所示。

表6 模型匯總表

R2高達0.998，說明自變量可以解釋因變量變化的99.8%。從表7的方差分析表可以看出，回歸平方和解釋了總平方和的很大部分，F 統計量為 145.338，Sig.＞0.05，差異顯著。

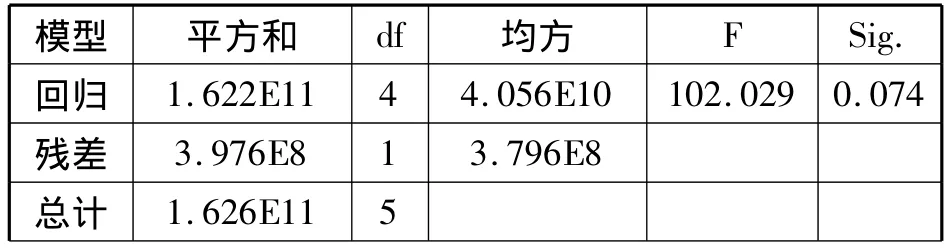
表7 方差分析表

表8是模型的參數表。

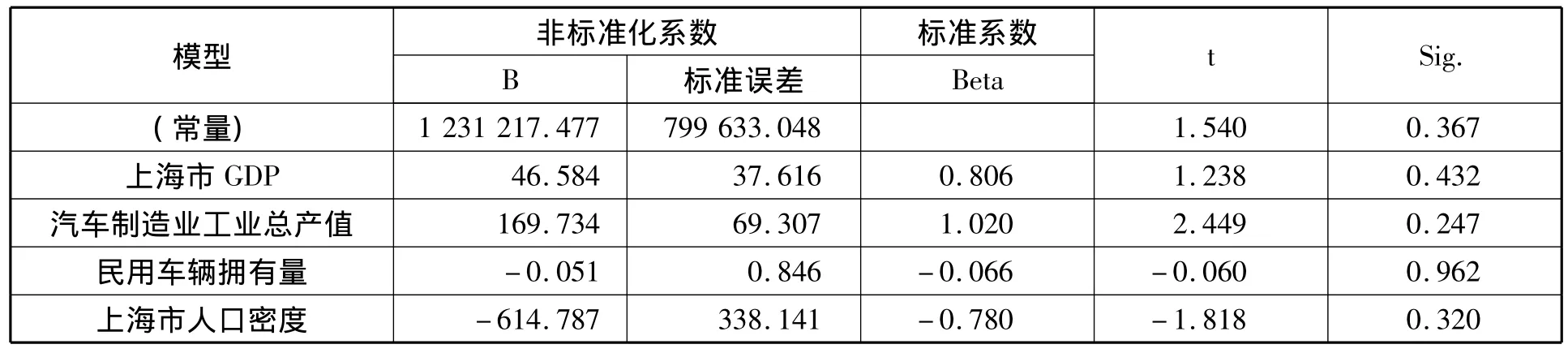
表8 模型參數表

用Y表示上海港滾裝碼頭吞吐量，X1、X2、X3和X4分別表示上海市GDP、汽車制造業工業總產值、民用車輛擁有量以及上海市人口密度，則得到多元回歸模型式（9）。

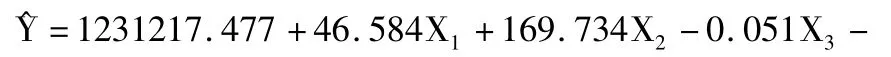
表9是通過多元回歸模型得到擬合值與實際值的對比。

表9 基于相關性分析的實際值與擬合值對比 單位:輛

擬合情況如圖3所示。

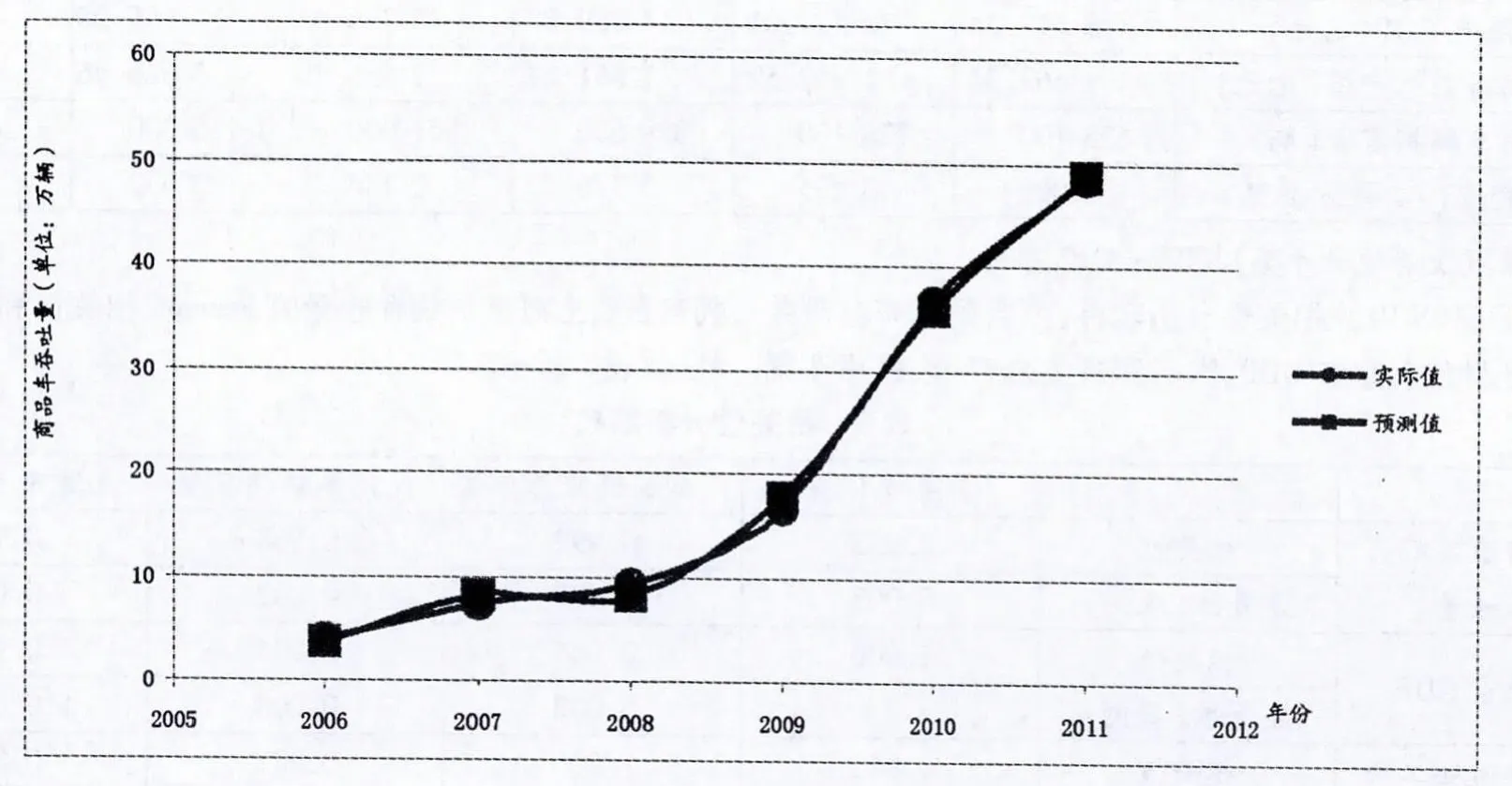
圖3 基于相關性分析預測的擬合圖

通過表10可以發現，相關性分析的擬合度比時間序列和灰色模型高，說明在考察滾裝碼頭吞吐量時將港口城市的經濟、人口等因素納入考慮范圍不無道理。

二、組合預測模型方法及其應用

（一）組合預測模型

自1969年組合預測思想［8］首次提出以來，一直是預測學界熱門問題之一，它可以彌補單個預測模型的片面性，通過利用不同模型的優點，賦予合適權重，大大提高預測的精度。

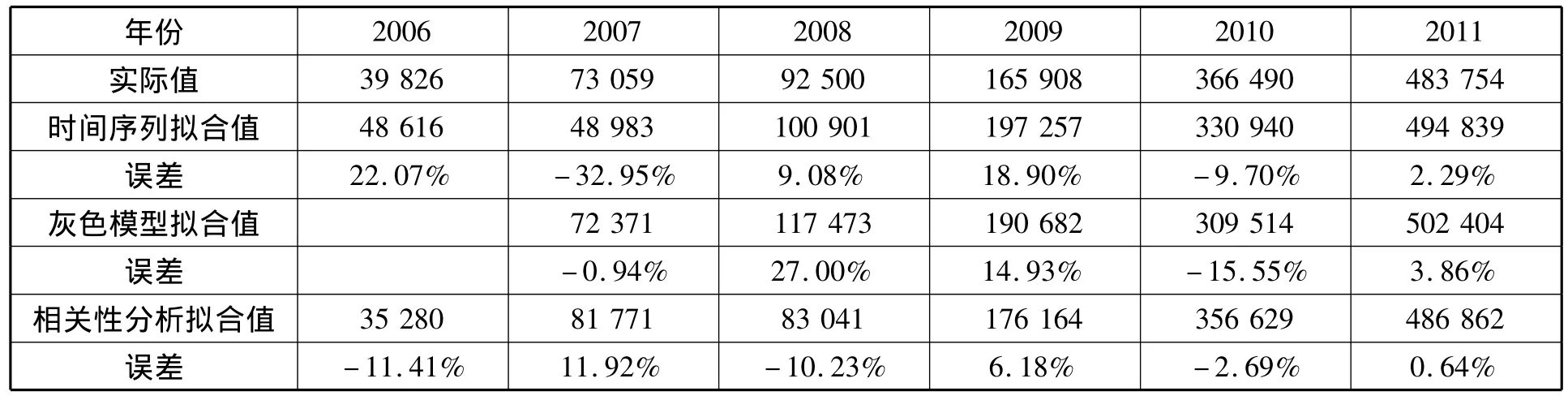
表10 時間序列、灰色預測與相關性分析的擬合值對比

本文采用的是以預測誤差平方和達到最小的線性組合預測模型［9］。設某一預測問題在某一時刻的實際值為yt（t=1，2，…，n），有k種可行的單項預測方法，其預測值分別為 yit（i=1，2，…，k，t=1，2，…，n），k 種單項預測方法的加權向量為 W=（ω1，ω2，…，ωk），設 y't= ω1y1t+ω2y2t+…+ωkykt是yt的組合預測值，于是以預測誤差平方和為準則的線性組合預測模型可通過式（10）求解。

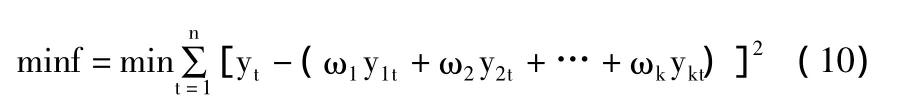
（二）組合預測模型的應用［10－15］

設ω1為時間序列擬合值在組合預測中的權數，ω2為灰色模型擬合值在組合預測中的權數，ω3為相關性分析模型擬合值在組合預測中的權數。通過組合預測模型，可以計算得出權數 W=（ω1，ω2，ω3）=（0.07，0.01，0.92）。

表11展示組合預測模型的擬合值與實際值的對比。

表11 基于組合預測模型的擬合值與實際值對比 單位:輛

組合預測模型的擬合圖如圖4所示。

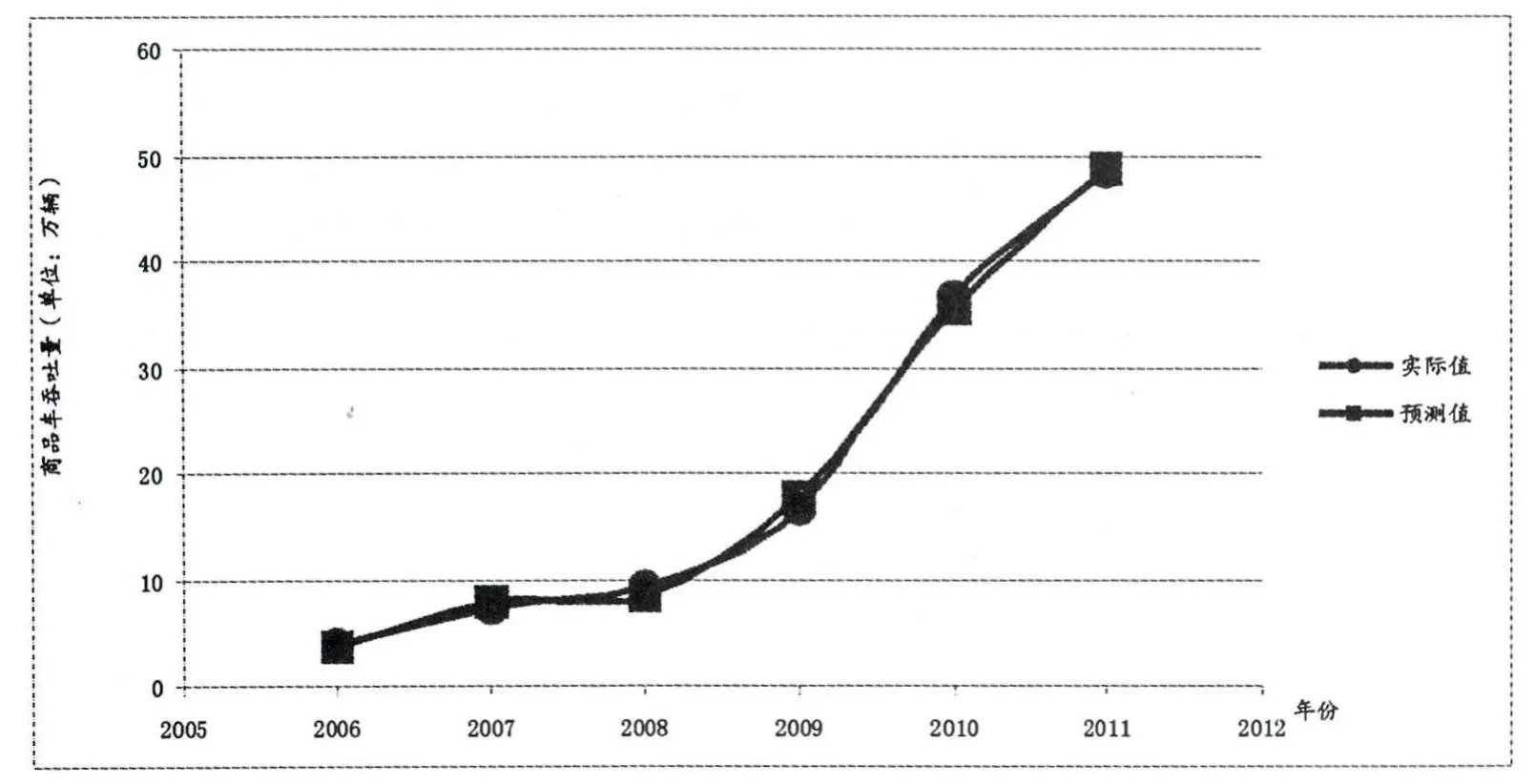
圖4 基于組合預測模型的擬合圖

可見，基于組合預測模型，上海港滾裝碼頭吞吐量的擬合度比之前三個單項方法都高，進一步證明了組合預測模型具有很好的精度和適用性。

三、結語

根據以上組合預測模型的研究，可以得到如下結論:自從被指定為整車進出口岸以后，上海港滾裝碼頭整體的吞吐量呈爆炸式增長，漲幅波動比較大，聯動內貿吞吐量迅猛發展。但可以肯定的是，未來的吞吐量規模將繼續保持增長的態勢。

上文的預測分析中分別用到了時間序列預測法、灰色系統預測法以及相關分析法。每一種預測方法擬合度都相當理想，但每種預測方法的使用條件不盡相同，如果只單純通過某一種特定的方法來預測，不可避免會帶來片面性。組合預測模型綜合了不同方法的優點，提高了預測的精度，可以推廣應用于更多規律性不明顯且影響因素復雜的數據預測。

本文需要改進的是預測時僅僅考慮到需求增長的可能，沒有將碼頭自身的作業能力和后方作業區的能力等供給因素作為約束條件，希望能在后續研究中加以考慮。

［1］劉明維，王多銀，周世良，等.港口貨物吞吐量預測方法探討［J］.水運工程，2005（3）:53－56.

［2］王紅雙，張欣蕾，朱榮艷.BP神經網絡在防城港貨物吞吐量預測中的應用［J］.物流科技，2010（5）:33－35.

［3］翟希東.港口集裝箱吞吐量預測模型研究［D］.大連:大連理工大學，2006.

［4］劉柱.灰色理論在港口集裝箱吞吐量預測中的應用［D］.合肥:合肥工業大學，2009.

［5］楊丹.多掛靠港的商品車滾裝船配載優化［D］.大連:大連海事大學，2012.

［6］陳丹.長江商品汽車滾裝運輸船船型開發研究［D］.武漢:武漢理工大學，2008.

［7］鄧聚龍.灰色系統基本方法［M］.武漢:華中科技大學出版社，2005.

［8］Bates J M，Granger C W J.The combination of forecasts［J］.Operational Research Quarterly，1969，20（4）:451－468.

［9］孫文一.中國汽車滾裝船運輸市場分析［J］.世界海運，2007，30（6）:9－11.

［10］郭宇.我國港口汽車滾裝專用碼頭發展現狀與展望［J］.中國港口，2009（1）:41－43.

［11］王嬌.幾種組合預測方法研究及其應用［D］.銀川:寧夏大學，2012.

［12］毛開翼.關于組合預測中的權重確定及應用［D］.成都:成都理工大學，2007.

［13］呂波，楊志軍，許淼.基于組合預測模型的世界海運周轉量預測分析［J］.中國造船，2012（2）:192－197.

［14］李躍旗，王穎.上海內河貨運量的組合預測［J］.中國航海，2009，32（4）:96－99.

［15］張盛.蘇北運河貨運量預測［J］.水運管理，2008，30（1）:8－12.