初中數(shù)學(xué)幾何圖形變化與分類案例分析

楊彥

【摘要】 初中數(shù)學(xué)中的幾何圖形教學(xué)具有很強(qiáng)的規(guī)律性，教師在授課時(shí)應(yīng)該根據(jù)圖形變化進(jìn)行分類討論，從而有助于學(xué)生更快更容易地理解和吸收知識(shí). 本文按照幾何形狀、圖形、位置的變化分類進(jìn)行討論，并且在教學(xué)課堂上不斷地慢慢深入，對圖形分類中出現(xiàn)的問題進(jìn)行分析和總結(jié).

【關(guān)鍵詞】 初中數(shù)學(xué)；幾何圖形；圖形變化；分類討論；分析

一、引 言

新課標(biāo)要求學(xué)生學(xué)習(xí)幾何知識(shí)時(shí)能從原來比較復(fù)雜的各類圖形分解出最基礎(chǔ)的圖形，要學(xué)會(huì)理解圖形中的各元素及圖形整體之間的關(guān)系，并根據(jù)最直觀的感覺來思考問題. 本節(jié)課是初中幾何數(shù)學(xué)一堂專門的復(fù)習(xí)課，教師根據(jù)學(xué)生平常考試和作業(yè)中涉及的、比較容易引起錯(cuò)誤的習(xí)題進(jìn)行歸類和討論，最后在教學(xué)課堂上講課時(shí)不斷地慢慢深入，對圖形分類中出現(xiàn)的問題進(jìn)行分析和總結(jié)，引導(dǎo)學(xué)生加深對幾何圖形的印象，并就根據(jù)什么規(guī)律如何分類進(jìn)行討論，從而把復(fù)雜的圖形題分類歸納成最基本的圖形，從而更有效地解決此類問題，培養(yǎng)學(xué)生敢于探索發(fā)現(xiàn)和創(chuàng)新的精神，以及求實(shí)、嚴(yán)謹(jǐn)?shù)目茖W(xué)態(tài)度. 本文列舉了三角形的周長問題、圓心距問題、圓的切線問題、復(fù)雜圖形證明問題四個(gè)方面，并舉例題來討論幾何圖形的變化與分類問題.

二、教學(xué)設(shè)計(jì)——圖形問題導(dǎo)入

在數(shù)學(xué)教學(xué)中，教師要引導(dǎo)學(xué)生對一些圖形進(jìn)行探討，對其中一些相同或是類似的圖形加以分析、對比、歸納及最后進(jìn)行總結(jié). 為此，在教學(xué)中的重點(diǎn)是教師要鼓勵(lì)學(xué)生充分利用和挖掘出日常生活中圖形變化的規(guī)律，并對造成這種現(xiàn)象和規(guī)律的原因分析探討，最后尋找這類圖形的相同點(diǎn)，那么學(xué)生解題就變得更加容易了. 例如，在初識(shí)幾何圖形的課堂中可以進(jìn)行如下方式導(dǎo)入：

T：同學(xué)們寫作業(yè)的時(shí)候用過方格紙作業(yè)本嗎？S（大家異口同聲）：用過.

T：大家有沒有注意觀察作業(yè)本的方格紙是什么形狀呢？我們現(xiàn)在投影儀屏幕上有一張作業(yè)本的方格紙（打出幻燈片），同學(xué)們看這個(gè)紙片是由什么樣的圖形組成的？S：由很多個(gè)小正方形組成.

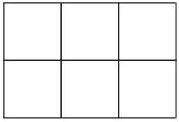
T：我拿出了其中的一部分（詳見圖1），我請同學(xué)們數(shù)一下投影儀屏幕上所示的正方形有多少個(gè)？S：共有8個(gè).

T：同學(xué)們你們是怎樣數(shù)出來的，而且是能保證正方形的個(gè)數(shù)不多不少？S：可以分成邊長為1和邊長為2的正方形，然后數(shù)數(shù)每種不同邊長的正方形分別有多少個(gè)，最后把這兩種正方形相加起來就可以了.

T：同學(xué)們講得很好，剛才這個(gè)方格紙的例子就是數(shù)學(xué)幾何中的簡單分類了，這就是對圖形的最基礎(chǔ)的分類討論.T：那么再數(shù)數(shù)看有幾個(gè)長方形呢？S：共有10個(gè)，可以把長方形分為三種，分別是寬為1，長為2；寬為1，長為3；寬為2，長為3，這三種類型的矩形，而后相加得出結(jié)果.

T：分類的標(biāo)準(zhǔn)應(yīng)該是統(tǒng)一規(guī)范的，既不能重復(fù)，也不能遺漏. （評：學(xué)生通過對簡單圖形的識(shí)別，體會(huì)分類討論的標(biāo)準(zhǔn)與原則，初步認(rèn)識(shí)到分類討論的必要性. ）

教學(xué)點(diǎn)評：此案例采用的是問題圖形導(dǎo)入法，首先在課堂上采用生活中常見的圖形來拋出問題，激發(fā)了學(xué)生對該幾何圖形的回想，不僅加深了學(xué)生對圖形印象，而且達(dá)到引起學(xué)生興趣的效果；然后拿出具體圖形讓學(xué)生進(jìn)行識(shí)別，同時(shí)導(dǎo)入分類討論的思想，不僅使學(xué)生易于理解，更在潛移默化中灌輸學(xué)生“分類討論”這種數(shù)學(xué)中非常有用的思想方法，從而達(dá)到事半功倍的效果.

三、案例教學(xué)

1. 三角形的周長問題

例1 已知一個(gè)三角形為等腰三角形，且它的兩條邊長分別是3厘米和5厘米，請問：這個(gè)三角形的周長是多少？

S：周長分別是11厘米和13厘米.

T：為什么會(huì)出現(xiàn)兩個(gè)答案呢？S：因?yàn)檫@個(gè)等腰三角形的兩條一樣長的腰長沒有確定下來，可以是腰長為3厘米，也可以是腰長為5厘米，所以最后結(jié)果不同.

T：同學(xué)們講得非常好，因?yàn)槿切蔚娜厸]有確定，所以三角形的形狀大小也會(huì)發(fā)生變化.

教學(xué)點(diǎn)評：在平時(shí)做題中學(xué)生經(jīng)常會(huì)犯“固定思維”的錯(cuò)誤，說到等腰三角形很多人只會(huì)把它固定到某一種，而實(shí)際中“腰長”和“底邊”并沒有確定下來，因此不管是“3”還是“5”都有可能是“腰長”或者“底邊”，但是此題也要考慮一種情況，如果兩條邊長分別是2厘米和5厘米，那么就只能有“腰長”是5厘米一種情況了，因?yàn)槿绻把L”是2厘米的話，那么另一“腰長”也為2厘米，此時(shí)“2 + 2 < 5”不符合三角形規(guī)律（三角形兩邊之和大于第三邊）.

2. 圓心距問題

例2 已知兩個(gè)圓的半徑分別為6厘米和9厘米，如果這兩個(gè)圓相切，那么圓心距為多少？

S：內(nèi)切是0，外切是15厘米.

T：為什么有兩種結(jié)果？S：因?yàn)閳D形的位置沒有確定，我們不知道兩個(gè)圓是內(nèi)切還是外切.

T：為什么要對幾何圖形進(jìn)行分類呢？那是因?yàn)椋?/p>

（1）幾何圖形形狀不唯一確定.

（2）幾何圖形位置不唯一確定.

教學(xué)點(diǎn)評：在解題中因?yàn)閹缀螆D形位置不唯一確定，而且?guī)缀螆D形形狀也不唯一確定，因此通過對幾何圖形的研究，使學(xué)生深刻理解對幾何圖形進(jìn)行分類的原因，同時(shí)通過對分類的原因進(jìn)行研究，初步學(xué)會(huì)怎樣進(jìn)行分類.

3. 圓的切線問題

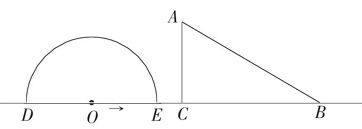
例3 如圖2，半圓O的直徑ED = 12厘米，△ABC中，已知∠ACB = 90°，∠ABC = 30°. 半圓以2厘米每秒的速度由左邊向右邊滑動(dòng)，在運(yùn)動(dòng)過程中，點(diǎn)D和點(diǎn)E始終都保持在直線CB上滑動(dòng)，假設(shè)運(yùn)動(dòng)時(shí)間為t，且已知OC = 8厘米. 試問：當(dāng)t為何值時(shí)，△ABC一邊所在直線與半圓O所在的圓相切？

T：兩種圖形保持相切的關(guān)系有哪幾種？

S：有四種關(guān)系，分別是線段AC和直線AB與圓左邊相切和右邊相切.

T：解題時(shí)同學(xué)們應(yīng)注意圓心O在移動(dòng)時(shí)候圖形中位置的變化關(guān)系，考慮周全.

教學(xué)點(diǎn)評：在拿到此題時(shí)“兩種圖形保持相切的關(guān)系有哪幾種”，首先要考慮到圖形相切的定義，在圓與圓的關(guān)系中，相切定義既有內(nèi)切關(guān)系也有外切關(guān)系，因此，審題時(shí)首先考慮到“內(nèi)切”還是“外切”，在不能確定的情況下就要分為兩種情況來討論了；而本題中是考查直線與圓的位置關(guān)系，那么只有一種切線關(guān)系了，但是本題不同的是，本題中有“三條線段”，因此解答時(shí)應(yīng)注意圖形移動(dòng)時(shí)到底是與線段AC，AB，還是BC相切.

4. 復(fù)雜圖形證明問題

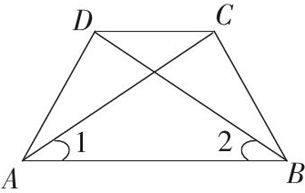
例4 如圖3 ，已知在四邊形ABCD中，AC = BD，∠1 = ∠2，求證： ∠CDA = ∠DCB.

T：根據(jù)已知條件我們可以知道AC = BD，∠1 = ∠2. S：是的.

T：我們可以從圖3中看出線段AB是△ABD和△ABC的公共邊，那么我們可以根據(jù)學(xué)過的三角形證明定理中的哪一個(gè)，得出這兩個(gè)三角形的什么關(guān)系？S：根據(jù)三角形邊角邊（SAS）定理，我們知道△ABD和△ABC這兩個(gè)三角形全等.

T：因?yàn)檫@兩個(gè)三角形全等，所以對應(yīng)角∠ADB和∠ACB也相等（分析： 根據(jù)基本圖形的總結(jié)歸納，學(xué)生很容易發(fā)現(xiàn)例4圖形中包含著軸對稱型的全等三角形，所以學(xué)生能夠證明哪幾個(gè)三角形會(huì)是全等，明確目標(biāo)后就能準(zhǔn)確進(jìn)行答題，從而提高答題的效率）.

教學(xué)點(diǎn)評：很多同學(xué)在初拿到此題時(shí)會(huì)覺得無從下手，因?yàn)轭}設(shè)中給的AC，BD和∠1，∠2與要證明的∠CDA，∠DCB貌似沒有任何關(guān)系. 但是仔細(xì)看圖形就會(huì)發(fā)現(xiàn)，∠CDA = ∠CDB + ∠BDA，∠DCB = ∠DCA + ∠ACB，因此，只要證明∠CDB = ∠DCA，∠BDA = ∠ACB即可，在圖形中，△ABD和△ABC有一個(gè)公共邊AB，因此可以通過這個(gè)公共邊來求出△ABD ≌ △ABC，同樣方法求出△DCB ≌ △DCA，因此可以證明∠CDB = ∠DCA，∠BDA = ∠ACB. 此題給我們的經(jīng)驗(yàn)是，在幾何圖形中當(dāng)要求解的問題與題設(shè)沒有明顯的位置關(guān)系時(shí)，可以把要求解的問題拆分成一些基本的幾何圖形，根據(jù)基本圖形中相對簡單的圖形關(guān)系來探索解題思路，化繁為簡，從而完成求解.

四、總 結(jié)

圖形分類討論是一種十分靈活而又重要的解題法，它最關(guān)鍵的思路就是明確討論的原因及相關(guān)的方法，就是要明白為什么去討論，怎么去討論. 只有思路清晰，那么心中就會(huì)有解題框架，答題就會(huì)條理分明，過程就能嚴(yán)密完整. 通過研究教學(xué)過程和效果，學(xué)生普遍能學(xué)習(xí)領(lǐng)會(huì)如何根據(jù)幾何圖形進(jìn)行變化分類，但是在遇到一些復(fù)雜情況時(shí)，很多學(xué)生的分析還是不容樂觀的，經(jīng)常產(chǎn)生遺漏和重復(fù)討論的現(xiàn)象. 另外，在實(shí)際教學(xué)中作者還發(fā)現(xiàn)很多學(xué)生在畫圖能力、空間想象能力、圖形變化的操控能力等方面比較薄弱，這也是當(dāng)今教育者在教學(xué)上需要改進(jìn)的地方.