非圓柱式對輥破碎機機架動力學分析

楊文杰， 鄧小雷， 徐輝， 陳制衡， 張鵬

（衢州學院機械工程學院，浙江衢州324000）

0 引言

非圓柱式移動對輥破碎機的機架是所有非圓柱式移動對輥破碎機基礎件中最主要的支承部件，是對輥原件及發動機等總成的安裝基礎，在工作中承受很大的沖擊載荷。機架的振動特性對整個機體工作狀態影響很大，而模態是機械結構所固有的振動特性，每一個模態具有自己特定的固有頻率、阻尼比和模態振型，可由計算或試驗分析取得。振動模態是彈性結構固有的、整體的特性。如果通過模態分析方法確定了結構物在某一易受影響的頻率范圍內，各階主要的模態特性，就可能預知結構在此頻段內，在外部或內部各種振源作用下實際振動響應，而且一旦通過模態分析知道模態參數并給予驗證，就可以把這些參數用于（重）設計過程，優化系統動態特性，或者研究把該結構連接到其他結構上時所產生的影響［1］。因此，對機架進行動力學模態分析以獲得其固有頻率和振型是非常有必要的。

1 模態分析的基本理論［2－4］

研究系統的固有振動特性，首先就是要建立該系統的動力方程，而多自由度的運動方程可以應用牛頓第二定律、達朗伯原理、拉格朗日方程和哈密頓定理來建立。對于一個N自由度的線性系統，其運動微分方程為：

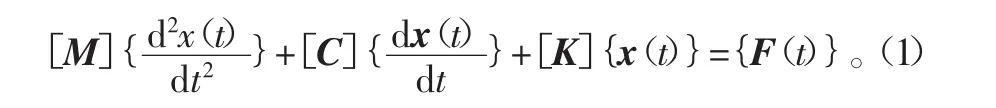
式中，［M］、［C］、［K］分別為系統的質量、阻尼、剛度矩陣，｛x｝及｛F｝分別為系統各點的位移響應向量和激勵力向量。

由于彈性體的自由振動總可以分解為一系列簡諧振動的疊加，為了決定彈性體的自由振動固有頻率及振型，需考慮簡諧振動的解如下∶

式中：｛g｝為位移 x（t）的振幅列向量，與時間 t無關；ω 為固有頻率。將式（2）代入式（1）得∶

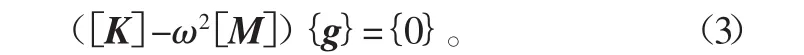
于是求式（1）的簡諧振動就化為令ω和非零向量｛g｝滿足式（2）。ω2就是特征值，振型｛g｝就是特征向量。由 λ=ω2可以決定彈性體的n個固有頻率值：

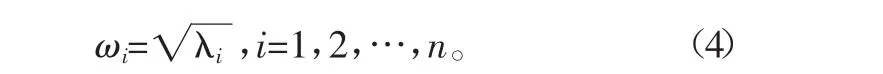
由式（4）可知，特征值只取決于系統本身物理參數。

2 機架模態分析

研究表明，因為高階振型對結構的動力特性的影響較小，所以一般只需要計算出機架較低的幾階頻率。在進行模態分析時，約束設置為地腳螺栓安裝孔內孔面的全約束。通過模態分析，得出前4階的固有頻率和振型。

其分析步驟如下：

1）實體模型導入。將SolidWorks軟件中完成的機架實體模型導入Simulation中。在導入前需對模型進行簡化處理，比如忽略一些倒角、圓角、螺栓孔以及定位孔等對機架影響不大的次要特征，這樣利于后面建立合理的有限元模型。

2）模型網格劃分。選用線性實體單元SOLID92并采用智能分網方式對機架分網格。單元的材料為普通碳鋼，其參數為：屈服強度 E=220 MPa；密度 ρ=7 800 kg/m3；泊松比μ=0.28。單元總數為15451。

3）約束載荷處理。約束設置為機架4根腳的底部的全約束。零部件接觸類型為全局接觸，并設置求解底座前4階的固有頻率和振型。

4）計算及后處理。SolidWorks Simulation計算完成后進入后處理POST1觀看變形形式以便獲得變形量，最終確定最大變形位置。

3 機架模態分析結果

機架的動力學仿真分析后前四階的模態分析結果如圖1～圖4所示。

圖1 第一階振型f=41.677 Hz

圖2 第二階振型f=42.487 Hz

圖3 第三階振型f=61.652 Hz

圖4 第四階振型f=64.353 Hz

機架的一階振型是其一端的縱向擺動，機架二階振型是其一端的整體橫向搖晃，機架三階振型是在X-Z平面的水平扭曲振動，機架四階振型是其在X-Z平面內的單向扭曲振動。而從上述4階振型來看，它們對非圓柱式移動對輥破碎機的零部件的支承的影響各不相同的。整機橫向搖晃引起面板和滑臺相對于機架的位移相對較小。整機的縱向振動雖然有可能會引起破碎機上零部件的相對振動，但振動在縱向上，對破碎石料的精度影響很小。而彎曲振動和扭曲振動都會引起有危害的相對振動，從而使機架上的大型零部件產生相對振動，對加工石料的粒度產生影響。

當然該機架具有較高的低階固有振動頻率，說明該機架比傳統機架結構具有更好的結構動態性能，能很好地滿足破碎機的工作要求。

4 結論

本文通過有限元模態分析分析求解得出其前4階的振型和固有頻率，分別為 f=41.677 Hz、42.487 Hz、61.652 Hz、64.353 Hz，由此，在破碎機機架的優化設計的時候避免與相關的振動源產生共振，為破碎機機架的設計提供了參考，也不失為檢驗機架合理性的一種方法。

［參考文獻］

［1］梁君，趙登峰.模態分析方法綜述［J］.現代制造工程，2006（8）：139-141.

［2］江親瑜，史哲，李寶良.基于ANSYS的高壓低噪小流量離心泵泵體的模態分析［J］.大連交通大學學報，2010（5）：25-28.

［3］許本文，焦群英.機械振動與模態分析基礎［M］.北京：機械工業出版社，1998.

［4］劉國慶.ANSYS工程應用教程機械篇［M］.北京：中國鐵道出版社，2003.