有限元法在工程設計中的應用

張銀玲

（黑龍江省機械科學研究院，哈爾濱150040）

0 引言

在工程技術領域，采用解析方法只能對方程性質簡單且幾何邊界規則的問題進行精確求解，因而，有限元法迅速得到廣泛的應用。有限元法作為近代一種有效的數值計算方法，這種方法將連續的求解域當作是由大量通常被稱為有限元單位的各個子域組成的聯合體，通過對每一個有限元單位假定合適的近似解來推導求解得到問題的解。

1 有限元分析原理

對于彈性體一般三維問題來說，其彈性力學基本方程：

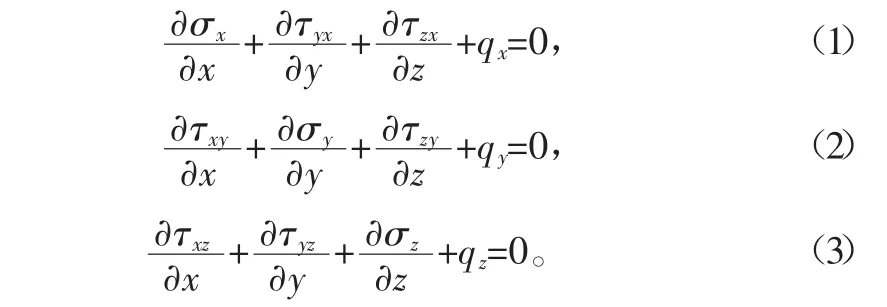
式中，qx、qy和q分別為體積力沿直角坐標系三個方向分量，σx、σy和 σz為正應力，τxy、τyz和 τzx為剪應力。

2 有限元分析流程

1）一般來說，在工程應用中將連續體進行離散化是有限元分析的第一個步驟，同時，這第一步也是進行有限元分析的重要基礎。實際上，離散化過程就是將連續體分割成有限個獨立單元體的過程，但將獨立單元體內的指定點設定為節點，彼此相鄰獨立單元體通過節點相互連接起來組成單元的組合體，從而代替之前的連續體，這個過程就是連續體網格劃分的過程。在網格劃分的過程中，單元形狀的選擇和單元的數目確定是影響網格劃分質量的重要影響因素。在網格劃分的過程中，一般選用三節點三角形單元、四節點矩形單元、六節點三角形單元及其他自選任意形狀單元等。這些選定單元可以具有不同的幾何形狀特征，并且不同形狀特征幾何單元之間也可以采用不同的組合方式，因而網格劃分可以將幾何形狀十分復雜的求解域模型化。

2）經由連續體結構離散化的過程，接下來就要對離散后各個單元進行特性分析。與此同時，在分析連續體時，必須對單元中的位移分布做出部分假設，這樣可以將無限自由度的問題轉化為有限自由度的問題，從而可以采用節點位移來表示單元體內任意一點的位移、應變和應力。依據選定位移模式的特征，可以推導得到有限單元內任意節點的位移關系式，其矩陣形式為：

式中，｛f｝＝［u v w］T為有限單元內任意一點的位移列陣，｛de｝為有限單元節點位移排列形式，［N］為以形函數表示的矩陣，是任意節點位置坐標的函數。

3）建立整個結構的平衡方程。形成總剛度矩陣的通用方法是將全部節點的自由度都按照對號入座原則將每個單元的剛度元素分別疊加到總剛度矩陣的相應位置上，這樣形成的總剛度包括固定約束節點的自由度之內。

在采用有限元方法進行工程設計分析實際應用中，80%的工作量都集中在有限元分析的數據準備和有限元分析的計算結果整理。到目前為止，幾乎所有的有限元分析軟件都能夠提供前處理程序和后處理程序，并且可以自動生成有限元分析所需要的數據模型，尤其是幾何數據模型，同時將自行處理有限元分析結果數據，并將分析結果以圖形的形式表現出來。因此，準確來說，正確理解和使用有限元分析軟件是進行有限元設計分析的重要步驟，其典型的流程如圖1所示。

如圖2所示為某機床工作狀態的有限元分析。

圖1 有限元分析流程

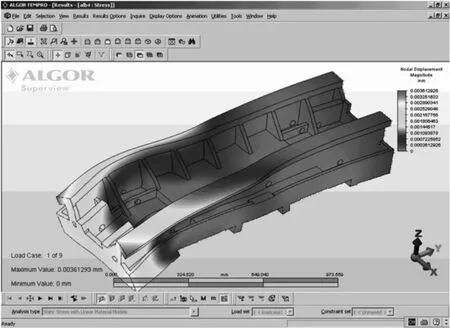
圖2 某機床工作狀態的有限元分析

3 有限元分析發展趨勢

在工程設計中，有限元分析方法的應用范圍從最初的求解彈塑性力學平面幾何解析問題擴展到空間三維或空間多維問題及板殼問題；從求解簡單的力學平衡問題擴展到求解復雜的動力問題、協調問題和穩定性問題；有限元分析的對象也從單一的固體力學擴展到非線性流體力學、電磁領域、微納米領域及熱傳導領域等多學科，目前有限元方法解決的主要問題包括：1）大型復雜結構的穩定性分析；2）金屬、橡膠等材料的大應變分析；3）工程關鍵零部件的線性和非線性分析；4）二維和三維非線性電磁場分析；5）氣動力學分析；6）金屬沖壓成型數值模擬；7）各種邊界條件下的場分析；8）工程構件的彈塑性、蠕變分析。