EGM2008重力場模型的高程異常精度分析

王作鈺

（1. 中鐵第四勘察設計院集團有限公司，湖北 武漢 430063）

EGM2008重力場模型的高程異常精度分析

王作鈺1

（1. 中鐵第四勘察設計院集團有限公司，湖北 武漢 430063）

利用兩條設計鐵路的GPS水準點數據，對EGM2008模型解算的高程異常進行精度統計分析。結果表明，EGM2008模型解算的高程異常在地形平緩的地區精度優于地形起伏較大的山區，且在兩個實驗區中誤差都優于±10 cm。結合一定數量的GPS水準數據，可用于1：2 000航測地形圖外控點的高程擬合。

EGM2008；高程異常；精度分析

EGM2008是精度和分辨率都比較高的地球重力場模型[1-4]，但ICGEM并沒有將其用于驗算中國區域的相關數據。本文以國內區域為實驗對象，利用EGM2008重力場模型直接求解高程異常，進行高程轉換，通過與施測的GPS水準點數據進行對比，來對EGM2008解算的高程異常精度進行評定，以期獲得一些有價值的結論。

1 原理與方法

根據Bruns公式，利用地球重力場模型計算地球表面上任意點的高程異常公式為[5,6]：

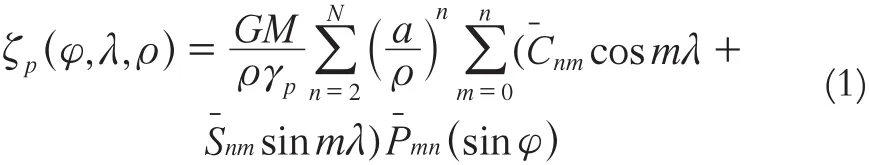
目前通過GPS方法可高精度確定地面點的大地高。若采用水準測量同時確定了該點的正常高，則可以精確地確定該點的高程異常。同時，根據該點坐標及EGM2008重力場模型由公式（1）可計算該點的模型高程異常，通過比較實測高程異常和模型高程異常值，就可以分析模型高程異常的精度，進而確定直接用重力場模型進行高程轉換的精度及可行性。

假設第i點的大地高為Hi，由重力場模型求得該點模型高程異常ζi后，可得該點正常高hi：

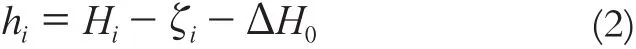
其中， ΔH0為系統性的偏差，主要原因是中國大地水準面和世界大地水準面存在偏差。ΔH0可由下式進行估計：

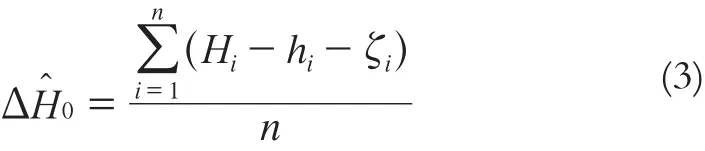
其中，n為公共點點數。結合式（2）和式（3），可利用GPS水準數據對地球重力場模型的精度進行統計分析：

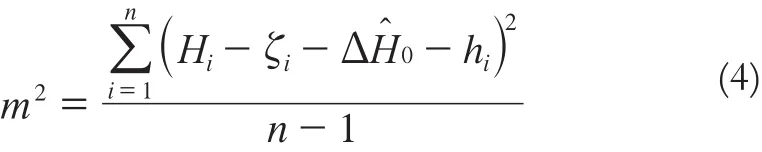
2 計算與分析

本文選擇了一條在建鐵路（貴陽至廣州鐵路）和一條已建成鐵路（石家莊至武漢鐵路）施測的GPS水準數據，對EGM2008地球重力場模型的高程異常解算精度進行統計分析。兩段測區同時施測了GPS數據和三等水準數據。首先利用EGM2008模型計算出每個GPS水準點的模型高程異常，計算時EGM2008模型的階次均取至2 160，不足的球諧位系數以零填補。然后，根據計算出的高程異常結果求出各點正常高并與實測的正常高進行比對，利用式（3）求得系統性偏差，根據（2）式可算出消除系統偏差的正常高，然后利用式（4）進行精度統計。

2.1 貴陽至廣州鐵路GPS水準數據

該線路段控制網成線狀分布，選擇了其中一段控制范圍約150 km，共布設了31個GPS水準點，最短邊長約2 km，最長邊長近7．5 km，平均邊長約5 km，測區為山區地形起伏較大，平均高程約260 m。根據式（1）用EGM2008模型計算出高程異常后直接得到的正常高，與GPS水準數據測得的正常高比較統計結果見圖1。根據圖1可發現，高差在0值上下分布不均勻，存在一定的系統偏差，可根據（3）式計算出系統偏差為-0．079 m。由（2）式所得正常高與GPS水準數據測得的正常高比較統計結果見圖2。從圖2可以看到，經過系統偏差的改正，高差在0值上下分布均勻，且由EGM2008模型所獲得的GPS點的高程異常擬合的正常高精度都在±20 cm之內，最大差值為18．5 cm，最小差值為-17．1 cm，根據（4）式可算得中誤差為±9．8 cm。

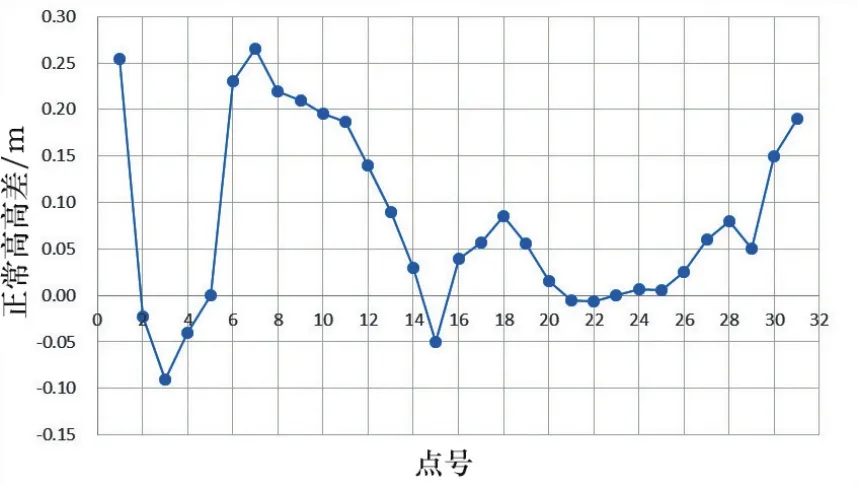
圖1 貴陽至廣州鐵路擬合正常高偏差

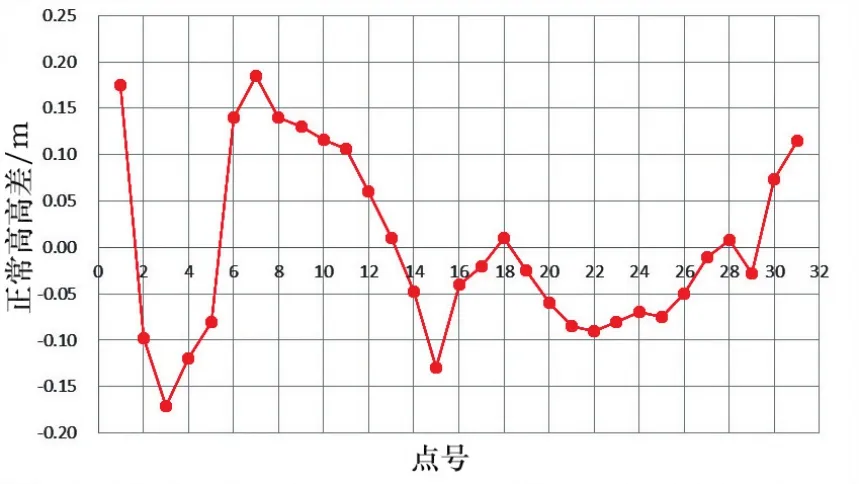
圖2 貴陽至廣州鐵路高程系統經系統偏差改正后擬合正常高偏差

2.2 石家莊至武漢鐵路中段GPS水準數據

該線路段控制網成線狀分布，選擇了其中一段控制范圍約60 km，共布設了31個GPS水準點，最短邊長約1 km，最長邊長近2．2 km，平均邊長約2 km，測區為平原地形較平緩，平均高程約50 m。根據式（1）用EGM2008模型計算出高程異常后直接得到的正常高與GPS水準數據測得的正常高比較統計結果見圖3。根據圖3可發現，高差在0值上下分布不均勻，存在一定的系統偏差。可根據（3）式計算出系統偏差為-0．068 m。由（2）式所得正常高與GPS水準數據測得的正常高比較統計結果見圖4。從圖4可以看到，經過系統偏差改正，高差在0值上下分布均勻，且由EGM2008模型所獲得的GPS點的高程異常擬合的正常高精度都在±15 cm之內，最大差值為11．1 cm，最小差值為-15．5 cm，根據（4）式可算得中誤差為±5．9 cm。

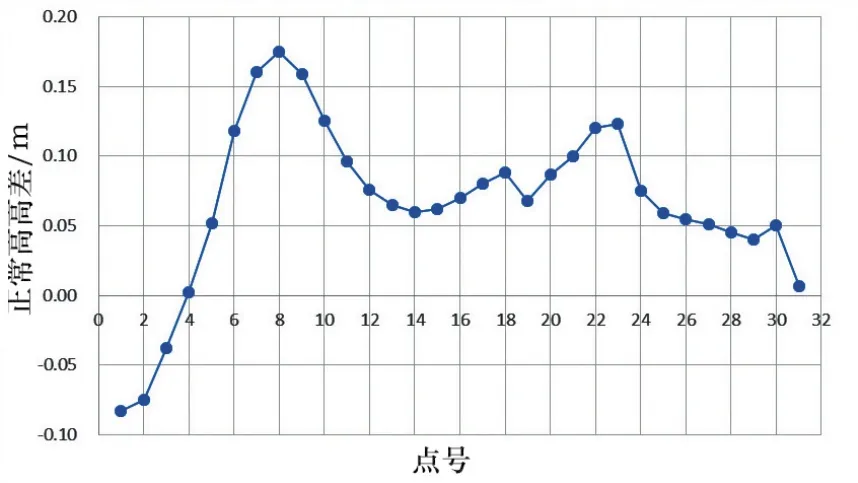
圖3 石家莊至武漢鐵路擬合正常高偏差

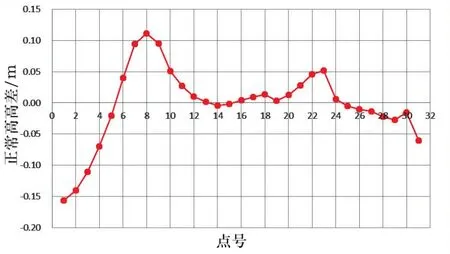
圖4 石家莊至武漢鐵路高程系統經系統偏差改正后擬合正常高偏差

3 結 語

本文采用EGM2008重力場模型解算高程異常進行高程轉換，利用兩個不同地形條件的GPS 水準數據對EGM2008重力場模型轉換的正常高精度進行對比分析，得出如下結論：①EGM2008模型在地形平緩的平原地區求解的高程異常精度優于地形起伏大的山區。②貴陽至廣州鐵路和石家莊至武漢鐵路兩測區的高程系統和EGM2008模型所采用的高程系統存在一定的系統偏差。③EGM2008模型的高程異常精度較高，中誤差可達到±10 cm，結合一定量的GPS水準點進行高程擬合，可用于1︰2 000地形圖航測外控點的高程轉換。

[1] 魏子卿．GPS重力位水準[J]．大地測量與地球動力學，2007(4)：1-7

[2] 夏哲仁，石磐，李迎春．高分辨率區域重力場模型DQM 2000[J]．武漢大學學報：信息科學版，2003，28(特刊)：124-128

[3] Pavlsn N K，Holmes S A，Kenyon S C，et al．An Earth Gravitational Model to Degree 2160:EGM 2008[R]．General Assembly of the European Geosciences Union，2008(4)：13-14

[4] 張興福，劉成，劉紅新．利用GPS /水準數據檢核EGM2008重力場模型的精度[J]．測繪通報，2009(2): 7-9

[5] Heiskanen W，Moritz H． Physical Geodesy[M]． San Francisco:Freeman W H，1967

[6] 孔祥元，郭際明，劉宗泉． 大地測量學基礎[M]．武漢:武漢大學出版社，2005

[7] 侯俊嶺． 高精度地球重力場模型用于GPS高程轉換[J] ．鐵道勘察，2010(6)：15-17

P223.0

B

1672-4623（2014）03-0110-02

10.11709/j.issn.1672-4623.2014.03.036

王作鈺，工程師，研究方向為測繪工程。

2013-12-26。