模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)數(shù)據(jù)處理探討

田建波, 程 喆,陳 于

（1.中國人民解放軍61365部隊(duì),天津 300140；2.中國地質(zhì)大學(xué)（武漢）信息工程學(xué)院，湖北 武漢430074；3.中國人民解放軍61175部隊(duì)，湖北 武漢430074）

模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)數(shù)據(jù)處理探討

田建波1, 程 喆2,3,陳 于2

（1.中國人民解放軍61365部隊(duì),天津 300140；2.中國地質(zhì)大學(xué)（武漢）信息工程學(xué)院，湖北 武漢430074；3.中國人民解放軍61175部隊(duì)，湖北 武漢430074）

為了提高監(jiān)測數(shù)據(jù)分析與預(yù)報(bào)的準(zhǔn)確性、實(shí)時(shí)性，提出將模擬退火算法與粒子群BP神經(jīng)網(wǎng)絡(luò)相結(jié)合應(yīng)用于變形監(jiān)測數(shù)據(jù)處理中。分別分析了3種方法的原理和計(jì)算過程，闡述了新方法的計(jì)算步驟，并通過實(shí)例說明該方法比傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)法擬合和預(yù)報(bào)效果更好。

模擬退火法；粒子群算法；BP神經(jīng)網(wǎng)絡(luò)；監(jiān)測數(shù)據(jù)

BP神經(jīng)網(wǎng)絡(luò)是一種采用誤差反向傳播訓(xùn)練算法的多層前饋神經(jīng)網(wǎng)絡(luò)，在處理非線性、無規(guī)則的問題時(shí)具有很強(qiáng)的優(yōu)越性，廣泛應(yīng)用于大壩變形預(yù)測與安全監(jiān)控[1,2]、工程變形監(jiān)測[3]、滑坡位移預(yù)測[4,5]和GPS水準(zhǔn)高程轉(zhuǎn)換[6]等領(lǐng)域；但其存在收斂速度慢、輸出結(jié)果容易受初始值影響等缺點(diǎn)。針對(duì)這些缺點(diǎn)，提出了遺傳模擬退火算法的BP算法[7]、BP網(wǎng)絡(luò)優(yōu)化的并行模擬退火遺傳算法[8]、基于遺傳算法的模糊神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)和參數(shù)優(yōu)化[9]、基于L-M算法的BP神經(jīng)網(wǎng)絡(luò)分類器[10]、改進(jìn)激活函數(shù)的人工神經(jīng)網(wǎng)絡(luò)[11]等改進(jìn)方法。粒子群優(yōu)化算法是一種基于群體智能方法的計(jì)算技術(shù)，收斂速度快，但精度一般較低；而基于粒子群優(yōu)化算法的多因子自適應(yīng)濾波[12]和改進(jìn)粒子群耦合[13]方法能較好地克服此缺點(diǎn)。模擬退火法是基于模擬固體物質(zhì)退火過程的優(yōu)化算法[14,15]，輸出結(jié)果質(zhì)量高但過程時(shí)間長。鑒于3種方法的優(yōu)缺點(diǎn)，本文提出將粒子群優(yōu)化算法與模擬退火法相結(jié)合應(yīng)用于BP神經(jīng)網(wǎng)絡(luò)中，進(jìn)行GPS監(jiān)測數(shù)據(jù)處理分析，通過與傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)對(duì)比研究，證明該方法的可行性與實(shí)用性。

1 模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)預(yù)測模型

模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)模型在進(jìn)行變形監(jiān)測分析時(shí)，是以模擬退火法BP神經(jīng)網(wǎng)絡(luò)為基礎(chǔ)，運(yùn)用粒子群優(yōu)化算法進(jìn)行初始權(quán)值的計(jì)算。

1.1 BP神經(jīng)網(wǎng)絡(luò)

BP神經(jīng)網(wǎng)絡(luò)是基于誤差逆向傳播訓(xùn)練算法的多層前饋神經(jīng)網(wǎng)絡(luò)，由輸入層、隱含層和輸出層組成。信號(hào)正向傳播的輸出值與預(yù)定值相比得出誤差，誤差反向傳播訓(xùn)練糾正神經(jīng)元的權(quán)值和閾值，如此迭代，使誤差逐步減小，直至誤差小于給定值時(shí)，學(xué)習(xí)結(jié)束，如圖1所示。其中，W為各個(gè)輸入神經(jīng)元與隱含層神經(jīng)元以及隱含層神經(jīng)元與輸出層神經(jīng)元的連接權(quán)；V為各個(gè)隱含層以及輸出層神經(jīng)元的閾值。

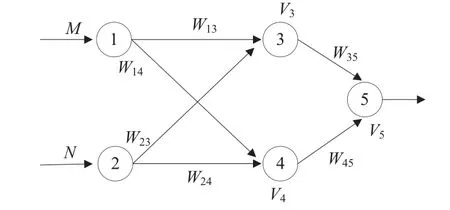
圖1 BP神經(jīng)網(wǎng)絡(luò)圖

1.2 粒子群優(yōu)化算法

粒子群優(yōu)化算法(PSO)是一種基于群體智能方法的演化計(jì)算技術(shù)，每個(gè)優(yōu)化問題的可能解都是搜索空間的一個(gè)粒子，每個(gè)粒子有優(yōu)化函數(shù)決定的適應(yīng)值，還有決定粒子方向和距離的速度。PSO初始化為一群隨機(jī)粒子進(jìn)行迭代尋優(yōu)。每次尋優(yōu)的單個(gè)粒子都通過跟蹤當(dāng)前種群中的最優(yōu)解和當(dāng)前“鄰居”中的最優(yōu)解來更新自己，最終找到最優(yōu)解。

粒子群優(yōu)化算法的具體流程為[1]：

1）初始化：在允許的范圍內(nèi)隨機(jī)產(chǎn)生初始粒子的位置x0和速度v0，每個(gè)粒子的局部最優(yōu)解pbest坐標(biāo)設(shè)置為其當(dāng)前位置，計(jì)算出所有個(gè)體極值點(diǎn)的適應(yīng)度值，選取所有個(gè)體極值點(diǎn)適應(yīng)度值中最好的作為全局最優(yōu)解gbest，gbest坐標(biāo)設(shè)置為最好粒子的當(dāng)前位置。

2）粒子評(píng)價(jià)：重新計(jì)算粒子的適應(yīng)度值，如果優(yōu)于當(dāng)前粒子個(gè)體極值點(diǎn)適應(yīng)度值，則將pbest設(shè)置為該粒子的位置，并更新個(gè)體極值點(diǎn)適應(yīng)度值。如果所有粒子的個(gè)體極值點(diǎn)適應(yīng)度值中最好的優(yōu)于全局極值，則更新全局極值并將gbest設(shè)置為該粒子的位置。

3）更新粒子：

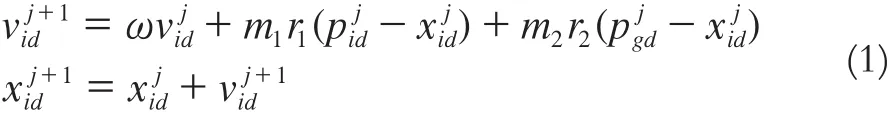
式中，i=1,2,3，…，m，為粒子的總個(gè)數(shù)；d=1,2,3，…，D，為搜索空間的維數(shù)；ω為慣性權(quán)重；m1、m2為權(quán)重因子；r1、r2為0到1之間的隨機(jī)數(shù)為第 j次迭代的粒子i位置矢量的第d維分量為第j次迭代的粒子i飛行速度矢量的第d維分量為第j次迭代的粒子i最好個(gè)體位置pbest的第d維分量為第j次迭代的粒子群最好位置gbest的第d維分量。

4）檢驗(yàn)結(jié)果：若達(dá)到迭代結(jié)束的條件(迭代次數(shù)達(dá)到或迭代誤差小于給定值)則結(jié)束迭代，輸出最優(yōu)解，否則轉(zhuǎn)到步驟2）。

1.3 模擬退火法

模擬退火法（SA）是基于組合優(yōu)化問題與固體物質(zhì)退火過程的相似性,在模擬固體物質(zhì)退火的過程中尋求最優(yōu)解[2]。算法具體步驟如下：

1）指定退火法初始溫度T0和當(dāng)前狀態(tài)i。

2）通過擾動(dòng)產(chǎn)生新狀態(tài)j，計(jì)算目標(biāo)函數(shù)Fi和Fj，如果Fi＞Fj，接受j為當(dāng)前溫度的新狀態(tài)；否則通過概率判斷是否接受新的狀態(tài)：

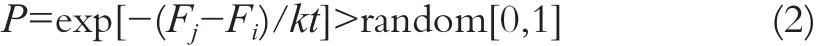
式中，k為boltzmann常數(shù)。

1.4 模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)預(yù)測模型

針對(duì)BP神經(jīng)網(wǎng)絡(luò)的初始連接權(quán)初始化效果不一定理想和收斂較慢的實(shí)際情況，使用粒子群優(yōu)化算法優(yōu)化初始權(quán)，模擬退火法代替誤差反向傳播訓(xùn)練法，提高神經(jīng)網(wǎng)絡(luò)收斂速度和學(xué)習(xí)能力。具體流程如下：

1）BP神經(jīng)網(wǎng)絡(luò)的構(gòu)建。將影響變形監(jiān)測的因素（氣溫、季節(jié)、空氣濕度等）作為輸入層神經(jīng)元，將變形量（水平、垂直位移等）作為輸出層神經(jīng)元。隱含層神經(jīng)元的個(gè)數(shù)一般由式（3）確定：

式中，l為隱含層神經(jīng)元個(gè)數(shù)；p為輸入層神經(jīng)元個(gè)數(shù)；q為輸出層神經(jīng)元個(gè)數(shù)。

2）給定粒子總數(shù)m、慣性權(quán)重ω、權(quán)重因子m1和m2、搜索空間維數(shù)D（網(wǎng)絡(luò)中所有連接權(quán)的個(gè)數(shù)）、

3）選定輸出層誤差平方和為適應(yīng)度函數(shù)，即

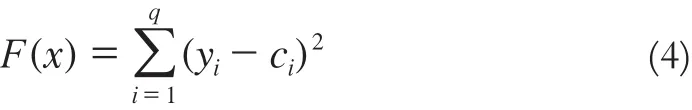
式中，q為輸出層神經(jīng)元個(gè)數(shù)(一般為變形量)；y和c分別為實(shí)測值和輸出值。

4）隨機(jī)初始化連接權(quán)為一群粒子，具體編碼格式如下：

粒子位置：X1，X2，X3，…，XD

粒子速度：V1，V2，V3，…，VD

適應(yīng)度函數(shù)：F（x）

5）計(jì)算各個(gè)粒子的適應(yīng)度。

6）將每個(gè)粒子的適應(yīng)度和局部最好適應(yīng)度pbest比較，若超過局部最好適應(yīng)度pbest，則將該粒子的位置作為局部最好pbest；再將該粒子的適應(yīng)度與全部最好適應(yīng)度gbest比較，若超過全局最好適應(yīng)度gbest，將該粒子作為全局最好gbest。

7）利用式（1）更新粒子的具體位置X和速度V。

8）在解空間進(jìn)行搜索，如果超過規(guī)定的迭代次數(shù)或達(dá)到預(yù)定的精度要求，停止迭代，將最優(yōu)解gbest作為BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值；否則轉(zhuǎn)入步驟5）。

9）將輸入和輸出的數(shù)據(jù)統(tǒng)一進(jìn)行格式化處理：

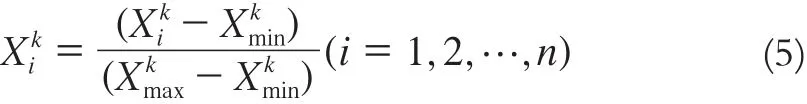
10）利用Rand函數(shù)進(jìn)行輸出層和隱含層的閾值V的初始化，所有連接權(quán)值已經(jīng)初始化完畢。初始溫度T0可以隨意給定。

11）BP神經(jīng)網(wǎng)絡(luò)根據(jù)已有的輸入樣本、連接權(quán)和閾值得出輸出結(jié)果，與理想結(jié)果相比得出誤差；再進(jìn)行一次誤差反向傳播訓(xùn)練法得出新的連接權(quán)和閾值。

12）將新的閾值V和連接權(quán)W作為模擬退火法在該溫度T0下的初態(tài)j[3,4]，新狀態(tài)按照柯西分布：

式中，x為0到1之間的隨機(jī)數(shù)；t為當(dāng)前溫度。

13）確定能量函數(shù)(目標(biāo)函數(shù))：

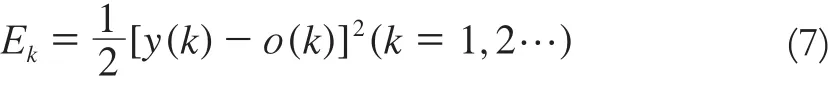
式中，y（k）為實(shí)際值；o（k）為網(wǎng)絡(luò)完成輸出后，執(zhí)行Metropolis準(zhǔn)則并滿足內(nèi)循環(huán)的停止準(zhǔn)則，輸出的權(quán)值和閾值[5-7]。

14）將輸出權(quán)值和閾值作為網(wǎng)絡(luò)的新值計(jì)算目標(biāo)函數(shù)，如果目標(biāo)函數(shù)與實(shí)際值的差滿足精度要求，停止外循環(huán)并輸出變形觀測數(shù)據(jù)的預(yù)測值；否則降溫處理轉(zhuǎn)到步驟12）。

具體流程如圖2所示。

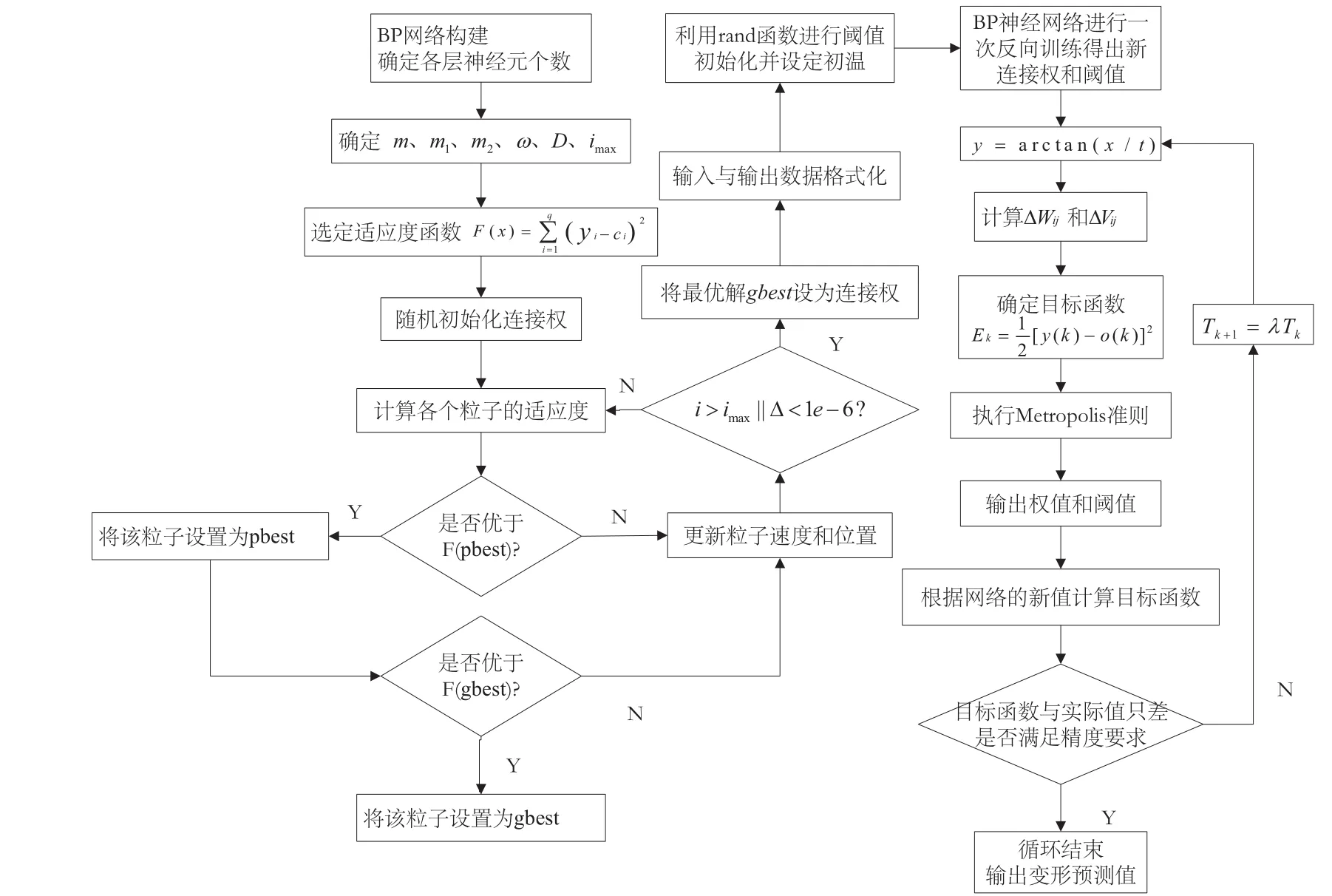
圖2 算法流程圖

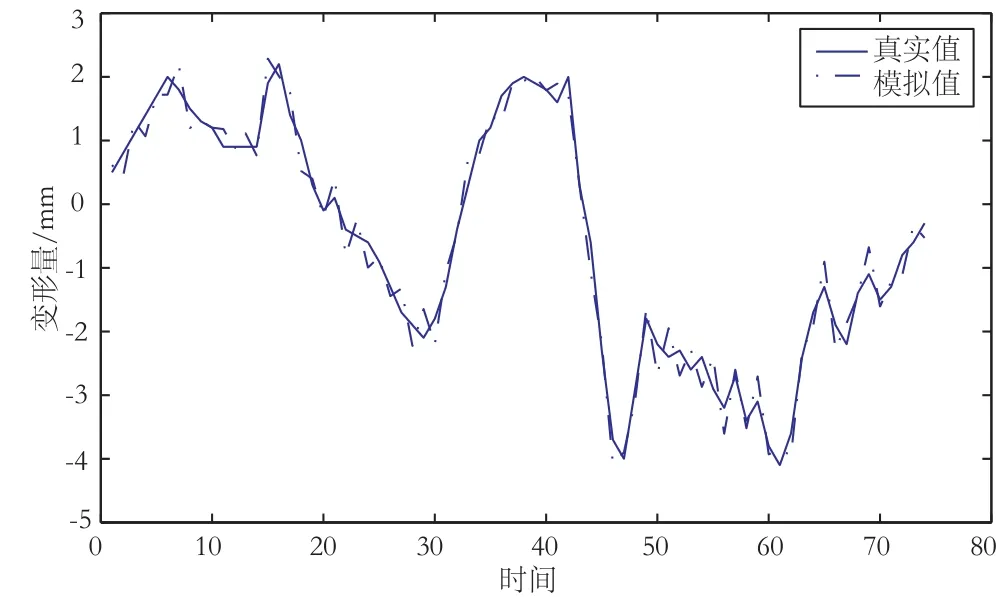
圖3 BP神經(jīng)網(wǎng)絡(luò)模擬效果圖

2 算例與分析

選取某大壩2009-05-17～2009-10-19監(jiān)測數(shù)據(jù)，分析沿河流方向的位移變形量。將2009-05-17作為基準(zhǔn)日，對(duì)監(jiān)測數(shù)據(jù)坐標(biāo)、水位和氣溫進(jìn)行處理，得到相對(duì)于基準(zhǔn)日的相對(duì)坐標(biāo)、水位和氣溫；確定BP神經(jīng)網(wǎng)絡(luò)輸入層有水位分量、溫度因子、時(shí)效因子3類節(jié)點(diǎn)，輸出層節(jié)點(diǎn)一個(gè)，即X方向位移量；分別采用單純的BP神經(jīng)網(wǎng)絡(luò)法和模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)進(jìn)行模擬，效果如圖3、圖4所示。

新方法的模擬效果要明顯優(yōu)于單純的BP神經(jīng)網(wǎng)絡(luò)方法；再分別利用2種方法對(duì)2009-10-12～2009-10-19的變形量進(jìn)行預(yù)報(bào)（見表1）。

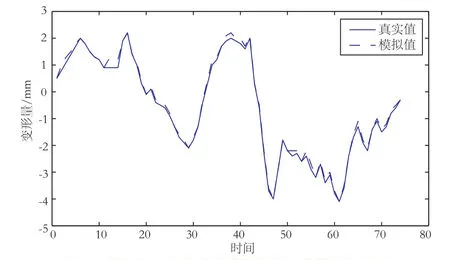
圖4 模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)模擬效果圖

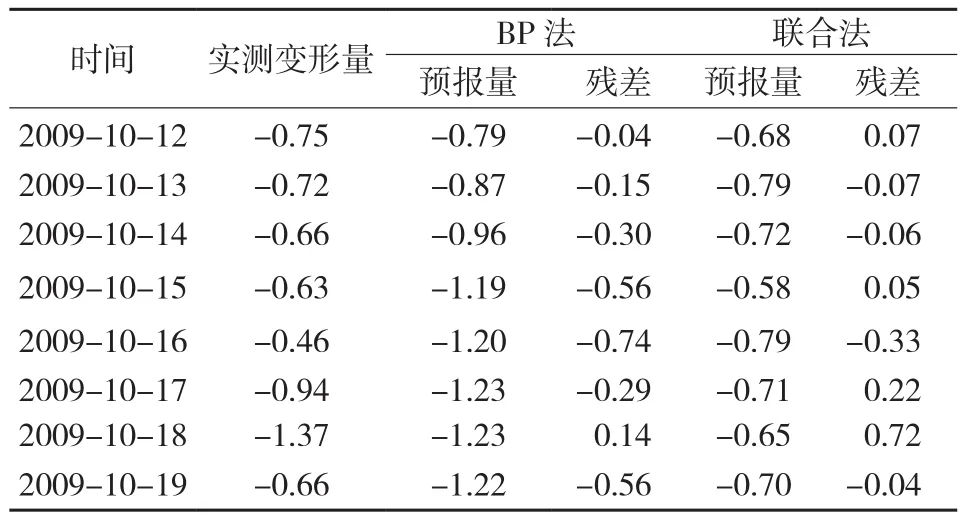
表1 模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)與單純BP神經(jīng)網(wǎng)絡(luò)預(yù)報(bào)值對(duì)比分析表/mm

由表1可知，模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)預(yù)報(bào)值殘差要明顯小于單純BP神經(jīng)網(wǎng)絡(luò)殘差，預(yù)報(bào)值更準(zhǔn)確。

3 結(jié) 語

本文提出模擬退火的粒子群BP神經(jīng)網(wǎng)絡(luò)，將模擬退火法、粒子群法和BP神經(jīng)網(wǎng)絡(luò)結(jié)合起來，經(jīng)過實(shí)例驗(yàn)算證明其預(yù)測效果優(yōu)于單純的BP神經(jīng)網(wǎng)絡(luò)法。該方法對(duì)于提高GPS監(jiān)測數(shù)據(jù)處理分析的速度與靈敏度具有實(shí)際意義。

[1] 李捷斌, 孔令杰． 基于Kalman濾波的BP神經(jīng)網(wǎng)絡(luò)方法在大壩變形預(yù)測中的應(yīng)用[J]． 大地測量與地球動(dòng)力學(xué), 2009, 29(4): 124-128

[2] 蘇懷智, 吳中如, 溫志萍，等． 基于模糊聯(lián)想記憶神經(jīng)網(wǎng)絡(luò)的大壩安全監(jiān)控系統(tǒng)建模研究[J]． 武漢大學(xué)學(xué)報(bào)：工學(xué)版, 2001, 34(4): 21-25

[3] 劉祖強(qiáng), 張正祿． 工程變形監(jiān)測分析預(yù)報(bào)的理論與實(shí)踐[M]．北京：中國水利水電出版社，2008

[4] 彭令, 牛瑞卿, 趙艷南，等． 基于核主成分分析和粒子群優(yōu)化支持向量機(jī)的滑坡位移預(yù)測[J]． 武漢大學(xué)學(xué)報(bào)：信息科學(xué)版, 2013, 38(2): 148-154

[5] 武雪玲, 任福, 牛瑞卿． 多源數(shù)據(jù)支持下的三峽庫區(qū)滑坡災(zāi)害空間智能預(yù)測[J]． 武漢大學(xué)學(xué)報(bào)：信息科學(xué)版, 2013, 38(8): 963-969

[6] 王殊偉, 李斐, 柯寶貴，等． 基于BP神經(jīng)網(wǎng)絡(luò)算法的GPS水準(zhǔn)高程轉(zhuǎn)換[J]． 武漢大學(xué)學(xué)報(bào)：信息科學(xué)版, 2009, 34(10): 1 190-1 195

[7] 張世龍, 唐雅娜． 基于遺傳模擬退火算法的BP算法研究[J]．現(xiàn)代計(jì)算機(jī), 2007(2): 30-33

[8] 劉月娥, 何東健, 李崢嶸． 一種用于BP網(wǎng)絡(luò)優(yōu)化的并行模擬退火遺傳算法[J]．計(jì)算機(jī)應(yīng)用, 2006, 26(1): 204-207

[9] 周志堅(jiān), 毛宗源． 一種基于遺傳算法的模糊神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)和參數(shù)優(yōu)化[J]． 華南理工大學(xué)學(xué)報(bào)：自然科學(xué)版, 1999, 27(1): 26-33

[10] 王建梅, 覃文忠． 基于L-M算法的BP神經(jīng)網(wǎng)絡(luò)分類器[J]．武漢大學(xué)學(xué)報(bào)：信息科學(xué)版, 2005, 30(10): 928-932

[11] 胡耀垓, 李偉, 胡繼明． 一種改進(jìn)激活函數(shù)的人工神經(jīng)網(wǎng)絡(luò)及其應(yīng)用[J]． 武漢大學(xué)學(xué)報(bào)：信息科學(xué)版, 2004, 29(10): 916-920

[12] 聶建亮, 程傳錄, 郭春喜，等． 基于粒子群優(yōu)化算法的多因子自適應(yīng)濾波[J]． 武漢大學(xué)學(xué)報(bào)：信息科學(xué)版, 2013, 38(2): 136-140

[13] 王偉, 沈振中． 大壩統(tǒng)計(jì)預(yù)警模型的改進(jìn)粒子群耦合方法[J]．武漢大學(xué)學(xué)報(bào)：信息科學(xué)版, 2009, 34(8): 987-992

[14] 范千, 許承權(quán)．單純形—模擬退火混合算法及其在參數(shù)估計(jì)中的應(yīng)用[J]． 地理空間信息, 2005， 3(3): 57-59

[15] 胡山鷹, 陳丙珍, 何小榮，等．非線性問題全局優(yōu)化的模擬退火法[J]． 清華大學(xué)學(xué)報(bào)：自然科學(xué)版, 1997, 37(6): 5-9

P258

B

1672-4623（2014）03-0069-04

10.11709/j.issn.1672-4623.2014.03.022

田建波，碩士，高級(jí)工程師，研究方向?yàn)镚NSS數(shù)據(jù)處理與應(yīng)用。

2014-01-20。

項(xiàng)目來源：湖北省自然科學(xué)基金資助項(xiàng)目（2011CDB350）。