從課例對比看數學課堂的歷史變遷

婁森鋒

筆者參加了市小學數學學科帶頭人課堂教學評比活動，聽了多節參加評比的老師的《積的變化規律》的課，也參與了其中一堂課的磨課活動。在這個過程中，無意間看到1995年4月刊登在《湖南教育》時任江蘇南京實驗國際學校校長、特級教師盛大啟的一節《積的變化規律》的課例。自然而然地就把2013年的課和1995年的課進行了對比，發現了很多有意義的地方。

在這里要說明的是1995年、2013年的課，都是在當時社會背景下產生的，都是在當時課程理念的指導下的，沒有要比出孰優孰劣的意思。而且盛大啟老師在當時是特級教師，課例還刊登在省級刊物《湖南教育》上，所以盛大啟老師的《積的變化規律》的課例在當時肯定是最好的，最具代表性的。

筆者把2013年的課和1995年的課進行對比，主要是想看看我們的數學課堂到底發生了什么樣的變化，是否是趨于正確的價值取向的變化。

為了表達方便，1995年的課例下面簡稱為A，2013年的三節課例簡稱為B、C、D。

一、引入環節

A課：1.布置學生在課本上把例6的表（如下表）填寫完整，然后指名說出填寫結果。2.引導學生進行觀察、討論。

B課：1.口算2×3= 2×6= 2×18= ；20×6= 10×12=

5×24= 2.獨自練習后反饋校對。觀察比較這兩組算式的異同點。（積變化、積不變）3.今天我們研究第一組算式，積的變化規律。2×3=6，2×6=12，2×18=36

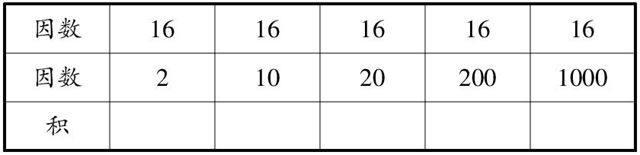
C課：1.計算長方形的面積板書：20×12=240，在乘法算式中，20、12、240分別叫什么？（板書：因數 因數 積）2.計算20×36長方形的面積，還有別的計算方法嗎？你是怎么想的？3.計算20×60長方形的面積。4.觀察算式：你有什么發現？20×12=240，20×36=720，20×60=1200。

D課：1.涂色。方格紙每格長度是8厘米，寬度是2厘米，把其中一小格涂上陰影，計算陰影的面積。2.再涂上一格，面積是多少呢？3.再涂上一格，面積是多少呢？4.如果再畫下去，想象并回答：現在涂陰影的大長方形的面積是多少呢？

差異：選擇了不同的邏輯起點。恰當的教學起點是教學有效性的保證。A課前面有復習環節，看似降低了教學起點，其實不然。因為積的變化規律的發現是通過觀察的方式，在A課中的表格里面讓學生自主觀察得到積的變化規律不難，但讓學生真正理解規律的內涵，用自己的方式來表達，甚至推廣到其他的乘法算式時，難度就增加了不少。

B、C、D課的教學起點的把握上相對低一點，讓學生縱向觀察三個算式，說說你有什么發現。C、D兩課更低，提供了長方形幫助學生直觀體驗，再觀察算式，給學生架起了腳手架。

二、形成規律

A課：引導學生進行觀察、討論：①從左往右，逐條提示進行觀察，得出結論；②從右往左，逐條提示進行觀察，得出結論。

B課：觀察比較，形成猜想。2×3=6，2×6=12，2×18=36 1.觀察第一組算式，一個因數不變，另一個因數發生怎樣的變化，積也發生怎樣的變化？2.形成猜想：一個因數不變，另一個因數乘幾，積也乘幾。

C課：觀察算式：你有什么發現？20×12=240，20×36=720，20×60=1200板書：一個因數不變，另一個因數×（ ），積也跟著×（ ）。

D課：8×2=16，8×4=32，8×6=48，8×8=64，8×10=80……1.改長寬為一個因數和另一個因數，面積為積，現在你能說說剛才這一變化規律嗎？2.生：……3.師：一個因數不變，一個因數×11，積×？一個因數×15，積×？一個因數×100，積×？4.師：一個因數不變，一個因數×a，積×？……

差異：獨立思考，學會表達和傾聽，形成猜想和熟練地進行積的變化規律的運用，哪個更重要的取向不同。這是兩個時代課中最大差異之一。現在，也就是B、C、D課是取前者。

這是時代對人的能力的要求在提高的一種表現。社會要求我們的教學要著眼于學生整體素質的提高，促進學生較好地發展，當然設計的活動要適應學生未來生活、工作、學習的需要。會思考、能表達、有想法、能解決問題這是作為人的基本能力要求。這些都需要在課堂教學中予以落實。因此，在新授課中我們要注重過程，再設置練習課，注重“雙基”落實。

三、驗證規律

A課：觀察表格得出的規律就是正確的規律，轉而進行了練習。

B課：1.學生舉例來驗證規律。2.有沒有不成立的例子？3.你有沒有其他猜想？一個因數不變，另一個因數除以幾，積也除以幾。4.學生再次舉例驗證。5.再次猜想。一個因數不變，另一個因數加上幾或減去幾，積也加上幾或減去幾。6.學生舉例驗證。7.師：如果找到了反例，我們就說規律不成立。

C課：1.這組算式有這樣的規律，那其他的乘法算式也有這樣的規律嗎？不能確定，那怎么辦？2.舉例驗證。（教給學生方法）3.他舉的例子有這樣的規律嗎？你們怎么看出來的？4.你發現了什么？“一個因數不變，另一個因數÷（ ），積也跟著÷（ ）”5.獨立舉例驗證。6.全班交流，得出規律。7.把兩句結論進行合并。

D課：1.舉例驗證。2.學生思考后口頭舉例。反饋，教師板書。3.學生自己舉例。4.應用規律。（1）8×25=200，那么（8×6）×25=200×（ ）……5.遷移：那么一個因數不變，另一個因數除以幾，積也除以幾。會對嗎？6.學生舉例驗證。7.質疑：另一個因數除以幾，可以是0嗎？為什么？（0不可以做除數。）8.應用規律。

差異一：舉例驗證規律。A課中當師生共同完成對表格的觀察，發現“一個因數不變，另一個因數擴大或縮小若干倍，積也擴大或縮小相同的倍數”的規律，就認為這是正確的，教師不再作處理。B、C、D課中規律的呈現是學生猜想出來的，只在一組算式中成立，需要在其他組算式中驗證，方成為正確的規律。具體驗證過程見右圖“B、C、D課規律驗證過程”，所不同的是，B課的驗證過程比較完整，C、D課只進行了乘和除兩種情況的驗證。

我們看到，學習方式的選擇是1995年課和2011年課最大的區別。

差異二：合情推理，也就是歸納類比推理能力的培養。A課中沒有合情推理的環節設置，所有的規律都是在表格中或算式中觀察發現的。在B、C、D課中，當完成第一猜想的驗證后，教師都采用了合情推理來引出“猜想2：一個因數不變，另一個因數除以幾，積也除以幾”，讓學生繼續來驗證。B課更是引導學生推理出“一個因數不變，另一個因數加或減幾，積是否也加或減幾”的猜想，把合情推理做到了極致。

B、C、D課規律驗證過程圖

我們看到課堂教學始終帶著明顯的時代烙印，因此我們要善于抓住本質展開教學，“材料簡單，過程豐富，結果深刻”是現在《積的變化規律》教學的訴求。

（作者單位 浙江省臨安市博世凱實驗小學）

編輯 劉青梅