計及機組不確定損耗成本的魯棒安全經濟調度

劉鴻，劉建華，唐民

（1.長沙理工大學電氣與信息工程學院，長沙 410004；2.慈溪市供電局，慈溪 315300）

電力系統的經濟運行一直以來都是電力工程技術人員和學者研究的問題。電力系統的經濟性是以安全性為前提的。文獻[1～2]介紹了考慮直流潮流和線路容量約束條件的經濟調度ED（economic dispatch）模型，稱該模型為經濟安全調度ESD（economic safe dispatch）模型。傳統的ESD基本目標是在滿足有功功率平衡情況下發電費用最小，機組出力及線路安全約束也應得到滿足。這是一個非線性問題，求解這類問題的方法很多，諸如非線性規劃法[3～4]，二次規劃法[5]，逐次線性法[6]，神經網絡[7～8]等等。以上方法都是基于ESD模型中的參數是確定的。而電力系統在實際運行中各參量并不是嚴格意義上具有確定性的，是具有一定的不確定性（如線路參數、電網的拓撲結構等），傳統的ESD問題把不確定性因素當作確定性因素來處理，得出的最優解并非真正切合實際的最優解。在ESD問題中，發電機的費用函數曲線是通過“熱運行”實驗所得到的數據點繪制而成[9]，通過這些數據點擬合成二次函數，本身存在一定的誤差。火電機組出力是通過由燃煤和各種化石燃料等給鍋爐中的水加熱，產生蒸汽，由蒸汽推動汽輪機轉動，進一步帶動發電機轉子轉動產生電能，是由熱能轉化為機械能，再轉化為電能的過程。這中間的能量轉化并非理想狀態下的轉化，而是存在諸多不確定性。而環境溫度以及海水和湖泊水等作為用來作為冷卻蒸汽的溫度也存在不確定性，所以不能在任何時刻都用確定性的發電成本二次函數來進行描述，而是應該計及這些不確定性因素對機組煤耗產生的附加成本。故本文旨在修正這些不確定性因素所帶來的附加成本對模型本身所帶來的誤差，以期更接近實際最優運行值。

目前，許多優化方法都運用到了ESD問題中，但是大多數的方法都是通過建立ESD潮流模型，如何有效的去求解，已有的這些方法并不能處理模型中的不確定性因素。近年來，各國研究者對已有的研究并不滿足，迫切需要尋找一種方法來處理那些不確定性因素引起的誤差，希望得到更貼切實際的優化值。而魯棒優化方法[10]的提出正是解決這類問題的較好的方法，它能考慮最壞（worstcase）情況下的狀態，本文利用魯棒優化方法對電力系統煤耗參數的不確定性進行描述，模擬仿真表明該方法的有效性和在實踐中具有重要的理論指導意義。

1 “不確定損耗成本”的描述

目前，電力是通過各種能源（如燃燒煤和各種化石燃料，核能裂變，風能等）所轉化的，本文考慮利用煤和各種化石燃料生產電能，它的基本生產過程是：燃料在鍋爐中燃燒加熱水變成蒸汽，經過加熱器進一步加熱后變成過熱的蒸汽，再通過主蒸汽管道進入汽輪機。由于蒸汽不斷膨脹，高速流動的蒸汽推動汽輪機的葉片轉動從而帶動發電機從而產生電能。最后將做過功的蒸汽排入凝汽器并被冷卻凝結成水，經過低壓和高壓加熱后將熱水打入鍋爐，通常都是用海水和湖泊水作為凝汽器冷卻。通過不斷循環產生源源不斷的電能。這個汽水系統總是受環境因素的影響，如空氣、海水溫度等。

為了進一步提高其熱效率，一般都從汽輪機的某些中間級后抽出做過功的部分蒸汽，用以加熱給水。這個過程也受散熱等環境溫度的影響。在超高壓機組中還采用再熱循環，即把做過一段功的蒸汽從汽輪機的高壓缸的出口將做過功的蒸汽全部抽出，送到鍋爐的再熱汽中加熱后再引入氣輪機的中壓缸繼續膨脹做功，從中壓缸送出的蒸汽，再送入低壓缸繼續做功。流入和流出的蒸汽在每個階段都必須保持一種平衡，此外，由于設備之間的耦合不可能做到完全密封，在鍋爐循環做功期間，總會有一些水丟失，為了保持平衡，還需不斷的補水。在補水的過程中也會受到補給水的溫度和量的多少等不確定性因素影響。

綜上所述，燃料對鍋爐加熱，是熱能不斷轉化為機械能，再轉化為電能的過程。而熱能由于環境、海水和湖泊水的溫度，補給水的溫度以及蒸汽的循環等不確定性因素的影響，將會對煤耗成本產生影響。若系統較鍋爐理想循環狀態下丟失熱能較多的話，從而將增加燃料成本，這個增加的燃料成本稱為“不確定損耗成本”。這個“不確定損耗成本”將會對經典經濟調度模型的誤差進行補償。

本文的目標是為了降低單位發電成本，即減少燃料成本占發電總量的比例。由于電力供需平衡的約束，所以發電總量是恒定的。因此，對于每臺發電機的“不確定損耗成本”而言，將其表示成與發電機出力有關的線性函數，即

式中：PGi為第i臺發電機的出力；ΔF（PGi）為第i臺發電機的“不確定損耗成本”；ξi、λi為不確定參量，ξi∈U，λi∈V，其集合U和V在后面描述。

2 線性魯棒優化理論

2.1 線性魯棒優化模型

20世紀70年代Soyster提出線性規劃魯棒優化模型[11]，魯棒優化是解決內部結構和外部環境不確定情況下的優化方法。魯棒優化解決內部結構變動問題時，對于數學規劃問題而言，一種是約束條件參數的不確定性，一種是目標函數參數的不確定性[12]，本文的問題是目標函數參數的不確定性。

魯棒優化已經從Soyster的線性優化魯棒方法，發展到目前魯棒優化理論的經典體系。有些學者在建立魯棒優化理論方面進行了重要工作，他們研究的是具有不同形式的數據不確定性的線性規劃問題、二次規劃問題和半定規劃問題等。本文涉及到線性魯棒優化問題[10～12]。

一般魯棒優化定義為

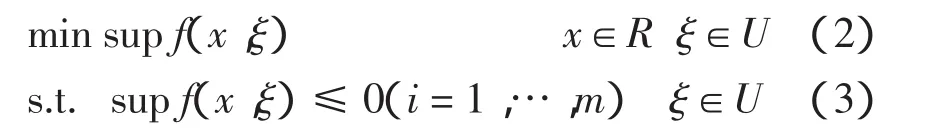
線性規劃定義為

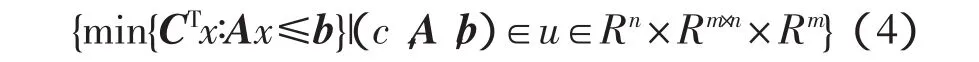
記A={a1，a2，…，an}，b={b1，b2，…，bn}其中ai為約束矩陣A的第i行，則式（4）可寫為

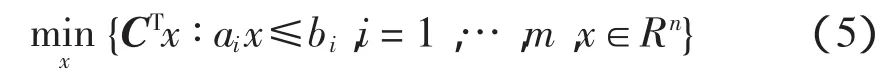
假設a1∈U，a2∈U，an∈U，其中Ui（i=1，…，m）為不確定集合，目標函數中系數C的不確定性可以歸納為約束矩陣的不確定性。則式（5）魯棒對應：

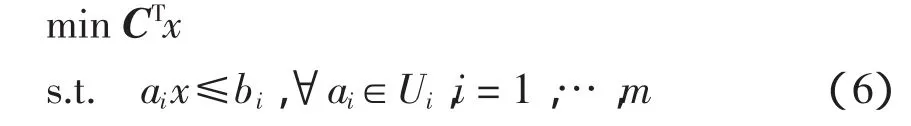
易知aix≤bi，?ai∈Ui，i=1，…，m，等價于求解問題。

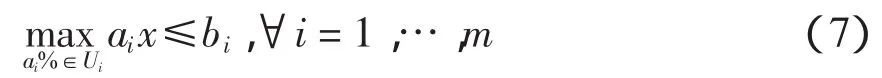
式（7）問題的復雜性決定魯棒優化問題的復雜性。

2.2 集合U的確定與計算原則

魯棒優化問題的關鍵是不確定集合U的確定以及在某給定U下復雜min-max模型的化簡，實際計算的可操作性，本文考慮“盒式”不確定集合，即設參數U的形式為

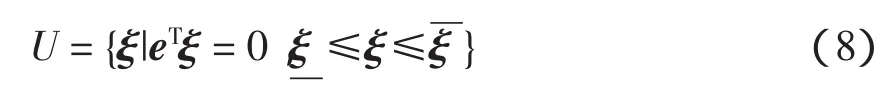
Soyster針對一般線性規劃模型的約束矩陣列的不確定性，設計了一套魯棒優化方法。首先，對于任意一個不確的數據元素，設計基于數據元素的標稱值的一個可能的有界對稱區間，通過引入隨機變量消除標稱值，使得數據元素變成完全不確定的，然后，在原來的線性規劃模型的基礎上，對每個不確定數據元素引入決策變量，在標準形式的約束方程的左端添加不確定性數據的最大值與引入變量的乘積。這樣，原問題的魯棒對應仍然是線性規劃問題，但消除了數據元素的不確定性[3]。這樣，就可以用一般的方法來解決本文的問題。

3 模型的建立

基于以上描述，假定電網中有NG臺發電機為PGi，i=1，2，…，NG是發電機的節點，在本文的優化問題當中PGi為決定變量，對于每臺發電機而言，發電機的燃料成本是二次函數，故結合所描述的“不確定損耗成本”建立以降低發電成本為目標的函數，即

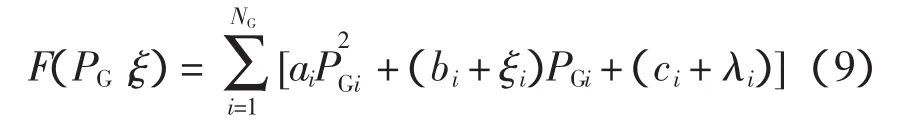
式中：ξi（i=1，2，…，NG）為不確定的變量，表示成向量為ξ=[ξ1，ξ2，…，ξNG]T；PGi為第i臺發電機出力。

在電力系統中還有一些約束，如發電機運行約束、功率平衡約束、線路容量約束等，其限制約束方程∏為

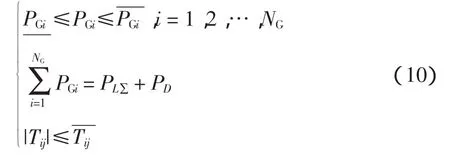
以上的限制都是線性與非線性的集合，因此目標函數是不確定性的最小優化問題，即

結合式（8）、式（11）又可以進一步等效為

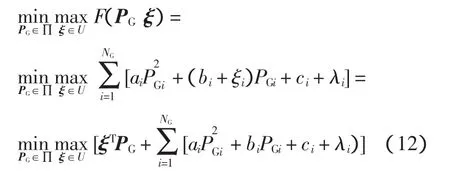
式中，向量PG=[PG1，PG2，…，PGNG]T。

先關注里層優化：

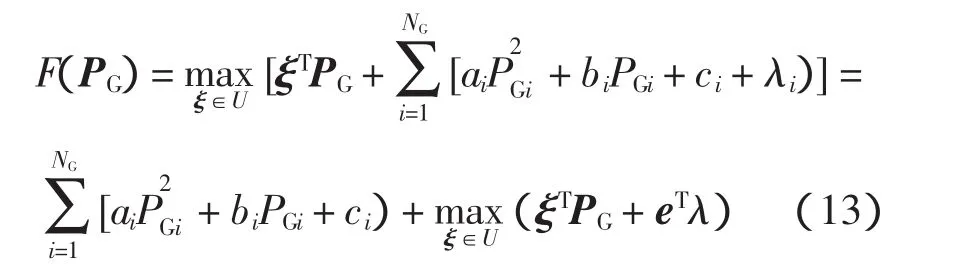
求導后得

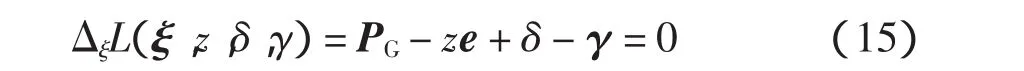
又

根據強對偶定理有

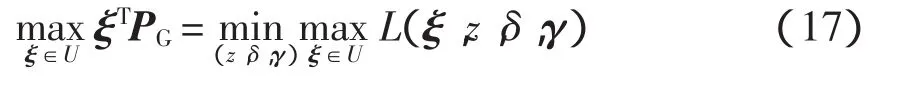
本文主要探討不確定性因素對發電機出力的影響，在式（13），eTλ顯然與單元機組對整個成本的優化無影響，故令其為0，綜合式（12）、式（13）、式（16）及式（17）可把目標函數式（11）整理成

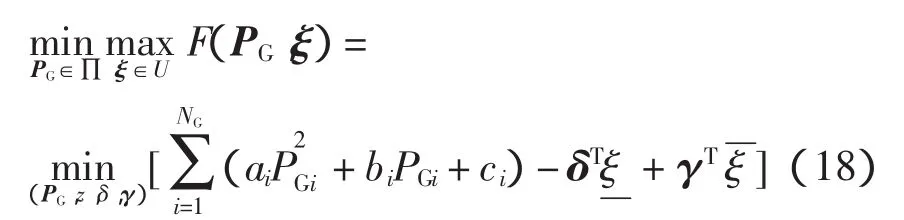
結合式（4）可得式（12）的約束方程

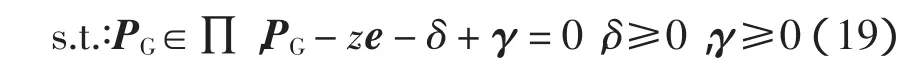
綜上所述，原目標函數式（11）中含有一個不確定變量ξ，通過對不確定變量ξ設置一個如式（8）的“盒式”集合，再依文獻[3]的計算原則，通過數學變換，使得原問題變成了一個普通的單層優化問題，可以用常規的非線性方法進行解答。

4 數值仿真

1）仿真系統

為驗證本文所建模型和算法的有效性，本節對修改后的IEEE 30節點系統進行數值測試，網絡的負荷、發電機的數據、二次成本函數等見文獻[4]，單位為￡/h。為了方便起見，有關發電機的數據重新列在表1中。

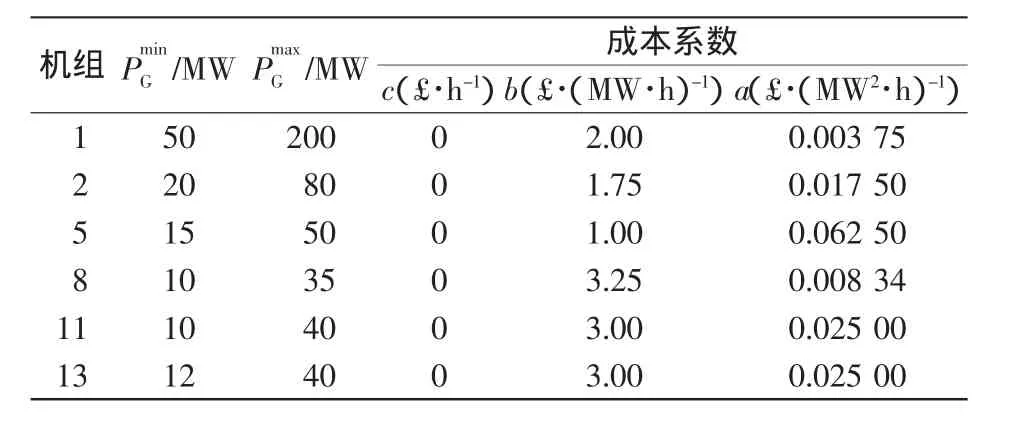
表1 發電機參數Tab.1 Generator parameters

2）最優解PG的擾動情況

由于環境等不確定性影響相對整個鍋爐系統的熱能交換來說，不確定性的變化量不大，本文以系數波動在1%的范圍內來考慮，文中參數ξ取bi值的1%，即

圖1～圖6顯示出各機組出力隨著n的變化而波動，其中，縱坐標表示各機組輸出的實際發電量，橫坐標表示在不同的n值下，發電機波動的百分數（圖中n=1代表波動為0.05%bi）。

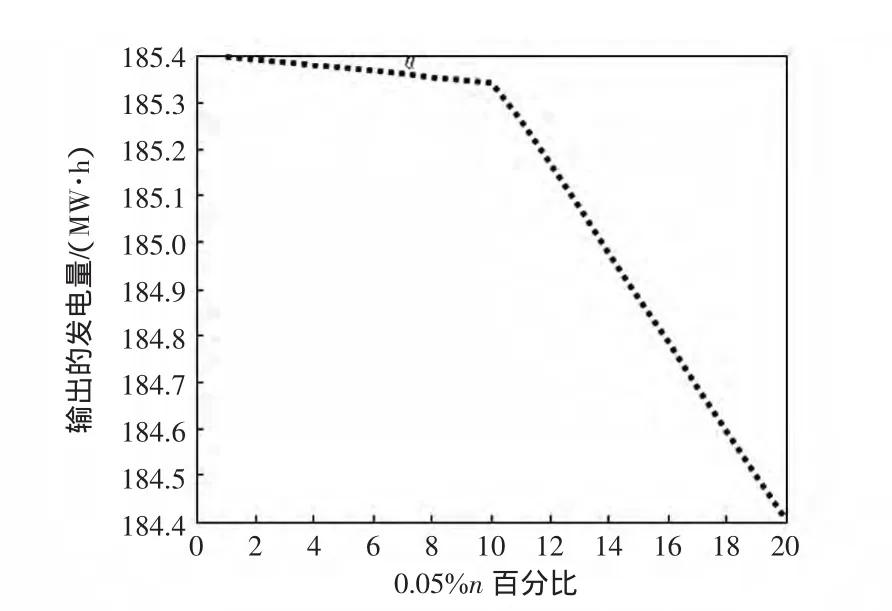
圖1 隨n的變化機組1的出力變化Fig.1 Outputofbus1w ith the change n

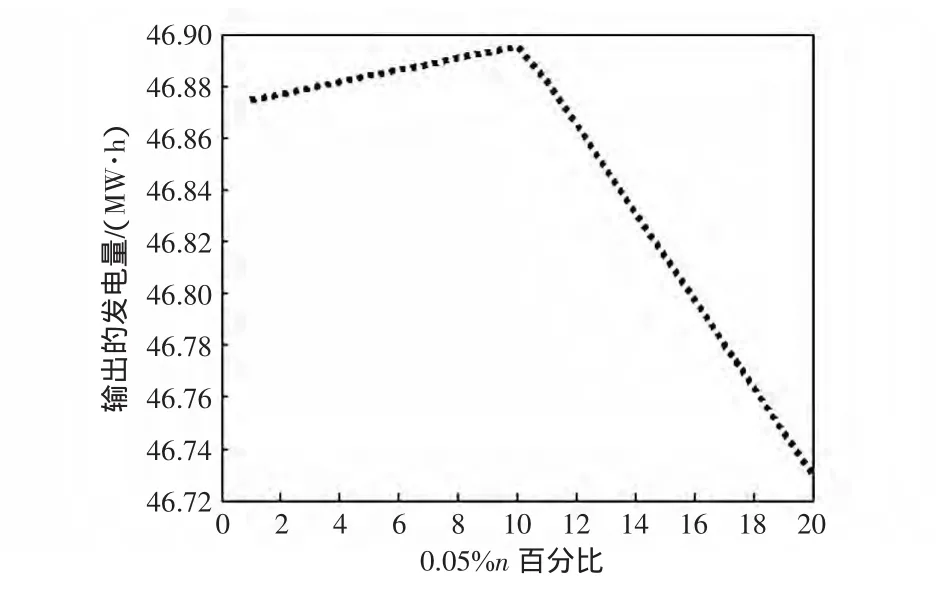
圖2 隨n的變化機組2的出力變化Fig.2 Outputofbus2w ith the change n

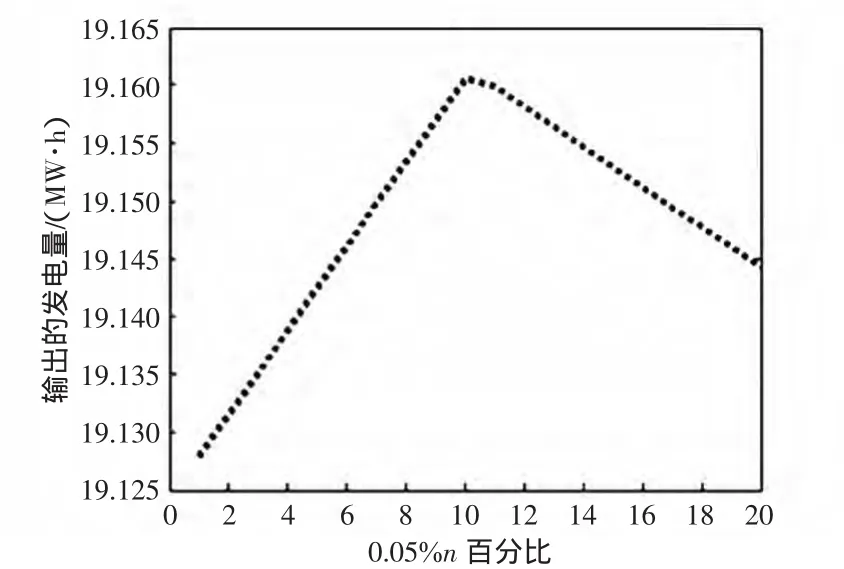
圖3 隨n的變化機組5的出力變化Fig.3 Outputof bus5w ith the change n

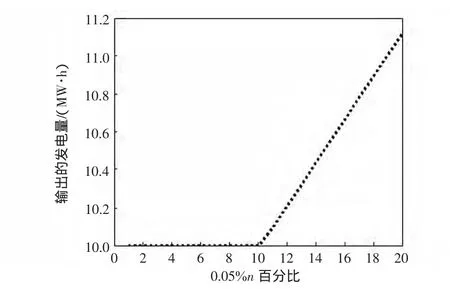
圖4 隨n的變化機組8的出力變化Fig.4 Outputof bus8with the change n

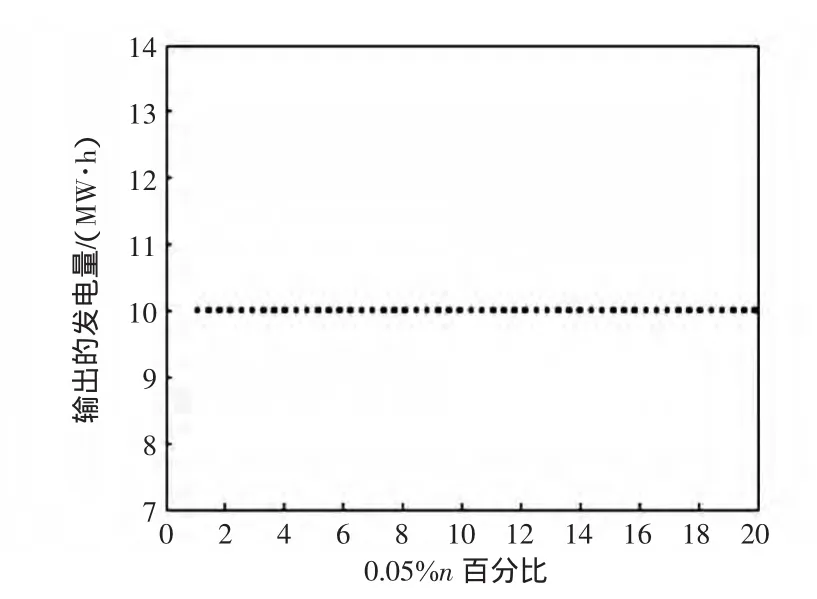
圖5 隨n的變化機組11的出力變化Fig.5 Outputof bus11w ith the change n

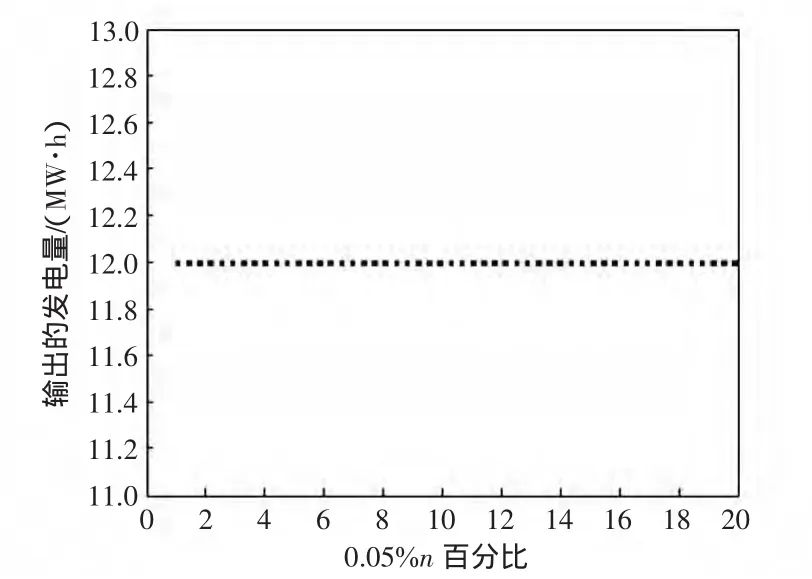
圖6 隨n的變化機組13的出力變化Fig.6 Outputof bus13w ith the change n

圖7 隨n的變化發電成本的變化Fig.7 Generating cost with the change n

通過觀察和比較各仿真圖，易知發電成本函數的不確定性對調度機組的最優出力將有一定的影響，并且隨著不確定性值的增大（即n增大），各機組最優出力將需要重新進行調整使得成本函數達到最優值。由圖1～圖7可以看出，不是所有的機組都隨n的增大而改變，有些機組隨n的增加先增大機組出力然后又減小，有些機組卻先不改變出力而后隨n的增加而增加機組出力，其中機組11和13在限制性的條件下保持最小機組出力而不改變，機組的出力隨n的改變并沒有確定性的規律，但是從圖7可以看出，隨著n增加到20的時候其發電成本卻一直在增長，由此可以看出，通過有效抑制減少鍋爐系統相對理想狀態下不確定量的變化幅度將會節省成本，提高利潤。這就促使發電廠商去對各電廠進行技術改造以提高經濟效益，可以從機組蒸汽溫度的冷凝，煤質以及更新已經老化的機組等去考慮。

表2給出了采用本文模型所得到的機組最優分配值與最小成本。通過表2可以看出，獨立系統運行員（ISO）可以根據系統運行的實際情況（如環境影響、海水溫度影響等）合理確定系統擾動指標進行經濟調度，在不同的擾動指標下得出的經濟調度值可以作為ESD問題的最優解與次優解，這種調度方式顯示了本文模型優于傳統ESD模型最優解的唯一性。對在不考慮擾動的情況下用本文的數據進行最優化的調度計算，其最優值與擾動為0.05%所得出的經濟調度最優值非常接近，而擾動值偏大的時候，就有偏差，這可從表1中不同擾動的大小看出。此外，從表1中可看出，擾動越大，發電成本將逐步增加，這就促使人們盡量抑制不確定因素對系統的影響，使擾動值降低可減少成本。系統的不確定性肯定是存在的，這就促使當值調度員選擇合理的擾動指標，使系統在最經濟的情況下運行。

表2 發電機組最優分配值與最小成本Tab.2 Optimal allocation value and the minimum cost of generation

當前各國大部分經濟調度模型都是使用大型線性規劃的有功（直流）最優潮流模型，若能在經濟調度模型中考慮不確定性因素所帶來的“不確定損耗成本”的影響，這樣更能在調度的時候對機組出力進行合適的變化，可以提高經濟效益。

5 結語

本文利用魯棒優化的方法來解決機組在運行過程中受到不確定性因素的影響而帶來的附加成本，在實際的經濟調度和促使發電廠進行技術改造有理論和指導作用，本文模型較傳統的經濟調度模型有一定的優勢，考慮了不確定性因素的影響，可以更好地指導調度員進行經濟調度，從而保證更大的利潤空間，有一定的應用價值。另外，本文提出的方法還可以用來解決在最優潮流或經濟調度中在未知負荷分布的情況下利用已有的數據對負荷不確定性進行計算。需要進一步研究的是需要尋找一種更有效的方法來處理電力系統不確定性的影響，獲得更加精確的結果。本文的仿真計算表明該方法的可行性和有效性。

[1]譚濤亮，張堯（Tan Taoliang，Zhang Yao）.計及直流控制方式轉換和換流變變比調整的交直流潮流算法研究（Study on AC/DC power flow algorithm considering the switching of DC control mode and converter transformer ratio）[J].電力系統保護與控制（Power System Protection and Control）2011，39（1）：40-45，52.

[2]任麗佳，江秀臣，曾奕（Ren Lijia，Jiang Xiuchen，Zeng Yi）.提高輸電線路輸送容量DLR系統的相關理論研究（Theoretical research on dynamic line rating system for improving transmission capacity of overhead line）[J].高壓電器（High Voltage Apparatus），2008，44（3）：250-253.

[3]顧承紅，艾芊（Gu Chenghong，AiQian）.基于改進內點法的含風電場的系統最優潮流計算（Optimal power flow calculation based on the improved interior method for a system integrated with wind farms）[J].中國電力（Electric Power），2007，40（1）：89-93.

[4]張小平，陳朝暉（Zhang Xiaoping，Chen Zhaohui）.基于內點法的安全約束經濟調度（Security-constrained economic dispatch through interior point methods）[J].電力系統自動化（Automation of Electric Power Systems），1997，21（6）：27-29，54.

[5]郭志東，徐國禹（Guo Zhidong，Xu Guoyu）.用二次規劃法解算互聯系統經濟調度（Calculation of economic dispatch of interconnected system using quadratic programming）[J].電力系統自動化（Automation of Electric Power Systems），1998，22（1）：40-44.

[6]王功濤（Wang Gongtao）.電力市場條件下基于模式識別和逐次線性規劃技術的安全約束調度研究（A Study on Security Constrained Dispatching Based on Pattern Recognition and Successive Linear Programming Techniques in the Power Market Environment）[D].北京：中國電力科學研究院（Beijing：Electric Power Research Institute of China），2002.

[7]秦梁棟（Qin Liangdong）.基于Queen-bee進化的遺傳算法在電力系統經濟調度中應用（Queen-bee evolution based genetic algorithm to economic dispatch）[J].電力系統自動化設備（Electric Power Automation Equipment），2005，25（5）：64-66.

[8]葉彬，長鵬翔，趙波，等（Ye Bin，Chang Pengxiang，Zhao Bo，et al）.多目標混合進化算法及其在經濟調度中的應用（Multiobjective hybrid evolutionary algorithm for economic load dispatch）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2007，19（2）：66-72.

[9]丁曉群，蔡志慧（Ding Xiaoqun，CaiZhihui）.人工神經網絡在電力系統中的研究與應用現狀（Artificial neural network in power system research and application）[J]．水利水電科技進展（Advances in Science and Technology of Water Resources），1996，16（4）：12-16.

[10]Xiao Fei，Mc Calley JD．Risk-based security and economy trade off analysis for real-time operation[J]．IEEE Trans on Power Systems，2007，22（4）：2287-2288．

[11]Wang Jianhui，Shahidehpour M，Li Zuyi.Security-constrained unit commitment with volatile wind power generation[J].IEEE Trans on Power Systems，2008，23（3）：1319-1327.

[12]Yan Yong，Wen Fushuan，Yang Shouhui，et al.考慮風電出力波動性的發電調度（Generation scheduling with fluctuating wind power）[J].電力系統自動化（Automation of Electric Power Systems），2010，34（6）：79-88.

[13]徐家旺，黃小圓（Xu Jiawang，Huang Xiaoyuan）.魯棒優化及其應用研究的進展（Advance in research on robust optimization and application）[C]//中國控制與決策學術年會（Chinese Control and Decision Conference）.哈爾濱（Haerbin），2005.

[14]李彩華，郭志忠，樊愛軍（LiCaihua，Guo Zhizhong，Fan Aijun）.電力系統優化調度概述（I）——經濟調度與最優潮流（Summary of power system optimal dispatch（I）--Economic dispatch and optimal power flow）[J]．電力系統及其自動化學報（Proceedings of the CSU-EPSA），2002，14（2）：60-63.

[15]Xiao Fei，Mc Calley JD．Risk based multi-objective optimization for transmission loading relief strategies[C]//IEEE Power Engineering Society General Meeting，Tampa，USA：2007．