基于IDA-PBC的LCL濾波并網逆變器控制
李敏,徐群
(河海大學能源與電氣學院,南京 211100)
并網逆變器作為分布式發電系統的核心部分,近年來得到了廣泛關注[1~3];其輸出電流的總諧波畸變THD(total harmonic distortion)是衡量并網發電質量的重要技術指標,為此常采用LCL濾波器濾除由開關造成的各次諧波。相比于L或LC濾波器,LCL濾波器具有三階的低通濾波特性,對于同樣的諧波標準和較低的開關頻率,可以采用相對較小的電感設計,有效減小了系統的體積并降低了損耗。同時,LCL濾波器的網側電感與電網電抗相串聯,能夠減小電網電抗的變化對系統的影響。然而,LCL濾波器增加了系統的階數且存在固有諧振峰,易引起系統輸出振蕩,對并網逆變系統電流控制器的設計有更高的要求。傳統的電流跟蹤控制策略主要集中在雙閉環電流控制[4~6]、零極點配置控制[7]、最優控制[8~9]和重復控制[10~11]等方法上。上述方法由于建立在經典控制理論的傳遞函數方法上,總是存在諸如參數計算或整定過于復雜、魯棒性不強等缺點。文獻[12]提出了一種多諧振滑模控制器,消除了抖振問題,能夠高精度地跟蹤參考電流并保證了較強的魯棒性,但局限于單相系統。文獻[13]將L2增益魯棒控制方法應用于三相LCL濾波并網逆變系統中,即使在電網電壓畸變不平衡情況下也有較好的諧波電流抑制能力,但該方法的前提是在電容支路串入電阻,增加了系統的損耗。
無源控制理論從系統的能量角度出發,物理意義明確,可實現系統的漸進穩定,且對參數攝動和外界擾動具有較強的魯棒性;互聯與阻尼配置無源控制IDA-PBC(interconnection and damping assignment passivity-based control)作為哈密頓系統的一種新型無源控制設計理論,已成功應用于各類電力電子裝置中[14~17]。文中首先介紹了IDA-PBC的基本原理,建立了三相LCL濾波并網逆變系統的端口受控哈密頓PCHD(port controlled Hamiltonian with dissipation)數學模型,然后基于間接控制的思想設計了IDA-PBC控制器,并驗證了閉環系統在平衡點處的漸進穩定性,最后在電磁暫態綜合分析程序PSCAD/EMTDC中仿真驗證了該控制策略的正確性、有效性與魯棒性。
1 IDA-PBC的基本原理
考慮端口受控的耗散哈密頓系統
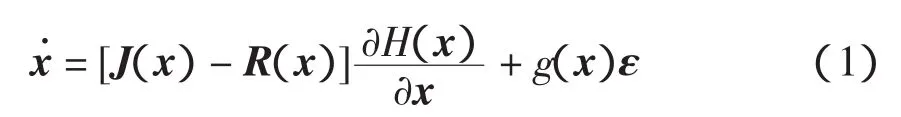
式中:J(x)為反對稱矩陣,反映了系統內部的互聯特性,滿足J(x)=-J(x)T;R(x)為對稱半正定矩陣,反映了系統的耗散特性;H(x)為哈密頓函數;向量ε反映了系統與外部的能量交換。
由IDA-PBC定理[18]可知,給定J(x)、R(x)、H(x)、g(x)和期望穩定的平衡點x*∈Rn,若能找到函數Ja(x)、Ra(x)和一個向量函數K(x)滿足
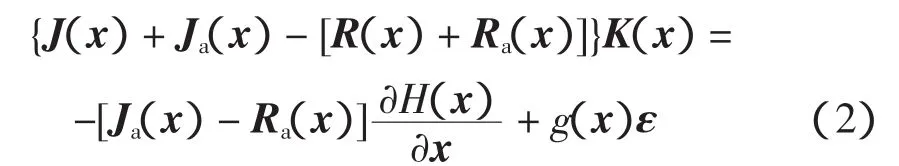
且使得如下條件成立:
(1)結構守恒,即

(2)可積性,即K(x)是標量函數的梯度,滿足
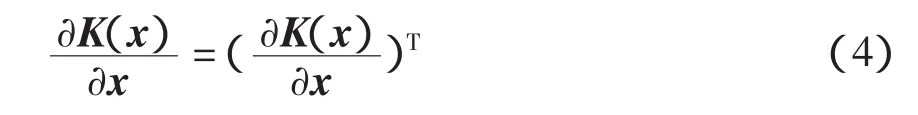
(3)在期望平衡點x*處,K(x)滿足

(4)Lyapunov穩定性,即在x*,K(x)的雅可比滿足
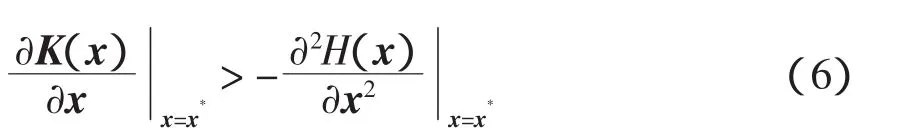
則平衡點x*為閉環系統的一個穩定平衡點,且閉環系統可表示為
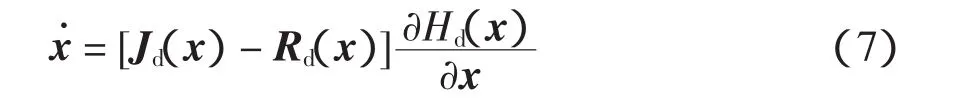
其中
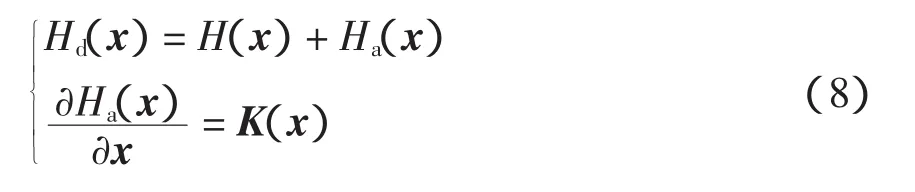
2 系統PCHD模型
三相LCL濾波并網逆變器的典型拓撲如圖1所示。其中:Udc為直流側電源電壓,一般情況下可作為光伏電池和風電機組整流端的接口;電感L1、L2和電容C組成輸出濾波器;R1、R2分別為L1、L2的等效電阻;i1j、i2j分別為LCL濾波器逆變器側和網側電流;uCj為電容C上的電壓;uSj為電網電壓,j=a,b,c。

圖1 LCL濾波并網逆變器的典型拓撲Fig.1 Topology of grid-connected inverter with an LCL filter
將主電路開關元件視作理想開關,根據基爾霍夫回路KVL定律和節點KCL定律,LCL濾波三相并網逆變系統在同步旋轉dq坐標系下的狀態平均模型為
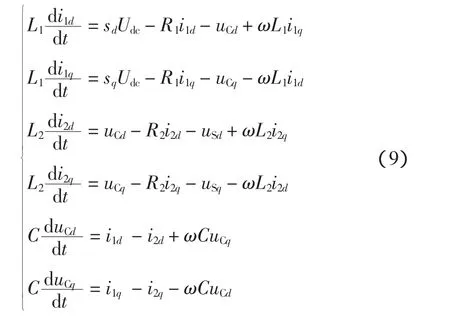
式中:sd、sq為開關函數在dq坐標系下的分量。
定義系統的狀態變量為
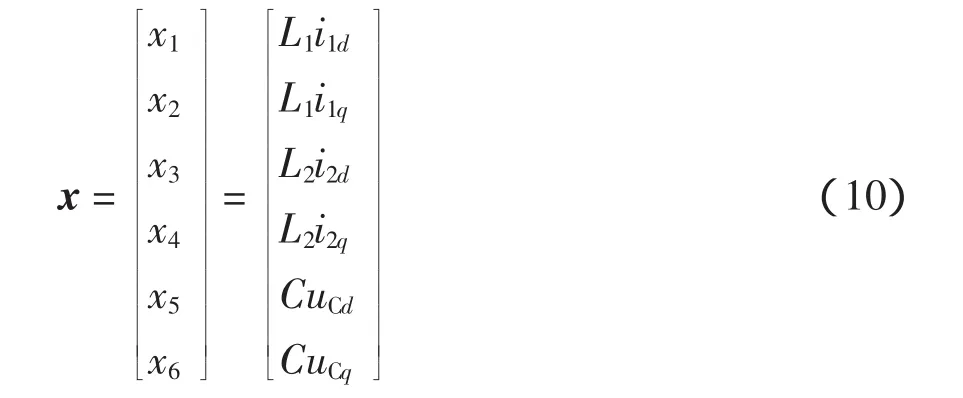
選取系統的哈密頓函數為
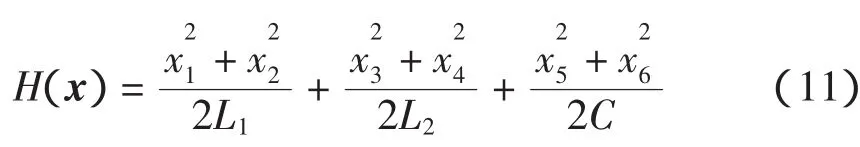
H(x)反映了系統儲能元件中的能量,具有明確的物理意義。
將系統表示為PCHD形式,各矩陣的具體表達式為

首先對系統的無源性進行驗證,定義系統的輸出為

則有如下耗散不等式成立
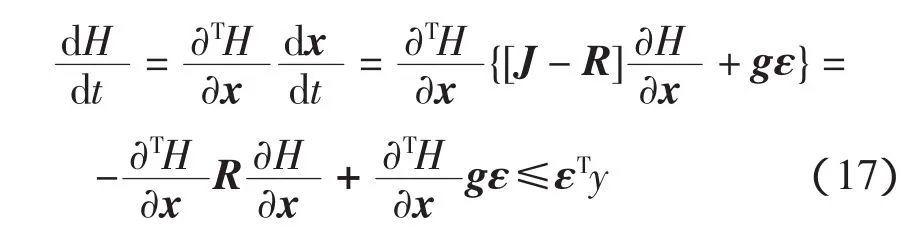
這說明系統能量的增長率總是小于外部注入到系統能量的供給率,即并網逆變系統是無源的。
3 IDA-PBC控制器設計
式(9)描述的系統為典型的欠驅動系統,可基于間接控制的思想通過控制狀態x3→x3*和x4→x4*使狀態x1、x2、x5和x6漸進跟蹤其參考值,最終實現x→x*。
采用自然互聯和注入阻尼的控制方式,即令
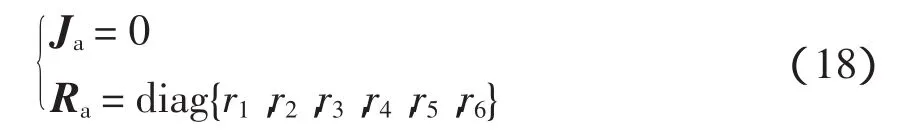
為簡化控制器的設計,設K(x)為常數,結合條件(3),K(x)各分量可依次取為
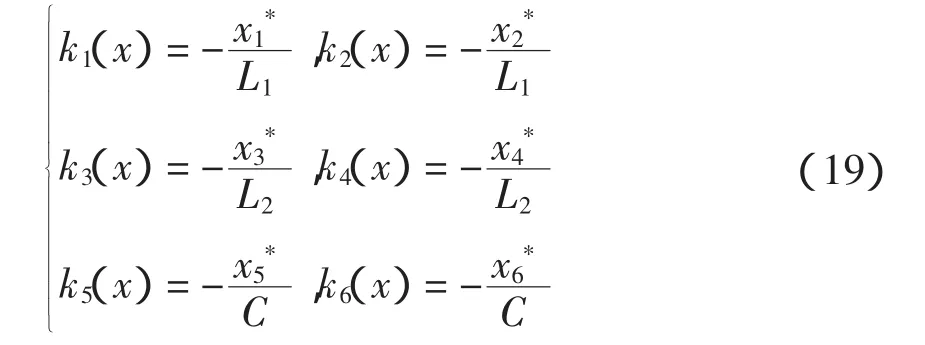
將Ja、Ra和K(x)的值代入式(2),可得系統欠驅動狀態變量的參考值為
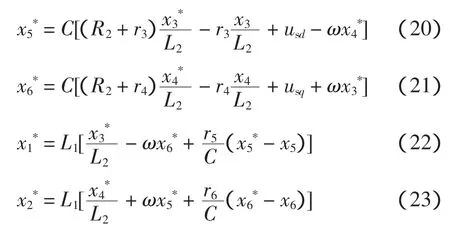
為實現輸出功率對指令有功無功的跟蹤,采用文獻[19]提出的參考電流計算方法,即
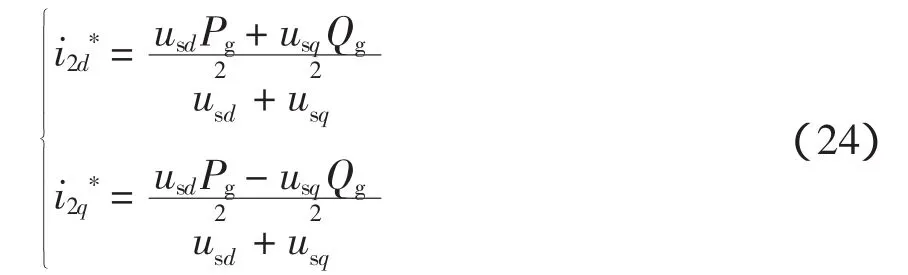
式中,Pg、Qg分別為給定的并網有功、無功功率。
為消除電網電壓畸變時其諧波分量給參考并網電流帶來的影響,利用低通濾波器濾除usd、usq中可能存在的周期分量,即可保證并網電流的諧波含量始終滿足要求。
綜上,可得系統控制律為
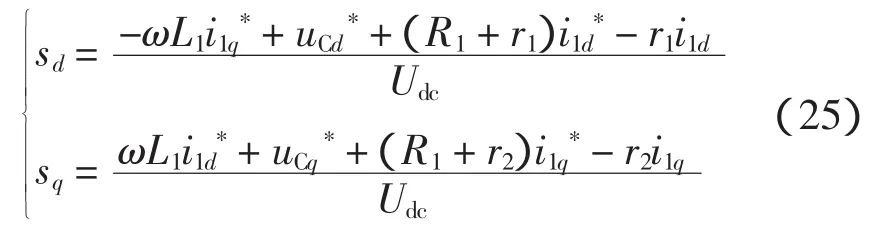
基于以上分析,所設計的IDA-PCB控制器框圖如圖2所示。
進一步驗證閉環系統的漸進穩定性:
將K(x)的值代入式(8),可得通過控制作用注入到系統的能量為
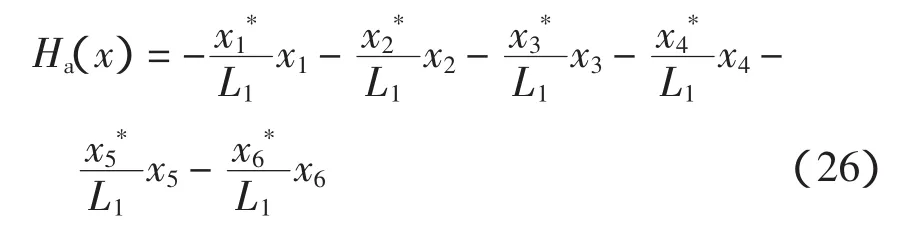
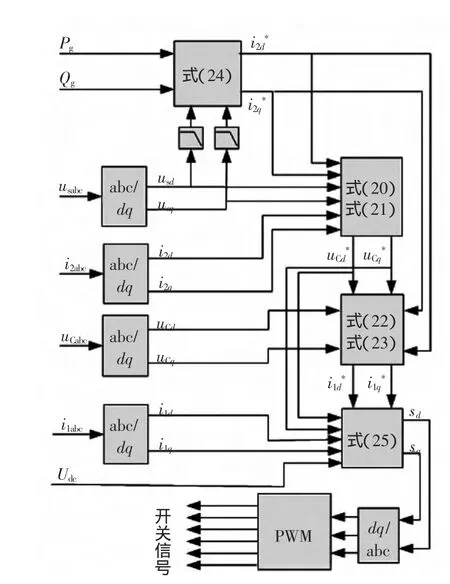
圖2 IDA-PBC控制器框圖Fig.2 Structure of IDA-PBC controller
進而可知閉環系統的哈密頓函數為

由于海森矩陣
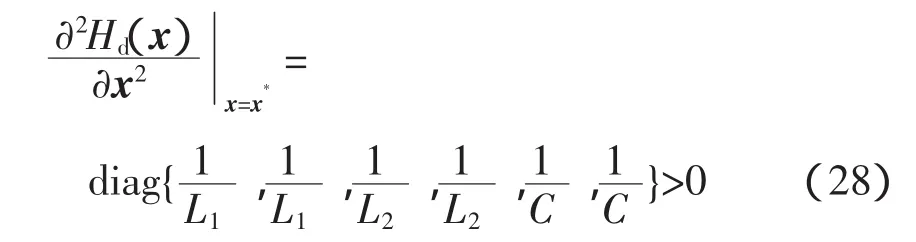
滿足條件(4),所以Hd(x)在x*處存在最小值。又有
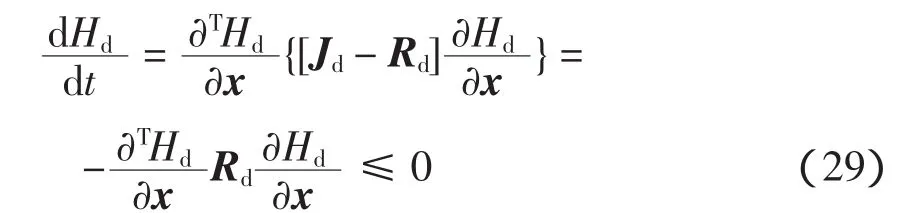
且除了x*以外,沒有任何解x(t)可滯留在集合{x|x∈Rn=0}中。由LaSalle不變集定理[20]可知x*是系統漸進穩定的平衡點。
從理論上保證了閉環系統的穩定性后,還需考慮注入阻尼大小對系統動靜態性能的影響。r1、r2越大,系統收斂速度越快,對外界干擾和參數攝動所造成的跟蹤誤差的抑制效果也越好;但過大會出現過調制現象,系統將產生大量高次諧波。雖然系統中加入了限幅控制,但過大的r1、r2仍然會給系統帶來不利的影響。在保證了快速動態響應的前提下,較小的r3~r6能夠得到更精確的狀態平衡點,穩態精度更高。遵照上述基本原則,再結合仿真模型,即可得到較合適的阻尼系數。
4 仿真實驗研究
為了驗證所提控制策略的有效性,在電磁暫態綜合分析程序PSCAD/EMTDC中建立了圖1所示的系統模型,控制器如式(25)和圖2所示。取阻尼系數Ra=diag{100,100,0.1,0.1,0.1,0.1},LCL濾波器參數按照文獻[21~22]進行設計,如表1所示。

表1 系統仿真參數Tab.1 Parameters for system simulation
4.1 理想電網情況系統動態響應特性分析
首先分析理想電網情況下的系統動態響應特性。設置電網電壓有效值為220 V,頻率為50 Hz。給定并網無功功率Qg始終為0,有功功率Pg在0.02 s時從0階躍變化到2 kW,在0.07 s時階躍到10 kW,在0.15 s時階躍到2 kW。圖3(a)給出了并網電流波形,可以看到,并網電流畸變很小且波形光滑;給定功率發生突變時,系統僅需2~3ms即能無振蕩進入下一個穩態。圖3(b)給出了并網功率瞬時值結果,可以看到,系統功率因數接近為1,由于電容支路未串入阻尼電阻,功率波動更小。圖3(c)給出了并網電流總諧波畸變率的瞬時值結果,即使在并網電流有效值很小的情況下(2.1A),THD值也能保持在1%以下。圖3(d)給出了并網電流0.2 s時基波與各次諧波均方根分布值,由于采用了注入虛擬阻尼的控制方式,很大程度上削弱了系統在諧振頻率(35次諧波)處的諧振。表2給出了IEEE 1574標準對并網電流奇數次諧波最大含有率的要求,仿真結果表明并網電流諧波含量符合該標準。
4.2 畸變不平衡電網情況系統動態響應特性分析
為了驗證所提控制策略的魯棒性,進一步分析電網電壓畸變不平衡情況下系統的動態響應特性。仿真條件設置如下:電網電壓不平衡度為13%,5次諧波含量為5%,7次諧波含量為2%。給定并網無功功率Qg始終為0,有功功率Pg在0.02 s時從0階躍變化到7 kW,系統動態響應波形如圖4所示。
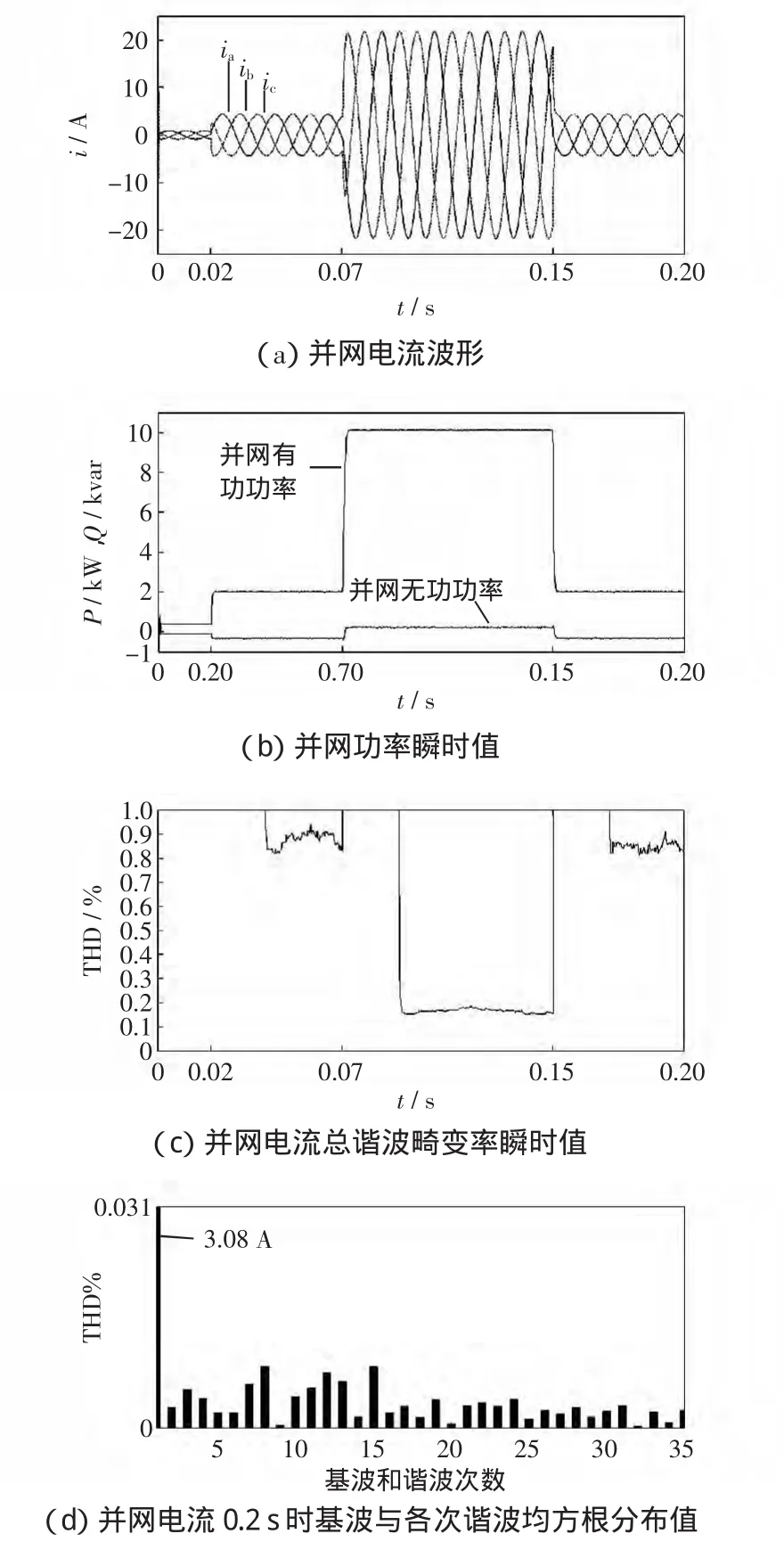
圖3 理想電網情況下的系統動態響應波形Fig.3 System performance under ideal grid voltage condition
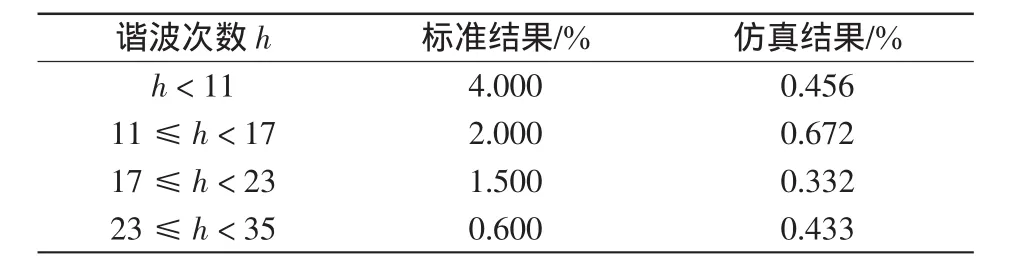
表2 并網電流最大諧波含有率的IEEE 1547標準與仿真結果Tab.2 IEEE1547 standards for harmonics compared with simulated results of grid-connected current
從仿真結果可知,并網電流能夠保持較好的正弦特性;由于電網電壓諧波分量的影響,并網電流的5次和7次諧波分量有明顯的增加,但THD值仍小于1.5%。由于電網電壓負序分量的存在,并網無功和有功功率均出現了2倍電網頻率的大幅脈動。
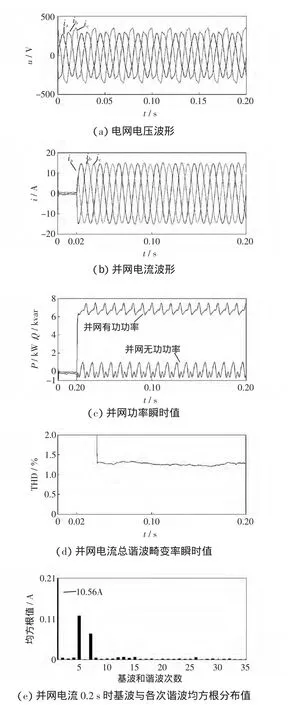
圖4 電網電壓畸變不平衡情況下的系統動態響應波形Fig.4 System performance under distorted and unbalanced grid voltage conditions
6 結論
(1)針對LCL濾波三相并網逆變系統電流控制器難設計的問題,提出了一種基于互聯與阻尼配置的無源控制策略,仿真結果證明該方法能夠以較高的穩態精度和較快的動態響應速度跟蹤參考電流,并網功率波動小,在電網電壓畸變不平衡的情況下,依然有較強的諧波電流抑制能力,魯棒性強。該方法實現簡單,具有一定的工程價值。
(2)對風光并網逆變這類需要保證并網有功功率恒定的系統而言,并網功率的波動會影響其效率與穩定性,甚至使系統無法正常工作。文獻[23]針對該問題提出了一種新的控制策略,通過對電網電壓正序和負序分量的準確估計,計算出電網電壓畸變不平衡情況下系統輸出恒定有功功率對應的并網電流參考指令,最終實現系統輸出恒定有功功率,同時并網電流諧波含量滿足IEEE Std.929—2000標準。如何將該方法或其改進融入到本文所提控制策略中,是今后研究的方向。
[1]李晶(Li Jing).分布式發電系統并網逆變器的無功控制策略(Reactive power control of grid-connected converter in distributed generation system)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),2011,23(1):155-159.
[2]王成山,李琰,彭克(Wang Chengshan,LiYan,Peng Ke).分布式電源并網逆變器典型控制方法綜述(Overview of typical control methods for grid-connected inverters of distributed generation)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA),2012,24(2):12-20.
[3]Golbon N,Moschopoulos G,Khajehoddin SA.A control strategy for a solar grid-connected inverter[C]//26th Annual IEEE Canadian Conference on Electrical and Computer Engineering.Regina,Canada,2013.
[4]胡雪峰,韋徵,陳軼涵,等(Hu Xuefeng,WeiZheng,Chen Yihan,et al).LCL濾波并網逆變器的控制策略(A control strategy for grid-connected inverters with LCL filters)[J].中國電機工程學報(Proceedings of the CSEE),2012,32(27):142-148.
[5]徐志英,許愛國,謝少軍(Xu Zhiying,Xu Aiguo,Xie Shaojun).采用LCL濾波器的并網逆變器雙閉環入網電流控制技術(Dual-loop grid current control technique for grid-connected inverter using an LCL filter)[J].中國電機工程學報(Proceedings of the CSEE),2009,29(27):36-41.
[6]Liu Fei,Zhou Yan,Duan Shanxu,et al.Parameter design of a two-current-loop controller used in a grid-connected inverter system with LCL filter[J].IEEE Trans on Industrial Electronics,2009,56(11):4483-4491.
[7]XueMingyu,Zhang YU,Liu Fangrui,et al.Optimized pole and zero placement with state observer for LCL-type grid connected inverter[C]//IEEE Energy Conversion Congress and Exposition.Phoenix,USA,2011.
[8]Tang Hao,Zhao Rongxiang,Tang Shengqing,et al.Linear quadratic optimal control of a single-phase grid-connected inverter with an LCL filter[C]//IEEE International Symposium on Industrial Electronics.Hangzhou,China,2012.
[9]Eren S,Bakhshai A,Jain P.Control of grid-connected voltage source inverter with LCL filter[C]//IEEE Applied Power Electronics Conference and Exposition.Orlando,USA,2012.
[10]王斯然,呂征宇(Wang Siran,LüZhengyu).LCL型并網逆變器中重復控制方法研究(Research on repetitive control method applied to grid-connected inverter with LCL filter)[J].中國電機工程學報(Proceedings of the CSEE),2010,30(27):69-75.
[11]Jiang Shuai,Peng F Z.Repetitive control of grid-connected inverter using a high resonance frequency LCL filter[C]//IEEE Applied Power Electronics Conference and Exposition.Long Beach,USA,2013.
[12]LiuWeizeng,Hao Xiang,Yang Xu,et al.A multi-resonant sliding-mode controller for single-phase grid-connected inverter with LCL-filter[C]//28th Annual IEEE Applied Power Electronics Conference and Exposition.Long Beach,USA,2013.
[13]曾正,楊歡,趙榮祥(Zeng Zheng,Yang Huan,Zhao Rongxiang).LCL濾波并網逆變器的魯棒控制(Robust control strategy for grid-connected inverters with LCL filter)[J].高電壓技術(High Voltage Engineering),2011,37(12):3143-3150.
[14]陳宗祥,劉曉東,潘俊民(Chen Zongxiang,LiXiaodong,Pan Junmin).基于互聯與阻尼配置無源控制的并網逆變器電流控制技術(Current control strategy for grid-connected inverter based on IDA-PBC)[J].電工技術學報(Transactions of China Electrotechnical Society),2011,26(8):99-105.
[15]Bottcher M,Dannehl J,Fuchs FW.Interconnection and damping assignment passivity-based current control of grid-connected PWM converter with LCL filter[C]//14th International Power Electronics and Motion Control Conference.Ohrid,Macedonia,2010.
[16]Serra FM,De Angelo CH,ForchettiDG.IDA-PBC control of shunt active filters for harmonics compensation[C]//IEEE/PES Transmission and Distribution Conference and Exposition.Montevideo,Uruguay,2012.
[17]魯偉,徐長波,李春文(Lu Wei,Xu Changbo,Li Chunwen).并聯混合有源濾波器哈密頓系統建模及無源控制(Hamiltonian modeling and passivity-based control of shunt hybrid active power filter)[J].控制理論與應用(Control Theory&Applications),2012,29(11):1397-1402.
[18]王久和.無源控制理論及其應用[M].北京:電子工業出版社,2010.
[19]曾正,楊歡,趙榮祥,等(Zeng Zheng,Yang Huan,Zhao Rongxiang,et al).基于無源哈密爾頓系統理論的LC濾波并網逆變器控制(A novel control strategy for grid-connected inverters with LC filter based on passive Hamiltonian theory)[J].電網技術(Power System Technology),2012,36(4):207-212.
[20]梅生偉,申鐵龍,劉康志.現代魯棒控制理論與應用[M].北京:清華大學出版社,2008.
[21]張興,曹仁賢.太陽能光伏并網發電及其逆變控制[M].北京:機械工業出版社,2010.
[22]劉飛,查曉明,段善旭(Liu Fei,Zha Xiaoming,Duan Shanxu).三相并網逆變器LCL濾波器的參數設計與研究(Design and research on parameter of LCL filter in three-phase grid-connected inverter)[J].電工技術學報(Transactions of China Electrotechnical Society),2010,25(3):110-116.
[23]郭小強,鄔偉揚,漆漢宏(Guo Xiaoqiang,Wu Weiyang,QiHanhong).電網電壓畸變不平衡情況下三相光伏并網逆變器控制策略(Control strategies of three-phase PV grid-connected inverter under distorted and unbalanced voltage conditions)[J].中國電機工程學報(Proceedings of the CSEE),2013,33(3):22-28.

