GPS高程擬合方法探討

夏永成,樊寬林,劉 非

(四川中水成勘院測繪工程有限責任公司，四川 成都 610072)

1 前 言

利用GPS測量得到的高程是基于WGS-84橢球的大地高。由于我國的高程是正常高系統，是建立在似大地水準面基礎上的，它們之間的關系是：

Hr=H84-ζ

(1)

ζ是該點的高程異常(見圖1)。知道了各點的高程異常就可以求出各點的正常高。

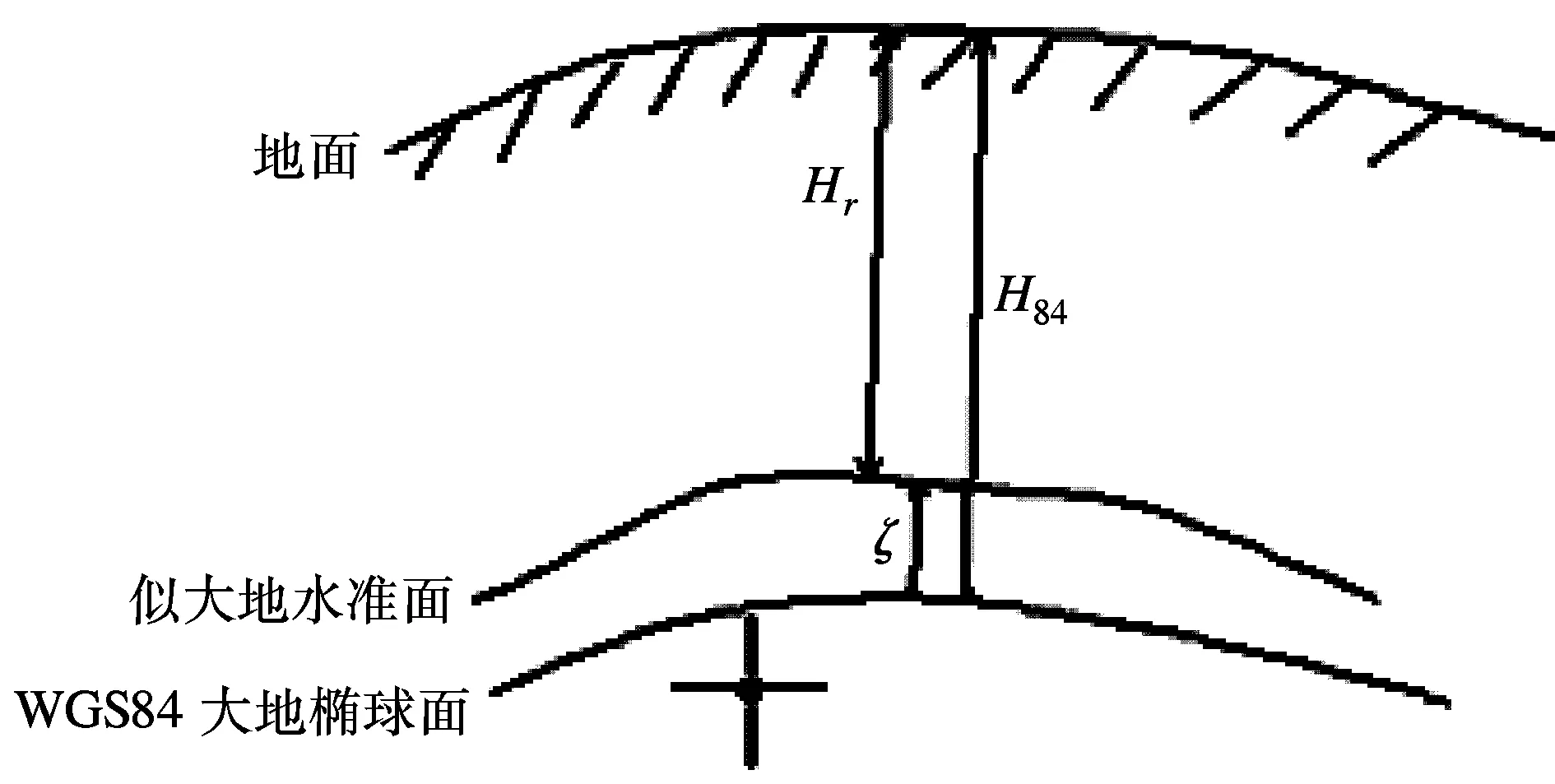
圖1 高程異常示意

目前求解高程異常的方法很多，主要是數值逼近法，分為函數模型逼近和統計模型逼近。函數模型逼近的最大優點是對趨勢性變化效果擬合效果較好；統計模型的特點是計算靈活，對穩態隨機過程的逼近效果較好。常用的函數模型逼近法有解析內插法(包括曲線內插法、樣條函數法和Akima法)、曲面擬合法(包括平面擬合法、多項式曲面擬合法、多面函數擬合法、曲面樣幾條擬合法和移動曲面擬合法)等。還有一些其他方法如：地球重力場法和地形改正法，神經網絡模型法和基于灰色系統理論的灰關聯法等。

2 幾種常用的擬合方法及特點

2.1 多項式擬合法

設點的ζ與點的位置信息(x,y)有以下關系

ζ=f(x,y)+ε

(2)

式中f(x,y)為ζ中趨勢值；ε為誤差。

設f(x,y)=a0+a1x+a2y+a3x2+a4y2+a5xy+…

(3)

寫成矩陣形式有：

ζ=XB+ε

(4)

對于每個已知點，都可以列出以上方程，在ΣεTPε=min的條件下，可以解出

B=(XTPX)-1XTPζ

(5)

再代入式(3)求高程異常，最后按式(1)求出Hr。

2.2 多面函數法

設點的ζ與點的位置信息(x,y)有如下關系

(6)

式中ai為待定系數，Q(x,y,xi,yi)為核函數，xi、yi為已知點坐標。核函數一般選用具有對稱性的距離型即：

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+σ]1/2，

Q(x,y,xi,yi)=[(x-xi)2+(y-yi)2+σ]-1/2

(7)

上兩式分別稱為正雙曲面函數和倒雙曲面函數。σ為光滑系數為一常數，可由試驗給定。

當待求點數等于已知點數時，任一點ζP為

ζP=QPQ-1ζ=(Q1PQ2P…

(8)

式中，Qij=Q(x,y,xi,yi)。當待求點多于已知點數時，

ζP=QP(QTQ)-1ζ

(9)

2.3 移動曲面法

一般對某一內插點，(xj′,yj′),若數據點(xi,yi)滿足

(xi-xj′)2+(yi-yj′)2≤R2

(10)

可用這些數據點參加內插，則稱以(xj′,yj′)為圓心，半徑為R的圓形移動窗口內曲面內插。

設移動到第j個內插點(xj′,yj′)時，利用落入該點移動窗口內的m個數據點(xi,yi)上的觀測值ζi(i=1,2,…m),以下列多項式

ζi=a0+a1x+a2y+a3xy

(11)

計算第j個內插點函數值。在m個數據點上建立如下誤差方程：

令

Vi=a0+a1xi+a2yi+a3xiyi+ζi,Pi

(12)

Pj=diag(P1,P2,…Pm)Xj=(a0,a1,a2,a3)T,

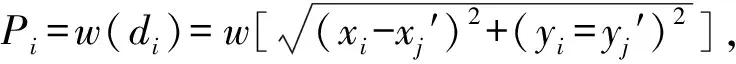
w(d)為權函數，目前廣泛使用的權函數有

w(d)=exp(-d2/a2)

(13)

w(d)=1/(1+d2/a2)

(14)

a為常數，可由試驗給定，一般取數據點平均距離的兩倍。應用最小二乘原理解得

(15)

代入(11)可得該點的高程異常。

移動曲面計算法在計算時，通常采用契比雪夫多項式為移動多項式。

2.4 地球重力場模型法

地球重力場模型是依據重力場理論導出的計算重力異常等的數學模型，它是利用最新的衛星跟蹤數據、地面重力數據、衛星測高等重力場信息計算得到的重力位的球諧函數級數展開的系數[4]。根據給定的重力場模型的位系數Cnm、Snm可用下式計算各點的高程異常：

sinmL)Pnm(sinB)

(16)

式中ρ、B、L——分別為計算點的矢徑、緯度和經度;

GM——為引力常數與地球質量的乘積；

γ——為計算的正常重力值；

a——為參考橢球的長半軸；

Cnm、Snm——為完全規格化位系數；

Pnm(sinB)——為完全規格化締合Legendre函數；

N——為地球重力場模型展開的最大階數；

m——為次。

若給定一組位系數就確定了一個相應的地球重力場模型，就可以求出該點相對于此模型的高程異常。

目前國際上公開的比較有代表性的EGM96模型,它是美國NASA/GS-FC和國防制圖局聯合研制的360階全球重力場模型，相當于全球55Km分辨率。它在美國本土分辨率為50Km，精度達到幾厘米，在我國精度只有米級，因此難以直接應用于生產，但它包含比較準確的重力場長波信息[3]，可用于更高精度的GPS高程擬合。

2.5 各種擬合方法的特點

多項式擬合法是在擬合區域的已知高程點之間按削高補低的原則構造一個多項式曲面(線)擬合區域的似大地水準面。當擬合范圍大，高程異常變化大，擬合的誤差就越大。擬合多項式的階次越高，擬合面產生震蕩的可能性增大。模型的自適應程度較低。

多面函數是一種純數學的逼近方法，它是在待求點上與每個已知點上建立函數關系，這種函數關系表現為一規則的數學曲面，將這些曲面按一定比例迭加起來就可以擬合出任何不規則的曲面。它的核函數是距離的函數，顧及了待求點與已知點之間的相關性，起著權系數矩陣的作用。

移動曲面法用有限區域內所有已知點來擬合該點的高程異常，該區域隨著擬合點的位置變化而移動，可以更好地模擬該區域的似大地水準面。該法精度較高，自適應程度較好[5]。

地球重力場模型法的精度隨著地點的變動而變化，當該區域的所測重力數據沒有參與建模或參與建模的數據少時，計算出的重力異常精度就低，該區域參與建模的重力數據多時精度就高。但利用它計算出的高程異常能準確反應該區域高程異常的變化趨勢。鑒于它們的這些特點，綜合起來衍生出另一種方法——基于地球重力場模型的擬合法。

3 基于地球重力場模型的擬合法

基于地球重力場模型的擬合法把高程異常分為長波信息和短波信息，用地球重力場模型計算長波信息，用逼近函數計算短波信息。它的原理是擬合出用地球重力場模型計算的高程異常誤差的函數，然后用函數計算出的高程異常誤差，再加上該點在地球重力場模型中計算的高程異常。設根據地球重力場模型計算出該點的高程異常為ζGM，該點的高程異常誤差為ε，則有

H84+ζ=H84+ζGM+ε

(17)

移項得

ε=ζ-ζGM

(18)

ζ為該點的實際高程異常。令ε=f(x,y)，f(x,y)為文中所述的擬合函數，利用最小二乘法推估求得內插點的高程異常誤差ε，再代入上式可求得該點的高程異常，最后用高程異常加上該點的大地高得到該點的正常高。這種方法通常被叫做“移去-計算-恢復法”。

4 幾個問題

4.1 參數的選取

在擬合過程中參數的選取是很關鍵的，常見的是以該點的坐標為參數，這樣擬合時所組成的法方程的系數很大，求解待定系數ai的誤差會增大。當用坐標為參數時可以先對它進行中心化，這樣可以減少其計算精度的損失。中心化的模型如下：

(19)

Xi′=Xi-ΔX,Yi′=Yi-ΔY

(20)

4.2 權的選取

4.3 精度評定

高程擬合的精度評定是通過內符合精度和外符合精度體現的。

內符合精度μ

(21)

式中n為參與擬合計算的已知點的殘差V的個數。

外符合精度M

(22)

式中V為檢核點的高程異常與擬合高程異常之差，n為檢核點的個數。

外符合精度能客觀地反映擬合的效果。當所選的已知數據點剛好位于所選模型附近時，內符合精度很高，它并不代表未知點有同樣的擬合精度。因此進行精度評定時要把內外符合精度權衡比較。

5 數據實驗

某高山峽谷區水電規劃測繪布設的GPS控制網見圖2，一共30個GPS點。平均邊長4.1km，測區平均海拔2 650m。平面等級為D級，高程按四等三角高程聯測。

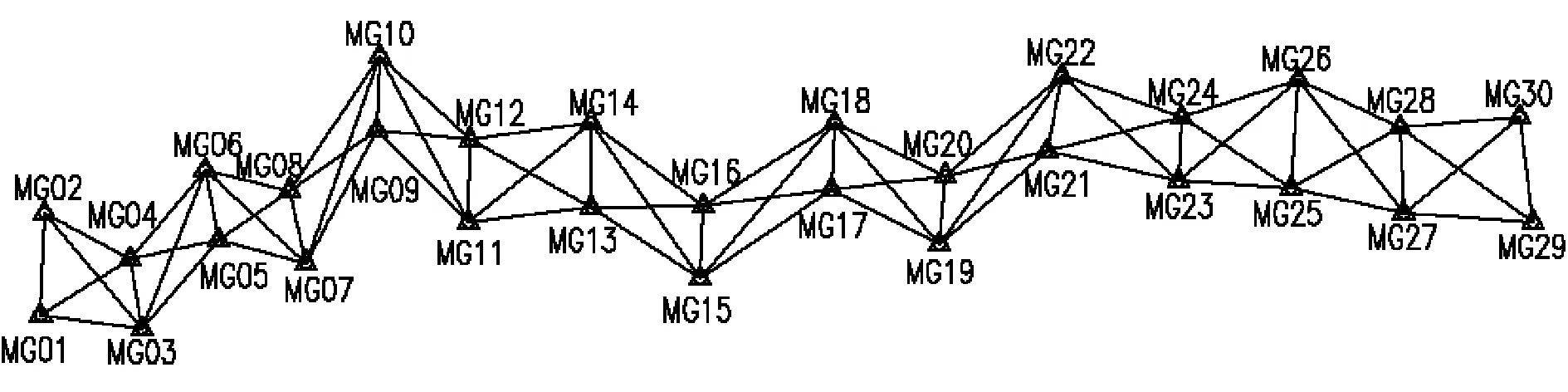
圖2 GPS網形示意

下面我們用以下四種方案進行高程擬合，設觀測值都為等權觀測。

方案一：用其中的6個點，以點的北京坐標為參數用二次六項式直接擬合高程異常；

方案二：先用EGM96擬合高程異常中的長波部分，求差后再用其中的6個點用一次三項式擬合高程異常之差；

方案三：同方案二，只是將已知點的個數增加為9個；

方案四：先用EGM96擬合高程異常中的長波部分，求差后再用其中的9個點用二次六項式擬合高程異常之差。四種擬合方法的精度結果見表1：

表1 四種擬合方法精度比較 m

從表1可以看出：基于地球重力場模型的GPS高程擬合法采用合適的數學模型精度高于單純的多項式擬合法，該方法隨著已知點的增多精度會提高，但當已知點增加到一定數量后精度不會進一步提高，這是由于多項式的runge現象造成的；方案二、三外符合精度相當，但方案二已知點個數只占所有點數的20%，因此方案二比方案三更為實用(見表2)。

表2 方案二高程差異量統計

從表2可看出，方案二達到五等水準精度，除個別點超限外基本達到四等水準的精度。而且超限的點均位于已知點附近，這是由于多項式擬合的振蕩現象引起的，可以通過分段擬合或適當增加已知點的個數從而達到擬合結果精度達到四等水準的要求。

6 結 語

基于地球重力場模型的GPS高程擬合法已逐漸成為研究局部精化大地水準面的重要手段。如果地球重力場模型的精度越高、使用的擬合函數得當、高程聯測點布設合理擬合精度將會越高，可以滿足高山峽谷區四等水準精度。對于不同形狀的GPS網，擬合高程的方法也不同，需經過計算和分析選定擬合函數。

參考文獻：

[1] 徐紹銓,等.GPS測量原理及應用[M].武漢大學出版社.2005(2).

[2] 武漢測繪科技大學測量平差教研室編.測量平差基礎[M].測繪出版社.1996(5).

[3] 陸彩萍,等.顧及EGM96模型的GPS水準高程擬合[J].測繪工程,2002(3).

[4] 程衛興.GPS水準方法比較分析.測繪與空間地理信息[J].2005.

[5] 喬仰文,等.GPS高程擬合的幾種常用方法[J].東北測繪，1999(2).