航空公司服務質量評價
——基于非可加直覺模糊VIKOR方法

章 玲，張露平，周 鵬

（1.南京航空航天大學經濟與管理學院，江蘇 南京 210016； 2.南京航空航天大學能源軟科學研究中心，江蘇 南京 210016）

航空公司服務質量評價
——基于非可加直覺模糊VIKOR方法

章 玲1，2，張露平1，2，周 鵬1，2

（1.南京航空航天大學經濟與管理學院，江蘇 南京 210016； 2.南京航空航天大學能源軟科學研究中心，江蘇 南京 210016）

文章針對航空公司服務質量評價過程存在的不確定性和非可加性，在三角直覺模糊數、模糊測度和VIKOR等理論的基礎上構建非可加直覺模糊VIKO多準則評價方法，從“保證性”、“服務人員”、“有形性”、“可靠性”四個方面建立評價指標體系。基于此對六家航空公司的服務質量的進行了評價。被評價航空公司的服務質量由高到低大致可以分為三等級：第一等級為中國國際航空公司和四川航空公司；第二等級為海南航空公司；第三等級為東方航空公司、南方航空公司和深圳航空公司。另外，與可加多準則評價方法對比研究的結果顯示指標間的非可加性對評價結果有較明顯的影響。

航空公司；三角直覺模糊數；模糊測度；服務質量

一、引言

隨著生活水平不斷提高，旅客對航空運輸服務質量有著更全方位的要求，既包括飛機客艙設備、地面服務環境等硬件要求，也包括對服務人員態度、服務的方便性等軟件方面的要求。如何改善航空公司的服務質量以增強對旅客的吸引力，從而提升航空公司的競爭力，已經成為國內航空公司迫切需要解決的一個關鍵問題。改善服務質量的前提是了解自身服務質量的情況，這就需要建立有效的評價指標體系和評價模型測評航空公司服務質量，為航空公司改善服務質量提供相關的決策支持。

目前，國內外學者對航空公司服務質量評價指標體系和評價模型都做了相當多的研究。例如Tsaur，Chang，Yen從有形性、可靠性、響應性、保證性以及移情性五個方面構建航空公司服務質量評價指標體系，集成AHP、語言變量、模糊集理論和TOPSIS評價航空公司服務質量[1]。Chang，Yeh從機上舒適性、服務人員、可靠性、接受服務的方便性以及對非正常情況的處理能力五個方面構建了包含15個指標的評價指標體系，結合語言變量、模糊集理論，借用逼近理想解思想構建了航空公司服務質量模糊綜合評價模型[2]。Kuo認為三角區間模糊數能更好的描述旅客偏好特征，因此集成語言變量、三角區間模糊數、VIKOR、灰色關聯度分析構建了區間模糊多準則評價模型對臺灣航空公司服務質量進行評價[3]。另外，還有學者運用模糊有序加權平均法[4]，支配關系的粗糙集理論[5]和變一致性優勢關系粗糙集理論[6]評價航空公司服務質量。

然而，現有評價航空公司服務質量的文獻通常基于經典測度理論。該理論要求指標間的關系滿足完備性、獨立性等條件。但現實中很難找到一組既相互獨立又全面的評價指標。現有文獻普遍假設指標之間的關系是獨立、可加的。可是這種假設并不一定符合實際情況。例如航空公司服務質量評價中廣泛使用的SERVQAUL量表共有五個維度（見表1），根據其對維度的定義，可以看出各維度之間存在一定的非可加性。有形性與保證性兩者的作用都是給予旅客信任和安全感；可靠性與移情性維度都包含了以正確的服務方式的含義。因此，SERVQUAL量表中維度之間并不獨立。而張新安、田澎[7]也指出SERVQUAL量表不同維度下的指標具有較強的相關性。

表1 SERVQUAL量表維度[1，8]

另外，安濤等的研究[9]評價航空公司服務質量時均使用了“能夠信守服務承諾”、“能夠給予旅客信任”以及“能夠專業的回答旅客問題”三個指標。從其表達的含義可以看出這三個指標并不獨立，因為如果能夠信守其承諾本身就能夠增加旅客對航空公司的信任。同樣，能夠專業的回答旅客問題也能增加旅客對航空公司的信任。又如PAKDIL等人[10，11]的相關研究均使用“了解旅客個人需求”、“興趣特征和針對旅客個人情況給予特殊照顧”兩個指標，不難想象了解旅客的個人需求是給予特別幫助的前提。類似這樣的情況普遍存在于現有文獻中。

為了克服以上問題，文章引入模糊測度理論。該理論是用較弱的單調性代替了概率測度的可加性[12]。目前，模糊測度理論被廣泛應用于考慮指標偏好間存在非可加性時的多準則評價建模中。Marichal論證了系統中存在的非可加性均可用模糊測度進行度量[14]。在主觀多準則評價中，模糊測度可以被認為是傳統權重概念的推廣。運用模糊測度構建航空航空公司服務質量評價模型時，不僅需要單個指標的權重，同時也會考慮指標冪集的權重。因此，模糊測度理論能很好的考慮指標間的非可加性，較傳統的可加理論也更符合實際情況。此外，考慮到在獲取數據的過程中，由于是讓航空旅客根據自己的親身經歷評價航空公司服務質量，可能存在一定的不確定模糊性和猶豫性。三角直覺模糊數能夠較好的刻畫以上特性[15]。基于以上原因，文章結合三角直覺模糊數、模糊測度和VIKOR方法構建非可加直覺模糊VIKOR方法評價航空公司服務質量。

二、基本概念

1.三角直覺模糊數

定義1[16]：三角直覺模糊數為定義在實數集R上的特殊的直覺模糊集，其隸屬度μa(x)和非隸屬度函數υa(x)分別為：

其中wa~，ua~分別為最大隸屬度和最小非隸屬度，且滿足：0≤wa~≤1，0≤ua~≤1，和0≤wa~+ua~≤1。令πa~=1-μa~(x)-υa~(x)，則πa~是三角直覺模糊數a~的直覺模糊指數，反映的是x屬于a~的猶豫程度。

2.λ模糊測度

對于任一多準則評價問題，C={C1，C2，…，Cn}為評價指標集。定義在指標集C上的離散模糊測度為一單調集函數μ∶2C→[0，1]，且滿足μ(?)=0，μ(C)=0。直接運用離散模糊測度對多準則評價問題建模時需要決策者確定2n-2模糊測度值。這給實際建模造成了一定的困難。因此不少學者在模糊測度的基礎上增加約束條件，定義新的模糊測度。λ模糊測度就是其中之一。

定義2[12]：定義在指標集C上的λ模糊測度為一單調集函數gλ∶2C→[0，1]，且滿足如下條件：

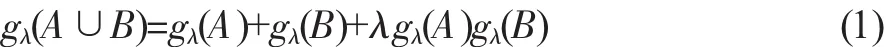
其中λ∈(1，-∞)，A，B∈2C且A∩B=?。從條件(1)可以看出，當λ=0時，說明指標間具有可加性；當λ≠0時，說明指標間存在交互作用。而當λ＞0時，說明指標間存在協同互補作用；相反，說明指標間存在冗余作用。

為了求解各個指標及其冪集的λ模糊測度gλ(S)，本文引入了基于λ模糊測度的Shapley值。

定義3[17]：若gλ為定義在C上的λ模糊測度，對于任意的S∈2C，其Shapley值?(gλCi)為：

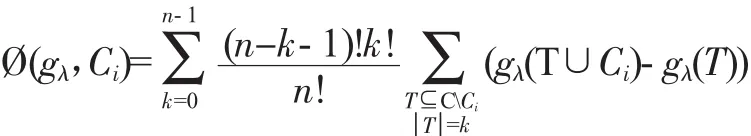
Shapley值?(gλ，Ci)可以解釋為指標Ci的邊際貢獻加權平均值，即單個指標Ci的權重。因此，可以通過常規主客觀賦權法得到?(gλ，Ci)值。

三、非可加直覺模糊VIKOR方法

假設C={C1，C2，…，Cn}為評價指標集，A={A1，A2，…，Am}為方案集，有P個決策者。結合李克特量表評價航空公司服務質量，評價值與三角直覺模糊數的對應關系如表2和表3所示。為決策者k(k=1，2，…，P)對方案Ai在指標Cj下的三角模糊數評價值。則Ai在指標Cj下的綜合評價f~ij為：

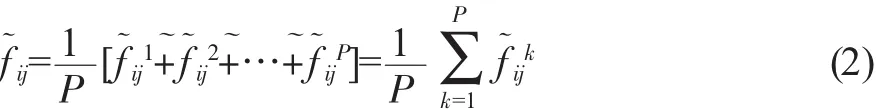
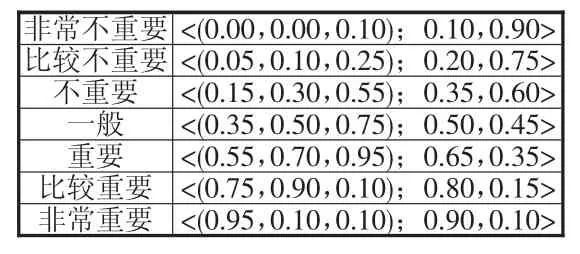
表2 語言變量與指標權重對應表

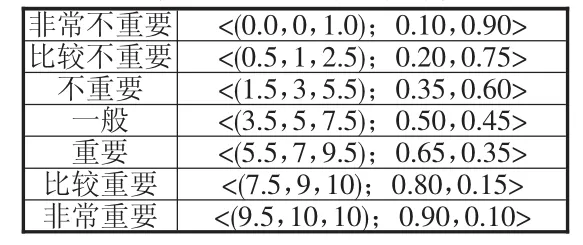
表3 語言變量與指標評價值對應表

運用非可加VIKOR方法評價航空公司服務質量的關鍵是求解各個指標及其冪集的λ模糊測度，即各個指標及其冪集的權重。由于各指標的?(gλk，Ci)值可以通過常規主客觀賦權法得到。因此，結合λ模糊測度的Shapley值?(gλk，Ci)和Marichal熵[19]對λ模糊測度建模，可以求解各指標及其冪集的λ模糊測度和λ值，模型如(3)所示。

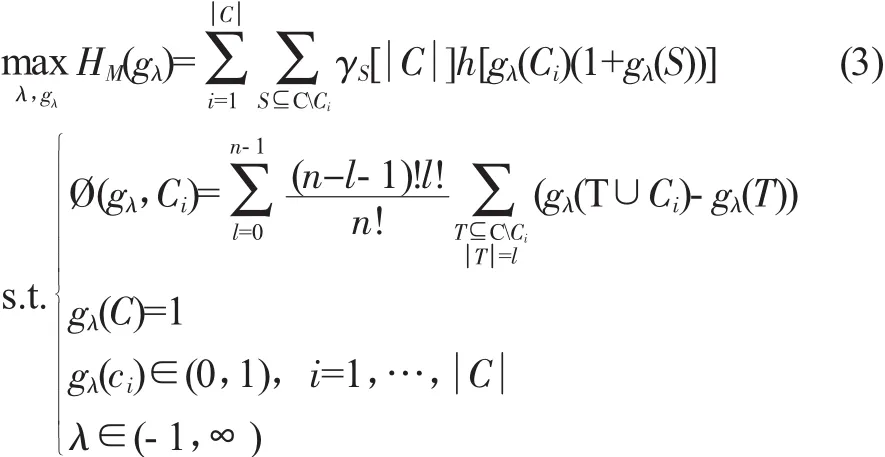
其中：

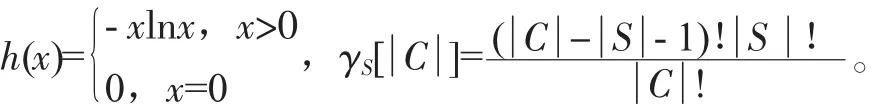
當各個指標的λ模糊測度值確定之后，可以根據條件按需計算各個指標冪集的λ模糊測度值gλ(S)(S∈C)。

在獲取各個指標及其冪集的λ模糊測度值后，在標準化三角模糊決策矩陣的基礎上，首先按照如下公式確定正理想解和負理想解：

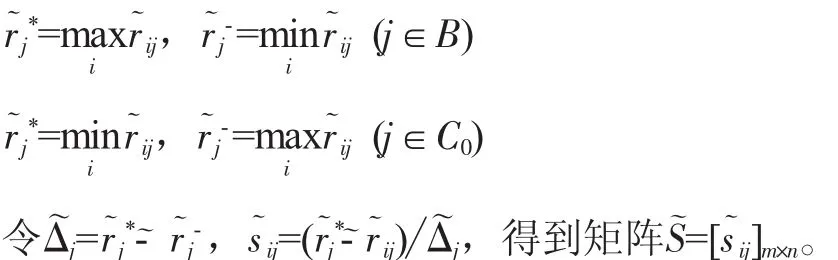
非可加直覺模糊VIKOR方法運用各指標的λ模糊測度作為其權重，不僅考慮了單個指標項Ci(i=1，2，…，n)的權重gλ(Ci)，而且需要綜合考慮包含指標Ci的所有子集S(S?C)的權重gλ(S)。正是λ模糊測度的這一特性使得該方法能夠捕捉到指標間的非可加性。因此，計算矩陣的綜合值時，傳統的基于可加的集結算子失效。

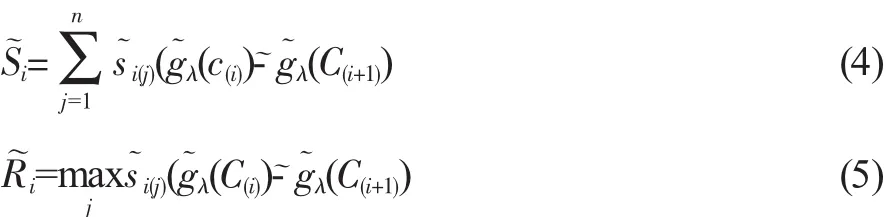
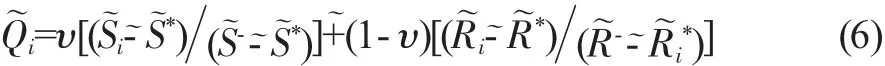
方案集的折衷方案A(1)是值最小的方案，并且滿足如下條件：

條件2：A(1)是Si、Ri值最小方案。

如果上述條件中有一個不滿足，則根據如下條件選擇折衷方案：

①如果條件2不滿足，方案A(1)，A(2)均為折衷解；

②如果條件1不滿足，方案A(1)，A(2)，…，A(r)為折衷解，其中A(r)滿足Q(A(r))-Q(A(1))≥1(m-1)。

綜上所述，非可加直覺模糊VIKOR評價方法的求解步驟如下：

步驟1：分析影響評價對象的因素，根據指標構建原則，建立評價對象的指標，并設計問卷，對評價對象進行問卷調查，收集相關數據；

步驟2：確定評價評價對象的語言變量以及其與三角直覺模糊數的對應關系，采用三角直覺模糊數量化收集到的相關數據，以便得到初始三角直覺模糊數決策矩陣；

步驟3：標準化初始三角直覺模糊決策矩陣；

步驟4：運用模型(3)計算指標及其冪集的λ模糊測度和λ值；

步驟5：根據標準化后的三角直覺模糊決策矩陣確定正負理想解；

步驟7：計算Qi值，根據、以及值按照確定折衷方案規則選擇最優方案或者是折衷方案。

四、基于非可加模糊VIKOR方法的航空公司服務質量評價

1.評價指標構建

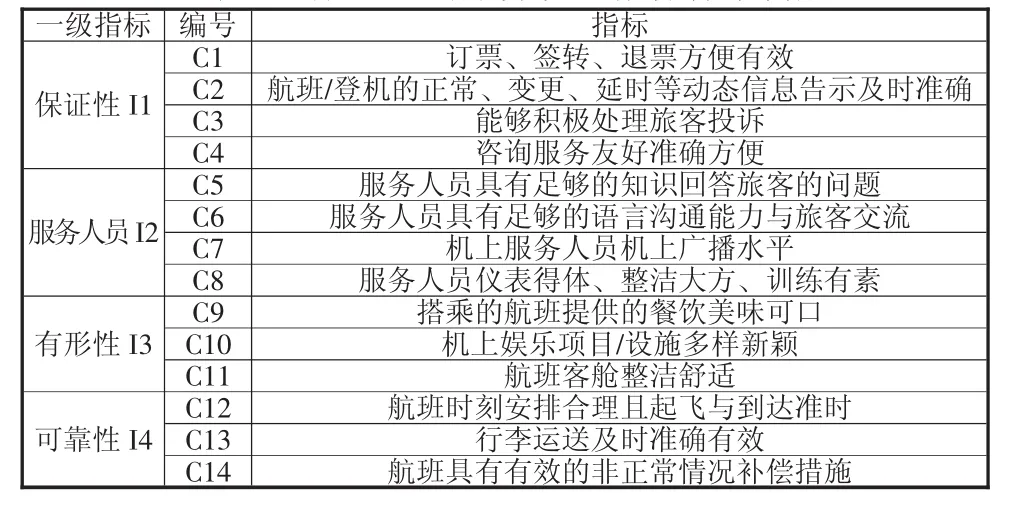
表4 航空公司服務質量指標體系構成

文章首先通過文獻分析，搜集和整理國內外已有航空公司服務質量評價指標資料，構建初始評價指標。然后通過關鍵因素調查法，經過實際樣本調查，對初始評價指標要素進行重要性判斷，最后從“保證性”、“服務人員”、“有形性”、“可靠性”四個方面建立了包含14項指標的評價體系（見表4）。之后于2013年8月下旬至9月中旬，通過網上問卷、電子郵件以及實地調研的方式隨機抽取搭乘或者是近期搭乘過航班的旅客進行滿意度和指標重要程度的問卷調查。為了保證問卷數據的可信性和精確性，文章選擇問卷數超過30份的航空公司作為評價對象。問卷數超過30份的航空公司有中國國際航空公司(A1)、中國東方航空公司(A2)、中國南方航空公司(A3)、海南航空公司(A4)、四川航空公司(A5)、深圳航空公司(A6)。對滿意度調查問卷運用公式(2)計算得到初始評價矩陣，標準化初始評價矩陣可以得到如表5所示的標準化評價矩陣。

2.指標Shapley值的確定

根據前文對Shapley值的定義，文章采用混合賦權法確定各個指標的Shapley值。首先確定各個指標的混合權重。各個指標的主觀權重為：

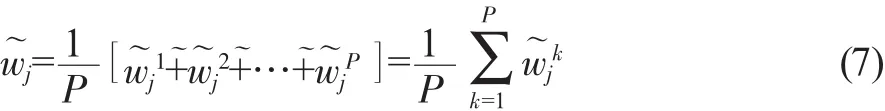
綜合主客觀權重，航空公司服務質量評價各個指標的權重為：

根據公式(7)、(8)、(9)可以得到航空公司服務質量評價指標的混合權重（見表6）。

以各指標權重標準化后的值作為指標Shapley值，標準化方法如下：以每一級指標對應的二級指標的權重和作為各個一級指標的Shapley值，以此為基數，對各個指的權重標準化得到最終的各個指標的Shapley值。以及一級指標保證性及其對應的二級指標為例來說明計算Shapley值的過程：C1、C2、C3和C4的權重分別為0.101、 0.081、0.113和0.066，則保證性的Shapley值為該4項指標的Shapley值和，即：0.362，以此數為基數，對以上4項指標的權重進行標準化得到：0.280，0.22 4，0.313，0.182。同理可以計算其他一級指標及其對應的二級指標的Shapley值，見表7。

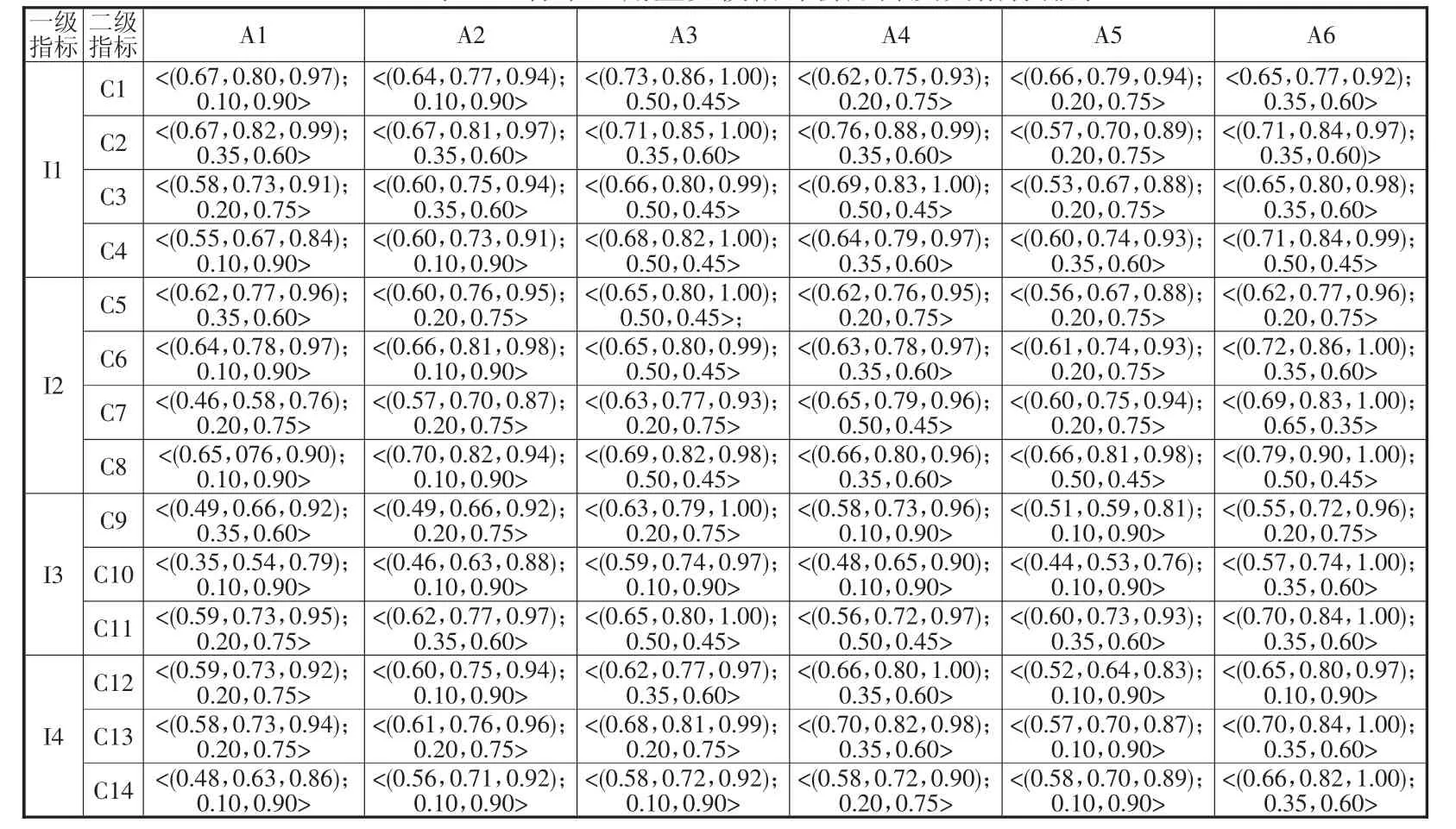
表5 標準三角直覺模糊評價矩陣及其指標排序

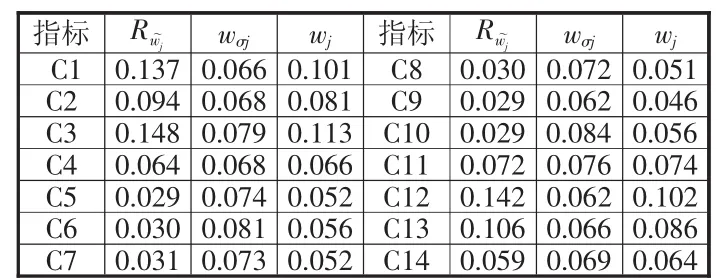
表6 指標權重值

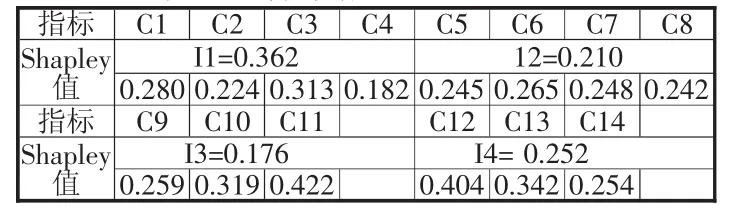
表7 各個指標Shapley值

3.指標λ模糊測度的確定

隨后，根據模型(3)，計算得到各級指標的λ模糊測度值及λ值，其結果見表8。表8顯示：二級指標C1、C2、C13、C14的λ值為負值。由此，C1、C2、C13、C14指標間存在一定程度的冗余關系。其他維度中的二級指標對應的λ值均為較大的正值，說明對應指標間均表現出明顯的互補關系。一級指標I1、I2、I3、I4的 λ值為 20.9283，這說明一級指標之間也具有比較明顯的互補關系。

4.評價結果及分析

在得到各指標的λ模糊測度值之后，可以根據公式(4)、(5)、(6)分別計算、、值，具體見表9。

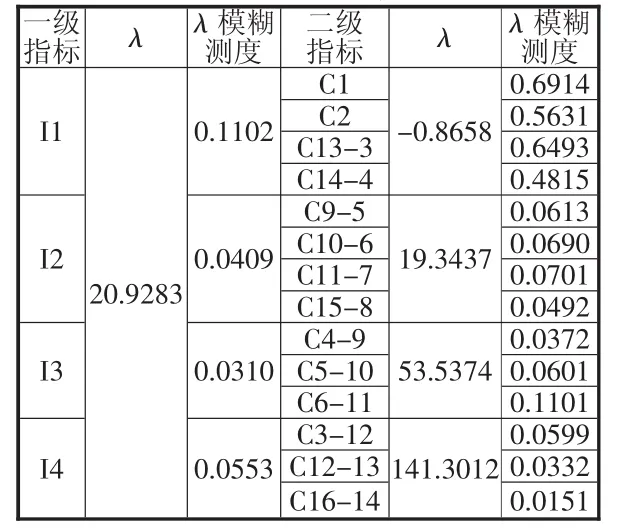
表8 各個指標λ模糊測度及其對應的λ值

根據文章第三部分的非可加直覺模糊VIKOR方法的決策規則，由Qi值可以知道各個航空公司服務質量績效情況。表7顯示，當υ=1或者υ=0.5時，各個航空公司服務質量績效排序結果為：A1＞A5＞A4＞A2＞A3＞A6；當υ=0時，各個航空公司服務質量績效排序結果為：A5＞A1＞A4＞A2＞A3＞A6。實際上，通過試探性分析發現，只要υ＞0.2時，Qi值排序結果均為第一種情況；當υ≤0.2時，排序情況均為第二種情況。但是不管υ值如何，我們發現A2、A3、A6航空公司的排名均靠后，說明不管是從群決策或者是個體決策角度來說，旅客感知到的A2、A3、A6航空公司的服務質量劣于其他三家航空公司；A4航空公司的服務質量不管是在第一種情況還是第二種情況，其排名均無變化。A1，A5航空公司服務質量在兩種情況中的排名會互換位置，第一種情況中，A1優于A5；在第二種情況中，A5優于A1，但不管是那種情況，A1、A5航空公司提供的服務質量均優于其他的航空公司。從整體來說，A1、A5、A4航空公司的服務優于A2、 A3、A6。另外，當υ=0時，表示以服務質量排名第一的航空公司為參考，其他航空公司自身的服務質量要達到其服務質量水平應該花費的精力。因此，相比較于A1、A4達到A5的服務質量水平，在各個指標上要比A1航空公司花費更多的精力，同時也說明，其服務質量劣于A4航空公司。同理，也可以比較其他的航空公司服務質量狀況。

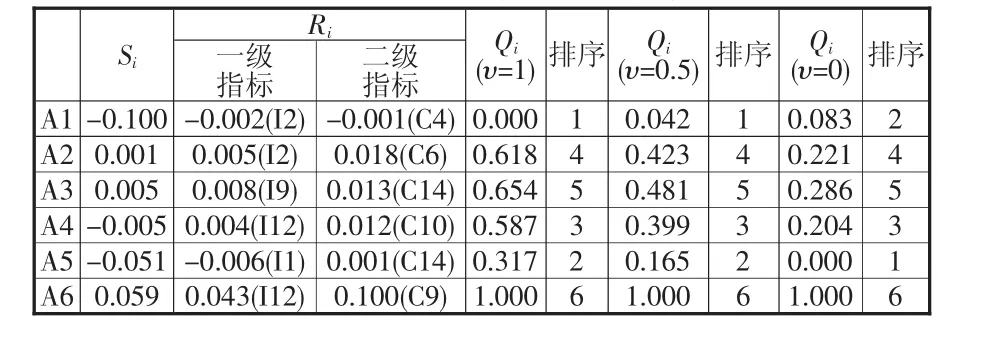
表9 航空公司服務質量評價結果

5.對比分析

下面將基于非可加直覺模糊VIKOR多準則評價方法（記為IFL-VIKOR）的航空公司服務質量評價結果與直覺模糊算術加權平均法（記為IF-WAM），直覺模糊VIKOR評價方法（記為IF-VIKOR）以及基于Choquet積分的評價方法（記為IF-Choquet）的評價結果進行橫向對比。IF-WAM和IF-Choquet計算步驟參考附錄；IF-VIKOR計算步驟參考DEVIK的研究[21]。 根據相應步驟，評價結果分別為：

對比結果如圖1所示。

從以上結果可以看出，不考慮指標偏好間的非可加性的IF-WAM評價結果與考慮了指標偏好間的非可加性的IF-Choquet評價方法的結果并不一樣；同樣，不考慮指標偏好間的IF-VIKOR方法評價結果與考慮了指標偏好間的非可加性的IFL-VIKOR方法評價結果也不盡相同。由此可以看出，指標偏好的非可加性明顯影響最終評價結果，基于非可加直覺模糊VIKOR多準則方法對航空公司服務質量評價研究可以使最終評價結果更加的科學，符合實際情況，有利于航空公司管理人員做出更為合理的決策。

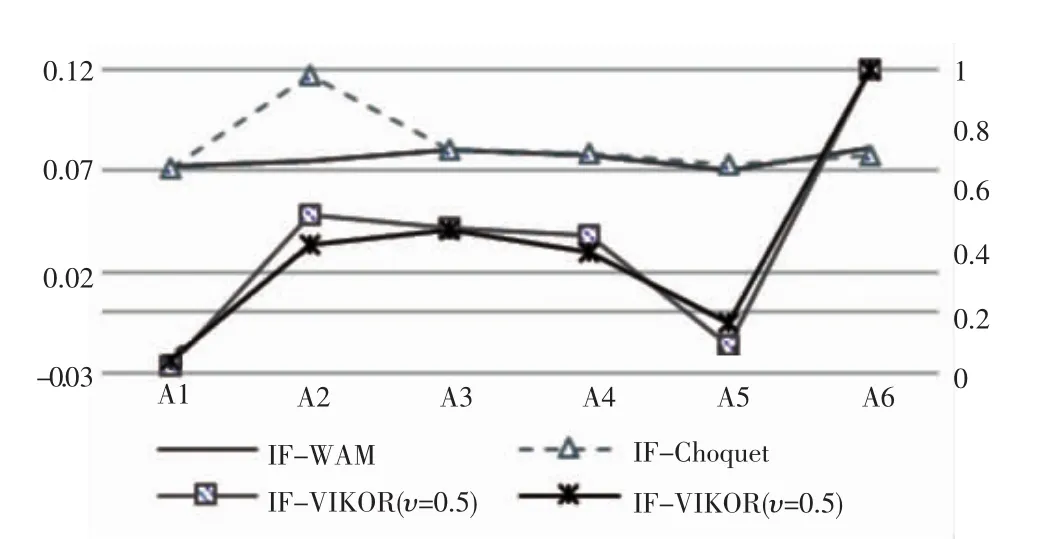
圖1 不同評價方法評價結果對比

附錄——基于三角直覺模糊評價矩陣的算術加權平均法計算步驟如下：

②運用算術加權平均集結算子M(x)=R×W計算航空公司服務質量綜合績效值。

③根據M值對航空公司服務質量進行排序擇優。

基于三角直覺模糊評價矩陣的Choquet積分評價方法計算步驟如下：

②以W值作為Shapley值，輸入模型(3)，計算各個指標的λ模糊測度值及其λ值。

五、結論

服務質量對于航空公司提升競爭力起著關鍵性的作用。為了給航空公司改善其服務子質量提供決策支持，需要對航空公司的服務質量進行測評。雖然目前已有較多文獻評價航空公司服務質量，但是普遍假設評價指標間的關系是獨立的，基于可加的多準則方法評價之。然而，現實中很難找到一組完全獨立的評價指標體系。這使得已有文獻的評價方法具有一定的局限性。另外，在獲取數據的過程中，由于是讓航空旅客根據自己的親身經歷評價航空公司服務質量，可能存在一定的不確定模糊性和猶豫性。基于以上原因，本文結合三角直覺模糊數、λ模糊測度和VIKOR等理論，構建了非可加直覺模糊VIKOR多準則評價方法。指標體系方面，根據文獻分析法和關鍵因素調查法，本文分別從“保證性”、“服務人員”、“有形性”、“可靠性”四個方面建立了包含14項指標的評價指標體系。基于以上模型和評價指標，本文對六家航空公司的服務質量進行了評價。評價結果顯示：指標間具有明顯的非可加性，特別是“服務人員”、“有形性”、“可靠性”中的指標項之間；被評價航空公司的服務質量可以大致分為三等級：第一等級包含A1中國國際航空公司、A5四川航空公司；第二等級為A4海南航空公司；第三等級為A2東方航空公司、A3南方航空公司、A6深圳航空公司。另外，與可加多準則評價方法對比研究顯示指標間的非可加性對評價結果有較明顯的影響；與其他多準則評價方法對比研究顯示指標間的非可加性對評價結果有較明顯的影響。

[1]Tsaur S-H，Chang T-Y，YEN C-H.The evaluation of airline service quality by fuzzy MCDM [J].Tourism Manage ment，2002，23(2)：107-15.

[2]CHANG Y-H，YEH C-H.A survey analysis of service quality for domestic airlines[J].European Journal of Operational Research，2002，139(1)：166-77.

[3]KUO M-S.A novel interval-valued fuzzy MCDM method for improving airlines'service quality in Chinese cross-strait airlines[J].Transportation Research Part E：Logistic and Transportation Review，2011，47(6)：1177-93.

[4]CHENG C-H，CHANG J-R，HOT-H，et al.Evaluating the A-irline Service Quality by Fuzzy OWA Operators [M].TORRA V，Narukawa Y，Miyamoto S.Modeling Decisions for Artificial Intelligence[J].Springer Berlin Heidelberg，2005:77-88.

[5]LIOU J J H，YEN L，TZENG G-H.Using decision rules to achieve mass customization of airline services[J].European Journal of Operational Research，2010，205(3)：680-6.

[6]LIOU J J H.Variable Consistency Dominance-based Rough Set Approach to formulate airline service strategies [J]. Applied Soft Computing，2011，11(5)：4011-20.

[7]張新安，田澎.應用SERVQUAL標尺的若干問題及改進 [J].系統工程理論與實踐，2006，6：41-8.

[8]Parasuraman A，Zeithaml V A，Berry L L.SERV-QUAL：A M-ultiple-Item Scale for Measuring Consumer Perceptions of Service Quality[J].Journal of Retailing，1988，64(1)：12-40.

[9]Erdil S T，Yldz O.Measuring service quality and a comparative analysis in the passenger carriage of airline industry[J]. Procedia-Social and Behavioral Sciences，2011，24(0)：1232-42.

[10]Pakdil F，AYD1N ?.Expectations and perceptions in airline services：An analysis using weighted SERVQUAL scores[J]. Journal of Air Transport Management，2007，13(4)：229-37.

[11]Chou C-C，Liu L-J，Huang S-F，et al.An evaluation of airline service quality using the fuzzy weighted SERVQUAL method[J].Applied Soft Computing，2011，11(2)：2117-28.

[12]Sugeno M.Theory of fuzzy integrals and its applications[D]. Tokyo Institure of Technology，1974.

[13]Grabisch M，Labreuche C.A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid [J].4OR，2008，6(1)：1-44.

[14]Marichal J L.An axiomatic approach of the discrete Choquet integral as a tool to aggregate interacting criteria[J]. Fuzzy Systems，IEEE Transactions on，2000，8(6)：800-7.

[15]XU Z，CAI X.Intuitionistic Fuzzy Information Aggregation：Theory and Applications[M].Springer London，Limited，2012.

[16]SHU M-H，CHENG C-H，CHANG J-R.Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly [J].Microelectronics Reliability，2006，46(12)：2139-48.

[17]章玲，周德群.λ模糊測度及其M?bius變換和關聯系數間關系的推導 [J].山東大學學報（理學版），2007，07：33-7.

[18]LI D-F.A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems[J]. Computers&Mathematics with Applications，2010，60(6)：1557 -70.

[19]Marichal J-L.Entropy of discrete Choquet capacities [J]. European Journal of Operational Research，2002，137(3)：612-24.

[20]BY..YY..K ZKAN G.Applying a Choquet Integral Based Decision Making Approach to Evaluate Agile Supply Chain Strategies[M].Computational Intelligence in Complex Decision Systems，Atlantis Press，2010：373-86.

[21]DEVI K.Extension of VIKOR method in intuitionistic fuzzy environment for robot selection[J].Expert Systems with Applications，2011，38(11)：14163-8.

（責任編輯：FZF）

Evaluating Airline Service Quality——Anon-additive VIKOR Methods in Intuitionistic Fuzzy Settings

ZHANG Ling1，2，ZHANG Lu-ping1，2，ZHOU Peng1，2
（1.College of Economics and Management，Nanjing University of Aeronautics and Astronautics，Nanjing Jiangsu 210016，China； 2.Research Centre for Soft Energy Science，Nanjing University of Aeronautics and Astronautics，Nanjing Jiangsu 210016，China）

In order to seize the characteristics of non-additive and uncertainty in the evaluation procedure，this paper construct a non-additive VIKOR method in intuitionistic fuzzy settings based on the integration of VIKOR， fuzzy measure and intuitionistic fuzzy theory.This paper also established evaluation criteria for airline service quality with four dimensions："Reliability"，"Employees'service"，"Tangibles"and"Assurance".Six airline's services are assessed with the help of the criteria and the method.The results show that the service performance of the six airlines could be divided into three levels:the first level includes airline A1 and A5，second includes A4.The remain belong to third level.Comparative studies are also carried out which results suggested that the property of non-additive between criteria obviously impact on the results.

Airline；VIKOR；Fuzzy measure；Quality of service

F562.3

A

1004-292X（2014）04-0008-07

2013-12-01

國家自然科學基金資助項目（71101070，71273005）。

章 玲（1979-），女，安徽肥東人，博士，副教授，主要從事復雜系統評價與決策研究；

周 鵬（1978-），男，山東諸城人，博士，教授，主要從事能源效率與碳排放政策研究。