限制性哈密頓系統中局部坐標的選取對數值計算的影響

李江丹，張素英

（1.太原師范學院 物理系，太原 030012；2.山西大學 理論物理研究所，太原 030006）

一、局部坐標法

我們考慮拉格朗日系統。令r∈Rn為系統的位置坐標，r˙為其速度。設系統的拉格朗日函數已經給定：L（r,r˙）=T-V，其中 T 是系統的動能，V 是系統的勢能。我們可以通過勒讓德變換得到系統的哈密頓函數，然后用哈密頓函數得到哈密頓正則方程。對一般的哈密頓系統人們已經發展了很多高效的數值計算方法，無疑辛算法［1-2］是其中的佼佼者。辛算法在長時的跟蹤計算上有傳統解微分方程的龍格-庫塔方法無法比擬的優勢。但是如果系統處在某種約束之下，人們除了辛方法外，還得加上約束條件。針對這種情況人們已經發展了很多約束辛算法來解決這個問題。如果給定系統的約束為完整約束，那么我們可以引入合適的局部坐標來研究限制流形上的運動方程，這種方法被稱為微分-幾何方法［3-5］。它可以把微分-代數系統轉變為一個流形上的微分方程。我們可以在這個流形上引入合適的局部坐標來求解運動方程。限制性代數方程可以定義一個光滑流形M。如果存在一個開區域可以覆蓋所有的可能運動區域，那么這個開區域可以用局部坐標參數，進而我可以得到該流形上的拉格朗日函數，用勒讓德變換可以得到系統在該流形上的的哈密頓函數：

約束解除后，我們就把原來限制性哈密頓系統的方程轉化為非限制哈密頓系統的方程，仍然可以使用通常的辛算法進行數值求解。顯然，哈密頓函數的形式取決于局部坐標的選取，我們將證明不同局部坐標系下的辛形式都是等價的。理論上不同局部坐標的等價性并不能帶來具體計算當中的精度相當，事實上在具體的數值計算當中卻表現為：在某些局部坐標下計算結果比較好，在另一些局部坐標下計算結果較差。

二、哈密頓系統辛格式的不變性

在使用辛算法求哈密頓方程的數值解時,我們希望系統的能量也是近似守恒,但是我們通過具體例子可以發現系統的能量的相對誤差不僅取決于算法的精度,還取決于我們選取的局部坐標。

三、局部坐標的選取

原哈密頓系統可以通過引入適當的局部坐標來進行數值求解,并且具有限制不變性。從理論上講,任何一種局部坐標都可以進行數值計算,因為所有的局部坐標都是等價的。但是我們并不能從實踐的角度給以說明。我們通過具體的數值計算的例子發現系統能量是否近似守恒很大程度上取決于選取的局部坐標。

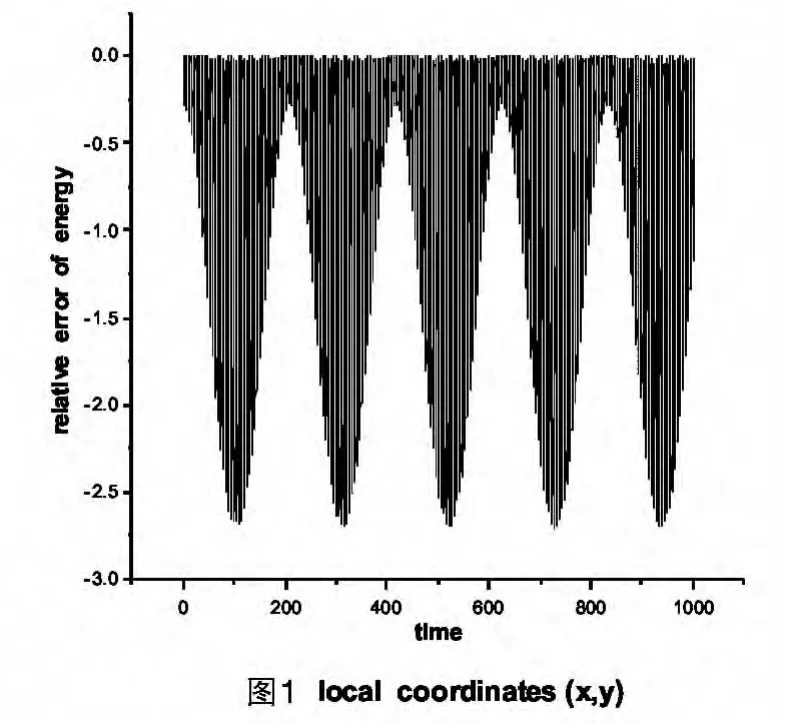
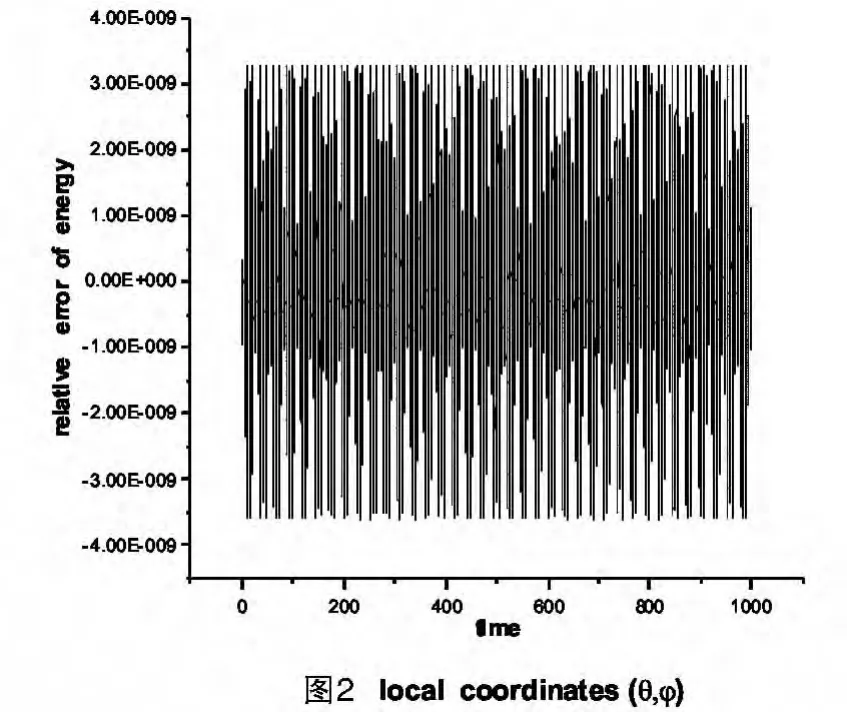
我們用這兩種局部坐標（x，y）和（θ，φ）來進行數值求解。可以使用2階和4階辛方法［1-3］，選取步長為h=0.01。如圖1和圖2所示,在時間間隔［0，1000］內研究能量的相對誤差，局部坐標（θ，φ）的能量相對誤差近似守恒，而局部坐標（x，y）的能量相對誤差就比較大。

四、結論

本文我們使用局部坐標法解決了限制性哈密頓系統的數值求解運動方程問題，通過具體的例子討論了局部坐標法的具體細節。在給出的案例中,用局部坐標（x，y）的能量相對誤差量級為100,如果用另一個局部坐標（θ，φ）能量的相對誤差量級為10-9。我們可以看到用局部坐標法求解限制性哈密頓系統時,選取合適的局部坐標是很重要的。在局部坐標下,系統能量是近似守恒的,但是在某些坐標下能量的相對誤差可能比較大。從本文案例的坐標選取來看,哈密頓函數表達式簡練的坐標在計算時的誤差要小。因為表達式簡練反應到計算程序里就是計算量較少，這樣就有效的的減少了誤差的累積，也就是提高了精度。但在上述案例中精度在量級上的差別是無法解釋的。對限制性哈密頓系統哪種局部坐標是最佳選擇尚沒完全解決。

［1］Zhang S.Y.，Deng Z.C.Geometric Tntegration Theory of Nonlinear Dynamical System and Its Application［M］.Xi’an：Northwestern PolytechnicalUniversity Press，2005.

［2］FengK.and QinM.Z.SymplecticGeometric Algorithms forHamiltonian Systems［M］.Hangzhou：ZhejiangScience and Technology Press,2003.

［3］Hairer E.and Wanner G.Solving Ordinary Differential Equations II［J］.Springer-Verlag,1991.

［4］Westenholz C.von.Differential Form in Mathematical Physics［J］.North Holland,1981.

［5］余揚政，馮承天.物理學中的幾何方法［M］.北京：高等教育出版社，1998.