獨立測角網極條件列立規律研究與應用

孫琴琴，崔 娜

（晉城職業技術學院，山西 晉城 048026）

一、前言

極條件方程是獨立測角網用條件平差法平差時需要列出的條件方程類型之一，列立極條件方程是獨立測角網條件平差法平差的一項重要內容，也是難點之一。該條件方程對比其它類型的條件方程，如圖形條件（內角和條件）方程和圓周條件（水平條件）方程，冗長、繁雜，不容易一眼看出。因此，如何在復雜的表象下尋求規律和利用規律成為高效準確列立極條件方程的關鍵。

二、獨立測角網極條件列立規律

圖1為一測角中點三角形，A、B為已知點，C、D為待求點，網中觀測了9個角度。該圖形必要觀測數為4，多余觀測數為5，應列5個條件方程，這5個條件方程分別由3個圖形條件（內角和條件）方程、1個圓周條件（水平條件）方程和1個極條件方程組成。3個圖形條件（內角和條件）方程和1個圓周條件（水平條件）方程很容易列出,這里不再贅述。極條件是一種邊長條件，以中心D點為頂點，有三條邊:DA、DB和DC。從其中任意一條邊開始依次推算其它各邊的長度,最后又回到起始邊,得出推算起始邊長度,而推算起始邊長度理應等于起始邊長度，即這兩個長度構成幾何邊長約束條件。如圖1所示，以DA邊為起算邊,應用正弦定理，依次推算DB、DC，最后轉了一圈,推算出DA，推算起始邊長度理應等于起始邊長度，整理后得：

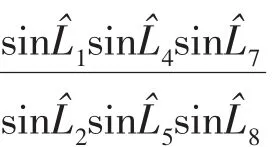
將上述非線性形式的極條件平差值方程化為線性形式，通常有兩種方法［1，2］：用臺勞公式展開取至一次項或先取對數，再按臺勞公式展開成線性形式。兩種方法的線性化結果一致：

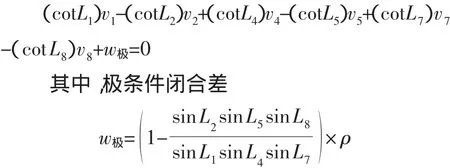
ρ為1弧度所對應的秒數，即206265″。

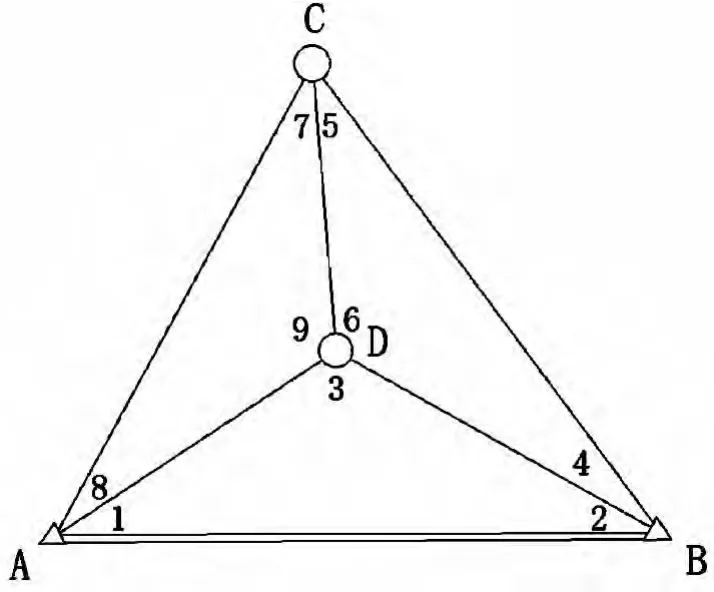
圖1 中點三角形

通過對上述獨立測角網列立極條件的過程和極條件形式進行分析、總結，我們可得出以下明顯規律：

（一）平差值極條件方程需要線性化

條件平差中，法方程系數需根據線性形式條件方程的系數和權組成，所以非線性形式的極條件方程需轉化成線性形式。

（二）以中點為極的邊，無論從哪條邊開始推算，得出的極條件方程都一致

如圖1所示，無論以DA、DB或DC哪條邊為起算邊，依次推算轉一圈，得出的極條件方程一致。

（三）極條件方程式中，改正數的系數為相應觀測值的余切

如圖1所示，極條件方程的系數分別為相應觀測值的余切cot L1、cot L2等。

（四）平差值極條件方程中，出現在分子位置的觀測值，在極條件方程式中符號為“＋”，出現在分母位置的觀測值，在極條件方程式中符號為“－”

如圖1所示，平差值極條件方程中，出現在分子位置的觀測值，如 L1、L4、L7，在極條件方程式中符號為“＋”，出現在分母位置的觀測值，如，L2、L5、L8在極條件方程式中符號為“－”。

（五）在極條件閉合差w極的表達式中，平差值條件方差中對應的分子分母要交換位置

如圖1所示，平差值極條件方程中，出現在分子位置的觀測值，如 L1、L4、L7，在極條件閉合差中在分母位置；出現在分母位置的觀測值，如，L2、L5、L8在極條件閉合差表達式中處在分母位置。

以上規律可整理為口訣：“極條件要線性化，審核需要轉個圈，系數為其余切值，只出現相關角度值，符號正負相交替，相似位置符號同。常數項，閉合差，分子分母換位置。”

三、算例

例1：如圖1所示，9個同精度獨立觀測值分別為［3］：

（根據規律，可直接列出線性形式的極條件方程，用推算轉圈的過程規律審核即可。）

該極條件方程中，改正數vi（i=1，2…，9）前的系數為其相應觀測值的余切值，符號“＋”、“－”交替，且只出現和正弦定理推算相關的角度值，如L1、L2、L4、L5、L7、L8這 6 個角度。以 D 為頂點，相似位置符號相同，如 L1、L4、L7位置（推算方向前進邊對應角度）對應符號均為“＋”，L2、L5、L8位置（推算方向后視邊對應角度）對應符號均為“－”。閉合差表達式中，相對平差值方程表達式，分子分母換位置，符合規律口訣所述。

根據已知觀測值，得：

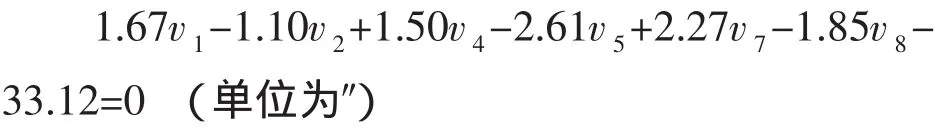
例2：寫出如圖2所示中點五邊形P-ABCDE極條件方程式。

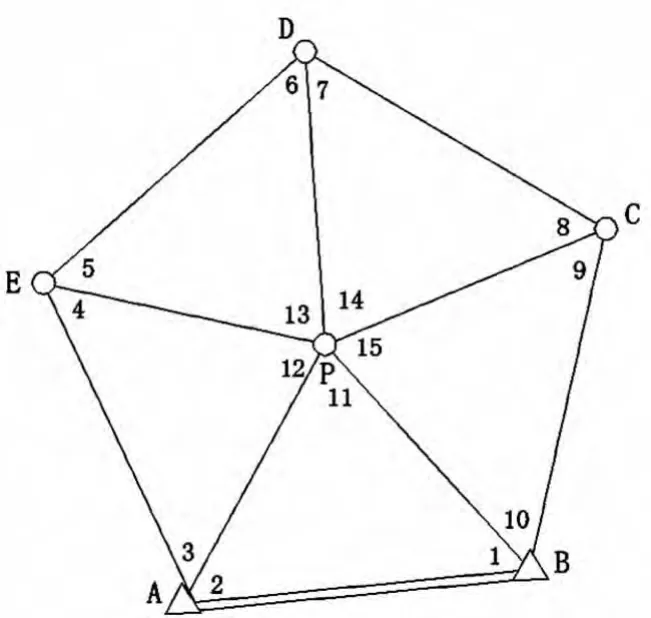
圖2 中點五邊形

解：如圖所示中點五邊形P-ABCDE，以P為極，PB為起算邊，分別按△PAB、△PEA、△PDE、△PCD、△PBC順序轉個圈，推算出PB邊，推算出的PB邊應等于PB,經整理，得平差值極條件方程式為：

該極條件方程中，改正數vi（i=1，2…，9）前的系數為其相應觀測值的余切值，符號“＋”、“－”交替，以P為頂點，相似位置符號相同，如 L1、L3、L5、L7、L9位置（推算方向前進邊對應角度）對應符號均為“＋”，L2、L4、L6、L8、L10位置（推算方向后視邊對應角度）對應符號均為“－”。閉合差表達式中，相對平差值方程表達式，分子分母換位置，符合規律口訣所述。

例3：寫出圖3所示大地四邊形的極條件方程式。

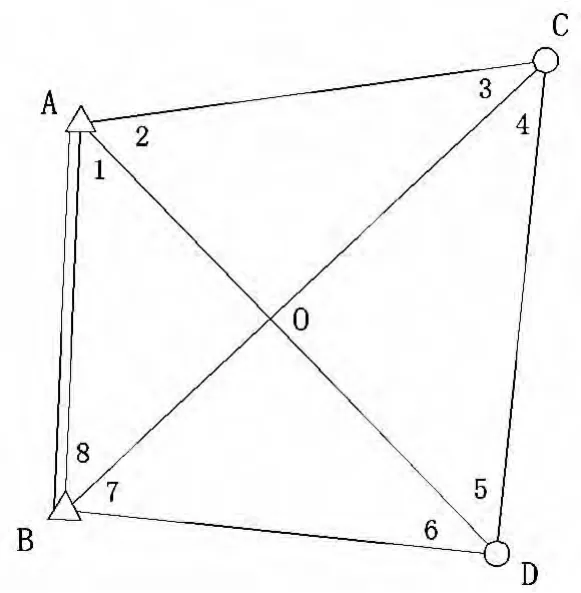
圖3 大地四邊形

解：以D點為極，BD為起算邊，分別按△DAB、△DCA、△DCB順序轉個圈，推算出的BD邊應等于BD,平差值極條件方程式為：

以上步驟可只用來審核，直接列出的線性形式極條件方程如下：

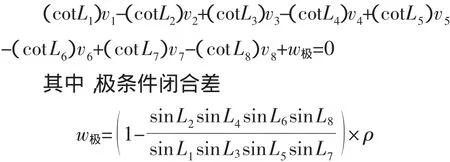
該極條件方程中，改正數v（ii=1，2…，8）前的系數為其相應觀測值的余切值，符號“＋”“、－”交替，以虛交點0為頂點，相似位置符號相同，如L1、L7、L5、L3位置（推算方向前進邊對應角度）對應符號均為“＋”，L8、L6、L4、L2位置（推算方向后視邊對應角度）對應符號均為“－”。閉合差表達式中，相對平差值方程表達式，分子分母換位置，符合規律口訣所述。

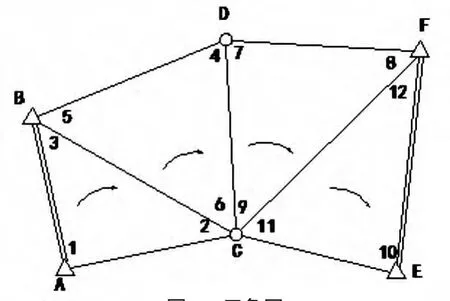
圖4 三角網

解：基線條件，即邊長附和條件。如圖所示，從AB一條已知邊 出發，根據正弦定理，沿如圖所示箭頭方向推算至另一條已知邊EF，用AB表示的推算EF邊理應等于已知邊長，整理得基線平差值方程：

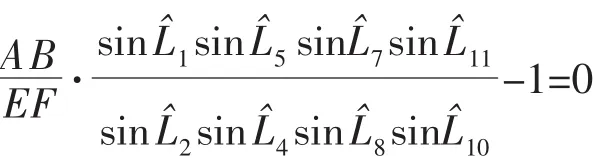
式中，AB、EF為已知邊長。上述推導過程和基線平差值方程可僅用來審核，事實上，可直接根據規律寫出基線條件方程：

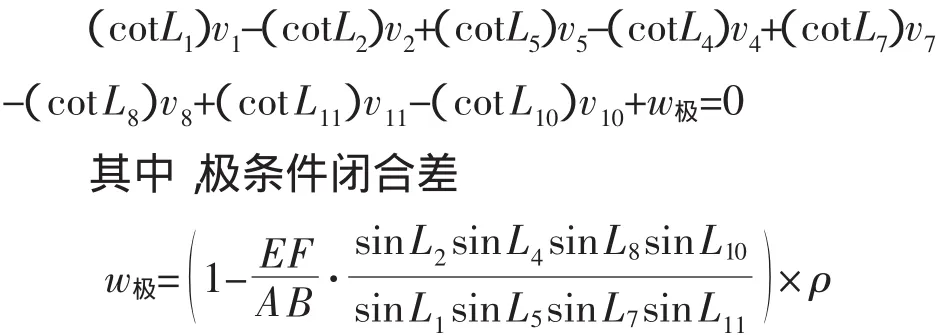
該極條件方程中，改正數v（ii=1，2…，12）前的系數為其相應觀測值的余切值，符號“＋”、“－”交替，且只出現和正弦定理推算相關的角度值，如L1、L2、L4、L5、L7、L8、L10、L11這 8 個角度。以 AB 為起算邊推算，相似位置符號相同，如 L1、L5、L7、L11位置（推算方向前進邊對應角度）對應符號均為“＋”，L2、L4、L8、L10位置（推算方向后視邊對應角度）對應符號均為“－”。閉合差表達式中，相對平差值方程表達式，分子分母換位置，符合規律口訣所述。

在平差中，經常需要求出未知邊平差值的相對中誤差以評定精度，而要想求定未知邊平差值的相對中誤差必須寫出其權函數式，利用線性化的權函數式中的系數求相對中誤差。如題目要求寫出CE邊平差值 的權函數式，如圖，從一條已知邊AB（也可從EF）出發，根據正弦定理，從左到右推算至CE：

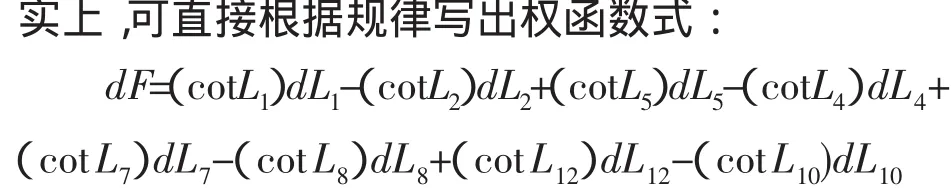
該權函數式中，改正數dLi（i=1，2…，12）前的系數為其相應觀測值的余切值，符號“＋”、“－”交替，且只出現和正弦定理推算相關的角度值，如L1、L2、L4、L5、L7、L8、L10、L12這 8 個角度。以 為起算邊推算，相似位置符號相同，如 L1、L5、L7、L12位置（推算方向前進邊對應角度）對應符號均為“＋”，L2、L4、L8、L10位置（推算方向后視邊對應角度）對應符號均為“－”，符合規律口訣所述。

四、結語

通過實例論證可知，以上極條件列立規律簡單明了、抓住本質、容易掌握、易于應用，適用于中點三角形、中點多邊形、大地四邊形、基線等所有獨立測角網極條件方程列立情形，此外，它還適用于邊長函數式的列立及線性化為權函數式從而進行精度評定等方面的應用，為高效解決這類難題提供了方法。

［1］肖飛.《測量平差》教材“極條件線性化”規律的研究與應用［J］.礦山測量，2012（6）:102～104.

［2］武漢大學測繪學院平差學科組.誤差理論與測量平差基礎［M］.武漢:武漢大學出版社，2009.

［3］劉仁釗.測量平差［M］.鄭州:黃河水利出版社,2007.