基于小波奇異性檢測的發動機故障診斷方法研究*

肖云魁，喬 龍，張玲玲,2，趙慧敏，楊青樂

(1.軍事交通學院汽車工程系，天津 300161； 2.軍械工程學院火炮工程系，石家莊 050003)

前言

信號的奇異點往往包含故障引起的撞擊、振蕩、摩擦和結構變形等重要信息[1]。二進離散小波變換不但可以準確地確定奇異點的位置，而且可以檢測信號奇異性特征[2]。數學上常用Lipschitz指數來定量描述信號的局部奇異性[3]，然而通過二進離散小波變換計算出的Lipschitz指數不夠精確且不含有與故障程度密切相關的能量信息，模極大值的平方和指示能量的物理意義則更明確[4]。本文中提出了模極大值點能量的概念來描述某一段信號的奇異性，并應用到發動機曲軸軸承的故障診斷中。

發動機激勵源眾多[5]，從機體上所得到的振動信號是內部多個運動部件綜合激勵的結果。僅從振動信號來判斷故障存在一定的困難。某些部件在工作中對系統施加的沖擊力與配氣相位密切相關，因此通過提取特定時間段的信息(抽區間采樣)，對其進行分析可以有效實現特定部件運行狀態信息的的分離，提取出故障信號特征。

1 小波奇異性檢測原理

對信號進行奇異性檢測包括對奇異點的定位和確立奇異性指標的大小兩個方面[6]。

1.1 奇異點的定位

設ψ(t)是小波母函數。當分析機械振動信號時，一般可選擇具有二階消失矩的小波函數[7]，本文中選擇db2小波作為小波母函數。函數f(t)∈L2(R)關于ψ(t)的二進離散小波變換為

(1)

式中：2j為小波變換尺度；W為小波變換系數。當小波變換尺度為s時，如果存在一點b0，使b0的某一鄰域內的任意點b，均有|Ws(b,ψ(t))|≤|Ws(b0,ψ(t))|，則稱(s,b0)為小波變換的模極大值點[8]，它與f(t)的奇異點存在對應關系，Ws(b0,ψ(t))是小波變換模極大值。

在低尺度下小波變換的模極大值點與突變點對應準確，但容易受噪聲的影響產生許多偽極值而影響判斷；隨著尺度的增加，噪聲的小波變換幅度以指數規律迅速衰減[9-10]，由于機械振動信號的峰值點和突變尖點的Lipschitz指數通常為正[1]，其小波變換的幅值隨尺度的增加而增加，從而分離出模極大值點和噪聲，但大尺度下模極大值點對奇異點的定位相對較差。因此，須進行多尺度分析方可有較好的效果。

1.2 奇異性指標的確立

二進離散小波變換為了使變換具有時不變性，只作尺度上的二進離散，對不同尺度上的時間參數進行等間隔采樣。然而，尺度區間的二進離散在許多情況下顯得過于粗糙，從而計算出的Lipschitz指數不夠精確，不能很好地區分是正常點還是異常點[4]，而且用Lipschitz指數不能區分同類型但突變程度不同的突變點。而求取可以指示能量大小的模極大值的平方和，計算簡單且物理意義更明確。因此，可用信號模極大點的能量之和來描述該信號整體的奇異性，能量之和越大，說明整體信號奇異性越強，反之則越小。

模極大值點能量之和為

(2)

式中：f為待分析的信號；s為小波變換的尺度；N為模極大值點的點數；ti為第i個模極大值點出現的時刻；ψ為小波母函數；W為模極大值。

2 仿真算例

本文中以一個含有3個階躍信號的函數f0(t)為例，加入高斯白噪聲fnoise(t)建立仿真信號f(t):

f(t)=f0(t)+fnoise(t)

fnoise(t)為加入的信噪比為35db的白噪聲，時域波形如圖1(a)所示。從信號定義和時域波形可以看出，信號在時刻32、64、128處是突變點，在時刻128處突變程度是32和64處的2倍。而理論上沖擊點的Lipschitz指數均為0。選用db2小波作為母函數，小波變換尺度為21、22、23，經過計算得到奇異點的Lipschitz指數均為0.098 3。所以利用二進離散小波變換得出的Lipschitz指數作為振動信號的奇異性指標不夠精確；而且未能體現出信號奇異點的能量。

下面采用模極大值點能量|Wsf(ti,ψ)|2來衡量信號的奇異性。選用db2小波對其進行3層小波分解，分解尺度為21、22、23的模極大值點分別如圖1(b)～圖1(d)所示。

由圖可見：在分解尺度為21時由于噪聲較多，模極大值圖中產生了許多偽極值點，不能正確判斷出奇異點的位置；當分解尺度增加到22時噪聲點數明顯減少，可以清晰地看出突變點的位置，并且時刻128點處模極大值大約是時刻32和64處的2倍，說明時刻128處的能量是其他兩點處的4倍；但是當尺度繼續增大到23時，奇異點的位置開始發生較為明顯的偏移，這是因為小波變換計算過程是信號與小波函數進行卷積運算的過程，當小波函數尺度較大時，信號的時域分辨率較差造成對奇異點定位不準確。因此采用模極大值點的能量來描述奇異性時，在多尺度下綜合分析不僅能精確指出奇異位置，而且可以衡量奇異點能量的大小。

3 實例分析

3.1 試驗設置

本文中以東風EQ2102型柴油發動機作為研究對象，選取第4道曲軸軸承為試驗軸承，分別設置不同曲軸軸頸與軸承配合間隙以模擬各種磨損狀態。由于曲軸具有很高的剛度，當僅有1道軸承間隙增大時，它承擔的載荷會減小，相鄰的軸承分擔的載荷增大，隨著發動機的運轉，相鄰軸承的間隙也會發生相應的變化。為了更加符合實際情況，同時設置第3、4、5道曲軸軸承為故障軸承。故障設置情況如表1所示。

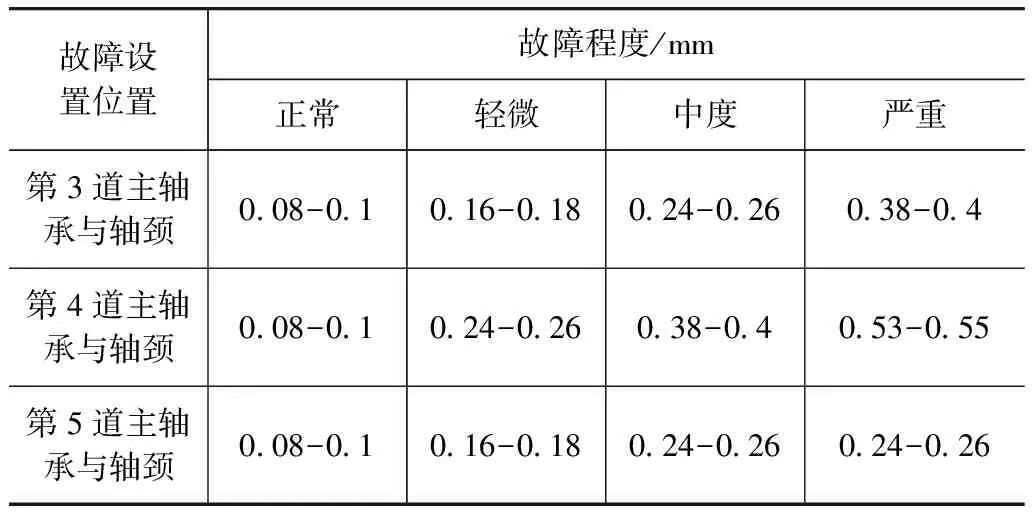
表1 發動機曲軸軸承不同配合間隙設置

測量發動機在曲軸軸承不同配合間隙條件下不同測點的振動信號，測點a～d分布如圖2所示，4個測點與第4道曲軸軸承在一個平面內。同時采集飛輪殼齒圈脈沖信號和第1缸噴油壓力信號分別用以計算發動機轉速和抽區間采樣，采集發動機各缸上止點信號，發動機空載運行。為了確定最佳故障診斷轉速，選擇800、1 300、1 800和2 100r/min為試驗轉速。采樣頻率設置為20kHz。

3.2 抽區間采樣

抽區間采樣是采集對應于發動機每一循環中特定時間段內的振動信號，與某個感興趣的瞬態沖擊力相對應，然后采用一些分析方法進行特征提取[3]。對于發動機某一道曲軸軸承的故障來說，它對應的氣缸做功時故障特征會表現得更為明顯。同時為了保證數據的穩定性，抽取發動機連續4個工作循環第4缸做功階段的信號進行分析。下面以發動機正常工況下轉速為1 800r/min時測點b處的振動信號為例，說明抽區間采樣的過程：

(1) 連續尋找5個噴油時刻 設定一個閾值，當噴油壓力信號的幅值大于該值時即認為該點為噴油時刻(本文中設定1為閾值)，連續尋找5個噴油時刻，如圖3(a)所示，則每2個噴油時刻之間發動機完成了一次工作循環；

(2) 抽取連續4個工作循環的振動信號 由于該型發動機噴油提前角為20°，將振動信號中5個噴油時刻間的數據往后推移74個數據點(采樣頻率為20kHz，發動機轉速為1 800r/min時噴油提前角對應約74個數據點)，即為發動機連續4個工作循環的振動信號，如圖3(b)所示，雙箭頭標注為做功序號(下同)；

(3) 抽取連續4個工作循環中第4缸做功階段的振動信號 根據6缸發動機做功順序：1-5-3-6-2-4，將通過步驟(2)抽取的每一工作循環的振動信號平均分成6段，抽取最后一段作為第4缸做功階段的振動信號(約為222個點)，連接在一起完成抽區間采樣，如圖3(c)所示。

3.3 試驗數據的分析

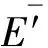
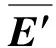
表2 曲軸軸承不同技術狀態下對比

選擇db2小波進行5層二進離散小波變換，提取每一層小波變換的模極大值點。轉速為1 800r/min時測點b處不同技術狀態下的模極大值如圖5所示，限于篇幅圖中只列出了小波變換尺度為21、23和25時的模極大值點。

由圖可見：縱向分析，可以明顯看出隨著尺度的增加，模極大點的數目依次減少但幅值增加，說明噪聲隨著尺度的增加急劇衰減，而突變信號由于Lipschitz指數為正，模極大值隨尺度的增加而變大，與噪聲表現正好相反，因此隨著尺度的增加噪聲和奇異點得以分離；橫向對比，隨著曲軸軸承與軸頸配合間隙的增大，在同一尺度下總體上模極大值越來越大。除此之外，根據小尺度分解時模極大值點對奇異點定位精確的特點，從分解尺度為21的模極大值圖中可以看出，當曲軸軸承出現磨損故障的情況下，每個做功階段中第4缸開始做功時模極大值開始增大，如圖5(b)～圖5(d)中222點、444點、666點處左右。這是因為發動機運轉過程中，當某一缸從壓縮行程換至做功行程時活塞換向，而曲軸軸承與軸頸的配合間隙超出正常范圍后，連桿帶動曲軸旋轉時對軸承的撞擊加劇，表現為缸體信號奇異性增強。

圖5中分解尺度為25時極大模值點的點數已經明顯減少、幅值穩定，而且相對于小尺度分解時模極大值點的偏移程度可以接受，因此確定在該尺度下計算模極大值點能量之和進行奇異性分析。曲軸軸承每種技術狀態下隨機選取40組樣本，每組樣本的E值如圖6所示。

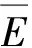
表3 曲軸軸承不同技術狀態下對比

為了確定最佳測試轉速，本文中利用同樣方法對發動機在怠速800r/min、中速1 300r/min和高速2 100r/min時分別進行了分析，發現在中低速(800、1 300r/min)時信號的模極大值點平均能量與故障程度之間并沒有規律，而在高速(2 100r/min)時與中高速(1 800r/min)一樣有規律。這是由于發動機機體沉重，運轉時其慣性與速度有很大關系，速度越高慣性越大，連桿帶動曲軸旋轉時對軸承的撞擊越大，當速度較低時，撞擊力小，經過缸體的低通濾波作用其奇異性并沒有通過缸體信號體現出來。

同樣本文中分析了發動機缸體右側(測點c)和油底殼(測點d)、缸蓋處(測點a)的振動信號的奇異性，都沒有良好的規律性。這是由發動機的結構決定的：從發動機后方觀察發動機運轉時，連桿帶動曲軸做逆時針旋轉運動，當被測軸承對應的氣缸開始做功時活塞下行，曲軸對軸承左側形成瞬態強烈沖擊，位于缸體外部左側的振動傳感器正好捕捉到這一信號。當曲軸撞擊軸承右側時，氣缸已完成做功行程，撞擊已經明顯減弱。而油底殼和缸蓋由于距離激勵源較遠，信號的奇異性也不顯著。

4 結論

(1) 利用模極大值點能量來描述信號奇異性的方法計算簡單、意義明確，抽區間采樣能有效縮短分析數據的長度，突出局部時間段的信號特征，兩種方法的結合能有效區分出曲軸軸承的技術狀態。

(2) 對發動機曲軸軸承進行故障診斷時，利用模極大值點能量進行奇異性檢測的最佳轉速是中高速，最佳診斷部位為發動機缸體左側。

[1] 賀銀芝,沈松,劉正士,等.基于小波變換的奇異性檢測在發動機連桿軸承故障診斷中的應用[J].北京工業大學學報,2000,26(4):72.

[2] 龐茂,周曉軍,胡宏偉,等.基于解析小波變換的奇異性檢測和特征提取[J].浙江大學學報,2006,40(11):1994-1997.

[3] 林京,屈梁生.基于連續小波變換的奇異性檢測與故障診斷[J].振動工程學報,2000,13(4):523-529.

[4] 余同輝,閆河,何莉,等.基于小波奇異性理論的輸油管道泄漏檢測與定位方法[J].計算機技術與應用,2009(9):135.

[5] 賈繼德,陳榮鋼,陳劍.基于抽區間采樣的內燃機狀態監測方法研究[J].內燃機工程,2005,26(6):72-75.

[6] 關山,胡全.小波奇異性檢測理論在齒輪故障診斷中的應用[J].煤礦機械,2008,29(8):188-190.

[7] 褚福磊,彭志科,馮志鵬,等.機械故障診斷中的現代信號處理方法[M].北京:科學出版社,2009:58-70.

[8] 胡昌華,張軍波,夏軍,等.基于MATLAB的系統分析與設計[M].西安:西安電子科技大學出版社,1999:210.

[9] 李曙光,張梅軍.小波去噪與奇異性檢測相結合診斷動靜件短暫碰磨故障發生區間[J].機械設計,2010,27(10):80.

[10] Anend K Soman, Vaidyanathan P P. On Othormormal Wavelates and Paraunitary Filter Banks[J]. IEEE Trans. S. P.,1993,41(3):1170-1183.