基于SORA方法的汽車耐撞性優(yōu)化*

陳吉清,鄭炳杰,蘭鳳崇,馬芳武

(1.華南理工大學機械與汽車工程學院,廣州 510640; 2.華南理工大學，廣東省汽車工程重點實驗室，廣州 510640;3.浙江吉利汽車研究院,杭州 311228)

前言

汽車的碰撞分析是一個復雜的工程技術，在實際工程中由于材料性質(zhì)、制造工藝和結構外部環(huán)境的復雜性以及人為假定等因素的存在，使設計過程中需要考慮的參數(shù)存在很大的不確定性，因此在研究碰撞問題的確定性設計的同時，也有必要關注其結構可靠性，降低目標對設計變量的靈敏性[1]。

傳統(tǒng)的可靠性優(yōu)化方法往往是將可靠性約束轉(zhuǎn)化成確定性約束，利用某種算法尋優(yōu)，最后采用蒙特卡羅法進行可靠性分析，評估優(yōu)化效果。這種雙循環(huán)策略的缺點是計算成本高，為改善可靠性分析的計算效率，文獻[2]和文獻[3]中提出了序列優(yōu)化與可靠性評估(SORA)方法，這種方法將可靠性分析與確定性優(yōu)化分開，依次進行，通過在循環(huán)迭代中修正約束的方法逼近可靠性解。由于SORA方法的單循環(huán)策略明顯改善了優(yōu)化效率，該算法在某些領域已經(jīng)得到了廣泛應用，包括飛航導彈和飛機設計等復雜工程問題[4-8]。

本文中將SORA方法引入到汽車前端碰撞的可靠性分析中，同時借助Kriging[9-10]插值技術，建立了碰撞響應的Kriging代理模型，對汽車前端進行輕量化優(yōu)化，得到符合可靠性設計的優(yōu)化結果，有效地提高了計算效率和精度。

1 序列優(yōu)化與可靠性評估

一般可靠性優(yōu)化設計模型可描述為

(1)

式中：F(·)表示目標函數(shù)；d為確定性設計變量；x為隨機變量；Pr為滿足括號內(nèi)邊界條件的概率；G(·)為約束條件函數(shù)；R為要求達到的可靠度。

傳統(tǒng)的可靠性優(yōu)化方法將任意分布參數(shù)的可靠性約束等價轉(zhuǎn)化為

G+βσg≥0

(2)

式中：β為可靠度R對應的可靠性指標；σg為響應的方差。

該優(yōu)化過程須要計算響應的均值、方差和隨機約束的概率，以評估響應的可靠性，常用的方法有蒙特卡羅法[1]、一次二階矩法[11]等。它是一個雙循環(huán)策略，其外部循環(huán)是確定性優(yōu)化，內(nèi)部的可靠性分析嵌套在優(yōu)化循環(huán)中，每次迭代皆須進行完整的可靠性分析，計算效率低。為彌補這一缺陷，文獻[2]中提出了一種單循環(huán)策略的SORA方法，它將可靠性分析和確定性優(yōu)化分離，用上一次可靠性的分析結果來修改下一次確定性優(yōu)化的約束條件，這樣大大提高了可靠性分析的效率。

一個包含兩個隨機設計變量的優(yōu)化模型為

(3)

式中：μx為隨機變量的均值，μx=(μx1,μx2)。

狀態(tài)函數(shù)為

G(x1,x2)=0

(4)

假設x1和x2為相互獨立的正態(tài)分布變量，現(xiàn)對其進行當量標準正態(tài)化變換：

x=(x-μx)/σx

(5)

式中：σx表示隨機變量的標準差，σx=(σx1,σx2)。

定義可靠性指標為

(6)

則可靠度可表示為

R=φ(β)

(7)

將式(5)代入式(4)可得到在標準正態(tài)分布空間的約束界面，如圖1所示，進一步求解式(3)中的目標函數(shù)F(·)的最小值，即能在界面上搜索到設計驗算點MPP。點(μ1,μ2)就是該約束條件下的確定性分析的最優(yōu)解。

如圖1所示，MPP處的正態(tài)分布曲線表示變量的概率分布密度，可見確定性分析的可靠度大約為50%，對于可靠性分析來說，其可靠度太低。由設計要求的可靠度R，可得到概率性失效點MPPi，它即為變量可行性區(qū)域的邊界點。為達到可行性要求，變量的可行性區(qū)域應該全部落在確定性邊界以內(nèi)。因此須進行約束修正，約束的移動距離用s表示。此時的確定性約束修正為

G(μx1-s1,μx2-s2)≥0

(8)

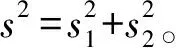
于是，第k次循環(huán)的優(yōu)化模型可表示為

(9)

每一次循環(huán)的可靠性相對上一次循環(huán)得到了改善，若可靠性仍達不到設計要求，則繼續(xù)修正約束條件，直到計算收斂，其流程如圖2所示。以此類推，多個變量的優(yōu)化模型也能通過同樣的序列化循環(huán)方法，在較短的時間內(nèi)求解得到可靠性結果。SORA方法相對于傳統(tǒng)可靠性優(yōu)化的優(yōu)勢在于，采用單循環(huán)策略很好地集成了可靠性分析和確定性優(yōu)化，并且在進行可靠性分析時，將前一輪循環(huán)得到的最優(yōu)解，作為下一輪循環(huán)中優(yōu)化的初始點，前一輪循環(huán)得到的逆MPP，作為下一輪循環(huán)中搜索逆MPP時的初始位置，減少可靠性分析的次數(shù)，提高優(yōu)化效率。

2 汽車耐撞性仿真模型與代理模型

2.1 仿真模型與試驗設計

圖3為汽車前端的數(shù)值模型，包括整車模型中發(fā)動機艙防火墻以前的部分，后面部分由于在碰撞過程中變形較小，對分析前防撞系統(tǒng)的耐撞性影響較小，用一個集中質(zhì)量單元代替。模型被截斷處的節(jié)點定義為節(jié)點集，通過RBE單元與質(zhì)量單元連接起來。質(zhì)量單元處施加了一個運動約束，約束曲線為整車碰撞的B柱下方輸出頻率為1 000Hz的位移-時間曲線。這樣就確保了該模型的總質(zhì)量和運動狀態(tài)與整車模型保持一致。該有限元模型包含184 991個節(jié)點，192 035個單元，其中三角形單元個數(shù)為8 711，占總單元數(shù)的4.5%，符合三角形單元不超過5%的精度要求。單元之間無穿透、干涉現(xiàn)象存在。

在構造代理模型的過程中，試驗點的選取非常重要，良好分布的試驗點有利于更加精確地反映響應和設計變量之間的關系[12]。相反，不具有代表性的試驗點則可能導致所構造的模型失真。本文中采用拉丁超立方抽樣方法，通過控制抽樣點的位置，避免出現(xiàn)小鄰域內(nèi)被多次抽樣，且無被忽略區(qū)域。若進行n次抽樣，把m個隨機變量分別等分為n個區(qū)間，則整個抽樣空間就被劃分成n個m維區(qū)間。對于每個變量，保證n次隨機抽樣一定分別落在各小區(qū)間，因此抽樣點被等概率地分布到整個隨機空間內(nèi)。

運用拉丁超立方抽樣方法選取了20組樣本點，各方案的試驗結果見表1。其中方案0表示優(yōu)化前的狀態(tài)；T1～T5為設計變量，如圖4所示，分別表示前橫梁、吸能盒內(nèi)、外板和前縱梁內(nèi)、外板的板厚；M為被優(yōu)化零件的總質(zhì)量；E為碰撞過程中吸收的總內(nèi)能。

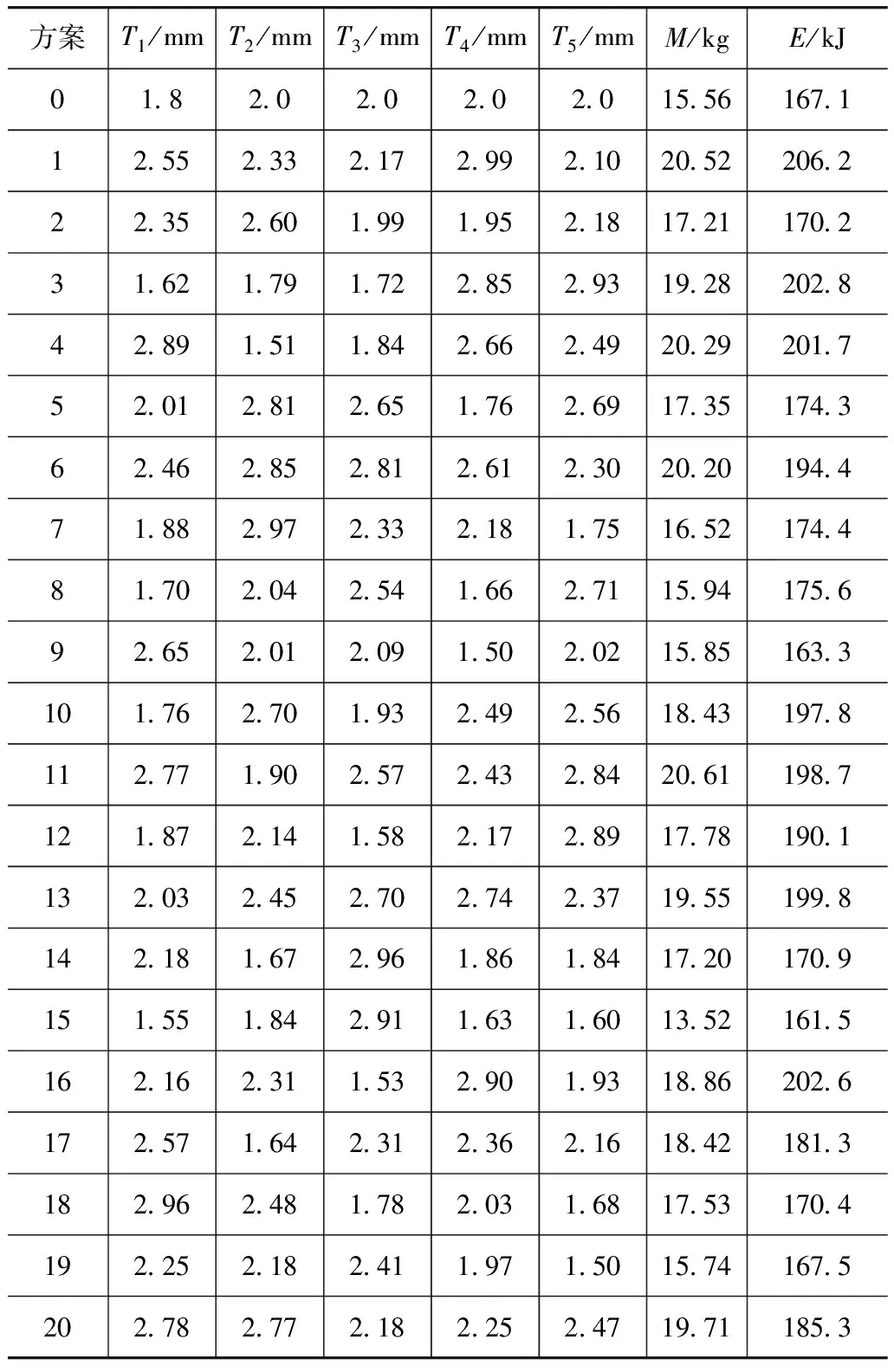
表1 拉丁超立方試驗設計表

2.2 建立Kriging代理模型

Kriging方法是一種無偏插值方法[13-14]。Kriging近似模型假設系統(tǒng)的響應由一個參數(shù)模型和一個非參數(shù)隨機過程聯(lián)合構成：

y(x)=F(x)+Z(x)

(10)

式中：F(x)為參數(shù)模型，為多項式回歸方程；Z(x)為隨機分布，提供對模型局部偏差的估計，具有以下特性：

E[Z(x)]=0

(11)

(12)

(13)

式中：xi和xj表示樣本點中的任意兩個點；R(θ,xi,xj)為帶參數(shù)θ的相關函數(shù)。

任意一個待測點xn通過已知的抽樣點來預測，用抽樣點的響應矩陣Y的線性組合表示為

(14)

Kriging的無偏特性要求預測誤差的均值為零，并且預測方差應最小化，于是綜上所述能求得系數(shù)矩陣c。HyperWorks軟件中的HyperKriging工具箱集成了上述代理模型的構建程序，通過調(diào)用該程序可計算得到Kriging近似模型。

半?yún)?shù)化的Kriging模型無須建立一個特定的數(shù)學模型[9]，相對于參數(shù)化模型而言，Kriging模型的應用更加靈活和方便。圖5為經(jīng)典數(shù)學函數(shù)“墨西哥帽子”的各種擬合試驗，“墨西哥帽子”的解析方程式為

z=sinr/r

(15)

圖5(a)為式(15)用Matlab軟件模擬的解析解；圖5(b)為運用Kriging方法通過20個抽樣點插值構造的模擬解；圖5(c)為用二次響應面構造的模擬解，采用的抽樣點與圖5(b)相同。通過這個簡單的非線性算例，可以看出Kriging方法對高非線性問題的模擬精度和整體適應性優(yōu)于二次響應面方法。

將試驗數(shù)據(jù)導入HyperWorks，通過以上求解程序求得吸能量E的Kriging響應模型。直觀上可以預見板件的質(zhì)量與板厚的函數(shù)關系為線性關系，因此采用最小二乘法對試驗數(shù)據(jù)進行線性擬合，即得到總質(zhì)量M與設計變量T之間的函數(shù)關系為

M=1.98T1+0.38T2+0.69T3+3.02T4+1.79T5

(16)

3 SORA優(yōu)化與驗證

3.1 SORA優(yōu)化

本算例的優(yōu)化目標是：在輕量化的同時要求吸能效果最佳。為達到輕量化目標，制定以下約束：對吸能部件總質(zhì)量進行約束，要求其至少能減質(zhì)量1kg，同時希望碰撞過程吸收的內(nèi)能最大，即減質(zhì)量對吸能的削弱影響最小。優(yōu)化問題用以下數(shù)學模型描述為

(17)

假設板厚T為服從正態(tài)分布的隨機變量，令其方差為0.006，要求約束滿足可靠度為95%，將設計目標和約束條件代入圖2的SORA流程進行計算，經(jīng)過3次迭代達到收斂，迭代過程如表2所示。其中可靠性邊界解表示正態(tài)分布變量對應的目標解集中，發(fā)生概率為Pr=1-R處的邊界解。第1次確定性優(yōu)化所得到的解一般不滿足設定的可靠性條件，這一步得到的目標解M剛好落在約束邊界，但可靠性邊界解不符合約束條件，因此通過尋找逆MPP點，確定s的值，對約束進行修正進入第2次迭代。經(jīng)過第2次優(yōu)化后，M的目標解往可行區(qū)域內(nèi)移動，可靠性得到改善，但可靠性邊界解仍不符合要求，即沒有達到可靠度為95%的要求，需進一步修正約束。第3次迭代后，M的可靠性邊界解落在可行區(qū)域內(nèi)，計算收斂。

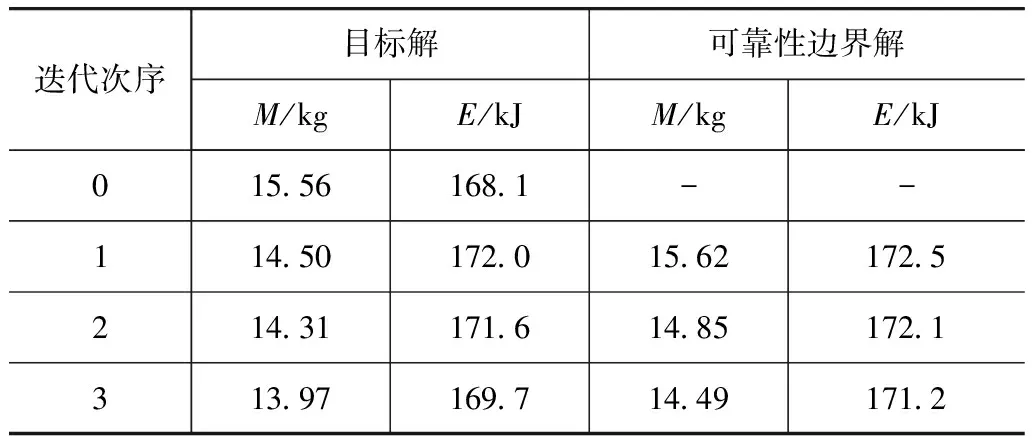
表2 迭代過程

文獻[1]中采用了傳統(tǒng)的可靠性優(yōu)化方法，在進行了確定性優(yōu)化后，采用蒙特卡羅法抽取了100組設計變量對優(yōu)化結果進行可靠性評估，若評估結果符合要求，計算終止；若評估結果不符合要求，須返回到整個優(yōu)化流程的第一步，重新進行確定性優(yōu)化和可靠性評估。本文中采用SORA方法，僅進行了3次約束修正即完成了可靠性優(yōu)化過程，其計算成本相對傳統(tǒng)可靠性優(yōu)化明顯降低。

3.2 結果驗證

經(jīng)過SORA優(yōu)化后的設計變量如表3所示。將其預測值與有限元仿真的試驗值進行對比驗證，結果如表4所示。

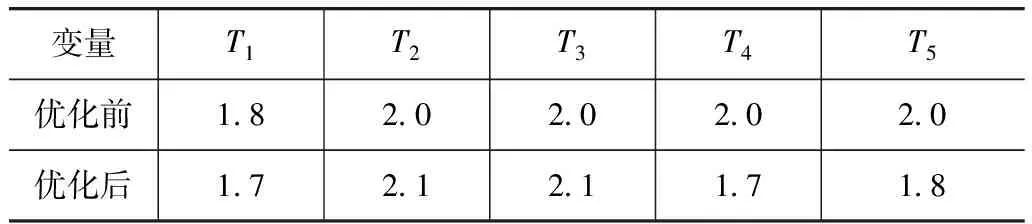
表3 設計變量優(yōu)化結果 mm

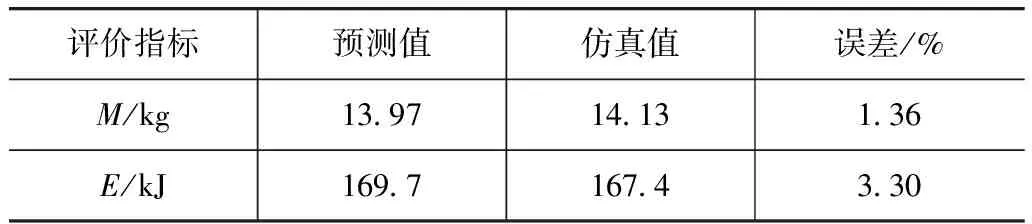
表4 預測結果驗證

從表4可以看出，質(zhì)量M的相對誤差很小，這是因為質(zhì)量與板厚是線性關系，用最小二乘法擬合能精確擬合線性問題。Kriging模型擬合的吸能量E也達到了很高的精度，可以認為采用的代理模型有效。從優(yōu)化結果看，吸能部件的質(zhì)量從15.56kg下降到14.13kg，減質(zhì)量1.43kg，達到了優(yōu)化目標；優(yōu)化后的吸能量為167.4kJ，相對原模型提高了0.3kJ，達到了預期目標，即減質(zhì)量對吸能效果影響最小。以上結果表明，Kriging結合SORA的優(yōu)化方法有效。

為驗證結果的可靠性，采用蒙特卡羅描述性抽樣獲得1 000組設計變量，將1 000組設計變量分別代入代理模型中計算響應的均值和方差，判斷約束的失效概率。圖6給出了質(zhì)量M和吸能量E的頻數(shù)直方圖。

如圖6所示，試驗結果大致呈正態(tài)分布。質(zhì)量M大于14.5kg的試驗次數(shù)為44次，即失效概率為4.4%，符合可靠度為95%的要求。同時，質(zhì)量M和吸能量E試驗值的均方差值Dev相比其均值非常小，表明試驗數(shù)據(jù)偏離均值的程度很小，優(yōu)化結果的響應對該設計點自變量的敏感度不高，該優(yōu)化設計具有較高的魯棒性。綜上所述，本文中采用的優(yōu)化方法具有較高的精度，并且優(yōu)化結果符合可靠性要求。

4 結論

(1) 將SORA方法引入到汽車耐撞性的可靠性優(yōu)化，通過理論分析和實例分析，驗證表明SORA方法可以有效地處理耐撞性優(yōu)化問題。

(2) 通過與傳統(tǒng)雙循環(huán)優(yōu)化策略的對比，表明SORA方法在處理可靠性優(yōu)化問題時更高效。

(3) SORA方法的關鍵在于不斷修正約束去逼近可靠性約束，當目標函數(shù)與約束條件的非線性程度太高或者出現(xiàn)不連續(xù)時，約束的修正和確定性優(yōu)化會影響可靠性指標的收斂。本文中構造了Kriging代理模型，避免了原模型的復雜性，保證了迭代的收斂，同時具有較高的模擬精度。

[1] 謝然,蘭鳳崇,陳吉清,等.滿足可靠性要求的輕量化車身結構多目標優(yōu)化方法[J].機械工程學報,2011,47(4):117-124.

[2] Du X, Chen W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design[J]. Journal of Mechanical Design,2004,126(2):225-233.

[3] Yin X, Chen W. Enhanced Sequential Optimization and Reliability Assessment Method[J]. Structure and Infrastructure Engineering,2006,2(3):261-275.

[4] 夏青,蔡洪,張士峰.可靠性優(yōu)化方法在飛航導彈多學科設計優(yōu)化中的引用[J].彈箭與制導學報,2010,30(1):40-42.

[5] 王宇.基于不確定性的優(yōu)化方法及其在飛機設計中的應用[D].南京:南京航空航天大學,2010.4.

[6] 黃洪鐘,余輝,袁亞輝,等.基于單學科可行法的多學科可靠性設計優(yōu)化[J].航空學報,2009,30(10):1871-1876.

[7] 陳仁伍,谷良賢,龔春林.一種基于SORA方法的多學科可靠性設計方法[J].機械強度,2008,30(1):37-40.

[8] 余輝.基于協(xié)同優(yōu)化和單學科可行法的可靠性優(yōu)化設計[D].成都:電子科技大學,2008.6.

[9] 高云凱,孫芳,余海燕.基于Kriging模型的車身耐撞性優(yōu)化設計[J].汽車工程,2010,32(1):17-21.

[10] 王國春,成艾國,胡朝輝,等.基于Kriging模型的汽車前部結構的耐撞性優(yōu)化[J].汽車工程,2011,33(3):208-212.

[11] 孟廣偉,趙云亮,李鋒,等.含多裂紋結構的斷裂可靠性分析[J].吉林大學學報(工學版),2008,38(3):614-618.

[12] 張建國,蘇多,劉英衛(wèi).機械產(chǎn)品可靠性分析與優(yōu)化[M].北京:電子工業(yè)出版社,2008:109-115.

[13] Sakata S, Ashida F, Zako M. Structural Optimization Using Kriging Approximation[J]. Computer Methods in Applied Mechanics and Engineering,2003,192:923-939.

[14] 高月華.基于Kriging代理模型的優(yōu)化設計方法及其在注塑成型中的應用[D].大連:大連理工大學,2009,4.