基于二元離散選擇模型的高校大學生考試掛科原因分析

丁詠梅，李壽貴，胡 杰，余 東

（武漢科技大學 理學院信息與計算科學系，湖北 武漢 430065）

基于二元離散選擇模型的高校大學生考試掛科原因分析

丁詠梅，李壽貴，胡 杰，余 東

（武漢科技大學 理學院信息與計算科學系，湖北 武漢 430065）

基于Probit二元離散選擇模型對影響大學生掛科的關鍵因素進行了實證分析，結果表明，學生學習時間對掛科與否有重大影響，而性別、健康狀況和高考成績對掛科與否影響并不顯著。文章的最后，針對學生掛科現象，給出相應建議。

二元離散選擇模型；效用模型；似然估計

進入大學，意味著未來有著高科技含量的工作、優厚的待遇、高尚的素養和品德。相較于中學，大學生活的確相對寬松，只要修滿學位所需的課程和學分，就可以拿到相應的學位證和畢業證，自由度很大。同時各高校實現聯合培養模式也為現代大學生提供了更多獲取知識、信息的渠道，各種社團、學會給每位大學生提供一個展示自我、鍛煉自身能力的平臺。大學教育讓每一位大學生盡可能做到人盡其學，各顯其能。而評價某門課程是否學好的標準，主要的方式仍然是考試成績。雖然象牙塔中的大多數學生都能明確學習目標、端正學習態度、不斷完善自身，但是，近些年，掛科現象也不容忽視。一方面，掛科意味著學生對本門課程的基本知識掌握不足，另一方面，掛科也意味著教育成本、成長成本的增加。

一、掛科原因的定性分析

綜合國內外關于大學生掛科原因，從定性的角度來分析，主要體現為以下幾點：（1）學習目標不明確。大學的業余時間充足，常有豐富多彩的社團活動和各式各樣的比賽。一部分同學把精力全部寄托于社團活動，本末倒置，不再學習。（2）自控能力差，沉迷網絡。網絡的誘惑是導致大學生掛科的重要原因。（3）盲目追求愛情。大學愛情美好而充滿幻想。但是很多人急于在大學擺脫單身，是一種攀比性戀愛心理在作怪。（4）打工分散精力。有一部分同學打工的目的是為了減輕家庭負擔，但是有些同學去打工，只是為了擁有更多的錢去吃喝玩樂。（5）課堂學習資源和信息欠缺。有研究表明，大量的由教師提供的網上課程資源與學生的低逃課率有關；另外，也有一些研究表明，講課前運用多媒體放映一些跟教學內容相關的幻燈片可能對學生的出勤率和對課堂的參與性有積極影響。（6）學校對于師資的分配不合理。有的班級學生人數過多影響學生學習環境。有跡象表明，當課堂人數增加時，學生的平均成績會出現下降。

二、掛科原因的定量分析

上面描述的大學生掛科原因涉及到的因素繁多，主次有待通過定量分析來確定，掛科以計數來定，即考查大學生的掛科門數。基于此，本文采取二元離散選擇模型對大學生掛科的原因進行理論分析和實證研究。

1.二元離散選擇模型。實際的社會生活中，我們常遇到二元選擇問題。如公共交通和私人交通的選擇問題，對某商品的購買決策問題，求職者對職業的選擇問題等。本文以學生掛科問題為例，如果某個學生的效用為，上標表示“選擇”結果，下標表示第i個個體。該效用是隨機變量，并且由學生掛科狀況所具有的屬性和決策個體所具有的屬性解釋。于是有。類似地，如果某個個體“選擇”不掛科，他的效用為，該效用是隨機變量，并且由不掛科所具有的屬性和決策個體所具有的屬性解釋。于是有。對于（1）和（2）模型中，效用是不可觀測的，我們能得到的觀測值仍是選擇結果，即0和1。但是，如果不可觀測的學生“選擇”掛科的效用大于不掛科效用，對應的觀測值為1；相反，如果不可觀測的相應的觀測值為0。將（1）與（2）相減：（3），記為：，我們可以對（4）進行計量分析和估計。對于學生“選擇”Yi=1的概率顯然應該有：

2.參數估計。模型（4）的被解釋變量不可觀測，顯然不能采用最小二乘估計，只能采用最大似然估計。為了實現模型的最大似然估計，就必須為μi*選擇一種特定的概率分布。兩種最常用的分布是標準正態分布和邏輯分布，于是形成了兩種最常用的二元選擇模型——Probit模型和Logit模型。無論是標準正態分布還是邏輯分布，由于他們是對稱的，存在F（-t）=1-F（t）（6）。式中F（t）表示概率分布函數。于是式（5）可以改寫為P（Yi=1）=P（Yi*＞0）=P（μi*＞-Xiβ）=1-P（μi*≤-Xiβ）=1-F（-Xiβ）=F（Xiβ）（7）。至此，可以得到模型（4）的似然函數，，對數似然函數為lnL=，對數似然函數最大化的一階條件為0（11）。式中fi表示概率密度函數。顯然，在樣本數據支持下，當（11）中的概率分布函數和概率密度函數已知時，求解該方程組，可以得到模型參數估計量。

3.實證分析。對于本文關于大學生考試掛科問題，據經驗分析和文獻研究的結果，影響大學生考試掛科的因素可能有高考成績（CEE）、平時學習時間（平均每周用于學習的時間，Stime）、性別（Sex）、健康狀況（Dbody）等。其中，性別和健康狀況為虛擬變量：

我們把學生掛科（Unpass）定義為被解釋變量，掛科為1，不掛科為0。選擇武漢科技大學2012級的部分同學作為樣本，選擇問卷調查的方式，列出5個變量，由學生主動填寫數據。發放問卷65份，回收65份，有效問卷62份，有效率為95%。為了進一步了解該樣本特征，本文作者從學校教務系統中調出該樣本的2013年秋季期末考試各門成績，并統計出平時成績，運用軟件eviews7.0，得出其J-B統計量為3.04（如表3.1所示），相伴概率約為0.22，因此在90%的顯著性水平下不能拒絕原假設，可以認為該樣本來自正態總體。

表3 .1 數據的分布檢驗

高考成績反映基礎水平，平時學習時間反映努力程度，健康反映身體基礎。基于以上數據收集，以不及格門數為被解釋變量，建立二元離散模型。統計結果如表3.2。

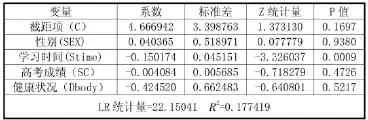
表3 .2 模型的參數估計結果

從表3.2中我們可以看出，性別和健康狀況對掛科影響并不顯著，高考成績對其略有影響，而學習時間直接影響著考試掛科。從R2看，模型擬合效果并不好。為了更直觀反映學習時間對掛科的影響，我們仍以考試掛科為因變量，以學習時間為自變量，建立模型，模型參數估計結果見表3.3。

表3 .3 估計結果

從以上結果中也可以看出，學習時間與考試掛科成負向關系，平時用的學習時間越少，掛科的可能性就越大，這也說明，欲減少掛科門數，必須在平時多投入時間，加強課后的學習和鞏固。表3.3中我們可以得出相應的預測模型為Unpass=1-@CNORM（-（2.257056-0.143409*Stime））（12）。從估計結果可以發現，檢驗擬合優度的R2檢驗統計量的值為0.367694，檢驗總體顯著性LR統計量的值為21.31330，表明模型具有較高的總體顯著性；通過模型3.1可以得知，如果得到一個樣本觀測值，也就是知道某位學生的平時學習時間（Stime），代入方程中便可以得出相應的掛科（Unpass）概率，如觀測值Stime=30時，代入方程右邊，計算括號內的值為2.04，查看標準正態分布表，對應于2.04的累積正態分布為0.979，于是，該學生掛科（Unpass）的概率為0.021。

對二元離散選擇模型的分析結果可以看出，高考分數對于掛科與否影響并不顯著，一個主要原因是大部分同學入學時的高考成績相當接近。性別和健康狀況對掛科與否也沒有重要影響。而學習時間對于學生掛科現象有顯著影響。因此，充足的學習時間是至關重要的。其次，要樹立正確的學習態度。大學是一個讓自己從稚嫩變成熟的過程，要不斷地從課堂、圖書館汲取知識的營養，豐富自己，以便造福于社會。同時作為教育管理者來說，建議豐富課堂教學手段，充實教學資源，且對班級人數進行合理規劃安排，為學生和老師創造理想的學習、教學環境。

[1]辛桂京，高藝倫.大學生掛科探析J].高校講壇，2012，（15）.

[2]李子奈，葉阿忠.高級應用計量經濟學[M].北京：清華大學出版社，2012：122-125.

[3]C.Ryan Kinlaw，Linda L Dunlap，Jeffrey A.D’Angelo.Relations between faculty use of online academic resources and student class attendance[J].Computer&Education，2012，（59）：167-172.

G640

A

1674-9324（2014）35-0151-02

中國學位與研究生教育學會2013年研究課題（編號：C1-2013Y05-045）；湖北省自然科學基金重點項目（2013CFA131）。

丁詠梅（1978-），女，武漢科技大學理學院副教授，系統工程博士。