基于偏微分方程圖像修補BSCB模型的應用

張琳娜,趙鳳群

（1.陜西國防工業職業技術學院，陜西戶縣,710300;2.西安理工大學，陜西西安,710032）

基于偏微分方程圖像修補BSCB模型的應用

張琳娜1,趙鳳群2

（1.陜西國防工業職業技術學院，陜西戶縣,710300;2.西安理工大學，陜西西安,710032）

本文在Matlab7.0的環境下，利用相關隨機初始化方案與BSCB模型的結合，修補小尺度污損圖像，并且指出了該方案修補人工與自然圖像的效果。針對同一幅污損圖像，通過三種初始化方案組合BSCB模型對其進行修補，按照修補結果對相關隨機初始化方案對修補效果與效率進行改善方面產生的優勢進行論證。

偏微分方程；圖像修補；BSCB模型；應用

0 引言

在文藝復興時期出現了圖像修補技術，當時主要是在藝術品修補中進行應用。由于不斷變遷的時代，大部分早期的藝術品都存在著各種程度的損傷與裂痕，人們對翻新一些藝術品主要是利用手工對裂縫進行描繪填補。可是由于需要在原作品上直接進行修補，具有極高的風險，因此負責這項工作的主要是具有豐富館藏經驗的專業人員手工進行。

Bertalmio等人由于得到專業人員手工修補方法的啟發，在2000年提出了BSCB圖像修補模型，同時對他們的研究成果進行了發表，明確指出了圖像修補的概念、預期目標以及應用類型，并且應用了偏微分方程的分析方式。

1 BSCB修補原理

由于BSCB模型的建立基礎是手工修補。在對它的修補原理進行討論之前，Bertalmio等人對藝術館藏人員總結的有關手工修補的原則進行訪問。

1.1 手工修補原則

（1）整體圖片明確了怎樣對圖片中的裂痕進行填補，修補的主要目的就是重新形成圖片的統一性；

（2）污損區A四周的信息區域將要延伸至污損區域之內，實現這一目標主要是依靠延伸至邊緣區域的等照度線；

（3）針對無損區域內部產生的等照度線對不同區域進行區分，填充相應的顏色以便對污損區域的邊緣進行匹配；

（4）最后是細節添加信息，也就是紋理。

Bertalmio等人通過分析專業修補工作人員應用的原則得到啟發，進一步提出了BSCB修補模型。在這個模型之中，同時重復實施步驟(2)和(3)，在污損區域內部逐漸傳播信息，盡量將污損區域進行縮小，達到修補目的。

圖1 信息從邊緣向修補區域擴散Fig.1 Information from edge spread to the repair area

1.2 BSCB基本原理

在BSCB方法中，修補的過程就是一個將擴散作為基礎的過程，它的基本思想是憑借原本的角度將修補區域邊緣進一步延伸至區域內部，也就是沿著邊緣逐漸進行切向擴散。

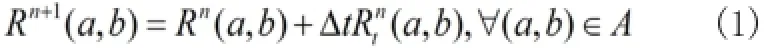
需要特別關注的是，這一迭代過程僅是對存在于修補區域中的像素，對其它區域的像素數值不會進行改變，也就是只修補等待修補區域內的點。伴隨著進行的迭代過程，圖像修補也會獲得更好的效果，下一幅迭代圖像就是憑借對應的更新量對本幅圖像不斷更新的結果。因此，怎樣設計更新量非常關鍵。

按照人工修補的基本原則，需要把等待修補外圍區域A的邊界線延伸到內部，也就是我們要把修補外部的有用信息通過平滑的方式傳送至內部。傳播信息用表示，傳播的方向則是用表示，則有：

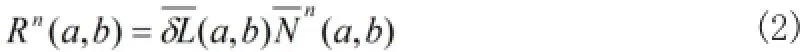
伴隨著逐漸增加的迭代次數，沿著擴散方向傳播量逐漸進入等待修補區域，直到兩次相鄰的修補效果沒有較大差別時結束，這時候.

接下來需要對傳播方向進行確定。在這個模型中，傳播方向選擇等照度線方向。圖像最大灰度變化的方向與梯度相對應，而最小的變化灰度方向則與梯度互相垂直。因此，等照度線方向選擇體現為旋轉90度的梯度方向。在修補中，只需要按照等照度線的方向實施修補就行，梯度旋轉方向是順時針還是逆時針對修補效果不會造成較大影響，只需要確保最小灰度值的變化方向即可。

為了正確演化修補中的圖像，一定在修補中實施擴散。同時為了保證銳利的邊緣，在擴散中利用下式(3)的同性各向非線性擴散方程。

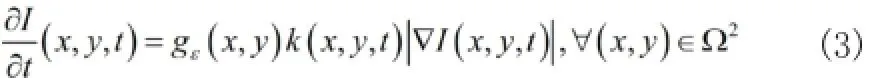
2 BSCB數值離散方案

利用BSCB模型組織計算時，迭代方程為

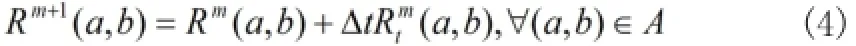
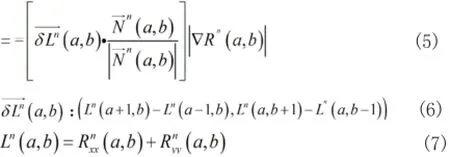
等照度線的單位方向矢量為：

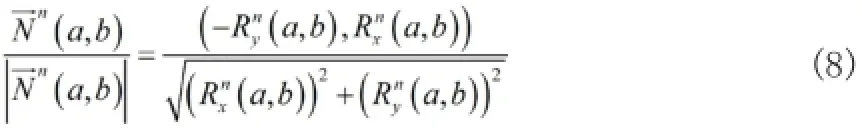
對梯度模值進行計算時，假如直接應用中心差分，極可能出現不穩定的迭代。因此可以應用坡度限制法，定義如下：

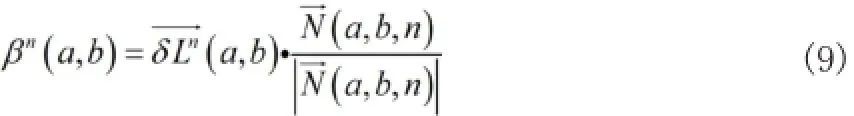
綜合分析，BSCB模型修補圖像的基本步驟：

1)傳播信息的步驟：首先估計一種圖像變化的信息，之后在等照度線方向投影這一變化信息，將投影數值作為內部修補區域的像素更新量。

2)擴散具體步驟：通過各向同性非線性擴散模型的組織擴散。修補過程中，先將步驟1進行一定次數，再將步驟2進行一定次數，反復進行，直到圖像不會出現較大變化為止。

修補圖像就是一個整體迭代過程。每一次迭代是先利用公式實行A次傳播，再利用公式進行B次擴散。迭代總次數主要是由圖像缺損區域大小決定的。

3 改進污損區域的初始化方案

修補圖像過程中，為了順利進行計算，需要賦予等待修補區域內部點的初始數值，也就是初始化污損區域。截止到目前，在修補經典模型中出現了幾種初始化方案。

3.1 初始化純色方案

在BSCB修補模型中出現了初始化純色方案。在這個模型中，研究人員對污損區內的初始化并沒有進行明確。可是他們認為已經損壞了等待修補區域內的信息，修補具體是指周圍信息按照等照度線方向延伸到修補區域內部，見圖3-2。

圖2 初始化純色圖像修補

Fig.2 Initializes a solid color image inpainting

從圖3-2能夠看出，初始修補圖片需要修補區域是全白，伴隨著不斷進行的迭代過程，信息按照等照度線方向逐漸延伸到污損區域，最終實現了修補。

4 實驗結果

本文在Matlab7.0的環境下，利用相關隨機初始化方案與BSCB模型的結合，修補小尺度污損圖像，并且指出了該方案修補人工與自然圖像的效果。針對同一幅污損圖像，通過三種初始化方案組合BSCB模型對其進行修補，按照修補結果對相關隨機初始化方案對修補效果與效率進行改善方面產生的優勢進行論證。

1)人工圖像進行修補

圖4 有關隨機初始化方案的人工圖像修補Fig.4 Random initialization, artificial images fix

2)自然圖像進行修補

圖5 有關隨機初始化方案的自然圖像修補Fig.5 Random initialization scheme natural image patch

從圖4和圖5可以看出，圖像尺度比較小的污損可以獲得較為自然的修補結果；在某些區域能夠看到較為模糊的痕跡。

修補結構模型應當遵守以下方式：當對小尺度的一般污損圖像進行修補時，可以直接應用修補模型積極修補；當對大尺度的污損圖像進行修補時，需要把圖像劃分為結構與紋理內容，針對結構圖像應用結構修補方法進行，紋理圖像則需要應用合成紋理方法。

本文分析了最早把偏微分方程引入到圖像修補BSCB模型，同時從基本原理、離散化方案等方面實施了有效分析。接著指出了BSCB與CDD算法在初始化過程中產生的不足，提出了相關隨機初始化方案。進而得出了實驗結果，從修補結果與效率分析，相關隨機初始化方案產生了顯著的優勢，可以將其與其它擴散方程共同應用，可以獲得良好的修補效果。

[1] Bertalmio M.,Sapiro G.,Caselles V.,Ballester C. Image inpainting[M],in Proceedings of SIGGRAPH 2000,New Orleans,LA,2000.

[2] Chan T F,Shen J H.Non-texture inpainting by curvature-driven diffusions[J].Journal of Visual Communication and Image Representation.2001, 12(4):436-449.

[3] 岡薩里斯.數字圖像處理[M].2 版.北京電子工業出版社, 2003.

[4] 廉曉莉.一種新的基于偏微分方程的圖像修復[J].計算機學報.2009.3

[5] 張帆.基于偏微分方程與邊緣檢測的圖像去噪算法[J].計算機工程與設計.2014.6

張琳娜，女,陜西富平人，（1981— ），碩士，講師， 陜西國防工業職業技術學院,主要從事高等數學研究工作

趙鳳群，女，教授，西安理工大學理學院數學系，主要從事計算數學研究工作。

The application of partial differential equations of image inpainting based on BSCB model

Zhang Linna1,Zhao Fengqun2
(1.Shaanxi Vocational and Technical College of National Defense Industry,Huxian,Shaanxi,710300,China 2.Xian University of Technology,Xi’an,Shaanxi,710048,China)

In this paper,in Matlab7.0 environment,using a combination of correlated random initialization scheme with BSCB model,the repair of small scale defaced image,and pointed out that the scheme of repair of artificial and natural image effect.In accordance with an defaced image,through its three initialization scheme combined BSCB model repair,in accordance with the repair results on related random initialization schemes on the repair effect and efficiency of improving the advantage

Partial differential equation;Image inpainting;BSCB model;Application