三角形課程難度的定量分析比較

陳丹媛　張磊

摘 要： “三角形”是最基本的幾何圖形，在我國初中數學課程體系中有著非常重要的作用.2011年的《全日制義務教育數學課程標準（實驗稿）》與2000年的《全日制九年義務教育初中數學教學大綱（試用修訂版）》中對三角形的教學要求相比，發生了很大的變化.本文利用課程難度定量模型N=αG/T+（1-α）S/T，對我國初中階段“三角形”的課程難度進行定量分析和比較，總結出一些值得廣大數學教師共同關注的變化與調整.

關鍵詞： 三角形 課程難度 可比深度 可比廣度 課程時間

一、問題的提出

2011年的《全日制義務教育數學課程標準（實驗稿）》[1]（以下簡稱《標準》）與2000年的《全日制九年義務教育初中數學教學大綱（試用修訂版）》[2]（以下簡稱《大綱》）中的幾何內容相比，發生了較大的變化.這些變化對初中數學教師理解和實施《標準》提出了挑戰.與《大綱》相比，《標準》中的幾何內容難度有何變化？本文利用刻畫課程難度的數學模型，對《標準》與《大綱》中三角形的難度進行定量分析和比較，探討幾何課程難度變化給學生發散思維能力和推理能力發展帶來的影響.

二、課程難度模型的注釋

據東北師范大學史寧教授對課程難度的研究方法，他們對概念的界定是[3，4]：影響課程難度的基本要素至少有三個：課程深度、課程廣度和課程實施時間.其中，課程深度是指課程內容所需要的思維的深度，可以用課程口標要求的不同程度來量化；課程廣度是指課程內容涉及的范圍和領域的廣泛程度，可以用知識點的數量來量化；課程實施時間是指完成課程內容所需要的時間，可以用“課時”來量化.也就是說，課程難度可以看成是關于課程廣度、課程深度、課程實施時間的一個函數，其中任何一個量的變化均會引起函數值，即課程難度的變化.

顯然，課程難度與課程深度、課程廣度成正比，與課程實施時間成反比.因此，可以用單位課時下課程的廣度和課程的深度衡量課程難度，前者被稱為課程的“可比廣度”，后者被稱為課程的“可比深度”.這樣，課程的可比廣度與可比深度越大，這門課程越難.但有一個側重程度，即需要考慮課程的可比廣度和課程的可比深度哪個對課程難度的影響大.因此，課程難度可以看成是“可比廣度”和“可比深度”的加權平均值.

如果用N表示課程難度，用S表示課程深度，用G表示課程廣度，用T表示課程時間，綜上所述，可以建立刻畫數學課程難度的模型如下：

N=αG/T+（1-α）S/T（1）

其中G/T表示可比廣度，S/T表示可比深度，α稱為加權系數，0<α<1，是一個經驗性常數，反映了可比廣度、可比深度對課程難度影響的側重程度.

三、《標準》與《大綱》中三角形的難度量化比較

（一）課程時間

對于《標準》，在“人教版”[5]中：八年級上冊第11章“三角形”中出現“與三角形有關的線段”、“與三角形有關的角”是6課時，第12章“全等三角形”是11課時，第13章“軸對稱”中出現“等腰三角形”是5課時；八年級下冊在第17章“勾股定理”是9課時；九年級下冊在第27章“相似”中出現“相似三角形”是7課時，第28章“銳角三角函數”中是12課時，共計50課時，于是T■=50.

而在《大綱》下的教科書中安排45課時，于是，T■=45.

（二）課程廣度

《標準》中三角形的知識點分布較散，相應課程內容的知識點合計41個，取綜合的課程廣度系數G■=41.考慮到“圖形與變換”在《大綱》中出現在《三角形》之中，并且僅出現軸對稱，相應課程內容的知識點合計39個（不含選學內容“反證法”），取綜合的課程廣度系數為G■=39.

（三）課程深度

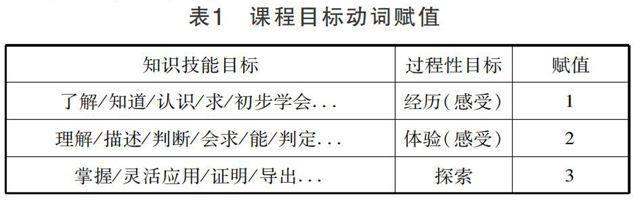
《大綱》中是按四個層次“了解”“理解”“靈活應用”陳述目標（要求）的，《標準》中則是按三個層次陳述目標（要求）的。考慮到“掌握”這一要求與“靈活應用”區別并不是很大，為了與《標準》中的層次對應，將“掌握”與“靈活應用”合并為同一個層次，則對《大綱》和《標準》中過程性目標賦值如表1.

表1 課程目標動詞賦值

（四）課程內容要求的對比

1.《標準》中“三角形”相應課程內容的知識點對應的課程深度值分別如下。

（1）概念部分

三角形（包括三角形頂點、邊、內角、外角、角平分線、中線和高）：2；全等三角形：2；等腰三角形：1；直角三角形：1；三角形重心：l；三角形的內心、外心：1；相似三角形：1；銳角三角函數：2.

（2）定理部分

三角形的穩定性：1；三角形內角和定理：3；三角形的邊長關系：3；三角形外角和定理：3；三角形中位線定理：3；三角形全等判定SAS：3；三角形全等判定ASA：3；三角形全等判定AAS：3；三角形全等判定SSS：3；等腰三角形性質定理：3；等腰三角形判定定理：3；三線合一定理：3；等邊三角形性質定理：3；等邊三角形判定定理：3；直角三角形的性質定理：3；直角三角形全等判定：3；勾股定理：3；勾股定理的逆定理：3；三角形的中位線定理：3；三角形相似的判定定理：1；三角形相似的性質定理：1.

（3）技能部分

作三角形的角平分線、中線和高：2；作等腰三角形的對稱軸：2；三邊作三角形：2；兩邊及其夾角作三角形：2；兩角及其夾邊作三角形：2；底邊及底邊上的高作等腰三角形：2；一直角邊及斜邊作直角三角形：2；30°，45°，60°的三角函數：l；解三角形：2；用計算器求銳角三角形函數值：2；求三角形函數值對應的銳角：2；作三角形的內切圓：2.

2.《大綱》中“三角形”相應課程內容的知識點對應的課程深度值分別如下。

（1）概念部分

三角形（包括三角形頂點、邊、內角、外角、角平分線、中線和高）：1；全等三角形：l；三角形的內心、外心：1；相似三角形：2；相似比：2；銳角三角函數：1.

（2）定理部分

三角形的穩定性：1；三角形內角和定理：3；三角形的邊長關系：2；三角形外角和定理：3；三角形中位線定理：3；三角形全等判定SAS：3；三角形全等判定ASA：3；三角形全等判定AAS：3；三角形全等判定SSS：3；等腰三角形性質定理：3；等腰三角形判定定理：3；三線合一定理：3；等邊三角形性質定理：3；等邊三角形判定定理：3；直角三角形的性質定理：3；直角三角形全等判定：2；勾股定理：3；勾股定理的逆定理：2；三角形的中位線定理：3；三角形相似的判定定理：3；三角形相似的性質定理：2.

（3）技能部分

作三角形的角平分線、中線和高：2；作等腰三角形的對稱軸：2；三邊作三角形：2；兩邊及其夾角作三角形：2；兩角及其夾邊作三角形：2；底邊及底邊上的高作等腰三角形：2；一直角邊及斜邊作直角三角形：2；30°，45°，60°的三角函數：l；解三角形：2；用計算器求銳角三角形函數值：2；求三角形函數值對應的銳角：2；作三角形的內切圓：2.

3.與《大綱》相比，《標準》中“三角形”課程內容要求的變化。

（1）概念部分

對“三角形（包括三角形頂點、邊、內角、外角、角平分線，中線和高）、全等三角形、銳角三角函數”三個內容的難度要求從了解提高到理解，而對“相似三角形”，則從理解降低到了解；增加“等腰三角形、直角三角形、三角形重心”三個內容，并要求理解；刪除原本要求理解的“相似比”.

（2）定理部分

對“三角形的邊長關系、直角三角形全等判定、勾股定理的逆定理”三個內容的難度要求，從理解提高到掌握，而對“三角形相似的判定定理”、“三角形相似的性質定理”，則分別從靈活運用、理解降低到了解.

（3）技能部分

分別增加會作“作三角形的外接圓”，刪除原本要求會作“作三角形的角平分線、中線和高”的技能要求.

（五）難度比較

根據以上數據，分別求出《標準》與《大綱》中三角形部分的可比廣度、可比深度[6]，統計數據及比較結果如表2所示：

表2 《標準》與《大綱》中三角形部分的數據統計結果

注：右上角的數字分別代表與《大綱》中三角形相比，《標準》中三角形的可比廣度與可比深度的變化，用“+”代表增加，用“-”代表降低.

1.根據所建立的數學模型N=αG/T+（1-α）S/T，分別表示出《標準》與《大綱》中三角形部分的課程難度：

四、結論

從以上統計數據可以看出，課程實施時間、課程廣度、課程深度三個量當中的任何一個有微小變化，都會引起課程難度的變化.分析上述表格的數據，可以發現，《標準》下的《大綱》下的《大綱》下的《三角形》內容基本一致.《標準》下的《三角形》課程難度有所降低，主要原因是《標準》中該部分內容的課程廣度和課程深度增加不大，但課程實施時間增加較大，使其可比廣度和可比深度分別降低了0.05和0.14.也就是說如果時間充足的話，可比廣度和可比深度也會有所降低.

這啟示我們，如果課程實施時間較長，課程難度就會大大降低.也就是說，時間允許的話，完成《標準》中很多的探索對學生更好地掌握知識有很大的幫助，從而培養學生的發散思維能力和推理能力.

參考文獻：

[1]中華人民共和國教育部.全日制義務教育數學課程標準（實驗稿）[M].北京：人民教育出版社，2011.

[2]中華人民共和國教育部.全日制九年義務教育初中數學教學大綱（試用修訂版）[M].北京：人民教育出版社，2000.

[3]呂世虎，史寧中，陳婷.《標準》與《大綱》中幾何部分內容難度的比較研究[J].課程·教材·教法，2006（8）：38-43.

[4]史寧中，孔凡哲，李淑文.課程難度模型：我國義務教育幾何課程難度的對比[J].東北師人學報（哲學社會科學版），2005（6）：151-155.

[5]課程教材研究所.義務教育教科書.[M].北京：人民教育出版社，2013.

[6]李高峰.課程難度模型運用中的偏差及其修正—與史寧中教授等商榷[J].上海教育科研，2010.3：46-49.

基金項目：2014年廣東省大學生創新創業訓練計劃項目：基于課程難度定量分析模型下的初中幾何課程難度研究，項目編號：201410578047。