進港航道中船舶擱淺概率的蒙特卡洛仿真

任亞磊，牟軍敏，李亞軍，易 侃

（1內河航運技術湖北省重點實驗室（武漢理工大學），武漢 430063；2中華人民共和國上海海事局，上海 200086 3高性能船舶技術教育部重點實驗室（武漢理工大學），武漢 430063）

進港航道中船舶擱淺概率的蒙特卡洛仿真

任亞磊1，2，牟軍敏3，李亞軍1，易 侃1

（1內河航運技術湖北省重點實驗室（武漢理工大學），武漢 430063；2中華人民共和國上海海事局，上海 200086 3高性能船舶技術教育部重點實驗室（武漢理工大學），武漢 430063）

文章通過對影響船舶吃水的主要因素，如船舶對波浪的響應、橫傾引起的吃水變化、淺水中船舶的下坐以及航道底部等的分布規律的研究，擬合出其概率密度函數，然后使用蒙特卡洛（Monte Carlo）仿真船舶擱淺概率，其中船舶對波浪的響應采用了先進的粘性流數值計算方法。該模型可為受限水域航道建設和船舶安全通航提供參考。

蒙特卡洛；動態吃水；船舶擱淺概率

1 引 言

隨著船舶的大型化和高速化，船舶擱淺的問題日益凸顯。擱淺事故常帶來船體結構損壞、環境污染甚至人員傷亡等嚴重后果，自上世紀50年代末以來國內外學者對其進行了一系列研究。祁恩榮[1]對前人的成果進行了總結，這些研究成果大概可歸納為三類：第一類主要從船舶實際操作入手開展研究，如采用實船事故調查、事件樹、模糊事件樹、決策樹、貝葉斯網絡等方法，探索擱淺的原因和機理，對船

舶偏離航道、機械失效、救援失效、惡劣海況等導致擱淺的因素進行分析，定性或定量地描述船舶擱淺風險的大小[2-5]；第二類主要從船體結構力學入手研究，采用縮尺或實尺度模型試驗、有限元分析、簡化數值模擬和解析經驗公式等方法，研究擱淺事故中船舶力學問題，分析船底結構損傷、變形受力，為改善船體結構提供參考[6-7]；第三類則側重于航道中船舶通航條件等相關數據的采集和分析，以充分利用航道水深，減小船舶擱淺風險。黃蘊和[8]針對重載船舶在進出浙江海門港乘潮作業問題，結合港外航道潮汐變化規律，研討了現有航道水深條件下乘潮作業的合理性。胡勤友[9]綜合潮汐數據、電子海圖、船位和航向信息等開發了船用擱淺預警系統。

擱淺是個非常復雜的科學與工程技術問題，但其發生的必要條件比較簡單，即航行水域水深相對船舶吃水不足。如大型船舶駛離設計航道導致擱淺，或在動靜力作用下船舶浮態發生變化，導致在航道中吃水不足擱淺。考慮到上述文獻中對動態吃水引起可航水深不足的研究相對偏少，本文主要圍繞船舶動態吃水開展船舶擱淺概率的研究。總體上，影響船舶動態吃水的主要因素包括：潮汐、船舶對波浪的響應、淺水中船舶下坐、船舶操縱運動所致浮態變化以及航道底部情況等。

這些因素具有很強的隨機性和不確定性。結合船舶水動力計算與航道工程技術，綜合考慮以上各因素，已是目前擱淺概率研究的新方法。澳大利亞的O’Brien[10]博士創造了動態富裕水深系統（Dynamic Under-keel Clearance System）并開發了系列的產品，注冊了DUKC的商標和專利。相比較傳統的港口航道規劃設計方法和建設使用過程中地毯式疏浚技術，這種應用系統融合了船舶波浪中運動響應、概率設計、氣象預報及海洋水文等多要素信息，可以計算出一定置信度下船舶靠離港的最小安全富裕水深值和乘潮時間窗，充分利用了水深，減少了港口疏浚費用。另外一種較新的方法是蒙特卡洛（Monte Carlo）仿真。它在考慮影響船舶吃水各因素的基礎上，根據其分布規律產生大量隨機數，最后統計得到擱淺的頻率，進而得出概率。Schoenmakers[11]采用該方法對開普敦港（Cape Town）進港航道的設計深度進行了驗算，波浪處理采用了swan模型，船舶對波浪的響應采用了簡化的經驗公式，而且沒有考慮船舶在波浪中的橫傾和縱傾問題。Gucma[12]采用了類似的方法，更偏向于經驗型，相關數據的獲取采用了模擬器與實船實驗相結合的方法，另外又考慮了可航的泥底、各種測量誤差等因素，求出擱淺的概率。但受限于試驗次數和實驗條件的設置，誤差等參數選取進行了大量簡化。為此，本文根據蒙特卡洛仿真的思想，結合CFD計算結果，開展了設計代表船舶在航道中擱淺的概率計算，并以浙江省臺州某港區航道進行了實例研究。

2 基本原理和方法

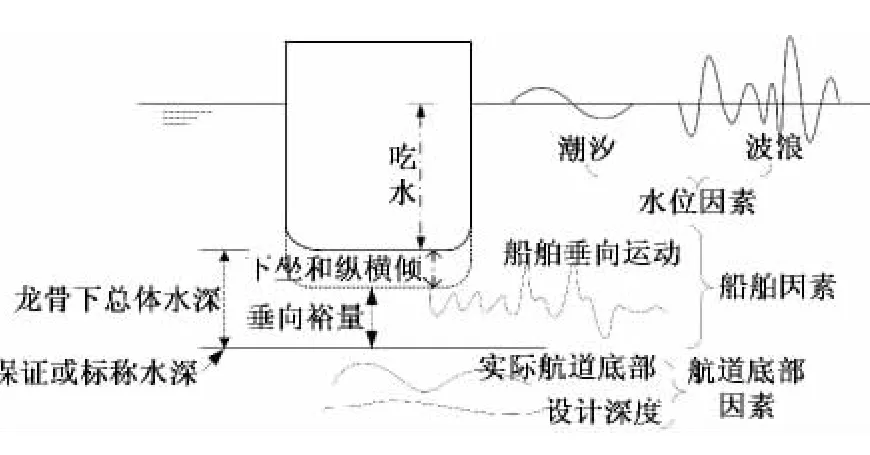
圖1 導致船舶吃水變化的因素Fig.1 Causations to ship dynamic draft

蒙特卡洛方法，又稱計算機隨機模擬方法，是一種基于“隨機數”的計算方法。該方法的基本思想就是用事件發生的“頻率”來決定事件的“概率”。上世紀40年代電子計算機的出現，特別是近年來高速電子計算機的出現，使得人們可以在計算機上利用數學方法大量、快速地產生一定統計特征的隨機數進行模擬試驗。目前這一方法已經廣泛地運用到數學、物理、管理、生物遺傳、社會科學等領域，并顯示出了特殊的優越性。

實際應用中的隨機數通常都是某些數學公式計算而產生的偽隨機數，這些數不是嚴格意義上的隨機數，但是，只要它們能夠通過隨機數的一系列統計檢驗，就可以將其作為真隨機數使用。因此，理論上要求偽隨機數產生器具備以下特征：良好的統計分布特性，高效率的偽隨機數產生，偽隨機數產生的循環周期長，偽隨機數可以重復產生等。這些偽隨機數產生器借助MATLAB等數學工具軟件可以方便實現。船舶在航道中運動，引起吃水變化是高度復雜的過程，涉及了多種因素作用，如圖1所示。

船舶所需吃水與航道水深的關系可以用（1）式表示：

其中：d 為航道深度（m）；Htide為潮高（m）；D 為設計船型吃水（m）；r為船舶對波浪的垂向響應（m）；Bf為航道底部情況（m）；h 為橫傾引起的吃水變化（m）；s為淺水引起的下坐（squat）（m）。

從隨機過程理論看，上式中許多因子是隨機的，而且符合某種統計分布特征。因此根據蒙特卡洛方法求取船舶擱淺概率，即P（Z<0），可以通過研究上式中各因素的概率密度函數，產生大量的隨機數序列，最后統計船舶擱淺的頻率以代替擱淺概率。

值得一提的是，對于同一航道，不同的航段航行條件也有較大差異，如防波堤內外航道的風浪要素、以及航段曲率等。因此，為方便研究可根據不同的航行條件將航道劃分為數段，分別進行研究。

3 相關參數求取

3.1 航道深度

對航道設計來說，航道深度是最終求取的目標。通常按照港口航道設計要求的擱淺率為臨界點，或者遵循費效平衡的原則確定。

當然對于一定設計深度的航道，本文方法則可以計算出代表船型的擱淺概率，為船舶安全通航提供參考。

3.2 潮汐

潮汐因地而異，較復雜，但有其規律，可進行準確預報。合理利用潮汐，根據潮汐預報制作出船舶安全通過航道的時間表，可有效提高航道通過能力，減少疏浚工作量，節約成本。具體潮高可通過潮汐表求得。如果精確計算，應考慮統計船舶通過過程中潮汐變化；在實際操作中，若船舶通過某一航段所需時間較短，潮高變化不大，也可簡化為采用此時間段內的平均潮高。

3.3 設計船型吃水

船舶吃水一般是指船舶的吃水深度，即船舶的底部至船體與水面相連處的垂直距離。船舶吃水有設計吃水和結構吃水兩種，設計吃水是指船舶裝載設計載重量貨物情況下達到的吃水深度；結構吃水是船舶裝載最大載重量貨物情況下達到的吃水深度。這里取設計吃水作為檢驗值。

3.4 船舶對波浪的響應

船舶對波浪的響應是對波浪條件的統計響應，這里既有波浪要素的統計規律，又有船舶響應的統計規律。本文所述的船舶對波浪響應是對某種特定波浪條件的響應，即根據波浪要素的統計資料，采用設計波法描述工程水域的不規則波浪，亦即選取工程水域的不規則波特征要素構造規則波，以特定波浪條件來代替實際波，簡化計算。

船舶在波浪中的運動與海域水深、潮位、波浪要素及船體自身的尺度和型線等直接相關。目前，實際海域中海洋結構物的波浪載荷及運動的研究方法主要有設計波法、設計譜法和時域計算方法等。將來隨著仿真技術的進步，使用模擬器與實船實驗相結合的方法獲取數據將成為主流，不過現階段受限于試驗次數和實驗條件，各參數選取都進行了大量簡化，結果較粗糙，因此最終還是選用了CFD方法計算構造波中的船舶響應。

由于Boussinesq方程計算模型通常是將三維問題簡化為平面二維問題進行計算[13]，本文采用粘性流數值計算方法，用體積分數VOF法跟蹤自由面波形，計算船體在波浪中的粘性流場，得到船體受到的波浪力和船體的在波浪中的運動響應。計算船舶對波浪的響應的具體方法是[14]：

（1）采用設計波法描述工程水域的不規則波浪，即選取工程水域的不規則波特征要素，構造規則波。如選取若干年一遇為特征波重現期，分別選取其中十分之一波高H1/10和有義波高H1/3及其周期作為設計波的波高和周期，構造三階Stokes規則波。

（2）選取代表船型船體周圍水域為計算流體域，考慮水的粘性影響，通過邊界造波法，求解粘性非定常Navier-Stokes（N-S）方程，再計算流體域生成三階Stokes波，計算波浪中船體周圍流場和船體受到的水動力。然后根據船體運動方程，得到船體在波浪中的六自由度運動。

3.5 航道底部情況

由于沖刷、淤積和施工工藝的不確定因素，航道底部不均勻等高。一般可以通過實際測量，擬合出其分布函數。

3.6 橫傾引起的吃水變化

橫傾是指船舶自正浮狀態向左舷或右舷方向傾斜的一種浮態，此處僅考慮由于船舶轉向操作引起的橫傾，波浪引起的橫傾的計算，在3.4節中已有介紹。船舶橫傾導致吃水變化如圖2所示，圖中：C為船舶重心；α為橫傾角；h為吃水變化。由此不難推出h的計算公式：

3.7 淺水引起的下坐（Squat）

船體在淺水中航行下坐，主要包括船體整體下沉和縱傾變化兩部分。1967年Tuck利用細長體理論首先給出了一種估算方法。之后，在此基礎上出現了許多解析式或半經驗的計算公式[15]，如：Hooft公 式 （1974）、Huuska 公 式 （1976）、Eryuzlu 公 式（1978）、Barrass 公式 （1981）、Romisch 公式（1989）、Millward公式 （1990）、Millward 公式（1992）、Eryuzlu公式（1994）和 Ankudinov 公式（1996）。 但實際上，即使對同一種船型，用不同的公式計算差別仍然會較大，特別是在船速大于8節后，差別更為顯著。因此，理論上任何一種船舶航行下沉量的計算方法都需要大量的實船測量數據進行驗證和修正。如Gucma[12]采用GPS-RTK實驗給多種模型賦權重值確定下坐。當然，在實測資料相對匱乏的情況下，實際計算可以根據各公式的應用范圍、船型特點、航道特點以及通航密度等條件進行合理選取。而且從安全角度考慮，不妨采用下沉量較大值者。

一般來說航道中船舶的下坐可以采用BarassⅡ公式

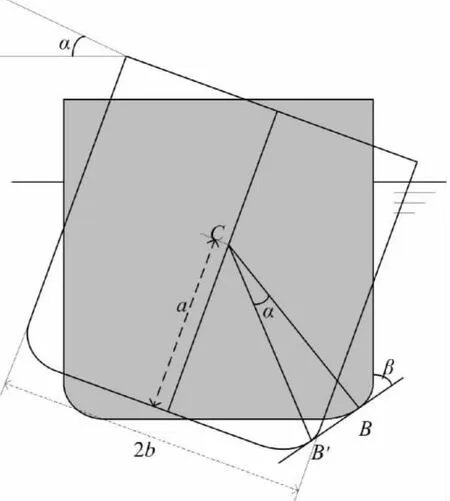
圖2 船舶橫傾導致吃水變化示意圖Fig.2 Ship heel and draft change

其中：Smax為由于淺水下坐導致的吃水變化（m）；Cb為船舶方形系數。

上式中：AS-vertical為船體橫切面面積（m2），Ach為航道橫切面面積（m2），VK為船舶的對地航速（kn）。

4 實例研究

4.1 工程概況

臺州灣位于浙江中部沿海，為開敞的河口灣。海岸屬于淤泥質或人工海岸，以平直的淤漲型岸灘為主。海灣面積為911.561 km2，其中潮灘面積258.748 km2，淺水區面積比例相對較高。隨著海洋產業的發展，特別是世界級煉油和化工一體化工廠選址臺州灣黃礁作業區，作業區港口航道遠景規劃5萬噸級雙向乘潮通航，全長12 km，底寬260 m，設計底標高-11.5 m。

4.2 數據處理

為方便研究根據航速、航道曲率、波浪大小等因素將航道劃分為九段分別進行研究，如圖3所示。

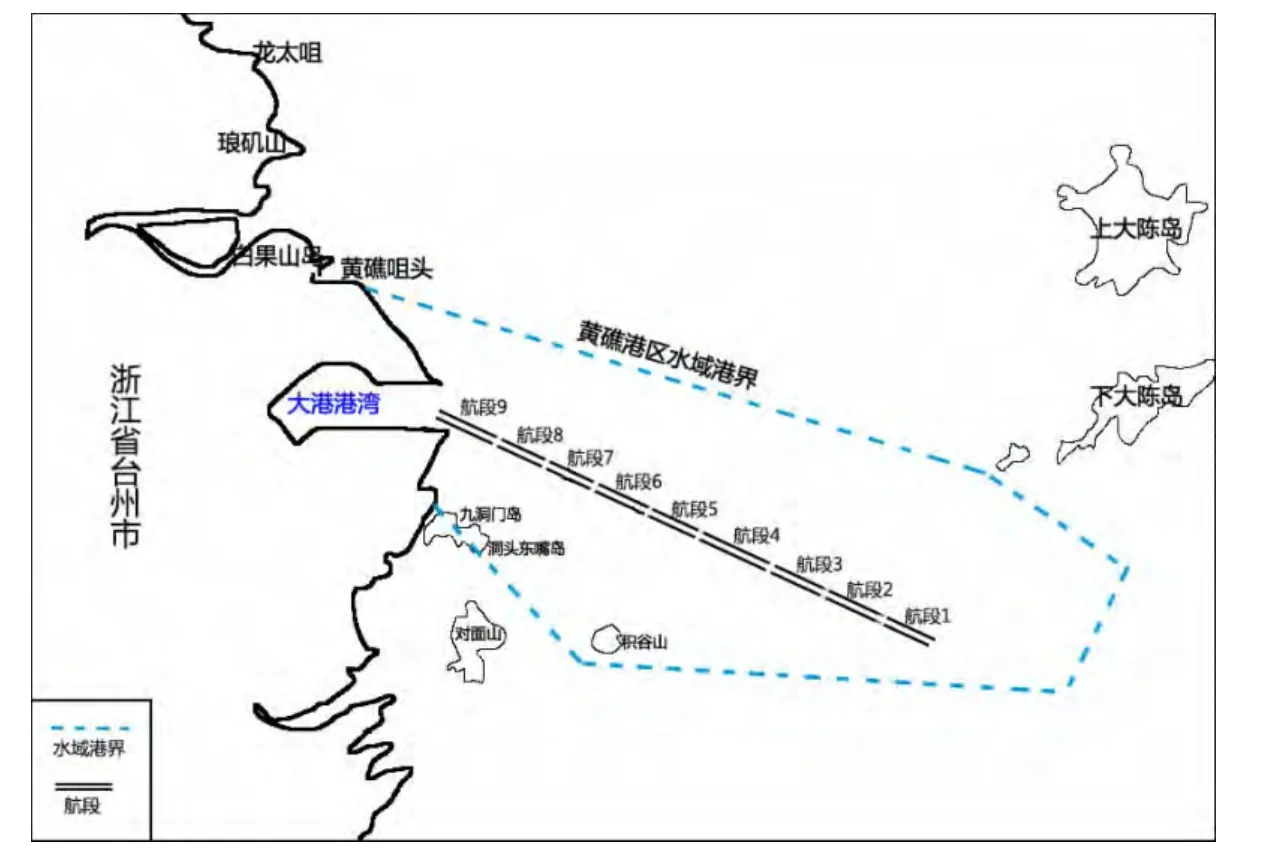
圖3 航段劃分示意圖Fig.3 Sections divided for the approach channel

4.2.1 航道深度

航道遠景規劃5萬噸級雙向乘潮通航，全長12 km，底寬260 m，設計底標高-11.5 m。

4.2.2 潮汐

本海域無長期實測驗潮資料，國家海洋局上海東海海洋勘測設計研究院在其南部松門鎮橫門設立潮位站，進行了一年的潮位觀測（2008.10～2009.9）。根據實測驗潮資料統計、計算得出本海域潮位特征值見表1。

表1 橫門站潮位特征值Tab.1 Characteristics of tide level(Heng-men hydrographic station)

船舶通過航道時的具體潮高及其分布變化可通過潮汐表求得，本文是求取設計航道高水位時5萬噸級油船擱淺概率，因此選取工程設計乘潮高水位5.33 m為典型水位進行簡化計算，為提高仿真精度，應考慮潮高大于5.33 m時的潮汐水位變化分布，作為一個變量加到設計乘潮高水位上。

4.2.3設計船型吃水

所研究航道內行駛的主要運輸船型是以1～3萬噸級的成品油船為主，最大船型可達5萬噸級。模型所選取標準船型主尺度如表2所示。

表2 標準船型主尺度Tab.2 Pariticulars of the designed ship

4.2.4 船舶對波浪的響應

本文選取的是波向頻率最高的NE～ENE，以2年一遇為特征波重現期，以其H1/10作為設計波的波高和周期，構造三階Stokes規則波。迎浪和橫浪是船舶航行的兩個極端條件，尤其是橫浪對船體縱向和橫向的浮態影響最大，本文計算了船舶迎浪和橫浪下的縱搖、垂蕩和橫搖運動。波浪要素選取H1/10，即H=3.6 m，T=10 s，水深為h=16.83 m，船舶航速V=5 kns。計算結果如圖4、5所示。

圖4 迎浪船體垂蕩、橫搖及縱搖運動時歷Fig.4 Ship response to head sea in time domain(heave,roll and pitch)

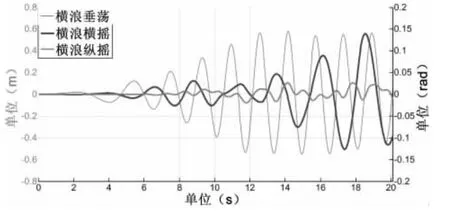
圖5 橫浪船體垂蕩、橫搖及縱搖運動時歷Fig.5 Ship response to transverse sea in time domain(heave,roll and pitch)

4.2.5 航道底部情況

航道底部情況由于施工精度、沖刷、淤積等隨機、不確定因素的影響，精確地描述非常困難。對于臺州航道，通過測量，采用均值為0.1，標準差為0.1的正態分布近似描述。

4.2.6 橫傾引起的吃水變化

此處只考慮船舶轉向操作引起的橫傾，該值大小與船型、船速、所操舵角、重心高度、初穩心高度等因素密切相關，實際觀測表明其最大值一般不超過5°。Schoenmakers[11]認為船舶在彎曲航段，因操舵引起的橫傾值一般不超過5°，具體的處理方法是通過航行仿真，選取每一航段的最大橫傾值，數據選取從2.5°到5°不等；Gucma[12]則選取+/-3°簡化處理。考慮到文獻[11]中研究船型為集裝箱船、文獻[12]中研究船型為客船，而本文的研究對象為油輪，穩性大于集裝箱船和客船，又結合幾位船長的意見，最終選取操縱橫傾為2°。

4.2.7 淺水引起的下坐（Squat）

根據BarassⅡ公式，求取下坐值關鍵在于獲取船舶的方型系數和船速。所選取標準船型的方型系數參照表2，船速由各航段實測得出，取其平均速度，并以一定的分布規律進行描述，如航段1平均船速符合威布爾分布η=2.04，β=1.93；航段9符合均值為6.03，標準差為1.81的正態分布。

4.3 計算結果

分別以航段1（防波堤外直航道）和航段9（防波堤內彎曲航道）為代表進行計算，結果分別如圖6至9所示。

從仿真結果看，10萬次的仿真中，5萬噸油船在航段1橫浪條件下擱淺次數為49次，迎浪條件下為1次，航段9橫浪和迎浪條件下都沒有發生擱淺。結果表明，航道設計乘潮高水位16.83 m，具有較高的可靠性，可以滿足設計船型在一般條件下的安全航行，且具有較大的安全裕量。如果以港口管理部門所能接受的擱淺率0.5%為臨界點，則航段1的安全裕量為0.47 m，即航道設計深度為11.03 m即能滿足設計要求。以5萬噸油船每厘米吃水噸數65噸計算，現有航道水深可提升運力3 055噸。航段9的安全裕量為1.29 m，即航道設計深度為10.21 m即能滿足設計要求。以5萬噸油船每厘米吃水噸數65噸計算，現有航道水深可提升運力8 385噸。就航道疏浚而言，上述方法節省的疏浚量非常可觀，經濟效益明顯。

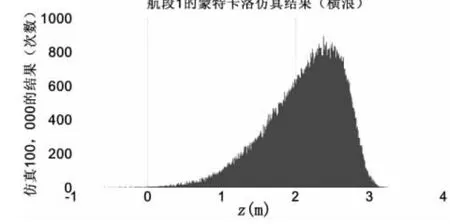
圖6 航段1橫浪5萬噸級滿載油船擱淺概率仿真Fig.6 Probability Simulating for a 50 000 ton class laden oil tanker grounding in Section 1(transverse sea)

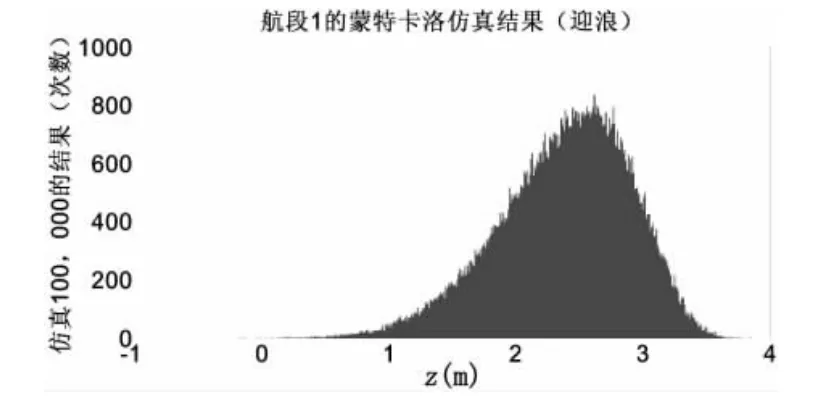
圖7 航段1迎浪5萬噸級滿載油船擱淺概率仿真Fig.Probability Simulating for a 50 000 ton class laden oil tanker grounding in Section 1(head sea)

圖8 航段9橫浪5萬噸級滿載油船擱淺概率仿真Fig.8 Probability Simulating for a 50 000 ton class laden oil tanker grounding in Section 9(transverse sea)

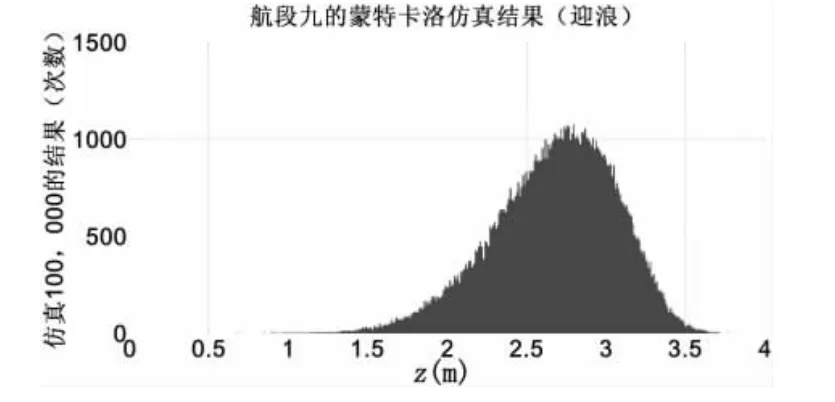
圖9 航段9迎浪5萬噸級滿載油船擱淺概率仿真Fig.9 Probability Simulating for a 50 000 ton class laden oil tanker grounding in Section 9(head sea)

5 結 論

從隨機過程的角度考慮影響船舶吃水的主要因素：船舶對波浪的響應、橫傾引起的吃水變化、淺水中船舶的下坐以及航道底部情況的分布規律，開展船舶擱淺概率的蒙特卡洛仿真，相對于傳統基于規范的設計和分析方法，有其明顯的優點。

本文在綜合考慮水動力計算和航道工程技術的基礎上，針對浙江臺州某港區的設計航道水深進行了蒙特卡洛實例仿真，結果表明原規劃航道設計水深還有較大的裕度。

[1]祁恩榮,崔維成.船舶碰撞和擱淺研究綜述[J].船舶力學,2001,5(4):67-80.Qi Enrong,Cui Weicheng.A state-of-the-art review on ship collision and grounding[J].Journal of Ship Mechanics,2001,5(4):67-80.

[2]陳 剛,張圣坤.船舶擱淺概率的模糊事件樹分析[J].上海交通大學學報,2002,36(1):112-116.

[3]于 鵬.擱淺船舶危險度定量研究[D].大連:大連海事大學,2011.

[4]Zhu Renqing,Zhao Hongjiang.Probability of ship grounding and collision calculation[J].Shipbuilding Science and Technology,1999(1):4-9.

[5]胡中凱,尹 群,劉海燕等.基于貝葉斯網絡方法對船舶擱淺概率的研究[J].艦船科學技術,2010,32(2):23-26.

[6]劉 峰,王自力,崔維成.船舶結構的擱淺數值仿真研究[J].船舶,2006,3:24-27.

[7]楊傳武,王安穩.小水線面船擱淺過程的數值仿真研究[J].固體力學學報,2006,29:24-27.

[8]黃蘊和,金丕信.海門港外航道通航條件研究[J].中國航海,1996,1:77-83.

[9]龔安祥,胡勤友,徐 鐵.SAGA:一種新的船舶擱淺預警模型[J].大連海事大學學報,2007,28(1):106-110.

[10]O’Brien T.Experience using an innovative under keel clearance prediction system in australian ports[J].Port Tech.Int.,1999(6):165-169.

[11]Schoenmakers N W A,WIT A B F de.Probabilistic design entrance channel port of cape town[R].Minor thesis.Hydraulic Engineering,2006.

[12]Gucma L,Marta S.Monte Carlo method of ship’s under-keel clearance evaluation for safety of ferry approaching to Ystad port determination[J].Journal of Konbin,2008,5(8):36-44.

[13]王大國,鄒志利,唐春安.港口非線性波浪耦合計算模型研究[J].力學學報,2007(5):587-594.

[14]武漢理工大學航運學院.臺州灣岸線的淺水深用通航安全關鍵技術研究報告[R].浙江交通廳科技項目編號:2009W11,2009.

[15]洪碧光,于 洋.船舶在淺水中航行下沉量的計算方法[J].大連海事大學學報,2003,29(2):1-5.

Monte Carlo simulation for the grounding probability of ship maneuvering in approach channels

REN Ya-lei1，2,MOU Jun-min3,LI Ya-jun1,YI Kan1
(1 Hubei Key Laboratory of Inland Shipping Technology(Wuhan University of Technology),Wuhan 430063,China;2 Shanghai Maritime Safety Administration,Shanghai 200086,China;3 Key Laboratory of High Performance Ship Technology(Wuhan University of Technology),Ministry of Education,Wuhan 430063,China)

In this paper,a deterministic model of ship under keel clearance is presented,which contains a set of random variables caused by ship maneuvering,including the vertical motion induced by wave,the heel during ship turning,the squat in sallow water and hydrographic data of seabed.They are represented by certain distributions,and the ship basic response to typical wave is predicted by a CFD method.Via Monte Carlo simulation,the stochastic uncertainty of a ship under keel clearance is observed,and the grounding probability can support channel construction and vessel traffic safety analysis in restricted waterways.

Monte Carlo;dynamic draft;ship grounding probability

U657.2 U676.1

A

10.3969/j.issn.1007-7294.2014.05.007

1007-7294（2014）05-0532-08

2013-11-23

國家自然科學基金委員會（NSFC）與荷蘭科學研究組織（NWO）合作研究項目（51061130548）

任亞磊（1988-），男，武漢理工大學碩士研究生，E-mail：renyalei1988@163.com；

牟軍敏（1974-），男，博士，武漢理工大學教授。