小型柔性接頭纏裹式防熱套力矩特性數值分析①

王 超，任軍學，郝文強，劉 宇，楊敬賢

(1．北京航空航天大學宇航學院，北京 100191;2．上海新力動力設備研究所，上海 200125)

0 引言

柔性接頭是由增強件、彈性件和前后法蘭4部分組成的固體火箭發動機推力矢量控制的核心部件。其中，增強件和彈性件一般為多層且交替粘接，再通過前后法蘭與噴管的固定部分和擺動部分連接在一起。柔性噴管消除了軸向推力損失和擺動分離線，本身又具有足夠的抗扭剛度，具有致偏能力強、結構簡單、沖質比高、推力損失小等優點，一般用在大型戰略導彈和助推器上［1］。近年來，由于戰術導彈對垂直發射快速轉彎、越肩發射等高機動性能要求的提高，小型柔性接頭已被應用到相關型號上［2－5］，如美國 SM-3和 Terrier LEAP 第三級發動機、歐洲 aster15/30 等［6－9］。

由于柔性接頭會暴露在發動機的熱燃氣環境中，因此對金屬增強件的柔性接頭必須使用防熱套，將其與高溫燃氣隔開［10］，但防熱套的存在，會增大柔性接頭擺動所需的作動力矩。然而，與戰略導彈相比，戰術導彈結構空間尺寸有限，過大的防熱套力矩會增大伺服機構的功率尺寸，給整個導彈的布局帶來困難。另外，戰術導彈一般工作壓強較高，高壓下防熱套的力矩特性對整個柔性接頭的設計意義重大。目前，國內外對防熱套力矩的研究都是基于試驗方法，且以大型接頭波紋式防熱套為主［11］，對小型防熱套力矩特性研究較少。

本文建立某戰術導彈用柔性接頭帶防熱套和不帶防熱套的三維有限元模型，數值模擬不同容壓條件下接頭的擺動過程，并對該接頭進行擺動試驗，測得不同容壓下的防熱套力矩，對比了試驗結果與數值模擬結果，考察了球坐標系下防熱套剖面上的剪應力場分布，研究典型剖面上剪應力場隨容壓的變化規律，研究結果可為小型柔性接頭、防熱套和伺服機構的設計提供參考。

1 柔性接頭及試驗系統

1．1 柔性接頭

圖1為纏裹式防熱套小型柔性接頭的結構示意圖，由增強件、彈性件、前后法蘭和纏裹式防熱套組成，主要結構參數取值如表1所示。增強件及前后法蘭由高比強度的30CrMnSiA材料制造。彈性件和防熱套用硅橡膠材料與文獻［12］相同。

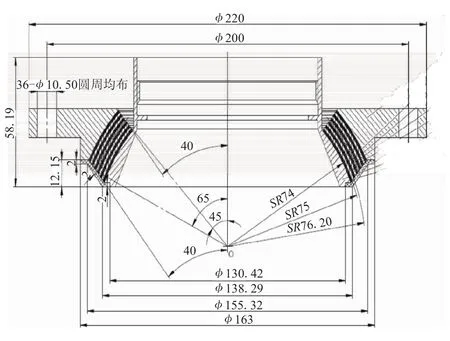
圖1 柔性接頭結構示意圖Fig．1 Sketch of flexible joint

1．2 試驗系統

柔性接頭冷試試驗系統裝置如圖2所示。壓力容器內充填高壓氮氣，模擬燃燒室高壓環境，電動伺服機構提供柔性接頭擺動所需的作動力矩。傾角傳感器和2個水平安裝的位移傳感器都可用于測試柔性接頭擺角，鉛垂安裝的位移傳感器結合2個水平傳感器用于測試柔性接頭的擺心［13］，拉壓力傳感器用于測試伺服機構作動力，由作動力和擺心即可計算出柔性接頭擺動所需的力矩。

表1 柔性接頭結構參數Table 1 Structure parameter of flexible joint

圖2 柔性接頭冷試試驗系統Fig．2 Flexible joint bench test fixture

2 物理模型及計算方法

2．1 有限元網格

柔性接頭為軸對稱體，但由于加載過程中變形及載荷非對稱，采用三維有限元模型進行數值模擬，彈性件和防熱套選擇六面體八節點的SOLID 185號單元，增強件選擇SOLID 45號單元，各層彈性件、增強件沿厚度方向劃分3等份，沿寬度方向劃分20等份，沿圓周方向劃分30等份，見圖3。球坐標系(r，θ，φ)，坐標原點O位于柔性接頭幾何回轉中心，作動器位于φ=0°平面內。

2．2 邊界條件

對稱面φ=0°、180°施加對稱邊界條件，后法蘭上頂面、中頂面、外側面和防熱套的上外側面設為固定端，壓強載荷均勻作用于柔性接頭所有和氣體接觸的濕表面，在前法蘭的關鍵點上，施加等效的作動力載荷，模擬柔性接頭的擺動。

2．3 材料屬性

柔性接頭增強件及前后法蘭材料30CrMnSiA為線彈性材料，其彈性模量 E=205．8 GPa，泊松比 μ=0．3，彈性件采用二階四項式Mooney-Rivlin模型，描述其本構關系，利用橡膠材料的單軸拉伸、平面剪切試驗數據，擬合得到彈性件材料參數，如表2所示。

圖3 柔性接頭有限元計算網格Fig．3 Finite element computational meshes of flexible joint

表2 彈性件材料參數Table 2 Material parameter of elastormer

3 結果與分析

3．1 數值模擬與試驗結果對比

圖4是柔性接頭在不同容壓條件下，擺動6°時防熱套力矩數值模擬與試驗結果對比。

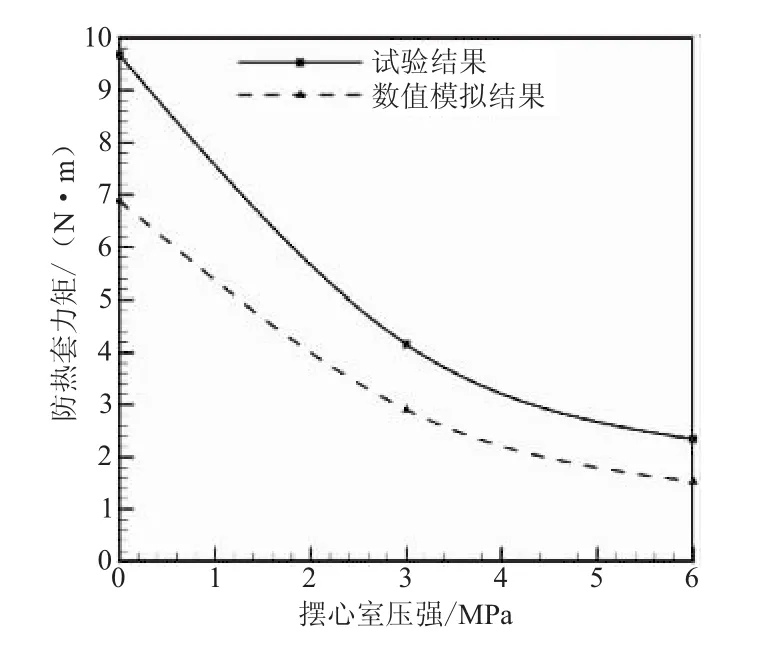
圖4 防熱套力矩數值模擬與試驗對比Fig．4 Experimental results compared with the simulation for the boot torque

從圖4可看出，防熱套力矩數值模擬與試驗結果數值吻合較好，且隨著容壓的升高，都呈現出減小的趨勢。數值上的差異主要原因有以下幾點:

(1)有限元建模并未考慮到防熱套的制造偏差，尤其是其在厚度上的偏差。

(2)防熱套處在復雜的應力應變狀態下，有限元模擬所選用的橡膠本構模型不能完全真實地模擬實際情況，導致計算結果有一定偏差。

3．2 壓強作用防熱套剪應力分布

圖5是防熱套在僅有壓強載荷時的剪切應力τrθ分布云圖。從圖5可看出，在僅有壓強載荷作用時，防熱套剪應力τrθ在同一個θ角度下沿環向(從φ=0°到φ=180°)均勻分布，考慮到球坐標系下應力的方向，任一個θ角度下的剪應力對擺心取矩之和都為0，接頭處于平衡狀態。從圖7(b)和圖7(c)防熱套在3 MPa和6 MPa容壓無擺動條件下φ=0°、180°剖面不同θ角度下的剪應力τrθ分布曲線可看出，在壓強載荷作用下，防熱套0°和180°剖面的剪應力有正有負，且基本呈對稱關系，這是由于防熱套與各層彈性件的粘接部分變形引起的。從應力云圖可明顯看出，不同φ剖面下防熱套形狀呈鋸齒狀，鋸齒狀凹進去的部分θ角較大的一側剪應力為負，θ角較小的一側剪應力為正。隨著壓強的增加，同一個θ角度下防熱套的剪應力τrθ的絕對值增大。而防熱套與增強件相粘接的部分剪應力較小，基本為0。

圖5 不同壓強載荷作用下防熱套剪應力τrθFig．5 Boot shear stress τrθ distribution at different pressure loads

3．3 壓強和作動器作用下防熱套剪應力分布

圖6是防熱套在不同容壓條件下，擺動6°時的剪應力τrθ的分布云圖，圖7防熱套是0°和180°剖面不同θ角度下的剪應力τrθ分布曲線。對比3 MPa和6 MPa僅有壓強載荷作用的情況，相同θ角度下0°剖面的剪應力τrθ相對于僅有壓強載荷作用時上升了，而180°剖面的剪應力則相對于僅有壓強載荷時下降了。依然是防熱套與彈性件粘接部分剪應力較大，防熱套與增強件粘接部分的剪應力τrθ變化不大，基本保持為0。

圖6 不同壓強擺角為6°載荷作用下防熱套剪應力τrθFig．6 Boot shear stress τrθ distribution at δ =6°with different pressure loads

3．4 防熱套力矩減小原因分析

防熱套的力矩可由接頭擺動引起的防熱套剪應力τrθ和τrφ對擺心取矩，并將所有的力矩投影到過擺心且垂直于 φ =0°、180°面的軸上求和得到［14］，計算式為

si為單元面積，一般τrφ較小，幾乎可忽略，力矩主要是由τrθ引起的，由接頭擺動時防熱套剪應力場在φ＜90°和φ＞90°產生的力矩方向相反，考慮到應力的方向問題，式(1)可簡化為

在防熱套上沿0°～180°取一路徑，如圖8所示。不同壓強下，剪應力τrθ沿該路徑的變化趨勢如圖9所示。

圖7 不同壓強載荷作用下防熱套0°和180°剖面剪應力τrθFig．7 Boot shear stress τrθ distribution at section φ=0°，180°with different pressure loads

從圖9可看出，容壓為0 MPa時，所選路徑上的剪應力 τrθ從 0°～180°以 90°為分界線呈正負交替，將接頭以φ=90°分為左右兩個部分，在φ＜90°的區域剪應力為正時，產生正的防熱套的力矩，而在φ＞90°的區域剪應力為負時，產生正的防熱套力矩，故此時的防熱套力矩等于正負剪應力對擺心力矩的絕對值之和。隨著容壓的升高，所選路徑上的剪應力τrθ的負值區域逐漸減小，正值區域逐漸擴大。當容壓達到6 MPa時，所取路徑上的剪應力τrθ都為正值。此時，φ＜90°和φ＞90°兩側計算出的力矩方向相反，防熱套力矩為兩側剪應力對擺心力矩的絕對值之差。雖然隨壓強升高，φ＜90°區域的剪應力值有所增大，但增大的幅度不如φ＞90°的區域，從圖中的方格面積可定性看出。因此，隨著容壓升高，防熱套力矩逐漸減小，這對小型柔性噴管在高室壓下的工作是有利的。

圖8 所取路徑示意圖Fig．8 diagram of selected path

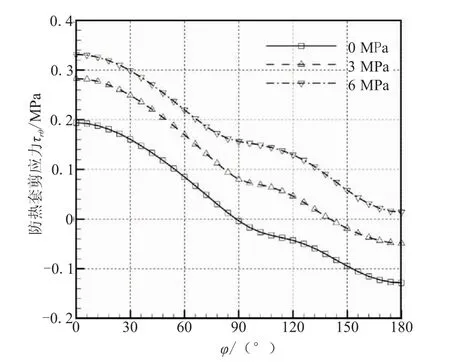
圖9 所選路徑剪應力τrθ隨壓強的變化Fig．9 Changes of τrθ on selected path at different pressures

4 結論

(1)采用“二階四項式”超彈本構模型，模擬硅橡膠的本構關系，可得到較符合實際的結果;

(2)在壓強和作動器作用下，纏裹式防熱套與增強件粘接部分剪應力τrθ較小，與彈性件粘接的部分剪應力τrθ較大，是產生防熱套力矩的主要原因;

(3)隨著容壓的提高，6°擺角下防熱套力矩逐漸減小，有利于小型柔性接頭的使用，這是由其剪應力τrθ的分布變化引起的。

［1］ 王錚，胡永強．固體火箭發動機［M］．北京:宇航出版社，1993．

［2］ Shimon Shani，Shlomo Putter，Arie Peretz，et al．Development of a high-performance flexible joint for thrust vector control［R］．AIAA 95-3017．

［3］ 林培基，高峰．推力矢量對防空導彈作戰效能的影響［J］．飛航導彈，2009(1):56-57，64．

［4］ 吉禮超，宋貴寶．防空導彈控制方法的研究現狀及展望［J］．戰術導彈技術，2009(3):54-59．

［5］ Wassom S R，Faupell L C，Perley T．Integrated aerofin/thrust vector control for tactical missiles［J］．Journal of Propulsion and Power，1991，7(3):374-381．

［6］ Caveny L H，Geisler R L，Ellis R A，et al．Solid rocket enabling technologies and milestones in the united states［J］．Journal of Propulsion and Power，2003，19(6):1038-1066．

［7］ Olsen K E，Walsh J J，Thomas E L．Navy terrier LEAP thirdstage propulsion［C］//AIAA Missile Sciences Conference．Monterey，CA，November 7-9，1994．

［8］ Uhrig G，Roussille C．Design drivers and technologies for solid propulsion of interceptors［C］//1st AAAF International Conference on Missile Defense．Arcachon，France，February 3-5，2003．

［9］ Avio．Aster 30［EB/OL］．http://www．aviogroup．com/files/catalog/pdf/motore_per_aster_30_25．pdf．

［10］ Woodberry R F H，Zeamer R J．Solid rocket thrust vector control［R］．NASA SP-8114，1974．

［11］ Lui C Y．Asbestos-free nozzle flexible boot load characterization for the space shuttle solid rocket booster［R］．AIAA 96-2778．

［12］ 張曉光，劉宇，任軍學，等．小型柔性接頭推力矢量性能試驗研究［J］．航空動力學報，2012，27(12):2836-2841．

［13］ 陳汝訓，劉銘初，李志明，等．固體火箭發動機設計［M］．北京:中國宇航出版社，2005．

［14］ 王春光，史宏斌，王雪坤，等．高壓下噴管柔性接頭擺動力矩數值分析［J］．推進技術，2011，32(2):202-206．