三捷聯慣組冗余系統故障檢測閾值設計方法①

王易南，陳 康，閆 杰

(1．北京宇航系統工程研究所，北京 100076;2．西北工業大學 航天學院，西安 710072)

0 引言

捷聯式慣導系統(Strap-down Inertial Navigation System)是把慣性儀表直接固聯在載體上，用計算機來完成導航電子平臺功能的慣性導航系統。在SINS中，慣性組件(陀螺儀和加速度計)是導航與控制系統的關鍵部件，通常是控制系統中容易發生故障的部分并易受不良環境的影響。因此，慣導系統的故障檢測與診斷設計是提高可靠性的一種重要手段。

故障檢測與診斷所采用的方法主要有基于硬件冗余的診斷法［1－2］、基于解析冗余的診斷法［3－4］、基于知識的診斷法［5］和基于信號處理的診斷法［6］。其中，基于硬件冗余的診斷法是最早也是目前最有效的一種診斷方法。在該方法中，對于故障閾值的計算是一項關鍵技術，最常用的方法是廣義似然比方法(GLT)［7］。此外，還有基于構造測量值統計量的均值檢驗法［8］和基于樣本加權的均值檢驗法［9］。

本文從工程角度出發，基于實際的慣組平臺進行動態閾值的設計方法研究，并對其故障診斷效果進行了分析。

1 研究對象

本文研究的3套捷聯慣組采用共支架，共基準的安裝方式，由6個光纖慣組與3個激光慣組構成，如圖1所示。

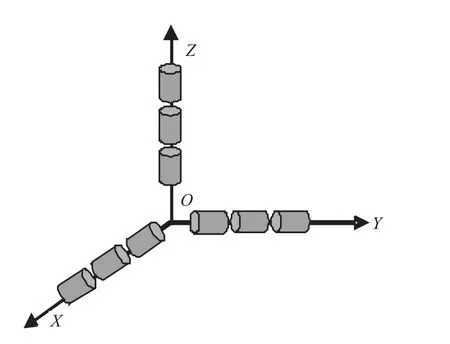
圖1 3套慣組同軸安裝示意圖Fig．1 Coaxially mounted IMUs

2 慣組誤差模型

2．1 陀螺誤差模型

陀螺器件的誤差模型可表示為

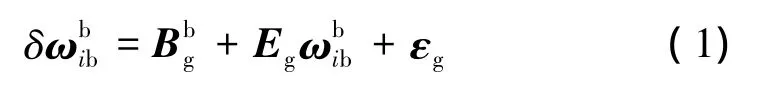
即

2．2 加速度計誤差模型

加速度計器件的誤差模型可表示為

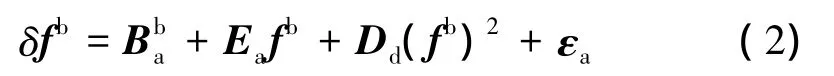
即

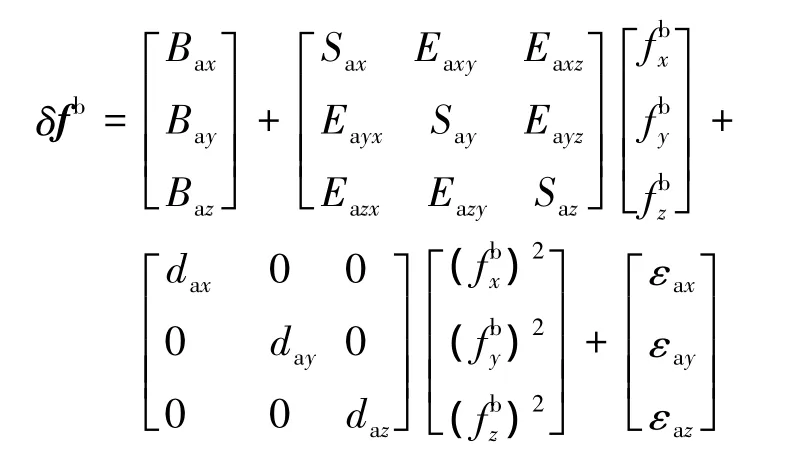
3 三捷聯慣組動態閾值設計

當慣組器件輸出形式為脈沖時，2個器件輸出之間的差值一定是脈沖的整數倍，就意味著只要2個器件的輸出值不一樣，它們之間的差值就會超出閾值，這顯然不符合實際。因此，當器件以脈沖形式輸出時，只能采用均值法進行閾值設計。

3．1 數據窗均值法

具體實施步驟:

(1)采用蒙特卡洛打靶生成脈沖輸出值(如生成1 000條彈道的陀螺和加速度計的脈沖輸出)。

(2)將同一物理量的3個傳感器各時刻輸出值P1j(t)、P2j(t)、P3j(t)兩兩相減，得到 3個差值序列，生成 x1=P1j(t)－P2j(t)，x2=P2j(t)－P3j(t)，x3=P1j(t)－P3j(t)的差值數據，采用kolmogorov-smirnov檢驗法對其進行檢驗，發現此時數據不服從正態分布，且無法詳細地獲取其分布狀態。以x1為例，{x1(t)，x1(t+t0)，…，x1(t+(N－1)t0)}同分布，由中心極限定理可知，當N足夠大時服從正態分布。

(3)選擇數據窗長度N(如N=1 000)，以連續N個數據xi(tk－N+1)，…，xi(tk)的平均值為系統故障檢測數據。

連續N(1 000)個數據的選取方法如圖2所示。

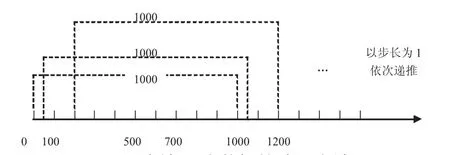
圖2 連續N個數據的選取方法Fig．2 Method to select continuous data

3．2 分位數法閾值置信區間估計

通過kolmogorov-smirnov正態分布檢驗法進行數據檢驗，對于不服從正態分布的樣本，需要確定其大致的分布狀態。

對樣本數據進行升序排序，將相同的數值合并，計算每一個數據在原樣本數據中出現的次數占整體數據的比例，得到每個樣本數據的出現概率。

在第一個窗長度以內的某一個時刻，找出平均數量比較小的一組樣本，由于其累積次數不足，信息量不夠大，但能反映出數據的大致分布規律，其概率分布圖如圖3所示。結合圖3分析數據，發現樣本數據依然較為規則地分布于0的兩側，小樣本(絕對值)出現的概率大，大樣本(絕對值)出現的概率小。結構相似于正態分布，但由于樣本量較小，無法精確判斷其結果。

在取出第一個窗長度后的對不服從正態分布的樣本，計算其樣本分布概率如圖4所示。結合圖4分析數據，此樣本依然規則地分布于0值附近，大樣本(絕對值)出現的概率大，小樣本(絕對值)出現的概率小，類似于正態分布，但未通過嚴格的正態分布測試。

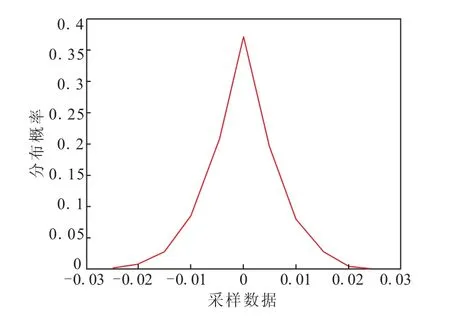
圖3 第一個窗口長度內數據概率分布圖Fig．3 Probability distributions of the data in the first window

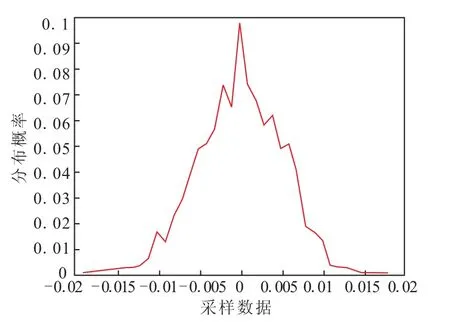
圖4 從第二個窗口開始數據概率分布圖Fig．4 Probability distributions of the data in the second window

針對于這種特殊的情況，采用P分位數的方法來計算閾值，假設當前的置信度為1－α。求解置信區間時，需要求出的區域能最大限度地占據數據出現可能性最大的區域。針對于當前樣本數據概率對稱分布的狀態，對稱分配 2 個 P 分位數 Pα/2和 P1－α/2，通過此兩點確定出置信上下界。

3．3 正態分布法閾值置信區間估計

對數據窗均值法處理后的數據，若其服從正態分布，均采用正態分布法進行置信區間的估計。

總體 X 服從正態分布 N(μ，σ2)，其中［X1，…，Xn］T為來自總體的一個樣本μ、σ未知，使用最大似然估計的方法估計出μ和σ的值得到總體X正態分布的分布密度為

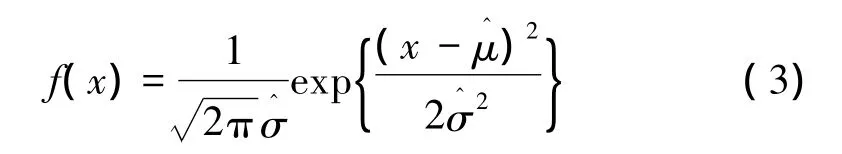
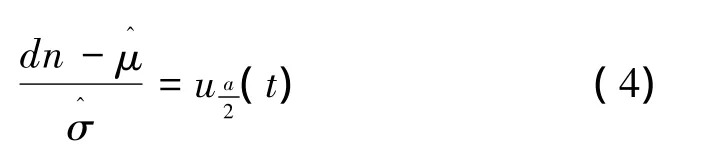
置信上界up滿足:^

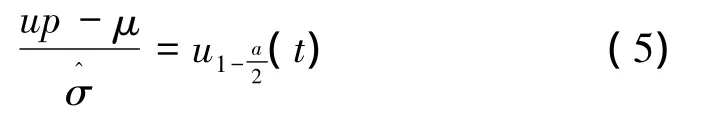
故x的置信度為1－α的置信區間為

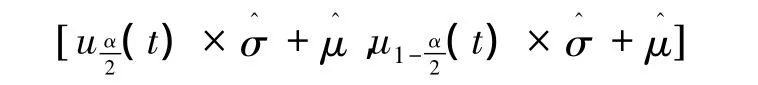
3．4 閾值分段設計

(1)將通過概率統計法得到的閾值，按時間變化逐序進行差分，即可判斷出其各個時刻點數據閾值的變化情況;

(2)選擇其變化率最大的時刻點為分段點，然后分析各時間段的閾值數據，取其最大最小值分別作為此時間段的閾值上下限。

以慣組1和慣組2在X軸方向上的繞質心旋轉角速度脈沖值差值為例，其閾值變化曲線如圖5所示。慣組1和慣組2在X軸方向上的繞質心旋轉角速度脈沖值差值變化曲線有11個很明顯的拐點，此處其變化率最大，對此數據求解一階導數，如圖6所示，取其變化率最大的點為閾值分段點，然后分析各個分段區間內的數據變化，取此段區間的最大最小值分別為此段區間的閾值上下限，則分段后的閾值上限變化曲線如圖7所示。

4 三捷聯慣組故障檢測方法

故障診斷方法采用門限表決方法，其主要流程如下:

(1)在運載火箭飛行過程中，實時測量同一物理量的3個傳感器測量值 P1j(t)、P2j(t)、P3j(t)，計算P1j(t)－P2j(t)，P2j(t)－P3j(t)，P1j(t)－P3j(t)值，并判斷其是否落入置信區間內。

當P1j(t)－P2j(t)落入置信區間，記 ε1=1，否則記ε1=0;

當P2j(t)－P3j(t)落入置信區間，記 ε2=1，否則記ε2=0;

當P1j(t)－P3j(t)落入置信區間，記 ε3=1，否則記ε3=0。

(2)當ε1+ε2+ε3=2時，判斷傳感器未出現故障。取慣組1輸出量為慣導輸出量，進行慣導解算。

(3)當 ε1+ε2+ε3=1，則可依據服從多數原則，判定一個傳感器發生了故障，即判斷出現1°故障。

當ε1=1時，判斷慣組3傳感器故障，取慣組1輸出量為慣導輸出量進行，慣導解算;

當ε2=1時，判斷慣組1傳感器故障，取慣組2輸出，為慣導輸出量進行，慣導解算;

當ε3=1時，判斷慣組2傳感器故障，取慣組1輸出量為慣導輸出量進行，慣導解算。

(4)當 ε1+ε2+ε3=0 時，判斷出現 2°故障。這種情況需要進一步研究，可依據傳感器信號輸出的頻域特性、基準彈道指令等輔助手段來進行故障判斷。

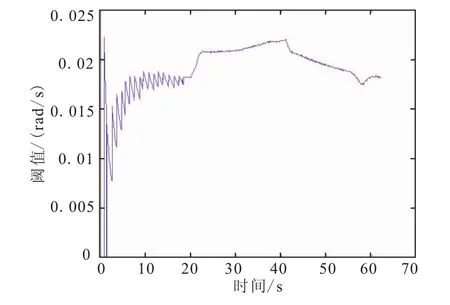
圖5 閾值變化曲線Fig．5 The threshold curve

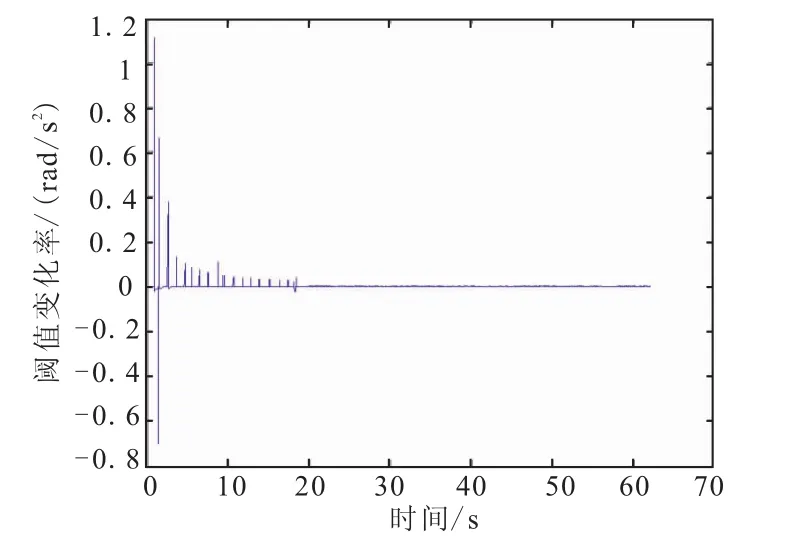
圖6 閾值變化率曲線Fig．6 The rate of threshold changing

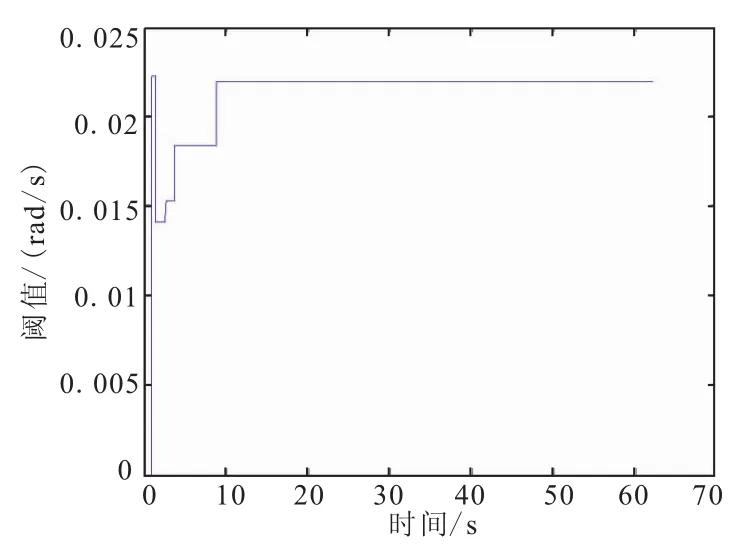
圖7 分段后的閾值上限變化曲線Fig．7 The upper limit curve

5 檢測結果及分析

故障模型主要包括輸出故障和參數故障:參數故障是指(零次項、標度因數等)變化引起的突變和線性、正弦、方波漂移的緩變故障;輸出故障是包括常零值、滿量程及倍頻率輸出。

本文以對IMU3在Z軸上的陀螺注入零次項參數方波故障為例，其開始注入故障時刻為20 s時，故障幅值分別為 5、10、20、50、100°/h，頻率分別為1、5、20 Hz，仿真100次，檢測結果如圖8所示。

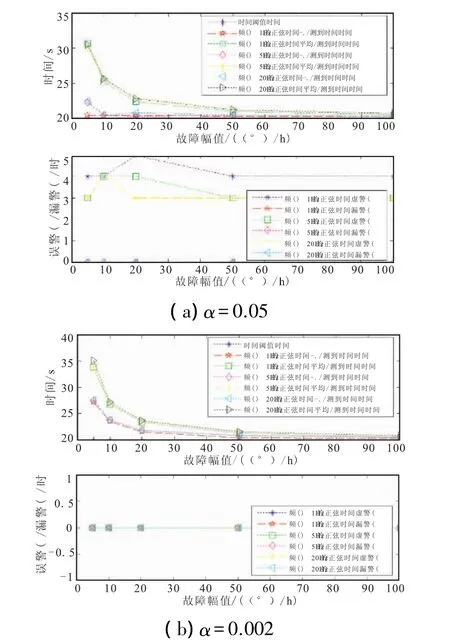
圖8 統計置信水平α為0．05和0．002時的仿真結果Fig．8 Simulation results when the confidence level is 0．05 and 0．002

由圖8可見，將統計置信水平 α=0．05和 α=0．002條件下的仿真結果相比較:前者最早檢測到故障時間和平均檢測到故障時間比后者相對早一些，隨著注入故障幅值的增大，其最早檢測到故障時間和平均檢測到故障時間都逐漸縮短，但隨著注入故障頻率的增大，其最早檢測到故障時間和平均檢測到故障時間會逐漸增長;前者誤警率明顯升高，其誤警率約在3%～5%之間，而后者的誤警率為0%。然而，兩者的誤警率都嚴格控制在5%的范圍內，漏警率均為0%，完全滿足本次仿真的指標要求。

6 結論

(1)針對共支架、共基準方式安裝的三捷聯慣組冗余系統，建立了陀螺和加速度計的誤差模型，進行了蒙特卡洛仿真并量化處理，得到了3套陀螺和加速度計的脈沖輸出。

(2)慣組器件的脈沖當量對慣組冗余系統的閾值區間的分布有較大影響，脈沖當量越小，閾值區間的分布越趨近于標準正態分布。在脈沖當量較大的情況下，部分閾值區間不服從正態分布，但可通過分位數法進行解算。

(3)使用數據窗均值法得到的閾值區間能夠反映出載體機動對慣組系統閾值的影響，根據閾值的變化率，可動態地計算分段閾值。

(4)根據此方法計算的閾值能夠有效地檢測到三捷聯慣組中發生故障的陀螺或加速度計，且檢測到故障時間、漏警率和虛警率均滿足指標要求。

［1］ 王仲生．職能故障診斷與容錯控制［M］．西安:西北工業大學出版社，2005．

［2］ 吳今培．職能故障診斷技術的發展與展望［J］．振動、測試與診斷，1999(2):79-86．

［3］ 吳今培，肖建華．智能故障診斷與專家系統［M］．北京:科學出版社，1997:1-77．

［4］ Umar Iqbal Bhatti，Washington Yotto Ochieng．Failure modes and models for integrated GPS/INS systems［J］．The Journal of Navigation，2007，60:327-348．

［5］ Umar I Bhatti，Washington Y Ochieng，Shaojun Feng．Integrity of an integrated GPS/INS system in the presence of slowly growing errors［J］．GPS Solut ，2007，11:173-181．

［6］ 張玲霞．導航系統故障檢測與診斷及其相關理論問題的研究［D］．西安:西北工業大學，2004．

［7］ 潘鴻飛，任尚云，袁立群．捷聯慣導系統故障檢測與處理技術研究［J］．上海航天，2002(6):37-39．

［8］ 錢華明．故障診斷與容錯技術及其在組合導航系統中應用研究［D］．哈爾濱:哈爾濱工程大學，2004:80-86．