利用矩陣初等變換求二維射影變換

周明旺

(連云港師范高等專(zhuān)科學(xué)校 數(shù)學(xué)與信息工程學(xué)院，江蘇 連云港 222006)

二維射影變換是高等幾何的核心內(nèi)容之一，由無(wú)三點(diǎn)共線(xiàn)的四對(duì)對(duì)應(yīng)點(diǎn)唯一確定。然而其射影變換式的求解在教材中采用的是由12 個(gè)線(xiàn)性方程求13 個(gè)未知量比值的方法，計(jì)算量很大。基于上述原因另辟新徑，利用矩陣的初等變換知識(shí)給出了二維射影變換基本定理的一種新證法，進(jìn)而給出二維射影變換的矩陣算法。這樣以來(lái)不單簡(jiǎn)化了計(jì)算，更重要的是對(duì)于密切學(xué)科間的滲透、思想觀(guān)念的更新、思維方法的訓(xùn)練、探究能力的培養(yǎng)等方面起著重要作用。［1］

1 預(yù)備知識(shí)

定義1 設(shè)在點(diǎn)場(chǎng)π 與π/上各建立了齊次射影坐標(biāo)系，x = (x1，x2，x3)，x/= (x/1，x/2，x/3)分別是其上點(diǎn)的射影坐標(biāo)，如果映射φ:π →π/可以表示成

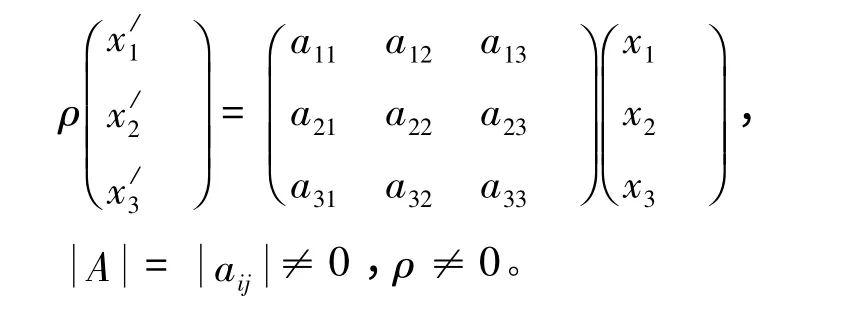
則稱(chēng)φ 是π 到π/的二維射影對(duì)應(yīng)。特別地，若π/= π，則稱(chēng)φ 是π 上的二維射影變換。［2］

引理1 設(shè)A，B，C 為平面上不共線(xiàn)三點(diǎn)，其齊次坐標(biāo)分別為a，b，c，則平面上任一點(diǎn)的齊次坐標(biāo)可以表示為la +mb +nc，其中l(wèi)，m，n ∈R，且l2+m2+ n2≠0 。［2］

定義2 設(shè)A，B，C，D 為平面上無(wú)三點(diǎn)共線(xiàn)的四點(diǎn)，適當(dāng)選取其齊次坐標(biāo)分別為a，b，c，d，若d= a+b+c，則稱(chēng)a，b，c，d 為點(diǎn)A，B，C，D 的規(guī)范化齊次坐標(biāo)。

2 主要結(jié)果

其中l(wèi)，m，n ∈R，且lmn ≠0 ，

則la，mb，nc，d 是A，B，C，D 的規(guī)范化齊次坐標(biāo)。

證明:因?yàn)閷?duì)矩陣施行初等行變換不改變列向量的線(xiàn)性關(guān)系。［3］

對(duì)于

即d = la+mb+nc，所以la，mb，nc，d 是A，B，C，D 的規(guī)范化齊次坐標(biāo)。

定理2 射影平面上任意的兩個(gè)四點(diǎn)組(其中各組內(nèi)均無(wú)三點(diǎn)共線(xiàn))，則存在唯一的二維射影變換。［4］

下證A 的存在性與唯一性。

由φ P( )i = P/i，i = 1，2，3，4。則

由引理1，存在全不為零的λ1，λ2，λ3使得P4= λ1P1+ λ2P2+ λ3P3，同理存在全不為零的使得于是

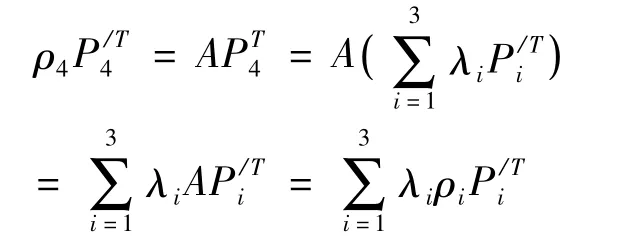
而對(duì)于ρ4的不同取值，結(jié)合點(diǎn)的齊次坐標(biāo)的性質(zhì)知:射影變換是相同的，即射影變換唯一。……