三角網格上基于Lebesgue常數最小的混合有理插值

朱六三，趙前進

（安徽理工大學理學院，安徽 淮南232001）

0 引言

近年來，基于連分式的二元有理插值方法被廣泛關注。檀結慶在文獻［1-2］中通過對Newton多項式插值和Thiele型連分式插值進行加工，用類似于張量積的方法構造了Newton-Thiele和Thiele-Newton兩種二元混合有理插值。趙前進在文獻［3-4］中通過對插值節點集進行分塊構造了基于塊的混合有理插值，但連分式插值會受到可能有不可達點、偏逆差商不存在等瓶頸問題的制約。另外，連分式插值無法避免極點同時又難以控制極點的位置。1945年，W.Taylor發現了多項式插值的重心公式，1984年，W.Werner給出了重心有理插值方法［5］。利用權的符號可判定重心有理插值在插值區間內的極點個數，通過適當選擇權可使重心有理插值避免極點和不可達點［6］。基于重心有理插值和Newton多項式插值，趙前進和杜繼亮在文獻［7］中構造了上三角網格上的混合有理插值方法用來逼近連續的已知函數。然而，文獻［7］中的方法不能用于逼近被插值函數未知的情形。為此，本文在上三角網格上構造重心——牛頓有理插值，應用Lebesgue常數最小建立優化模型，解得最優權。給出了數值實例來表明新方法所得的二元有理插值繼承了重心有理插值的計算量小、數值穩定性好、沒有極點以及可以避免不可達點等優點。

1 基于上三角網格的重心-牛頓混合插值

設上三角網格

（c）wi（i＝0，1，…，n）分別為x0，x1，…，xn對應的插值權。

由文獻［7］知，只要所有的權wi（i＝0，1，…，n）均不為零，則上述有理函數R（x，y）滿足插值條件。

2 上三角網格基于Lebesgue常數最小的重心-牛頓混合插值

在公式（1）中，選擇不同的權可得不同的重心-牛頓混合插值。文獻［7］中，當被插值函數為表達式已知的連續函數時，以插值權為決策變量、插值平方誤差為目標函數、以有理函數R（x，y）無不可達點、無極點為約束，增加權的規范化約束條件，建立了優化模型求解最優權。本文研究當被插值函數為表達式未知時，基于Lebesgue常數

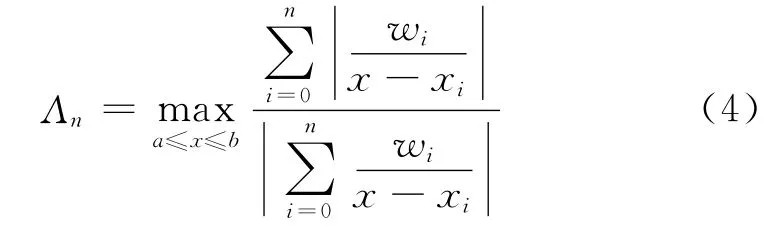
最小為目標函數，以有理函數R（x，y）無不可達點、無極點為約束，增加權的規范化約束條件，建立如下優化模型求解最優權：

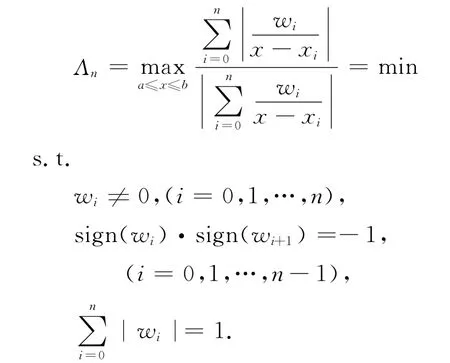
最后使用LINGO優化軟件計算出最優權。

3 數值實例

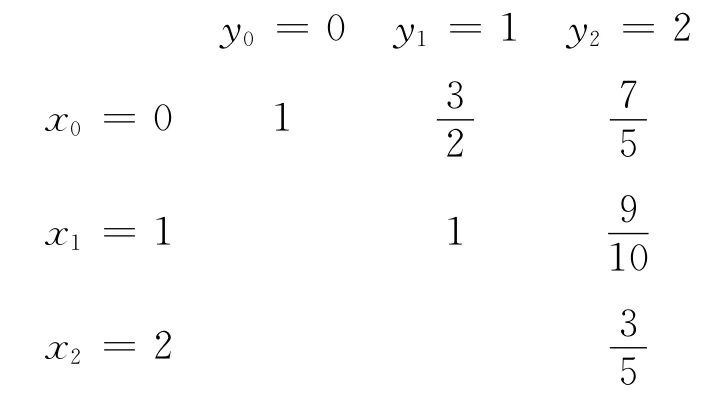
記上三角網格上基于Lebesgue常數最小的重心-牛頓有理插值為R1（x，y），文獻［7］中的有理插值記為R2（x，y），文獻［8］中記為R3（x，y）。被插值函數與插值函數R1、R2、R3的圖像以及誤差比較如下：

圖1 f（x，y）

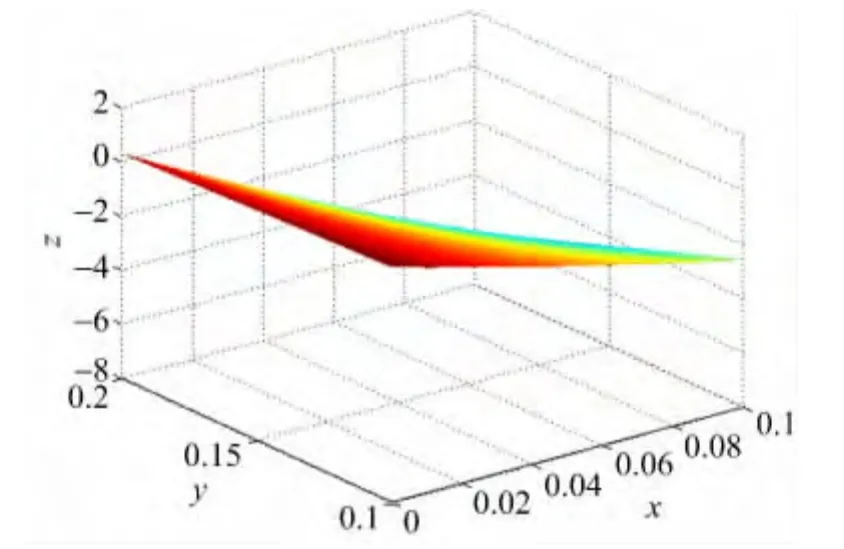
圖2 R1（x，y）

圖3 R2（x，y）

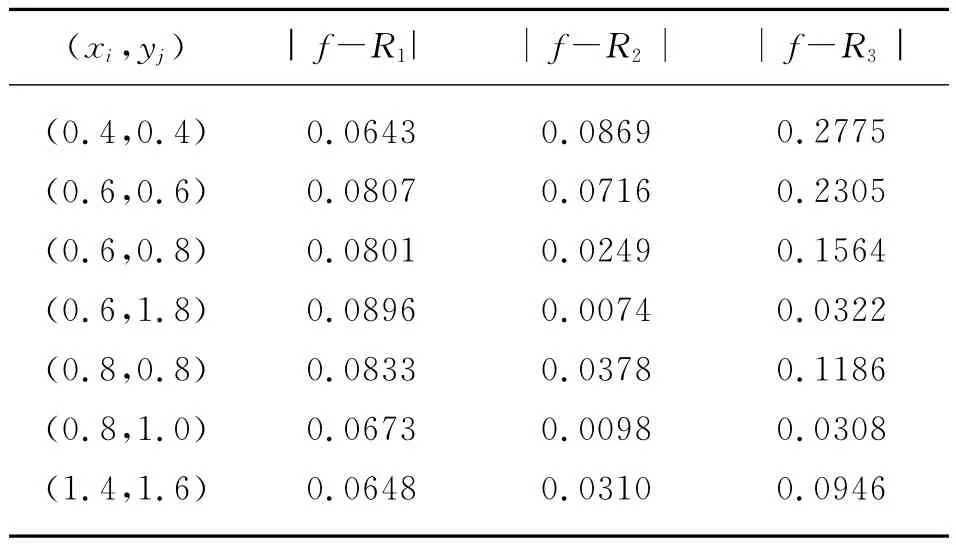
表1 插值誤差的比較

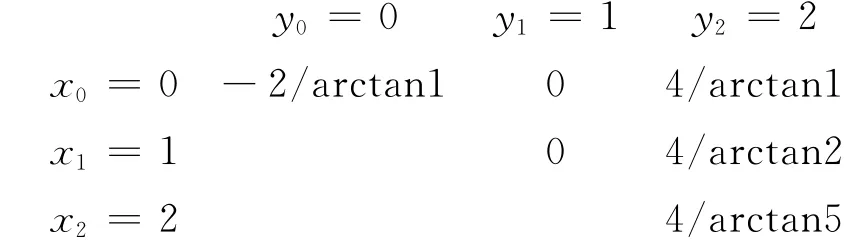
記本文方法求得的混合有理插值為，

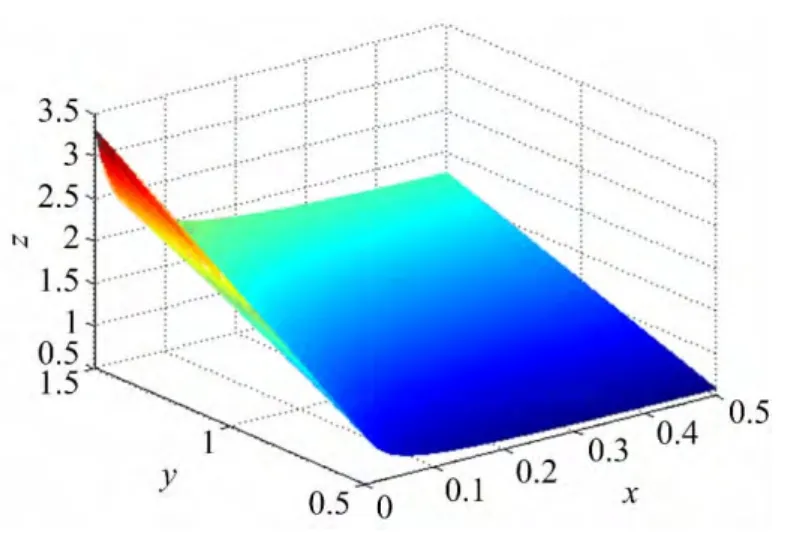
圖5 f（x，y）

可見，利用本文方法得到的插值函數與文獻［7］中得到的插值函數的逼近效果甚好，均明顯好于文獻［8］中插值函數的逼近效果，值得注意的是，本文方法適用于被插值函數表達式未知情形。

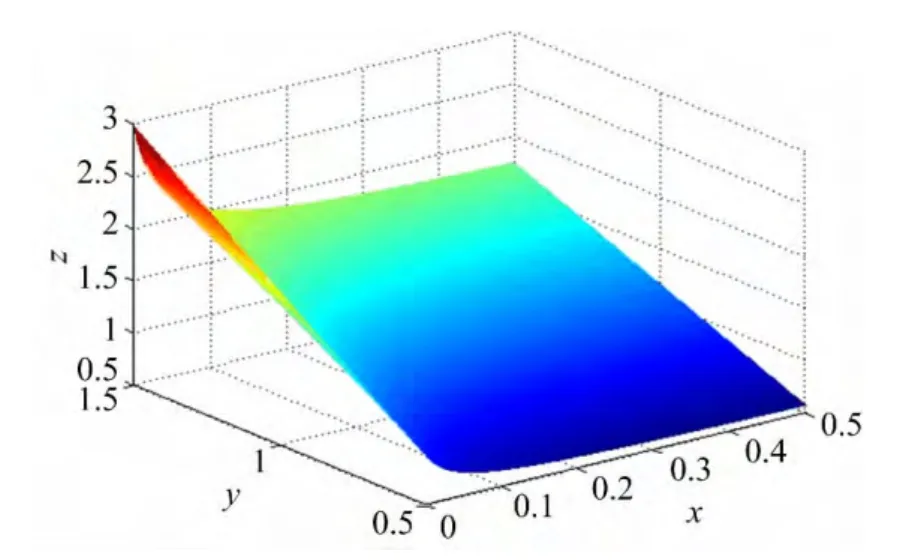
圖6 R（x，y）

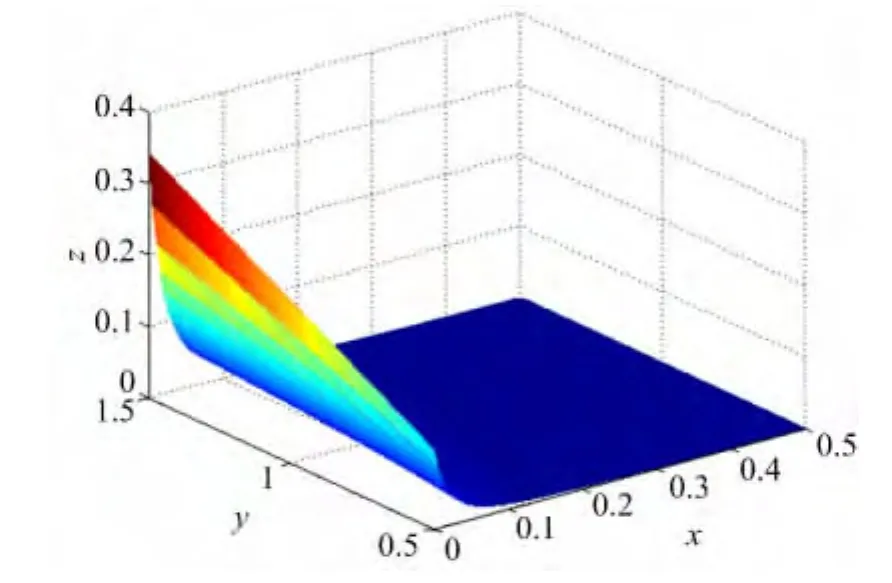
圖7 ｜f（x，y）-R（x，y）｜

4 結論

本文利用Lebesgue常數最小為目標函數求得三角網格上重心-牛頓有理插值的最優權，使得該混合插值方法在被插值函數的表達式未知時仍可使用。給出的數值實例表明了新方法的有效性。

［1］Tan J，Bivariate Blending Rational Interpolants［J］.Approx.Theory ＆Its Appl，1999，15（2）：74-83.

［2］Tan J，Fang Y，Newton-Thiele's Rational Interpolants［J］.Numerical Algorithms，2000（24）：141-157.

［3］Zhao Q J，Tan J Q.Block Based Newton-like Blending Rational Interpolation［J］.Journal of Computational Mathematics，2006，24（4）：515-526.

［4］Zhao Q J，Tan J Q.Block Based Thiele-like Blending Rational Interpolation［J］.Comput Appl Math，2006（195）：312-325.

［5］Schneider C，Werner W，Some new aspects of rational interpolation［J］.Math.Comp，1986，47（175）：285-299.

［6］Schneider C，Werner W，Hermite Interpolation：The Barycentric Approach［J］.Computing，1991，46（1）：35-51.

［7］Qianjin Zhao，Jiliang Du，The New Bivariate Rational Interpolation Over The Triangular Grids.2012IEEE International Conference on Computer Science and Automation Engineering，CSAE 2012，pp 780-784，Zhangjiajie，China，2012.

［8］Yu Xiaolei，Construction of New Bivariate Blending Rational Interpolation over the Triangular Grids ［C］.ICISS，2010.