導彈編隊隊形拆分重構與領彈繼任控制器設計*

郝 博，李 帆，趙建輝，薛 蕾

(北京航空航天大學儀器科學與光電工程學院，北京 100191)

0 引言

導彈編隊因能使多枚協同作戰的導彈更具攻擊性和防御性，具有較強的研究需求牽引。導彈編隊隊形控制問題包括:隊形的保持、拆分以及重構、領彈繼任[1]。導彈編隊在飛行過程中，為避免與山體碰撞或受到地方火力攻擊，需要進行隊形的變換以避開威脅區，之后恢復原隊形飛行，即隊形的拆分和重構;而當編隊領彈被擊落后，為繼續指揮戰斗，某一跟隨彈必須馬上繼任為領彈，即領彈繼任。

目前常用的編隊控制算法主要有PID控制算法[2]、模糊控制算法[3]、基于行為的控制算法[4]、虛擬結構法[5]等，PID控制算法簡單但難以處理強耦合的系統;模糊控制算法有時候難以建立模糊規則;基于行為的控制算法難以定義和用數學方法分析群體的行為，且編隊穩定性較差;而虛擬結構法難以進行容錯處理，且通訊量大，可靠性差。

文中針對導彈編隊中的隊形拆分重構與領彈繼任設計了基于自適應控制的控制器，可修正控制器本身特性以適應突發威脅和領彈被擊落后的隊形變換。較之上述文獻算法，該算法操作簡單，易于實現，且具有較強的魯棒性和穩定性。

1 導彈編隊飛行控制系統

1.1 隊形的編排

常見隊形主要包括:平行、楔形、菱形、縱向編隊等，如圖1所示。文中以3枚導彈組成的楔形編隊為例，其領彈飛行彈道高，視野好，可通過數據鏈與跟隨彈進行通信，將所探測敵情數據發送給跟隨彈。文中的隊形控制器亦適用于其他編隊隊形。

圖1 常見編隊隊形

1.2 編隊中單枚導彈運動學模型

文中編隊隊形采用慣性坐標系(或地面坐標系)Oxyz和彈道坐標系Ox2y2z2，二者的變換關系為:

其中:V、ψV、θ為導彈的速度、彈道偏角、彈道傾角。為簡便起見，文中將ψV記為ψ;X、Y、Z為慣性坐標系的位置坐標值。

1.3 編隊飛行控制系統

導彈編隊飛行控制系統控制領彈和跟隨彈按照預定的隊形飛行，主要由領彈穩定、跟隨彈穩定、隊形保持、隊形拆分和重構控制及領彈繼任控制5個回路組成，控制系統結構如圖2所示。

圖2 導彈編隊飛行控制系統

其中:Vcl、θcl、ψcl和 Vcf、θcf、ψcf分別為領彈和跟隨彈的指令速度、彈道傾角和彈道偏角;Vl、θl、ψl和 Vf、θf、ψf分別為領彈和跟隨彈的實際速度、彈道傾角和彈道偏角。

2 導彈的穩定回路的控制設計

建立領彈和跟隨彈簡化的一階運動模型[6]，在每枚導彈都有標準的閉環自動駕駛儀的情況下，導彈可以通過控制各自的馬赫數保持自動駕駛儀、彈道偏角保持自動駕駛儀和彈道傾角保持自動駕駛儀使其按參考信號來飛行，領彈和跟隨彈互相解耦的自動駕駛儀可寫成式(2)和式(3)形式。

其中，τv、τψ、τθ分別為速度、彈道偏角和彈道傾角控制通道的慣性時間常數;只要設計跟隨彈的Vcf、ψcf、θcf，使跟隨彈和領彈的相對距離位置達到要求的期望值，即可實現導彈避障過程中的隊形拆分、重構以及領彈繼任。

3 編隊導彈的隊形自適應控制設計

領彈和跟隨彈的相對位置關系為:

其中:Xl、Yl、Zl和 Xf、Yf、Zf分別為領彈和跟隨彈在慣性坐標系下的坐標值，R (ψf，θ)f為彈道坐標系到慣性坐標系的轉換矩陣，xf、yf、zf為領彈和跟隨彈的相對距離，領彈和跟隨彈在慣性坐標系下質心運動的運動學方程為:

對式(5)～式(10)求導并與式(2)、式(3)代入式(12):

由式(13)和式(14)可得:

其中:k1、k2為對角陣。當θ2≠± π/2，且V2≠0時，G－1存在，即:

式(16)即為跟隨彈跟隨領彈的自適應控制律。

4 仿真實驗

4.1 編隊導彈的隊形拆分、重構控制仿真

編隊初始狀態為3枚導彈組成的楔形編隊，為使領彈與各跟隨彈保持良好的通訊能力，文中將隊形拆分為縱向隊形，由領彈對跟隨彈進行集中式控制，規避威脅后重構為楔形隊形，如圖3所示。

設3枚導彈以時速300m/s勻速飛行，初始彈道偏角和彈道傾角均為 0°，時間常數為 τv=4，τψ=4，τθ=4，仿真步長為0.01s，假設領彈和跟隨彈的初始相對坐標為(120m，150m，100m)，其中:

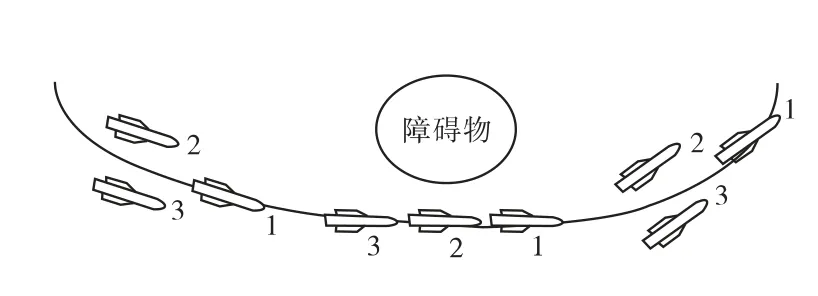
圖3 領彈和跟隨彈的隊形拆分和重構圖

當領彈1遇到威脅后開始機動，其速度大小和彈道傾角不變，彈道偏角按如下規律變化:

此時，導彈編隊隊形拆分為縱向編隊，要求跟隨彈2和3最終與領彈1處于同一高度，且與領彈1的距離分別保持在200m、400m，以跟隨彈2為例，其與領彈1的速度、彈道傾角、彈道偏角及彈道距離仿真結果如圖4所示。

圖4 領彈1和跟隨彈2的各變量變化圖

編隊飛出威脅區后，3枚導彈重構為楔形隊形。此時要求3個方向距離始終保持(200m，300m，150m)不變，設領彈做如下機動:

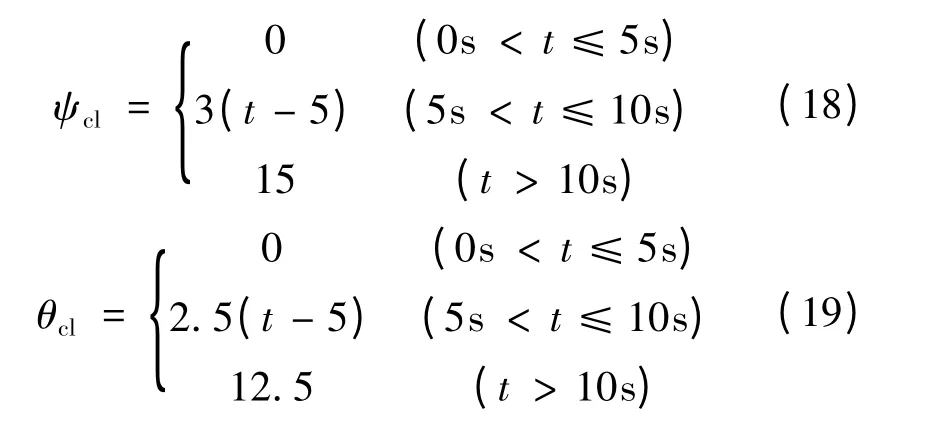
領彈和跟隨彈其他參數設置與上文相同，以跟隨彈3為例，其與領彈1的速度、彈道偏角、彈道傾角和彈道距離如圖5所示。

圖5 領彈1和跟隨彈3的各變量變化圖

由圖4和圖5可見，導彈編隊在遇到突發威脅時，進行隊形的拆分，20s后導彈編隊即可達到期望的隊形，對于時速300m/s的巡航導彈，只需在到達障礙物6km探測到威脅信息即可，而一般導引頭雷達的探測距離至少在10km以上，因此，可滿足時間要求，在繞過威脅區后，導彈編隊可恢復為穩定的楔形隊形，且各自的速度、彈道偏角、彈道傾角以及3個方向的彈道距離保持不變。

4.2 領彈繼任控制仿真

設跟隨彈2和跟隨彈3之間3個方向距離為(0m，0m，300m)，當領彈1被擊落時，跟隨彈2爬升到領彈1位置繼任為領彈2，要求領彈2和跟隨彈3之間3個方向距離為(200m，150m，0m)，導彈由楔形編隊變為縱向編隊，變換過程如圖6所示。

設導彈2按式(20)和式(21)進行機動爬升到領彈1的位置。領彈2和跟隨彈3的速度、彈道偏角、彈道傾角和彈道距離如圖7所示。

圖6 領彈被擊落時編隊隊形變換

圖7 領彈2和跟隨彈3的各變量變化圖

由圖7可見，跟隨彈2爬升為領彈2后，跟隨彈3進行隊形變換，可達到要求的期望值，且各自的速度、彈道偏角、彈道傾角以及3個方位的彈道距離保持不變，導彈編隊能夠在編隊機動情況下快速恢復穩定隊形，顯示出了較強的魯棒性和穩定性。

5 結論

文中設計了基于自適應控制的導彈編隊隊形拆分、重構與領彈繼任控制器以滿足導彈編隊協同作戰的任務需求。首先提出了以隊形為基礎的編隊飛行控制系統結構;其次建立了導彈在慣性坐標系下的運動模型;然后從領彈和跟隨彈的相對位置出發，設計了基于自適應控制的編隊隊形拆分重構與領彈繼任控制器;最后以3枚導彈組成的楔形編隊為例進行了仿真，表明了該控制方法能夠在領彈機動的前提下，在避障過程中實現對跟隨彈的速度、彈道偏角和彈道傾角的控制，以完成對導彈編隊隊形的變換，具有較強的魯棒性和穩定性，且方法簡單，易于實現。

[1]Fidelis Adhika Pradipta Lie，Tiauw Hiong Go.A collisionfree formation reconfiguration control approach for unmanned aerial vehicles[C]//IEEE International Journal of Control，Automation and Systems，2010:1100 －1107.

[2]Naigang Cui，Changzhu Wei，Jifeng Guoea，et al.Study on missile formation reconfiguration optimized trajectory generation and control[J].Journal of Applied Mechanics，2010，77(5):1 －10.

[3]Sefer Kurnaz，Emre Eroglu，Okyay Kaynak，et al.A frugal fuzzy logic based approach for autonomous flight control of unmanned aerial vehicles[M].Springer，MICAI 2005:1155－1163.

[4]Mu Xiaomin，Du Yang，Liu Xing，et al.Behavior-based formation control of multi-missiles[C]//IEEE Control and Decision Conference，2009:5019－5023.

[5]Weitz L A，Hurtado J E.Decentralized cooperative control design for multivehicle formation[J].Journal of Guidance，Control，and Dynamics，2008，31(4):970 －979.

[6]劉小雄，章衛國，王振華，等.無人機自適應編隊飛行控制設計與仿真[J].系統仿真學報，2009，21(5):1420－1422.