單軸旋轉引起加速度計尺寸效應誤差分析及補償*

梁茂柱，王 超，杜鵬程

(1 91040部隊，山東青島 266100;2海軍潛艇學院，山東青島 266044;3 92196部隊，山東青島 266000)

0 引言

單軸旋轉慣導系統通過旋轉機構周期性旋轉能夠補償慣性元件常值漂移在轉軸垂直方向上分量以及部分安裝誤差[1]，在系統中引入阻尼，可以消除系統的舒拉周期和傅科周期振蕩誤差，同時抑制隨機漂移的影響，提高系統的精度。

在系統轉臺旋轉時，會產生加速度計尺寸誤差效應[2]，相當于加速度計的常值漂移，雖然在長時間導航過程中，通過旋轉能夠使由尺寸效應誤差產生的導航位置誤差相互抵消，不會累積[3]，但加速度計尺寸效應誤差會增加系統速度誤差的振蕩幅值，降低系統的速度精度;此外，對水平阻尼單軸旋轉慣導而言，由加速度計尺寸效應產生的加速度相當于載體的偽加速信號，這個信號將對不滿足舒拉調諧條件的阻尼系統產生較大的動態誤差。文中重點對由單軸旋轉運動引起的加速度計尺寸效應誤差及其影響進行分析，并給出了補償方法。

1 單軸旋轉引起的加速度計尺寸效應誤差分析

慣導系統通常采用3個一組的加速計測量沿3個正交軸方向的運動，得到作用在載體上的比力。在理想情況下，3個加速度計需要準確安裝在載體的同一位置，顯然，這是不可能實現的，因為加速度計有一定的尺寸，并且慣導系統的硬件安裝位置也受到限制，由于加速度計相對于理想位置存在物理偏差，其敏感到的切向力和向心力被稱作加速度計的尺寸效應[2]。

只要安裝在載體上的慣導系統的加速度計組件姿態相對慣性坐標系發生變化，由于尺寸效應，加速度計就會產生測量誤差，這種誤差與加速度計的缺陷無關，即使慣性導航系統采用沒有任何誤差的加速度計，仍然存在尺寸效應誤差。文中不考慮由于載體機動以及海浪等因素導致載體姿態發生變化而產生的尺寸效應誤差，考慮地球自轉，分析單軸旋轉引起的加速度計的尺寸效應誤差。

如圖1所示，OENU為當地地理坐標系(導航坐標系)，Oxryrzr為旋轉坐標系，初始時刻，旋轉坐標系Oxryrzr與OENU重合，坐標系Oxryrzr繞OU軸以角頻率ωr單向旋轉，3個加速度計分別放在旋轉坐標系Oxryrzr的坐標軸上，距離理想點O的距離為l。地球自轉角頻率為ωie，當地地理緯度為φ，t時刻Oxryrzr坐標系轉過ωrt角度，令繞Oxr軸、Oyr軸和Ozr軸的角頻率分別ωxr，ωyr和 ωzr，則:

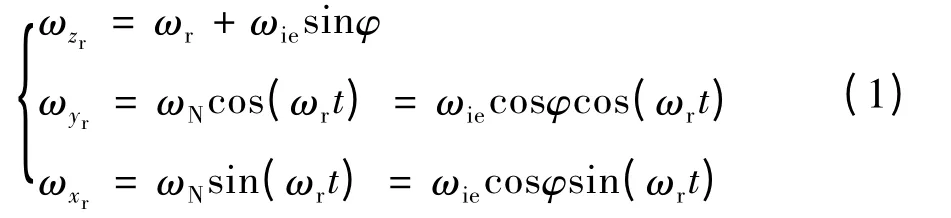
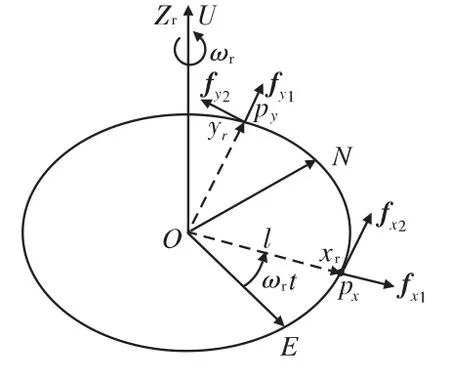
圖1 速度計組件坐標系相對導航坐標系變化示意圖

則Oxr、Oyr軸上px、py點受到的絕對加速度分別為:

式中:fx1、fy1分別為 px、py點的離心加速度，fx2、fy2分別為px、py點的切向加速度，其中:

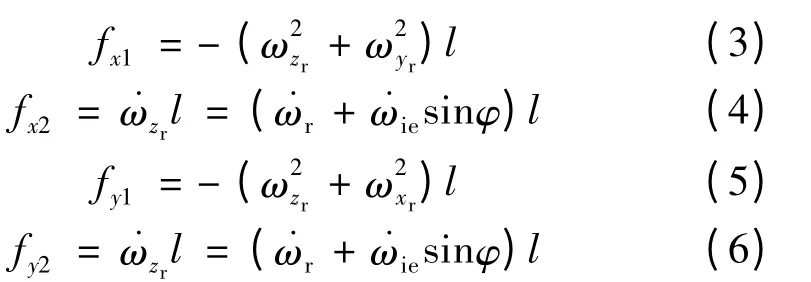
由于ωr和ωie為定值，所以fx2=fy2=0，可以忽略加速度計的測量值中的切向力，將式(1)代入式(2)，由于 ωie? ωr，化簡得 Oxr、Oyr軸加速計測得比力的大小分別為:

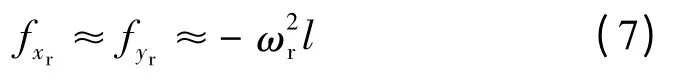
將加速度計尺寸效應誤差轉換到導航坐標系下，得到載體等效東向和北向偽加速度分別為:

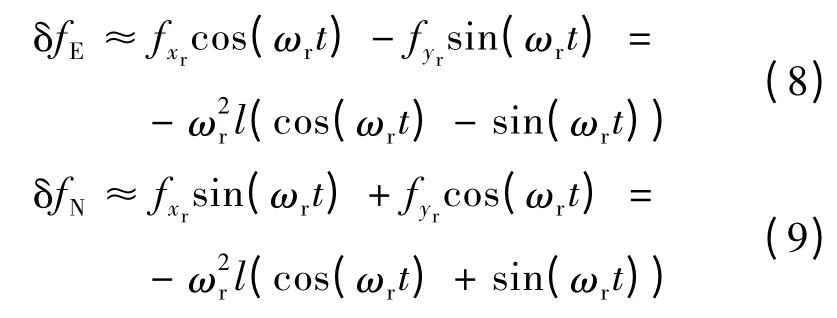
由式(8)和式(9)可知，在旋轉過程中，加速計尺寸效應誤差將引起載體的偽加速度，這個偽加速度呈現周期性振蕩形式，載體東向和北向偽加速度的最大值為，該偽加速度將增加系統速度的振蕩幅值，影響慣導系統輸出的速度和姿態精度;在一個旋轉周期內，分別對式(8)和式(9)進行積分，積分值為零，可見，在長時間的導航過程中，單軸旋轉使由加速度計尺寸效應誤差引起的誤差相互抵消，不會引起誤差的發散。

以系統導航計算平臺北向通道為例，說明等效北向加速度誤差對系統速度誤差影響，如圖2所示。

在無阻尼條件下，北向加速度誤差δfN(s)到系統速度誤差δVN(s)的傳遞函數為:

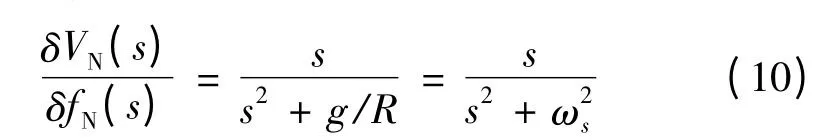
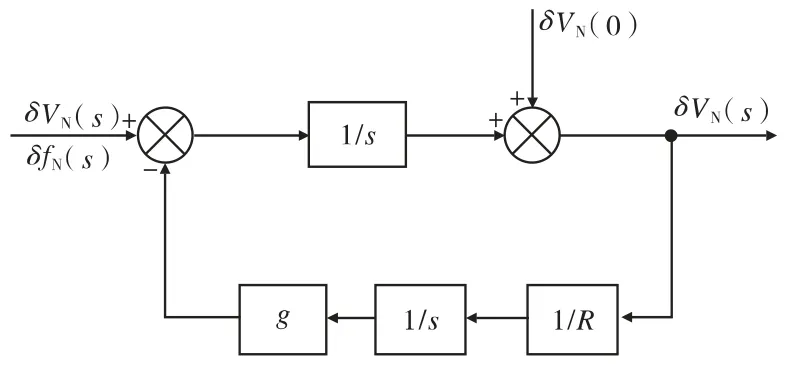
圖2 無阻尼單軸旋轉慣導北向通道方塊圖

由式(8)得:

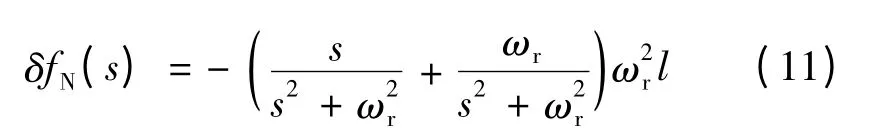
將式(11)代入式(10)得:

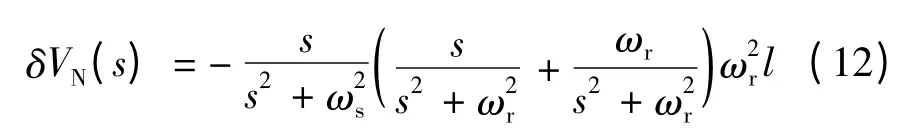
對式(12)兩邊取拉普拉斯反變換，得到北向速度誤差的時域表達式:

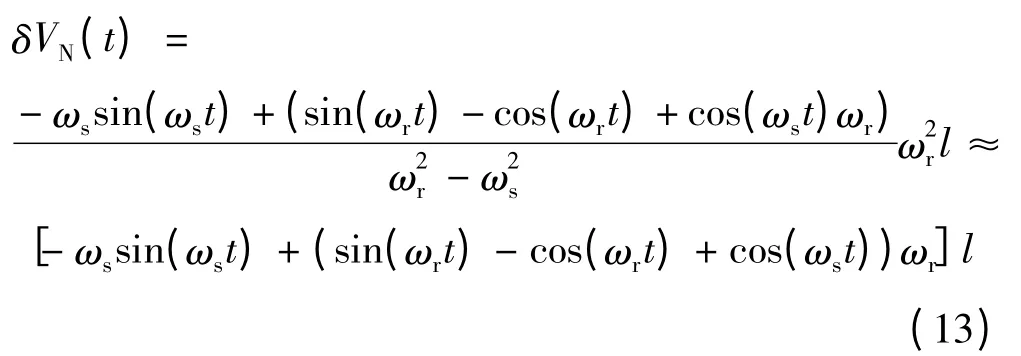
由式(7)和式(13)可知，由旋轉引起的加速度計尺寸效應誤差可以等效為加速度計的常值漂移，與和l成正比;由加速度計尺寸效應誤差引起的速度誤差與ωr和l有關，速度誤差的極值隨著ωr的增大而增大。當 ωr=18°/s，l=0.1m 時，引起的加速度計常值漂移約為0.0098696m/s2，引起的速度誤差的極值約為 0.14kn。

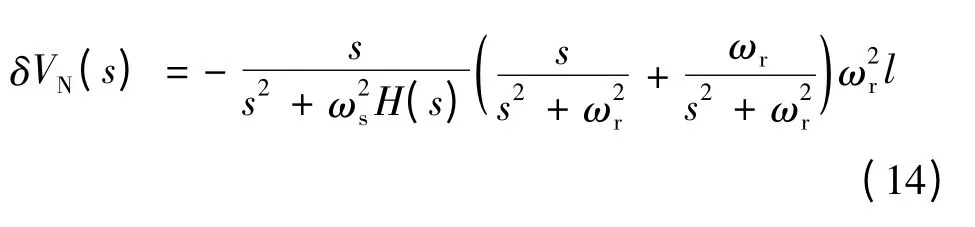
在水平阻尼條件下，由旋轉運動引起的速度誤差的頻域表達式為:H(s)為加入的校正網絡[4]。在系統中加入校正網絡，系統變成阻尼系統，將不滿足舒拉調諧條件，在等效北向偽加速度的作用下將產生動態誤差。由于在水平阻尼條件，求解北向速度誤差δVN(t)的時域表達式較為復雜，不便分析，后面將通過計算機仿真的方法，分析加速度計尺寸效應誤差引起的速度誤差。

2 加速度計尺寸效應誤差的補償

通過以上分析可知，加速度計尺寸效應誤差跟旋轉機構的轉速有關，為降低尺寸效應引起的誤差，可以在進行旋轉方案設計時采用較低的旋轉速度降低尺寸效應誤差，但這會影響對其它誤差的補償效果[5]。由式(7)可知，在旋轉過程中，根據旋轉機構的轉速可估計產生的加速度計尺寸效應誤差，把估計的誤差補償到加速度計的測量值中，再將補償后的加速度信息送入導航計算機進行導航解算，即可實現對加速度計尺寸效應誤差的補償，此方法簡單易于實現，其補償原理如下式所示:

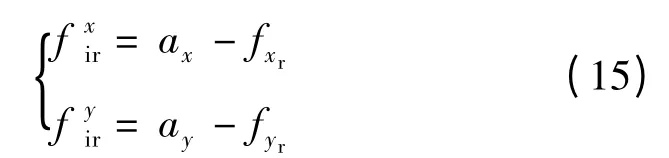
其中:ax、ay分別為兩個水平加速度計測得的比力，fxr、fyr為由于旋轉引起的加速度計尺寸效應誤差、為補償后的比力。經過補償后，將大大降低加速度計測量值中的尺寸效應誤差，減小由尺寸效應誤差引起的系統水平速度誤差和姿態角誤差。

3 仿真分析

采用單軸正反轉停方案[6]，旋轉周期為20min，旋轉時間為2min，停 止 時間為 18min，加速度計敏感中心到理想位置點的距離為0.1m，緯度為36°，只考慮單軸旋轉慣導系統中的加速度計尺寸效應誤差。采用時間步距仿真技術，分析加速度計尺寸效應誤差對系統精度的影響，并驗證對加速度計尺寸效應誤差補償的效果。仿真結果分別如圖3和圖4所示。A表示在水平阻尼工作狀態下，沒有補償加速度計尺寸效應誤差系統輸出的位置誤差曲線;B表示在無阻尼工作狀態下，沒有補償加速度計尺寸效應誤差系統輸出的位置誤差曲線;C表示在水平阻尼工作狀態下，補償加速度計尺寸效應誤差后系統輸出的位置誤差曲線。

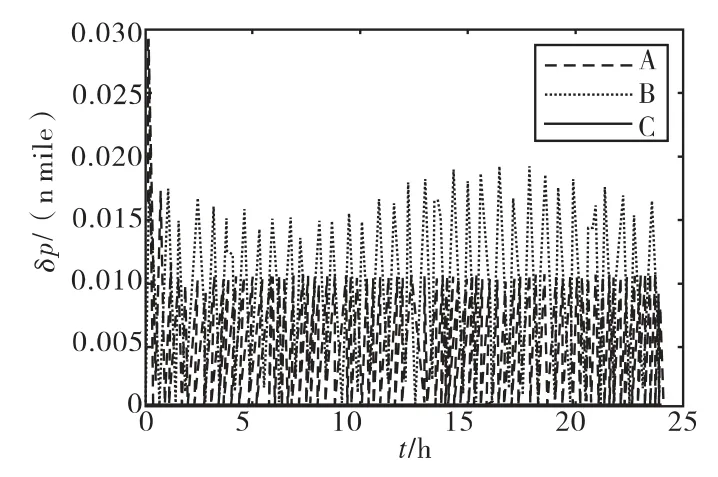
圖3 位置誤差曲線

從圖3中可以看出，在無阻尼條件下，加速度計尺寸效應誤差將引起系統位置誤差的振蕩，但不會引起系統位置誤差的發散，最大位置誤差約為0.02n mile;在水平阻尼條件下，位置誤差發生以旋轉周期為周期的振蕩，最大誤差約為0.012n mile，對加速度計尺寸效應誤差進行補償后，系統的位置誤差非常小，可以忽略不計。

從圖4中可以看出，在無阻尼條件下，加速度計尺寸效應誤差將引起系統速度誤差的振蕩，振蕩誤差的最大值約為0.14kn，與前面理論分析一致;在水平阻尼條件下，系統受到偽加速信號的影響，將產生動態誤差，最大誤差約為0.15kn，補償加速度計尺寸效應誤差后，系統輸出速度誤差約為0，可以忽略不計。

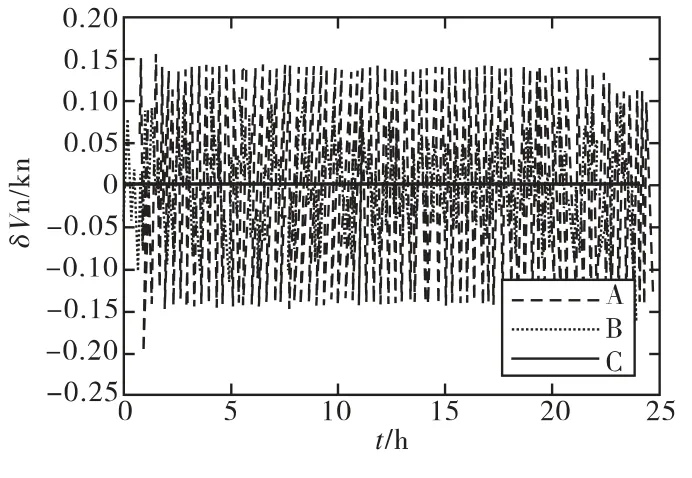
圖4 北向速度誤差曲線

4 結論

單軸旋轉慣導系統在旋轉過程中，會增大加速度計的尺寸效應誤差，相當于加速度計的常值漂移，將誤差變換到導航坐標下，相當于測得的載體偽加速信號。在長時間導航過程中，由于旋轉可以實現誤差的相互抵消，不會引起系統導航定位誤差的發散。然而，在系統旋轉過程中，這個加速度將增加無阻尼系統姿態角誤差和水平速度誤差的振蕩幅值;對水平阻尼單軸旋轉慣導而言，由于不滿足舒拉調諧條件，受到偽加速信號的影響，將產生較大的動態誤差，嚴重影響系統輸出的水平速度和姿態角精度。通過補償由旋轉導致的加速度計尺寸效應誤差，可有效降低系統的振蕩誤差，提高系統在旋轉過程中輸出的速度、姿態精度。

[1]袁保倫，饒谷音.光學陀螺旋轉慣導系統原理探討[J].國防科技大學學報，2007，28(6):76－80.

[2]David H Titterton，John L Weston.捷聯慣性導航技術[M].張天光，王秀萍，王麗娜，等，譯.北京:國防工業出版社，2007.

[3]袁保倫.四頻激光陀螺旋轉式慣導系統研究[D].長沙:國防科技大學，2007.

[4]陳永冰，鐘斌.慣性導航原理[M].北京:國防工業出版社，2007.

[5]于旭東，王宇，張鵬飛，等.單軸旋轉對慣導系統誤差特性的影響[J].中國慣性技術學報，2008，16(6):643－648.

[6]海娜，陸全聰，黃昆，等.旋轉式光學陀螺捷聯慣導系統的旋轉方案設計[J].中國慣性技術學報，2009，17(1):8－14.